Алгоритм может быть сформулирован в процессе изучения материала и служит базой для рассуждений при выполнении заданий данного типа.

Составим и решим уравнение, заданное в условиях, отличных от прежних. Сформулируем алгоритм нахождения корня уравнения, основанный на способе графического моделирования.

Предложим вспомогательные и математические модели уравнений с использованием числового отрезка.

Для обсуждения способа нахождения корня уравнения предложим систему вопросов:

- С какого числа записано уравнение? Почему?

- Когда в уравнении ставят знак «–», а когда «+»?

- Какое число записывают после знака «=»? Почему?

- Как найти корень уравнения, опираясь на числовой отрезок?

Осуществим план составления уравнения и нахождения его корня.

· Алгоритм решения уравнения с помощью числового отрезка

· Запишу число, от которого направлена стрелка.

· Поставлю знак арифметического действия (если направление движения влево – «–», вправо – «+»).

· Обозначу неизвестный компонент буквой х.

· Запишу знак равенства и число, на котором завершено движение стрелки.

· Посчитаю, сколько единиц между числами.

· Запишу ответ.

 

Алгоритм решения уравнений на основе взаимосвязи между частями и целым

4.   Как сформировать умение младших школьников составлять  алгоритмические предписания? Приведите примеры различных упражнений с этой целью.

Понятие алгоритма возникло в математике, применяется оно и в кибернетике, и ряде других наук, включая психологию и педагогику.

В теорию и практику обучения понятие алгоритма вошло в конце 50-х годов в связи с развитием программированного обучения и применением обучающих машин.

«Алгоритм - одно из важнейших понятий информатики, точное, однозначно понимаемое предписание о выполнении в указанной последовательности операций (действий), приводящих к решению любой из задач, принадлежащих к некоторому классу или типу. Предписываемые операции (действия) должны быть доступны адресату. Они могут быть как элементарными (простейшими), так и сложными, основанными на элементарных».

Математика и логика при построении теории алгоритмов полностью отвлекаются от человеческого фактора, а психология и педагогика именно его изучают и им управляют. Устройством, осуществляющим алгоритмические процессы, является человек. В педагогике и психологии используется некоторая модификация понятия алгоритма. Л.Н. Ланда, специально занимавшийся разработкой алгоритмических методов в обучении, дал им название: «предписание алгоритмического типа», или «алгоритмическое предписание».

Предписания алгоритмического типа или алгоритмические предписания - это алгоритмы, которые предназначены специально для человека и которые учитывают особенности его психики и организма. Алгоритм - это уже предписание, указывающее последовательность действий, которые приводят к решению любой задачи. Поэтому с названием «алгоритмическое предписание», данным ученым Л.Н. Ландой, мы согласны, но для простоты пользования понятием в работе с учащимися мы будем апеллировать к слову «алгоритм».

Для формирования алгоритмического мышления нужно научить детей: находить общий способ действия; выделять основные, элементарные действия, из которых состоит данное; планировать последовательность выделенных действий; правильно записывать алгоритм.

Составление алгоритмических предписаний – сложная задача, поэтому начальный курс математики не ставит своей целью её решение. Но определённую подготовку к её достижению он может и должен взять на себя, способствуя тем самым развитию логического и алгоритмического мышления школьников.

При формировании алгоритмических понятий выделяют 3 понятия:

1.Введение алгоритма:

а) актуализация знаний;

б) открытие алгоритма учащимися под руководством учителя;

в) формула алгоритма;

2.Усвоение: а) отработка отдельных операций, входящих в алгоритм и усвоение их последовательности;

3.Применение алгоритма: а) отработка алгоритма в знакомой и незнакомой ситуациях;

Обучение алгоритму можно производить по-разному: можно давать в готовом виде, чтобы их заучить, а затем закрепить во время упражнений. Но можно и «открывать» алгоритм самими учащимися. Этот способ требует большего времени, но очень ценен.

В целях оперативного контроля за усвоением алгоритма в программы могут вводиться специальные типы тетрадей для самостоятельных и проверочных работ. Задания могут быть такого вида что, выполняя их, ученик должен расчленить процесс решения на отдельные операции, а затем с необходимостью все их производить, ясно и чётко осознавая каждую из них. Ученик не может уклониться от выполнения необходимых работ, т.к. он должен фиксировать в тетради результаты каждой операции. Благодаря таким тетрадям учитель осуществляет контроль прямо на уроке.

Основными свойствами алгоритма являются:

1) определённость (простота и однозначность операций);

2) массовость (целый класс задач);

3) результативность (обязательное подведение к ответу);

4) дискретность (членение на отдельные элементарные шажки);

Например, в 1 классе уже на этапе подготовки к решению задач (составление рассказа по рисункам), учитель знакомит детей с алгоритмом:

- что будем находить: целое или часть;

- что известно;

- какое действие выбрать;

- составление числового выражения;

С этого процесса начинается обучение решению текстовых задач. Умение решать такие задачи - фундамент, на котором строится работа с более сложным материалом. Работа с текстовыми задачами является важным и весьма трудным разделом математики. И процесс этот многоэтапен: он включает в себя перевод словесного текста на язык математический (построение математической модели), решение и анализ полученных результатов. Краткая запись условия задачи - примеры моделей. Метод математических моделей позволяет сформировать у учащихся навыки алгоритмического мышления и научить их: а) анализу; б) установлению взаимосвязей между объектами задачи, построению схемы решения; в) интерпретации полученных решений для исходной задачи; г) составлению задач по готовым моделям. Без применения моделей и моделирования невозможно эффективно изучать различные объекты в сферах деятельности человека, а правильное и чёткое выполнение определённой последовательности действий требует от специалистов многих профессий владение навыками алгоритмического мышления. И многое теряют те учителя, которые не обращают особого внимания на краткую запись условия задачи, считая, что ребёнок и так справится с решением задачи, забывая о том, что пропускают наиболее важный момент для формирования алгоритмизации мышления младших школьников.

В курсе математики алгоритмы представлены в виде арифметических правил, последовательности действий. Вот какие это действия, например, при решении сложных неравенств в 1 классе, при сравнении их (5+4…6+4):

- находим значение левой части неравенства;

- находим значение правой части неравенства;

- сравниваем;

- ставим знак;

- делаем выводы;

И, конечно же, учитель вправе спросить, а можно ли не подсчитывать значения частей. Дети с развитым логическим мышлением обязательно ответят утвердительно и докажут, что в левой части первое слагаемое – 5, а в правой – 6.Число 5 стоит левее на числовом отрезке, чем 6. Значит, правая часть больше левой, а левая меньше правой.

Обучение школьников умению «видеть» алгоритмы и осознавать алгоритмическую сущность тех действий, которые они выполняют, начинается с простейших алгоритмов, доступных и понятных им. Например, алгоритм пользования бытовыми приборами, приготовление различных блюд, переход улицы, покупка товаров в магазинах самообслуживания. В учебнике информатики 4 класса, например, изучается и записывается алгоритм съедения банана. А вот как выглядит алгоритм письменного деления многозначных чисел на одно – и двузначное число:

- определи количество цифр в частном;

- найди первое неполное делимое;

- раздели на делитель;

- найди остаток;

- сравни остаток с делителем;

- найди 2, 3 неполные делимые и т.д.;

- закончи деление до конца.

Работая по алгоритмическим шажкам, ребёнок делит без ошибок, т.к. он помнит о первом шажке алгоритма и никогда не пропустит тот же ноль. Да и вообще, учитель должен всегда помнить, что самое важное при обучении устным и письменным приёмам вычислений отводится алгоритмизации.

Например, такое задание: «Запиши числа от 1 до 6.Каждое увеличь: а) на 2; б) на 3» можно представить в такой таблице:

Таким образом, алгоритмические предписания можно задавать словесным способом, схемой и таблицей. Действуя с конкретными математическими объектами и обобщениями в виде правил, дети овладевают умением выделять элементарные шаги своих действий и определять их последовательность.

Например, правило проверки сложения можно сформулировать в виде алгоритмического предписания так:

1.Из суммы вычесть одно из слагаемых;

2.Сравнить полученный результат с другим слагаемым;

3.Если полученный результат равен другому слагаемому, то сложение выполнено правильно;

4.В противном случае ищи ошибку.

Задания

1 вид: задания на выделение признаков у одного или нескольких объектов. Их цель - обратить внимание ученика на значимость того или иного признака объекта для выполнения задания. Предлагаются задания на опознания этого признака, на группировку объектов по выбранному признаку (цвет, размер, форма и т. п.) при этом задание оформлено в виде инструктивного письма графической формы, понятной ребенку без текста, что позволяет использовать эти материалы даже при работе с детьми, не умеющими хорошо читать.

Пример. Раскрась картинку по заданию

В следующем задании первокласснику предлагается выполнить замену фигур по инструктивному письму и нарисовать ту же картинку заново. Кроме замены фигур, нужно произвести замену цвета по заданию. При этом ученик самостоятельно решет проблему альтернативного выбора «или»:

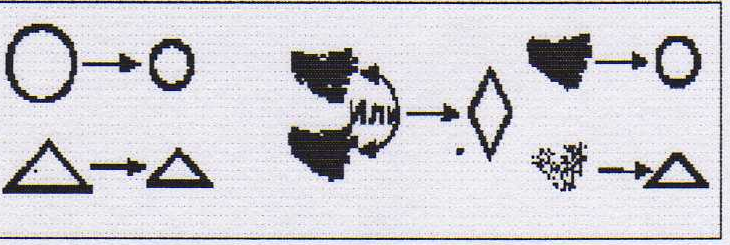
Задание. Определи, что меняет робот. Нарисуй фигуры и раскрась, используя трафареты так, как их меняет робот:

2 вид: задания на прямое распределение признаков. На первых порах эти задания оформлены в виде логических деревьев, так как это помогает в наглядной форме представить ребенку само действие распределения. Признаки распределения: цвет, форма, размер.

Задание. Помоги фигуркам найти свой дом.

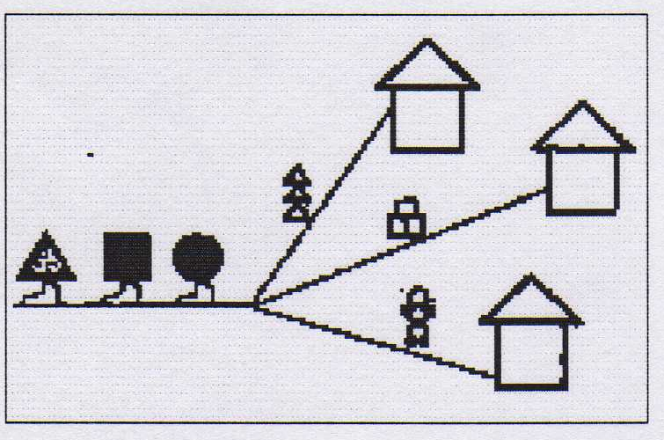
3 вид: задания на распределение с использованием отрицания одного из признаков.

Пример. Раскрась мышек по заданию:

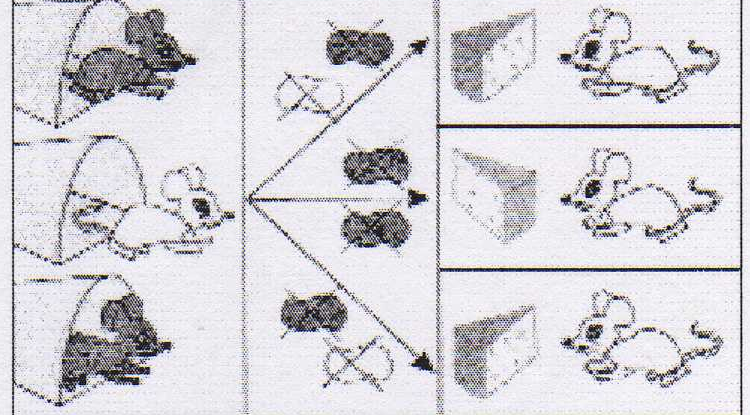
4 вид: задания, связанные с изменением признака. Графически эти задания оформлены в виде «волшебных ворот», проходя через которые предмет изменяет один из указанных признаков. Важно, чтобы ученик понял, что изменение избирательное, то есть изменяется только указанный признак. Эти задания полезны не только для развития восприятия, внимания и памяти, но и для развития внутреннего плана действий и развития гибкости мышления. В дальнейшем это умение поможет школьнику лучше понимать функциональные зависимости, зависимости изменения одних элементов математических объектов (математических выражений, задач, уравнений) от изменений других элементов. Наиболее сложные в этой группе – задания на двойное изменение признака.

Пример. Замени форму вагонов по заданию и нарисуй поезд после прохода через волшебные ворота.

Задания (двойное изменение признака):

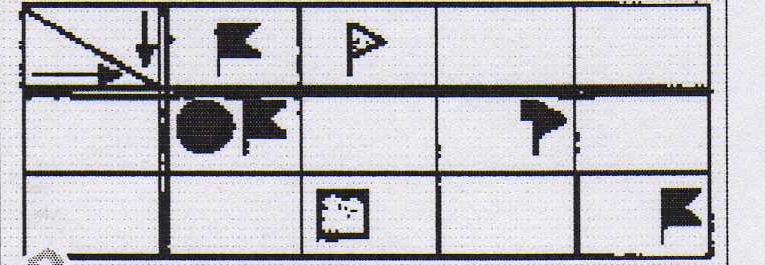
а) Подумай, как изменится цвет флажков после прохода через волшебные ворота.

б) подумай, как изменится цвет флажков после прохода через первые волшебные ворота. Как изменятся флажки после прохода через вторые ворота? Нарисуй их.

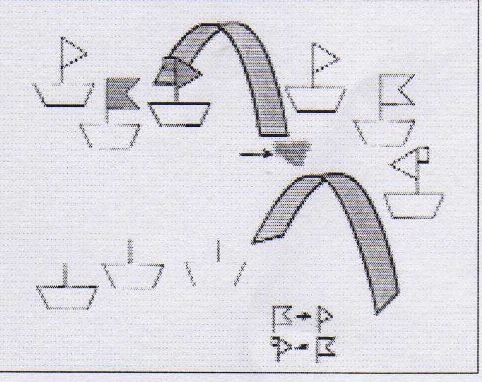
Задание на изменении признака может быть также сформулировано в виде инструктивного письма.

Пример. Раскрась цветы в вазах по заданию:

5 вид представляет те же виды заданий, но трансформированные в другую графическую форму – матрицы (прямоугольные таблицы). Этот графический вид более формализованный. Чем предыдущий, но он широко используется в различных областях (математика, информатика и др.). Фактически простейшие матрицы – это то же самое распределение признаков, однако иная графическая форма (лишенная элементов движения, а значит, и жизненной реальности, от которой весьма зависит ребенок этого возраста, мыслящий конкретно) менее понятна ученику 6-7 лет и требует постепенной адаптации. Целесообразно сначала предложить ему задание на матрице с использованием уже знакомого «инструктивного письма».

Задание. Выполни замену и заполни пустые клетки.

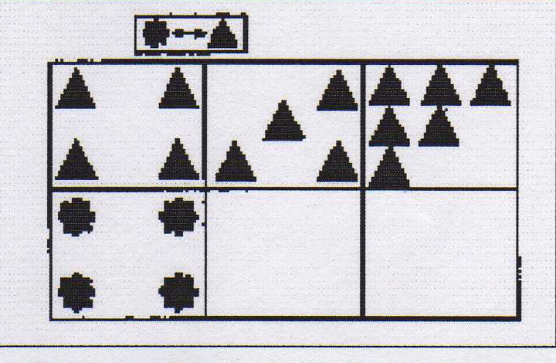
Задание. Подумай, по какому принципу меняется порядок фигур. Заполни третий и четвертый ряды по тому же принципу.

Раскрась фигуры, соблюдая порядок.

6 вид: задания на поиск недостающей фигуры, также оформленные в виде неполной матрицы (таблицы). Умение справляться с заданиями такого вида традиционно считается показателем высокого уровня умственного развития.. анализ формы представления такого задания показывает, что от традиционной (полной) матрицы оно отличается отсутствием задающих строк и стобцов. Иными словами, если в традиционной таблице требуется по заданным строкам и столбцам («причина»), используя принцип сочетания признаков, заполнить пустые клетки («следствие»), то в таблице на поиск недостающего элемента заполнение пустой клетки («следствие») требует восстановления опущенных задающих строк и столбцов («причина»), а затем определения на этой основе недостающей фигуры. В таком «конечном» виде эти задания достаточно трудны. Однако методически очевидно, что возможно и целесообразно выстроить систему подготовки к этим заданиям, и тогда ребенок сможет самостоятельно справляться с достаточно сложными вариантами (сформируется самостоятельное интеллектуальное умение).

Задание. Подумай, что нарисовать в пустом окошке, чтобы сохранить тот же принцип. Раскрась фигурки по заданию.

Задание. Заполни пустые клетки, соблюдая тот же принцип.

Задание. Заполни пустые клетки по заданному принципу.

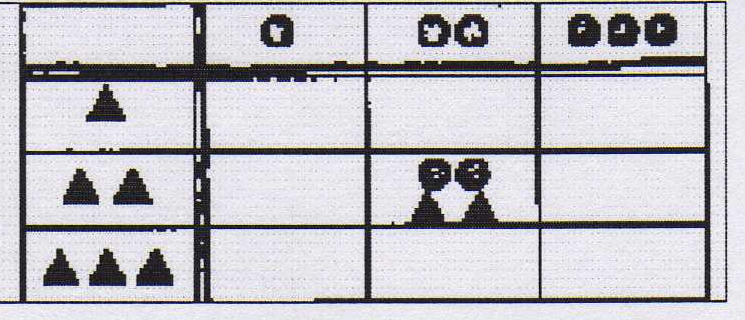
Задание. Подумай, что может стоять в пустых клетках.

7 вид представляет те же виды заданий, но трансформированные в новую графическую форму – алгоритмическую схему. Цель таких заданий – научить ребенка читать и понимать схематическую запись алгоритма. Линейные алгоритмы традиционно используются на уроках математики в начальной школе: на устном счете учитель приводит цепочки вычислений. Оформление такой цепочки приближает ее к классической записи алгоритма. Следует отметить, что классическая форма записи алгоритма достаточно формализована и привыкание к ней ребенка является довольно длительным процессом. Однако сама эта форма вызывает у детей интерес и позволяет достаточно быстро вводить в работу как разветвляющийся алгоритм, так и цикличный.

Задание. Вычисли по схеме.

Задание. Вычисли по схеме два варианта результата

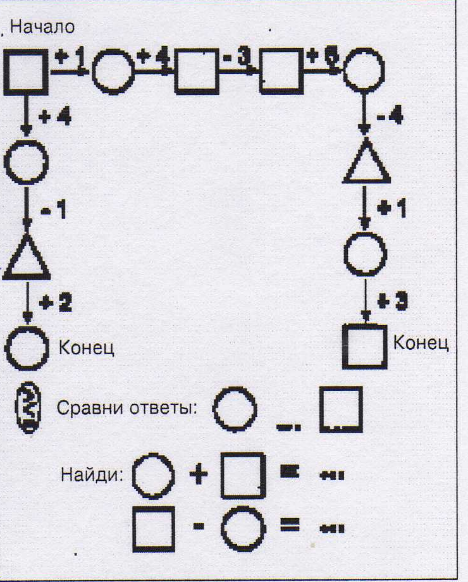
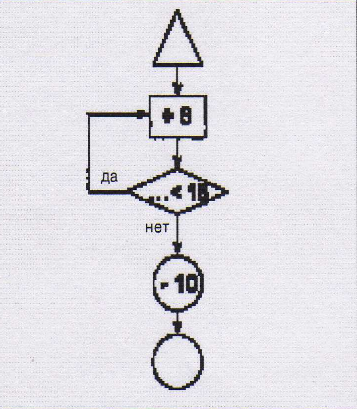
Задание. Вычисли по схеме, подставив любое число, меньшее, чем 10.

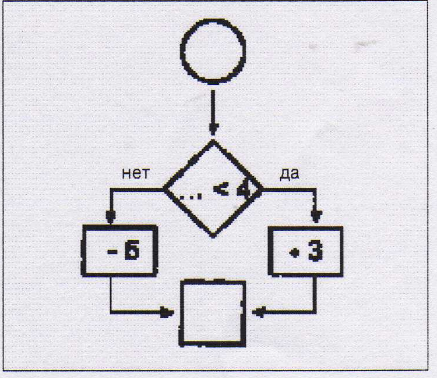
Задание. Вычисли по схеме.

Особое внимание в системе заданий уделено развитию словесно-логического мышления: пониманию специальных речевых структур с употреблением связок «и», «или», «тоже», «только», и слов «все», «некоторые», «любые».

Задание.

а) Раскрась красным цветом все треугольники.

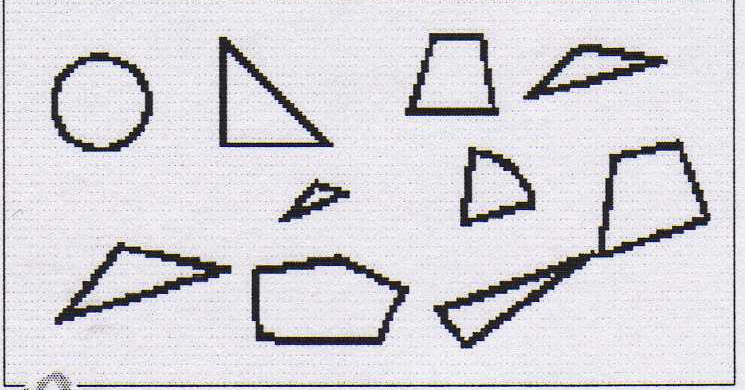
б) некоторые фигуры на рисунке задания а) являются четырехугольниками. Раскрась их зеленым цветом.

В ) Только одна фигура на рисунке задания а) – это круг. Раскрась его синим цветом.

Г) Сравни человечков и закончи высказывание:

Все…

Только один…

Задание.

А) Даны числа:

5, 18, 13, 24, 74, 81, 90, 44, 21, 4.

Обведи красным карандашом числа, в записи которых одна цифра или есть цифра 4.

Б) Даны числа:

71, 3, 17, 59, 58, 19, 2.

Обведи зеленым цветом числа, в записи которых две цифры и есть цифра 7.

Задание. Робот думает: помоги ему выбрать фигуру и нарисуй ее.

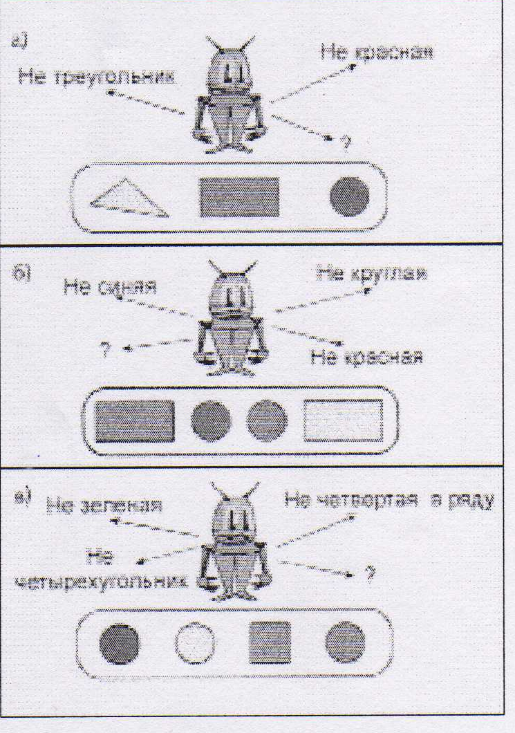
Задание. Зачеркни лишнее слово и закончи высказывание.

А) Помидор, огурец, стакан, картофель, лук.

Все оставшиеся слова обозначают…

Б) Нитки, иголки, ножницы, бумага, катушки.

Все остальные слова обозначают…

В) Дед, бабка, внучка, Жучка, кошка, домовой, мышка.

Все оставшиеся слова обозначают…

Г) Курица, индюшка, аист, гусь, утка.

Все оставшиеся слова обозначают…

Д) молоко, сок, вода, шампунь, квас, лимонад.

Все оставшиеся слова обозначают…

Е) корова, овца, свинья, волк, кошка, собака.

Все остальные оставшиеся слова обозначают…

Ж) Стол, кастрюля, стул, диван, кресло, тумбочка.

Все оставшиеся слова обозначают…

Задание. Отметь верные высказывания.

А) Существуют числа, сумма которых больше 5.

Не существует чисел, сумма которых больше 5.

Б) Существуют треугольники, из которых можно сложить квадрат.

Не существует треугольников, из которых можно сложить квадрат.

В) некоторые числа можно записать двумя одинаковыми числами.

Все числа нужно записывать разными цифрами.

Охарактеризуем методику работы с заданиями.

Чтобы максимально стимулировать индивидуальные способности младшего школьника и обеспечить его дальнейшее развитие, не дается никаких предварительных инструкций типа «раскрасьте в указанный на веточке цвет». Это лишает ребенка возможности самостоятельно догадаться, выявить признак, закономерность и т.п. Полезно сначала предложить ученику самому определить смысл задания, не читая его текст. Графического оформления задания достаточно, чтобы при определенно умственном усилии ребенок сам мог сообразить, что нужно сделать. Это позволяет активно влиять на развитие сильного самостоятельного типа мышления, логической интуиции и самоконтроля у ребенка. Текст задания предназначен, скорее, учителю, чтобы в случае необходимости оказать ученику дозированную помощь (т.е. минимальную помощь, которая позволит ребенку дальше двигаться самостоятельно).

Инструктаж при выполнении задания может быть таким:

1. помогите разложить конфеты (грибы, мячи и т. п.) правильно.

2. Попробуйте догадаться. Какой вариант будет правильным. Правило зашифровано в рисунке (в рамочке рядом с рисунком, если это инструктивное письмо).

3. Кто считает, что он догадался верно? Почему? Кто может объяснить? Кто не согласен? Почему?

4. Учитель подтверждает верный вариант (читает задание).

5. Дети выполняют задание.

Пункты 3,4 и 5 могут быть выполнены в другой последовательности: сначала дети выполняют задание так, как они его понимают (пункт 5 после пункта 2), а потом объясняют свой путь рассуждений (пункты 3 и4 после пункта 5). Этот путь более всего способствует развитию самостоятельности мышления, самоконтроля и логической интуиции. Очевидно, что такой методический подход способствует также развитию математической речи школьника.

5. Опишите методику обучения младших школьников решению комбинаторных задач. Какие способы решения комбинаторных задач вам известны из курса математики? Какими способами решения этих задач могут воспользоваться учащиеся начальных классов? Приведите примеры.

(По статьям Белокуровой Е.Е. и др.)

Комбинаторика возникла в XVI веке и первоначально в ней рассматривались комбинаторные задачи, связанные в основном с азартными играми. В процессе изучения таких задач были выработаны некоторые общие подходы к их решению, получены формулы для подсчета числа различных комбинаций.

В настоящее время комбинаторика является одним из важных разделов математической науки. Ее методы широко используются для решения практических и теоретических задач. Установлены связи комбинаторики с другими разделами математики.

В начальном обучении математике роль комбинаторных задач постоянно возрастает, поскольку в них заложены большие возможности не только для развития мышления учащихся, но и для подготовки учащихся к решению проблем, возникающих в повседневной жизни.

Комбинаторные задачи в начальном курсе математики решаются, как правило, методом перебора. Для облегчения этого процесса нередко используются таблицы и графы. В связи с этим учителю необходимы определенные умения и навыки решения комбинаторных задач.

Комбинаторика - раздел математики, в котором изучаются вопросы о том, сколько различных комбинаций, подчиненных тем или иным условиям, можно составить из заданных объектов.

Комбинаторику можно рассматривать как введение в теорию вероятностей, поскольку методы комбинаторики используются для решения многих вероятностных задач, в которых речь идет о подсчете числа возможных исходов и числа благоприятных исходов в различных конкретных случаях.

Выбором объектов и расположением их в том или ином порядке приходится заниматься чуть ли не во всех областях человеческой деятельности.

С аналогичными задачами, получившими название комбинаторных, люди сталкивались в глубокой древности. Уже несколько тысячелетий назад в Древнем Китае увлеклись составлением магических квадратов, в которых заданные числа располагались так, что их сумма по всем горизонталям, вертикалям и главным диагоналям была одной и той же. В Древней Греции подсчитывали число различных комбинаций длинных и коротких слов в стихотворных размерах, занимались теорией фигурных чисел, изучали фигуры, которые можно составить из частей особым образом разрезанного квадрата и т.д.

Комбинаторные задачи возникли и в связи с такими играми, как шашки, шахматы, домино, карты, кости и т.д.

Путь освоения способов решения комбинаторных задач состоит из нескольких этапов: сначала решаются методом перебора и для записи используются различные способы, затем появляются правила суммы и произведения и дальше рассматриваются некоторые виды комбинаций, а их число подсчитывается по формулам.

Правило суммы: нахождение числа элементов объединения двух непересекающихся конечных множеств. Если объект а можно выбрать m способами, а объект b - k способами (не такими как a), то выбор «либо а, либо b» можно осуществить m+k способами.

Например: на тарелке лежат 5 яблок и 4 апельсина. Сколькими способами можно выбрать один плод.

Правило произведения: нахождение числа элементов декартова произведения. Если объект a можно выбратьm - способами, а объект b - k способами, то пару (a, b) можно выбрать m * k способами.

Например: 1. На тарелке лежат 5 яблок и 4 апельсина. Сколькими способами можно выбрать пару плодов, состоящую из яблок и апельсина. 2. Сколько трёхзначных чисел можно составить используя три цифры 7, 4 и 5.

Правила суммы и произведения - это общие правила решения комбинаторных задач. Кроме них в комбинаторике пользуются формулами для подсчёта числа отдельных видов комбинаций. С теоретико-множественной точки зрения запись любого двузначного числа - это кортеж длины 2. Записывая различные двузначные числа с помощью трёх цифр мы образовываем различные кортежи длины 2 с повторяющимися элементами. В комбинаторике такие кортежи называют размещениями.

Проанализировав сравнительную таблицу, я могу сказать про программы следующее. По программе «Школа 2100» комбинаторные задачи предлагаются для изучения, начиная с конца первого класса, а со второго класса входят почти во все уроки. Задачи решаются в общем методом перебора. Решение с помощью таблицы и дерева возможностей предлагается на отдельном уроке во 2 классе, но далее упоминания про решение задач другими способами нет. С методом решения комбинаторной задачи с помощью графов учащиеся не знакомятся.

По программе «Гармония» задачи в учебнике даются только в первом классе, первом полугодии. Начиная со второго полугодия комбинаторные задачи исчезают из учебников, взамен предлагается тетради на печатной основе как дополнение к учебнику. Первый год решают только методом перебора: хаотичного и организованного. При знакомстве с решением с помощью таблицы учащиеся сами открывают принцип заполнения таблицы, и далее при решении задач заполняют таблицы сами. С третьего класса учатся решать задачи с помощью графа и дерева возможностей.

По программе «Школа России» задачи решаются только методом перебора и задач при этом не очень много. Предлагаются задания после некоторых тем вместе или по очереди с логическими заданиями. В 4-ом классе таких задач не было найдено.

Методика обучения решению комбинаторных задач разрабатывалась в рамках методической системы развивающего обучения младших школьников математике (Н.Б. Истомина), которая выражает необходимость целенаправленного и систематического формирования приемов умственной деятельности в процессе усвоения математического содержания.

Нацеленность начального курса математики на формирование приемов умственной деятельности позволяет установить внутреннюю связь между развивающими условиями обучения и способами их достижения, так как в процессе усвоения знаний, умений и навыков приемы умственной деятельности выполняют различные функции и их можно рассматривать:

1) как способ организации учебной деятельности школьников;

2) как способы познания, которые становятся достоянием ребенка, характеризуя его интеллектуальный потенциал и способности к усвоению знаний;

3) как способы включения в процесс познания различных психических функций: эмоций, воли, чувств, внимания; в результате интеллектуальная деятельность ребенка входит в различные соотношения с другими сторонами его личности, прежде всего с ее направленностью, мотивацией, интересами, уровнем притязаний, т.е. характеризуется возрастающей активностью личности в различных сферах ее деятельности.

Решение комбинаторных задач требует активного использования таких приемов умственной деятельности как анализ и синтез, сравнение, классификация, обобщение.

Способы решения комбинаторных задач, обычно делят на две группы: «формальные» и «неформальные». При «формальном» пути решения нужно определить характер выборки, выбрать соответствующую формулу или комбинаторное правило, подставить числа и вычислить результат. Результат - это количество возможных вариантов, сами же варианты в этом случае не образовываются. Основные комбинаторные правила: сложения, умножения.

Примером решения комбинаторных задач формальным способом служат следующие задачи:

Задача. 1. Сколько словарей надо иметь, чтобы можно было выполнять переводы непосредственно с любого из пяти языков на любой из этих пяти?

Решение. Число словарей совпадает с числом упорядоченных подмножеств, содержащих два элемента из пяти. Для такого перевода надо иметь 20 словарей.

Задача 1. У кассы кинотеатра стоят четверо ребят. У двух из них сторублевые купюры, у других двух – пятидесятирублевые. (Учитель вызывает 4 учеников к доске и дает им модели купюр). Билет в кино стоит 50 рублей. В начале продажи касса пуста. (Учитель вызывает «кассира» и дает ему «билеты»). Как должны расположиться ребята, чтобы никому не пришлось ждать сдачи?

Методические указания: для решения задачи целесообразно разыграть сценку, с помощью которой можно найти два возможных варианта решения:

1. 50 рублей, 100 рублей, 50 рублей, 100 рублей;

2. 50 рублей, 50 рублей, 100 рублей, 100 рублей.

Если ученики нашли варианты в том порядке, в котором они представлены в электронном варианте «Сборника…», то можно открывать в процессе нахождения. Если порядок вариантов не совпадает, следует только проверить по электронному варианту.

Задача 2. В парке 4 пруда. Было решено засыпать песком дорожки между ними так, чтобы можно было пройти от одного пруда к другому кратчайшим путем, т.е. не нужно было идти в обход. Покажите, какие дорожки будут сделаны.

Методические указания: учитель обсуждает с учениками возможные варианты, после чего ответы проверяются с помощью электронного варианта «Сборника…».

 

Задача 3. 4 парусника готовились к соревнованиям. У каждого был свой корабль. Судьи решили, что надо раскрасить паруса, чтобы парусники были видны издалека, и было ясно, кто из спортсменов идет впереди, кто запаздывает. Покажите, как по-разному раскрасили паруса, если было всего две краски?

Методические указания: после прочтения задачи учитель может повесить заготовленные заранее модели парусников на доску, чтобы учащимся было легче сориентироваться в ситуации.

Далее учитель обсуждает с учениками возможные варианты, после чего ответы проверяются с помощью электронного варианта «Сборника…».

Таким образом, на подготовительном этапе создается положительная мотивация и эмоциональная подготовка учащихся к дальнейшему решению комбинаторных задач.

 

На основном этапе учащиеся знакомятся с разными способами решения комбинаторных задач.

На данном этапе решаются задачи четырех видов:

· задачи, решаемые методом организованного перебора;

· задачи, решаемые с помощью таблиц;

· задачи, решаемые с помощью графов;

· задачи, решаемые с помощью дерева возможных вариантов.

 

Для начала мы предлагаем ознакомить учащихся с методом организованного перебора. При решении данных задач важно обучить детей выполнять перебор не хаотически, а соблюдая определенную последовательность перебора всех вариантов решений.

 

Задача 4. На каждом флажке должны быть полоски разного цвета: синяя, красная, белая. Раскрась флажки так, чтобы они отличались друг от друга. Сколько разных флажков ты раскрасил? Можете ли вы указать способ позволяющий назвать число флажков, не производя непосредственного их подсчёта?

Методические указания: Ответ на вопрос задачи предполагался после выполнения следующей работы. Этот же ответ предполагается и ответ на вопрос учителя.

Один цвет позволяет, очевидно, сделать один флажок (учитель открывает на слайде в электронном варианте «Сборника…» одну полоску, предупредив учащихся о том, что начинаем с красного цвета). Вторую цветную полоску можно приложить к этому флажку двумя способами при условии, что каждый цвет мы хотим использовать только один раз. Вторую полоску мы прикладываем сверху или снизу (также пользуясь электронным вариантом «Сборника…»):

Как можно добавить к этим цветным полоскам третью? Мы помещаем её либо сверху, либо снизу, либо посередине, между двумя первыми полосками. Так, из трёх разноцветных полосок можно составить всего 2*3=6 флажков.

 

Задача 5. Прямоугольник состоит из трех квадратов. Сколькими способами можно раскрасить эти квадраты тремя красками: красной, зеленой и синей?

Методические указания: при решении данной задачи можно предложить учащимся организовать перебор с помощью раскрашивания квадратов, предварительно установив порядок.

1. Пусть первый квадрат раскрашен красным цветом, тогда остальные квадраты можно раскрасить двумя способами: синим и зеленым, зеленым и синим.

2. Пусть первый квадрат раскрашен зеленым цветом, тогда остальные квадраты можно раскрасить двумя способами: красным и синим, синим и красным.

3. Пусть первый квадрат раскрашен синим цветом, тогда остальные квадраты можно раскрасить двумя способами: красным и зеленым, зеленым и красным. В результате получаем всего 6 способов.

При этом квадраты можно открывать постепенно на слайде электронного варианта «Сборника…», тем самым, контролируя ответы учеников.

Задача 20. Миша, Вася, Катя и Лиза поздравили друг друга с Новым годом, подписав открытки. Покажи красным цветом стрелки, которые показывают, кому Миша подписал открытки, а синим – кто подписал Мише.

Методические указания: при решении этой задачи имена можно обозначить первой буквой, изобразить граф, изображая поздравления стрелками. После стрелки обвести соответствующим цветом.

Проверять решение можно как постепенно, открывая поэтапно стрелки, так и целиком открыв весь граф на слайде электронного варианта «Сборника…».

 

З адача 21. Из каждой пары чисел 63, 9, 7, 70 составь всевозможные суммы. Выбери граф, который соответствует данному заданию.

 

 

Методические указания: цель данной задачи – формировать умение читать граф. Стрелочка вокруг каждого числа обозначает, что к данному числу прибавляют то же число.

Задача 25. Сколько разностей можно составить из чисел 30, 25, 17, 9, если для их составления брать два числа? Проверь свой ответ, изобразив граф.

Методические указания: данную задачу надо сначала решить методом организованного перебора, подсчитать количество разностей, а затем построить соответствующий граф. Проверить получившееся решение можно с помощью электронного варианта «Сборника…».

 

Далее мы предлагаем познакомить учащихся с применением одной из разновидностей графа – деревом возможных вариантов при решении комбинаторных задач.

 

З адача 26. Нарисуй башенки, которые «зашифрованы», для этого пройди по всем возможным путям от верхней точки до нижних.

верхний кубик

 

 

средний кубик

 

нижний кубик

Методические указания: можно дать возможность учащимся самим, без помощи учителя, нарисовать башенки, а затем лишь проверить, открывая постепенно решение на слайде электронного варианта «Сборника…». См. также методические указания к задаче 27.

Задачу 26 и задачу 27 целесообразно предлагать учащимся на одном уроке.

 

Задача 2. На первой прямой взяты три точки, а на параллельной ей прямой четыре точки. Сколько существует треугольников, вершинами которых являются эти точки?

Решение. Треугольник однозначно определяется тремя точками-вершинами, не принадлежащими одной прямой. Если взять в качестве вершины треугольника одну из трех точек на первой прямой, то, чтобы получить треугольник, на второй прямой надо выбрать две точки из четырех имеющихся. Если одну точку - вершину из четырех выбираем на второй прямой, то две точки из трех надо выбрать на первой прямой. Применяя правила умножения и сложения, найдем 30 треугольников.

«Неформальный» способ решения на первый план выводит сам процесс составления различных ком