Пусть 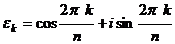 первообразный корень степени
первообразный корень степени  из единицы. Допустим, что
из единицы. Допустим, что  . Тогда
. Тогда 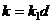 и
и 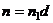 , тогда:
, тогда: 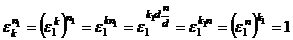 , то есть
, то есть 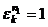 , где
, где 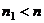 , противоречие.
, противоречие.
Достаточность. Пусть 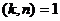 , но пусть при этом
, но пусть при этом  не является первообразным корнем, то есть существует
не является первообразным корнем, то есть существует 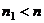 , для которого
, для которого 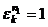 . Тогда
. Тогда 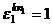 .
.
Докажем, что 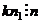 , и тогда
, и тогда 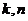 не будут взаимно просты.
не будут взаимно просты.
Пусть 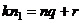 . Тогда
. Тогда 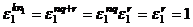 .
.
Получили 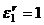 , но остаток
, но остаток 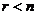 , а корень
, а корень 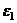 первообразный. Противоречие с тем, что
первообразный. Противоречие с тем, что 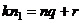 (делится с остатком).
(делится с остатком).
Значит, 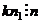 . Но так как
. Но так как 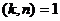 , то
, то 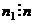 , но оно было меньше, чем
, но оно было меньше, чем  . Противоречие.
. Противоречие.
Теорема 3. Корень степени  из 1 является первообразным
из 1 является первообразным 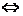 он является образующим циклической группы
он является образующим циклической группы 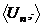 .
.
Доказательство. Необходимость. Пусть 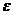 - какой-нибудь первообразный корень степени
- какой-нибудь первообразный корень степени  из 1. Тогда при любом целом
из 1. Тогда при любом целом 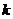 , число
, число 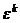 тоже будет корнем степени
тоже будет корнем степени  из 1, так как
из 1, так как 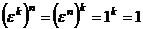 .
.
Рассмотрим 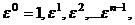 все они являются корнями степени
все они являются корнями степени  из 1. И среди них нет равных, так как если
из 1. И среди них нет равных, так как если 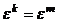 , то
, то 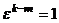 , где
, где 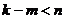 , что невозможно, так как
, что невозможно, так как 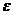 - первообразный корень степени
- первообразный корень степени  . Итак,
. Итак, 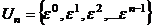 =
= 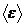 .
.
Достаточность. Пусть 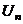 =
= 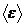 . Докажем, что этот корень
. Докажем, что этот корень 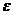 первообразный. Пусть
первообразный. Пусть 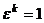 при
при 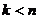 .
.
Тогда 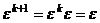 , для всех степеней, больших чем
, для всех степеней, больших чем 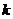 , повторяются уже учтённые корни, то есть
, повторяются уже учтённые корни, то есть 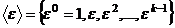 , но тогда это не группа
, но тогда это не группа 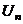 , так как в группе
, так как в группе 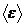 получилось меньше чем
получилось меньше чем  элементов.
элементов.
Противоречие.
Пример. -1 не первообразный корень степени 4 из 1; возводя в разные степени, никогда не получим i или –i.
ЛЕКЦИЯ 15. 1.4.2021
Лемма. Сумма всех корней степени  из 1 равна 0.
из 1 равна 0.
Доказательство. Пусть 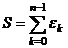 .
.
Но 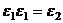 ,
, 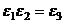 ,...,
,..., 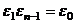 (при умножении на
(при умножении на 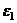 каждая точка поворачивается на угол
каждая точка поворачивается на угол 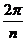 и переходит в следующую).
и переходит в следующую).
Тогда 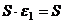 , так как это сумма тех же
, так как это сумма тех же  комплексных чисел. Но при этом
комплексных чисел. Но при этом 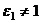 . Значит,
. Значит, 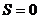 .
.
Области в комплексной плоскости и неравенства, задающие их.
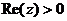 правая полуплоскость.
правая полуплоскость.
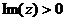 верхняя полуплоскость.
верхняя полуплоскость.
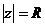 - окружность радиуса R вокруг начала координат.
- окружность радиуса R вокруг начала координат.
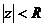 - круг радиуса R вокруг начала координат.
- круг радиуса R вокруг начала координат.
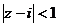 это круг радиуса 1 вокруг точки
это круг радиуса 1 вокруг точки 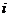 . Это неравенство задаёт следующее условие: удаление числа
. Это неравенство задаёт следующее условие: удаление числа 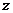 от фиксированного числа
от фиксированного числа 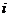 не превышает 1. Можно непосредственно преобразовать в уравнение круга в плоскости:
не превышает 1. Можно непосредственно преобразовать в уравнение круга в плоскости: 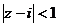
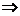

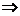
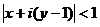
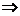
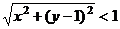
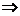
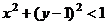 а это уравнение круга, центр которого в точке (0,1), то есть как раз в точке
а это уравнение круга, центр которого в точке (0,1), то есть как раз в точке 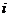 . Чертёж:
. Чертёж:
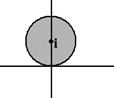
Пример. 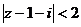
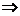
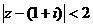 это круг радиуса 2 с центром в точке
это круг радиуса 2 с центром в точке 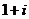 , то есть точке (1,1) в плоскости.
, то есть точке (1,1) в плоскости.
Пример. Множество 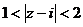 это кольцо вокруг точки
это кольцо вокруг точки 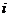 .
.
Пример. 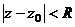 это круг радиуса
это круг радиуса 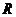 вокруг точки
вокруг точки 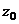 .
.
Функции комплексного переменного.
Обобщим на комплексную плоскость синус и косинус.
Верны такие формулы: 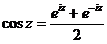 ,
, 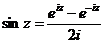 .
.
Доказательство.
Рассмотрим для действительного числа 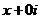 и покажем, что данные функции, а именно
и покажем, что данные функции, а именно 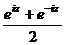 и
и 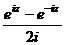 , приведут именно к обычному синусу и косинусу действительного числа, т.е. они обобщают синус и косинус. Используя формулу Эйлера,
, приведут именно к обычному синусу и косинусу действительного числа, т.е. они обобщают синус и косинус. Используя формулу Эйлера,
1) 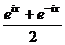 =
= 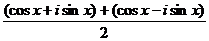 =
= 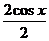 =
= 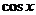
2) 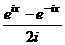 =
=  =
= 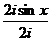 =
= 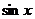
Неограниченность синуса и косинуса в комплексной плоскости.
Пример. 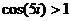 .
.
Вычислим: 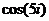 =
= 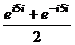 =
= 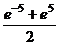
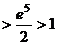 .
.
Логарифм комплексного числа.
Обобщённый логарифм вводится с помощью формулы:
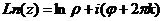 (
(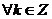 )
)
Доказательство.
Проверим, совпадает ли 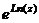 и
и 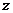 при любом целом
при любом целом 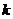 .
.
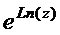 =
=  =
= 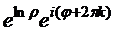 =
= 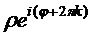 =
=
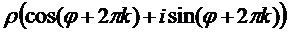 =
=
синус и косинус не зависят от прибавления угла, кратного 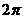 , поэтому получаем
, поэтому получаем 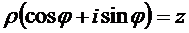 .
.
А это уже и есть тригонометрическая форма комплексного числа.
Итак, 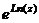 =
= 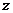 .
.
Если вычислять логарифм положительного действительного числа, то 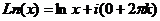 , т.е. одна точка из бесконечного множества попадает на действительную ось, потому что исходный угол
, т.е. одна точка из бесконечного множества попадает на действительную ось, потому что исходный угол 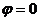 . Для любого числа, которое не является действительным положительным,
. Для любого числа, которое не является действительным положительным, 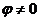 , поэтому происходит сдвиг этой последовательности на часть деления, и ни одна точка не попадёт на действительную ось.
, поэтому происходит сдвиг этой последовательности на часть деления, и ни одна точка не попадёт на действительную ось.
Пример. Вычислить 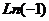 .
.
Здесь 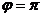 ,
, 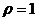 . Поэтому
. Поэтому 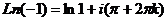 =
= 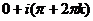 .
.
Точки в комплексной плоскости: 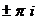 ,
, 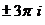 ,
, 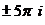 , и так далее.
, и так далее.
Ни одного значения на действительной оси нет, и здесь, по сравнению со значениями логарифма положительного числа, сдвиг на половину деления: одна точка ушла вверх с действительной оси, а другая ещё не достигла этой оси. Чертёж:
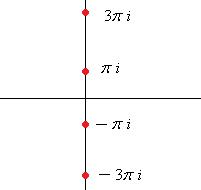
Здесь легко сделать и проверку: 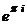 =
= 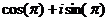 =
= 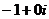 =
= 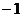 , то есть действительно,
, то есть действительно, 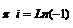 .
.
Пример. Вычислить 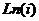 .
.
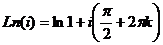 =
= 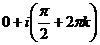 . Последовательность значений такова:
. Последовательность значений такова: 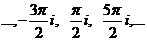 каждая соседняя пара отличается на
каждая соседняя пара отличается на 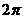 по высоте. Здесь сдвиг вверх всего на четверть деления, а не на половину, как для
по высоте. Здесь сдвиг вверх всего на четверть деления, а не на половину, как для 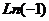 .
.
1) При фиксированном модуле исходного числа и увеличении его аргумента, эта последовательность точек плывёт вверх, при полном повороте на 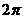 как раз следующая точка попадёт на место предыдущей.
как раз следующая точка попадёт на место предыдущей.
2) При фиксированном аргументе исходного числа и увеличении его модуля, эта последовательность точек плывёт вправо, если исходная точка внутри единичной окружности то множество значений логарифма в левой полуплоскости, так как 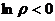 , а если вне единичной окружности, то в правой полуплоскости.
, а если вне единичной окружности, то в правой полуплоскости.
Динамическая анимация, показывающая поведение значений 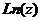 в зависимости от колебаний модуля или аргумента
в зависимости от колебаний модуля или аргумента 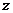 , показана в следующем обучающем видеоролике:
, показана в следующем обучающем видеоролике:
http://www.youtube.com/watch?v=LKFFn-TSLd0
Замечание. Единственная точка в комплексной плоскости, для которой не существует логарифма, это 0. Ведь в этом случае 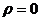 , и не существует
, и не существует 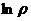 .
.
Пример. Вычислить 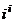 .
.
Решение. Представим 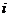 , расположенную в основании, в виде
, расположенную в основании, в виде 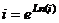 . Тогда
. Тогда 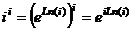 , причём чуть выше мы вычисляли
, причём чуть выше мы вычисляли
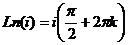 . Тогда
. Тогда 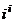 =
= 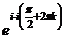 =
= 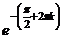 т.е. получается бесконечное множество точек на действительной оси.
т.е. получается бесконечное множество точек на действительной оси.
Для всякой функции 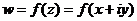 можно отдельно выделить действительную и мнимую части, и представить в виде
можно отдельно выделить действительную и мнимую части, и представить в виде
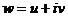 . Таким образом, возникают понятия: действительная и мнимая часть функции, обозначения:
. Таким образом, возникают понятия: действительная и мнимая часть функции, обозначения: 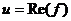 ,
, 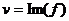 . Итак, комплексной функции можно поставить в соответствие некоторое отображение из
. Итак, комплексной функции можно поставить в соответствие некоторое отображение из 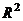 в
в 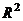 , а именно
, а именно 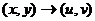 . Но график такого отображения был бы в 4-мерном пространстве, поэтому изобразить его в нашем 3-мерном пространстве невозможно. Но мы можем пользоваться неким подобием графика, а именно, рассматривать чертёж искажений плоскости, изучать, в какие линии отображаются горизонтальные либо вертикальные линии из исходной плоскости.
. Но график такого отображения был бы в 4-мерном пространстве, поэтому изобразить его в нашем 3-мерном пространстве невозможно. Но мы можем пользоваться неким подобием графика, а именно, рассматривать чертёж искажений плоскости, изучать, в какие линии отображаются горизонтальные либо вертикальные линии из исходной плоскости.
Пример. Разложить 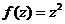 на сумму действительной и мнимой частей, изобразить искажения плоскости при переходе
на сумму действительной и мнимой частей, изобразить искажения плоскости при переходе 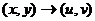 .
.
1) 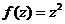 =
= 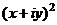 =
= 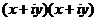 =
= 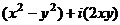 .
.
Таким образом, 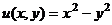 ,
, 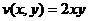 .
.
Чтобы исследовать, куда переходят горизонтальные прямые, зафиксируем 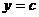 , при этом
, при этом 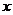 изменяется от
изменяется от 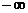 до
до 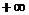 , пусть движение задано с помощью параметра
, пусть движение задано с помощью параметра 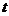 :
:
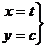
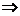
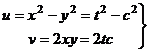 .
.
Чтобы составить уравнение, взаимосвязывающее 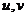 , и узнать, какая это кривая, исключим параметр
, и узнать, какая это кривая, исключим параметр 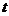 , выразив из второго уравнения:
, выразив из второго уравнения: 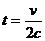 , тогда
, тогда 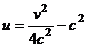 . Это парабола, лежащая на боку, ветвями направленная вправо, причём чем больше
. Это парабола, лежащая на боку, ветвями направленная вправо, причём чем больше 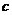 , тем левее вершина, и тем более пологая парабола получается, ведь
, тем левее вершина, и тем более пологая парабола получается, ведь 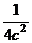 при этом меньше. А если
при этом меньше. А если 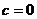 , то возникает предельный случай: обе ветви смыкаются в одну линию и образуют правую полуось. Действительная ось отображается на правую полуось в плоскости
, то возникает предельный случай: обе ветви смыкаются в одну линию и образуют правую полуось. Действительная ось отображается на правую полуось в плоскости 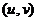 .
.
Аналогично, для какой-либо вертикальной прямой:
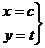
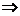
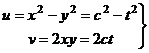 . Тогда, исключая параметр
. Тогда, исключая параметр 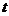 , получим
, получим 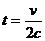
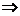
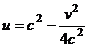 . Это параболы, направленные ветвями влево, симметричные тем, что были рассмотрены чуть выше.
. Это параболы, направленные ветвями влево, симметричные тем, что были рассмотрены чуть выше.
На чертеже зелёным цветом показаны горизонтальные прямые и их образы при отображении 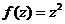 , а красным - вертикальные прямые и их образы:
, а красным - вертикальные прямые и их образы:
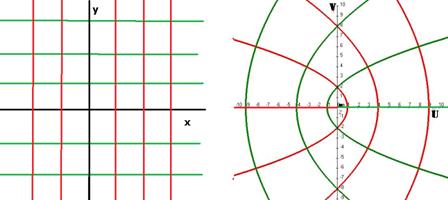
Примечание. 4-мерный график можно было бы рассматривать таким образом: нужно как минимум 4 проекции на координатные пространства, а именно 0xyz, 0xzw, 0xyw, 0yzw.
Либо можно рассмотреть 2 поверхности, построенные по функциям 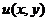 и
и 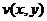 .
.
Линейные пространства над С
Над полем комплексных чисел тоже, как и над R, можно рассматривать линейные пространства различной размерности. Рассмотрим, чем отличается строение скалярного произведения в этом случае, и каким будет аналог евклидового пространства.
Напомним, что в линейном пространстве 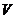 над полем
над полем 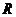 задано евклидово скалярное произведение, если задана функция
задано евклидово скалярное произведение, если задана функция  , т.е. каждой паре векторов можно однозначно поставить в соответствие число
, т.е. каждой паре векторов можно однозначно поставить в соответствие число 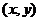 , причём:
, причём:
1) 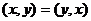
2) 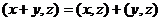 ,
, 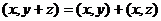
3)  ,
, 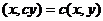
4) 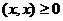 , причём
, причём 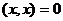
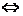
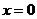 .
.
Нормой (модулем) вектора 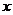 называется число
называется число 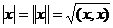 .
.
Эрмитово скалярное произведение 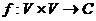 :
:
1) 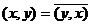 , и в частности,
, и в частности, 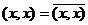
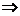
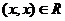 , поэтому норма также определяется как действительная величина.
, поэтому норма также определяется как действительная величина.
2) 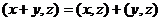 ,
, 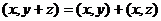
Отличие в том, как выносится константа со 2 места:
3) 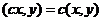 ,
, 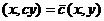 ,
,
4) 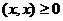 , причём
, причём 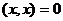
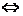
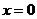 .
.
(полуторалинейная форма). Унитарное пространство.
Гауссовы числа.
Можно рассматривать множество комплексных чисел только с целыми координатами, G = 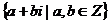 , они образуют кольцо, что нетрудно доказать, так как коммутативность, ассоциативность и дистрибутивность следует из комм., асс., дистрибутивности в поле С, отличие в том, что не каждый элемент обратим. Обратимы, к примеру, некоторые числа:
, они образуют кольцо, что нетрудно доказать, так как коммутативность, ассоциативность и дистрибутивность следует из комм., асс., дистрибутивности в поле С, отличие в том, что не каждый элемент обратим. Обратимы, к примеру, некоторые числа:  ,
, 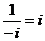 ,
, 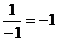 ,
, 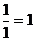 .
.
Если модуль числа больше 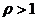 , то модуль обратного меньше 1, и тогда оно не является гауссовым числом. Поэтому множество всех мультипликативно обратимых элементов ограничивается числами
, то модуль обратного меньше 1, и тогда оно не является гауссовым числом. Поэтому множество всех мультипликативно обратимых элементов ограничивается числами 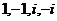 , они называются делителями единицы и образуют группу.
, они называются делителями единицы и образуют группу.
Два комплексных числа называются ассоциированными, если они отличаются на множитель, являющийся делителем единицы.
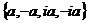 - множество попарно ассоциированных элементов.
- множество попарно ассоциированных элементов.
Нормой гауссова числа называется квадрат его модуля:
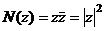 .
.
Деление с остатком.
Для любых 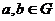 существуют
существуют 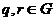 , такие, что
, такие, что 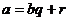 , и
, и 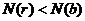 .
.
Пример. Поделить  на
на 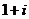 с остатком в кольце гауссовых чисел.
с остатком в кольце гауссовых чисел.
Сначала разделим обычным образом, получив дробные значения действительной и мнимой части. 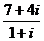 =
= 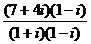 =
= 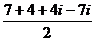 =
= 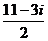 =
= 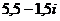 . Берём целую часть по каждой координате,
. Берём целую часть по каждой координате,  .
.
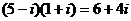 , исходное число было
, исходное число было  . Таким образом,
. Таким образом,
 =
= 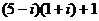 , остаток равен 1.
, остаток равен 1.
Впрочем, гауссовы числа - линейно не упорядоченное множество, поэтому деление не однозначно: можем округлить до целого:
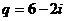 , тогда
, тогда 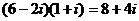 .
.
Верно также и  =
= 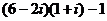 , остаток
, остаток 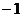 .
.
* Если при делении получается 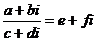 , где
, где 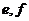 целые, то говорят, что
целые, то говорят, что 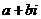 делится на
делится на 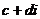 без остатка.
без остатка.
* В связи с этим, вводится понятие НОД аналогично тому, как было в кольце Z. Однако, из-за ассоциированности, НОД определяется не единственным образом.
Обратим внимание на то, что некоторые простые действительные числа не являются простыми гауссовыми: например,
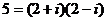 =
= 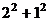 ,
, 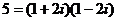
- существует даже 2 разных разложения. Аналогично:
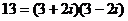 ,
, 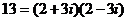 .
. 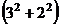
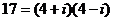 ,
, 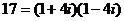 .
. 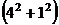
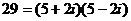 ,
, 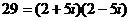 .
. 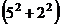 .
.
Обратим внимание на то, что во всех этих примерах числа вида 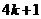 , то есть имеющие остаток 1 при делении на 4. Сейчас мы докажем, что это не случайно, и только такие простые числа имеют разложение в виде произведения двух сопряжённых гауссовых.
, то есть имеющие остаток 1 при делении на 4. Сейчас мы докажем, что это не случайно, и только такие простые числа имеют разложение в виде произведения двух сопряжённых гауссовых.
Лемма 1. Если 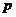 простое и является произведением двух гауссовых чисел, то оно должно иметь вид
простое и является произведением двух гауссовых чисел, то оно должно иметь вид 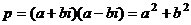 .
.
Доказательство.
1) Доказывали ранее (см. практику), что если действительное число есть произведение двух комплексных, то одно комплексное обязательно сопряжённое к другому, с точностью до действительного множителя, то есть  .
.
2) Если  , то
, то 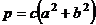 , тогда оно не было бы простым, так как распадалось бы действительные на множители.
, тогда оно не было бы простым, так как распадалось бы действительные на множители.
Таким образом, единственный вариант, это 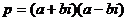 при
при 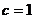 .
.
Лемма 2. Числа вида 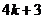 не могут быть разложены в произведение двух сопряжённых.
не могут быть разложены в произведение двух сопряжённых.
Доказательство. Допустим, что 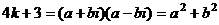 .
.
Докажем, что числа вида 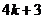 не могут быть представлены в виде суммы квадратов.
не могут быть представлены в виде суммы квадратов.
Если число 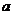 или
или 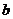 чётное, то его квадрат имеет вид
чётное, то его квадрат имеет вид 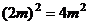 , то есть имеет остаток 0 при делении на 4
, то есть имеет остаток 0 при делении на 4
Если число 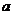 или
или 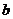 нечётное, то его квадрат имеет вид
нечётное, то его квадрат имеет вид  , то есть имеет остаток 1 при делении на 4.
, то есть имеет остаток 1 при делении на 4.
Таким образом, сумма квадратов двух чётных имеет остаток 0, для чётного и нечётного остаток 1, для двух нечётных остаток 2, но ни в каком случае он не может быть равен 3.
Следствие. Из леммы 2 следует, что если 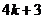 простое нечётное число, то оно является и простым гауссовым.
простое нечётное число, то оно является и простым гауссовым.
Таким образом, составные гауссовы числа могут быть только среди чисел вида 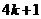 . Кроме того, мы докажем менее очевидный факт: что все простые числа вида
. Кроме того, мы докажем менее очевидный факт: что все простые числа вида 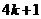 представимы в виде произведения сопряжённых гауссовых чисел.
представимы в виде произведения сопряжённых гауссовых чисел.
Лемма 3. Если простое нечётное число имеет вид 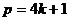 , то существует
, то существует 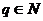 , такое, что
, такое, что  .
.
Доказательство. По теореме Вильсона, для простого числа:
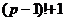 делится на
делится на 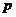 . В этом случае
. В этом случае 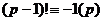 , кроме того, очевидно,
, кроме того, очевидно, 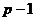 чётное. Сопоставим остатки крайних чисел в этом факториале, затем соседних с ними и т.д.
чётное. Сопоставим остатки крайних чисел в этом факториале, затем соседних с ними и т.д.
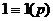 ,
, 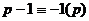 ,
, 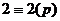 ,
,  ,... таким образом, до
,... таким образом, до 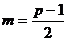 выполняется закономерность:
выполняется закономерность: 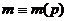 ,
, 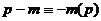 .
.
Тогда 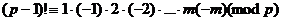 , то есть
, то есть
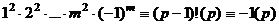 .
.
Если 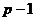 не делится на 4, то
не делится на 4, то 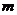 нечётно, и
нечётно, и
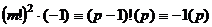 , тогда
, тогда 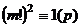 .
.
Если 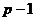 делится на 4, то
делится на 4, то 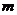 чётно, и
чётно, и 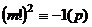 .
.
Таким образом, существует 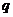 , равное
, равное 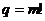 , такое что
, такое что 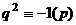 .
.
Теорема Эйлера-Ферма. Если простое нечётное число имеет вид 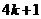 , то оно представимо в виде суммы квадратов
, то оно представимо в виде суммы квадратов 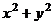 .
.
Доказательство.
Рассмотрим множество пар 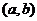 , где
, где 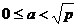 ,
, 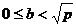 .
.
Строго меньше, так как 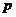 простое, значит оно не может делиться на целое число, то есть
простое, значит оно не может делиться на целое число, то есть 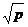 точно не будет целым.
точно не будет целым.
Если 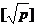 обозначает целую часть корня из
обозначает целую часть корня из 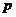 , то количество таких пар чисел составляет
, то количество таких пар чисел составляет 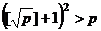 .
.
Напр, если p=17 (25 пар) 0 1 2 3 4
Рассмотрим для произвольного 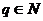 все числа вида
все числа вида 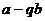 .
.
Мощность множества пар больше, чем 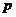 . При этом множество возможных остатков
. При этом множество возможных остатков 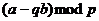 имеет максимальную мощность меньше или равную
имеет максимальную мощность меньше или равную 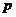 . Значит, для каких-то двух пар
. Значит, для каких-то двух пар 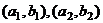 остатки одинаковы:
остатки одинаковы:
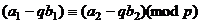
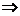
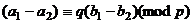 .
.
Обозначив 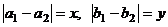 , получим
, получим
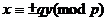 , тогда
, тогда 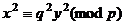 .
.
Вспомним, что согласно предыдущей лемме, для числа вида 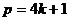 , то существует
, то существует 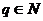 , такое, что
, такое, что  .
.
Тогда выберем такое 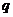 и получим
и получим 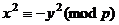 , то есть
, то есть 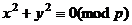 , что означает
, что означает 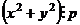 .
.
Так как 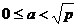 ,
, 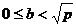 , то для квадратов модулей разностей
, то для квадратов модулей разностей 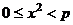 ,
, 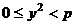 , и
, и 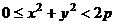 . При этом 0 быть не может, так как две пары были разные, тогда
. При этом 0 быть не может, так как две пары были разные, тогда 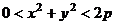 .
.
Единственное число во множестве 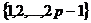 , делящееся на
, делящееся на 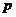 , это само
, это само 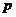 , так как 0 и
, так как 0 и  не принадлежат множеству.
не принадлежат множеству.
Тогда 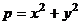 , что и требовалось доказать.
, что и требовалось доказать.
Следствие. Если простое нечётное число имеет вид 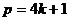 , то оно является составным гауссовым числом:
, то оно является составным гауссовым числом: 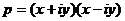 ,
, 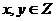 .
.
ЛЕКЦИЯ 16. 3.4.2021
Замкнутость сумм квадратов относительно умножения (2 способа, обычный и через модули комплексных).
Лемма. Произведение двух сумм квадратов целых чисел также представляется в виде суммы квадратов:
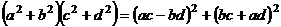 .
.



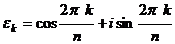 первообразный корень степени
первообразный корень степени  из единицы. Допустим, что
из единицы. Допустим, что  . Тогда
. Тогда 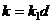 и
и 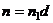 , тогда:
, тогда: 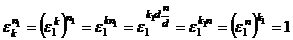 , то есть
, то есть 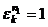 , где
, где 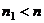 , противоречие.
, противоречие.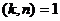 , но пусть при этом
, но пусть при этом  не является первообразным корнем, то есть существует
не является первообразным корнем, то есть существует 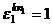 .
.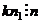 , и тогда
, и тогда 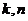 не будут взаимно просты.
не будут взаимно просты.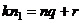 . Тогда
. Тогда 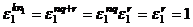 .
.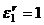 , но остаток
, но остаток 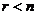 , а корень
, а корень 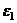 первообразный. Противоречие с тем, что
первообразный. Противоречие с тем, что 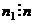 , но оно было меньше, чем
, но оно было меньше, чем 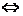 он является образующим циклической группы
он является образующим циклической группы 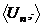 .
.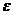 - какой-нибудь первообразный корень степени
- какой-нибудь первообразный корень степени 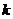 , число
, число 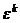 тоже будет корнем степени
тоже будет корнем степени 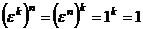 .
. 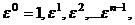 все они являются корнями степени
все они являются корнями степени 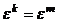 , то
, то 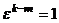 , где
, где 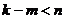 , что невозможно, так как
, что невозможно, так как 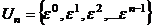 =
= 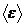 .
. 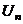 =
= 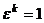 при
при 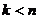 .
. 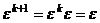 , для всех степеней, больших чем
, для всех степеней, больших чем 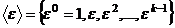 , но тогда это не группа
, но тогда это не группа 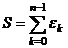 .
. 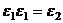 ,
, 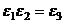 ,...,
,..., 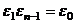 (при умножении на
(при умножении на 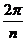 и переходит в следующую).
и переходит в следующую). 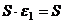 , так как это сумма тех же
, так как это сумма тех же 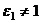 . Значит,
. Значит, 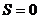 .
.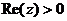 правая полуплоскость.
правая полуплоскость.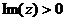 верхняя полуплоскость.
верхняя полуплоскость.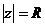 - окружность радиуса R вокруг начала координат.
- окружность радиуса R вокруг начала координат. 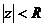 - круг радиуса R вокруг начала координат.
- круг радиуса R вокруг начала координат. 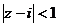 это круг радиуса 1 вокруг точки
это круг радиуса 1 вокруг точки 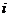 . Это неравенство задаёт следующее условие: удаление числа
. Это неравенство задаёт следующее условие: удаление числа 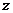 от фиксированного числа
от фиксированного числа 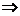

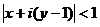
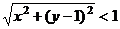
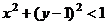 а это уравнение круга, центр которого в точке (0,1), то есть как раз в точке
а это уравнение круга, центр которого в точке (0,1), то есть как раз в точке 
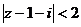
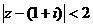 это круг радиуса 2 с центром в точке
это круг радиуса 2 с центром в точке 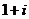 , то есть точке (1,1) в плоскости.
, то есть точке (1,1) в плоскости.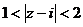 это кольцо вокруг точки
это кольцо вокруг точки 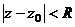 это круг радиуса
это круг радиуса 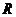 вокруг точки
вокруг точки 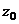 .
.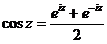 ,
, 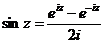 .
.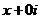 и покажем, что данные функции, а именно
и покажем, что данные функции, а именно 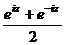 и
и 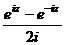 , приведут именно к обычному синусу и косинусу действительного числа, т.е. они обобщают синус и косинус. Используя формулу Эйлера,
, приведут именно к обычному синусу и косинусу действительного числа, т.е. они обобщают синус и косинус. Используя формулу Эйлера,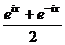 =
= 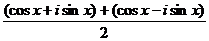 =
= 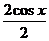 =
= 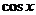
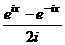 =
=  =
= 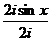 =
= 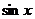
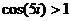 .
.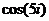 =
= 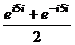 =
= 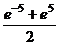
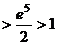 .
.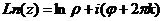 (
(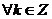 )
)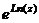 и
и 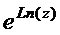 =
=  =
= 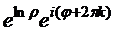 =
= 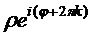 =
=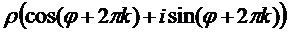 =
=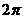 , поэтому получаем
, поэтому получаем 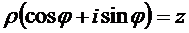 .
.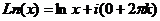 , т.е. одна точка из бесконечного множества попадает на действительную ось, потому что исходный угол
, т.е. одна точка из бесконечного множества попадает на действительную ось, потому что исходный угол 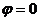 . Для любого числа, которое не является действительным положительным,
. Для любого числа, которое не является действительным положительным, 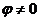 , поэтому происходит сдвиг этой последовательности на часть деления, и ни одна точка не попадёт на действительную ось.
, поэтому происходит сдвиг этой последовательности на часть деления, и ни одна точка не попадёт на действительную ось.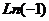 .
.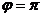 ,
, 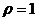 . Поэтому
. Поэтому 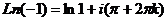 =
= 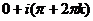 .
.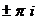 ,
, 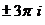 ,
, 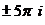 , и так далее.
, и так далее.
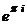 =
= 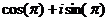 =
= 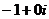 =
= 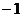 , то есть действительно,
, то есть действительно, 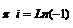 .
.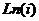 .
.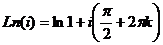 =
= 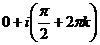 . Последовательность значений такова:
. Последовательность значений такова: 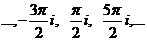 каждая соседняя пара отличается на
каждая соседняя пара отличается на 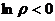 , а если вне единичной окружности, то в правой полуплоскости.
, а если вне единичной окружности, то в правой полуплоскости.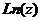 в зависимости от колебаний модуля или аргумента
в зависимости от колебаний модуля или аргумента 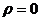 , и не существует
, и не существует 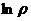 .
.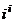 .
.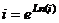 . Тогда
. Тогда 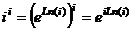 , причём чуть выше мы вычисляли
, причём чуть выше мы вычисляли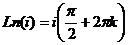 . Тогда
. Тогда 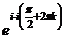 =
= 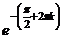 т.е. получается бесконечное множество точек на действительной оси.
т.е. получается бесконечное множество точек на действительной оси.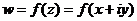 можно отдельно выделить действительную и мнимую части, и представить в виде
можно отдельно выделить действительную и мнимую части, и представить в виде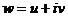 . Таким образом, возникают понятия: действительная и мнимая часть функции, обозначения:
. Таким образом, возникают понятия: действительная и мнимая часть функции, обозначения: 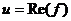 ,
, 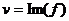 . Итак, комплексной функции можно поставить в соответствие некоторое отображение из
. Итак, комплексной функции можно поставить в соответствие некоторое отображение из 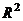 в
в 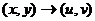 . Но график такого отображения был бы в 4-мерном пространстве, поэтому изобразить его в нашем 3-мерном пространстве невозможно. Но мы можем пользоваться неким подобием графика, а именно, рассматривать чертёж искажений плоскости, изучать, в какие линии отображаются горизонтальные либо вертикальные линии из исходной плоскости.
. Но график такого отображения был бы в 4-мерном пространстве, поэтому изобразить его в нашем 3-мерном пространстве невозможно. Но мы можем пользоваться неким подобием графика, а именно, рассматривать чертёж искажений плоскости, изучать, в какие линии отображаются горизонтальные либо вертикальные линии из исходной плоскости.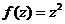 на сумму действительной и мнимой частей, изобразить искажения плоскости при переходе
на сумму действительной и мнимой частей, изобразить искажения плоскости при переходе 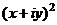 =
= 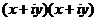 =
= 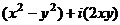 .
.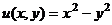 ,
, 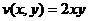 .
.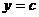 , при этом
, при этом 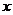 изменяется от
изменяется от 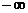 до
до 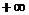 , пусть движение задано с помощью параметра
, пусть движение задано с помощью параметра 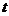 :
: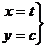
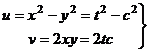 .
.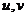 , и узнать, какая это кривая, исключим параметр
, и узнать, какая это кривая, исключим параметр 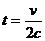 , тогда
, тогда 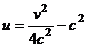 . Это парабола, лежащая на боку, ветвями направленная вправо, причём чем больше
. Это парабола, лежащая на боку, ветвями направленная вправо, причём чем больше 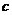 , тем левее вершина, и тем более пологая парабола получается, ведь
, тем левее вершина, и тем более пологая парабола получается, ведь 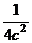 при этом меньше. А если
при этом меньше. А если 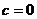 , то возникает предельный случай: обе ветви смыкаются в одну линию и образуют правую полуось. Действительная ось отображается на правую полуось в плоскости
, то возникает предельный случай: обе ветви смыкаются в одну линию и образуют правую полуось. Действительная ось отображается на правую полуось в плоскости 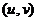 .
.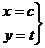
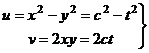 . Тогда, исключая параметр
. Тогда, исключая параметр 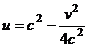 . Это параболы, направленные ветвями влево, симметричные тем, что были рассмотрены чуть выше.
. Это параболы, направленные ветвями влево, симметричные тем, что были рассмотрены чуть выше.
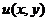 и
и 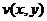 .
.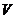 над полем
над полем  , т.е. каждой паре векторов можно однозначно поставить в соответствие число
, т.е. каждой паре векторов можно однозначно поставить в соответствие число 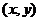 , причём:
, причём: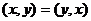
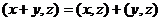 ,
, 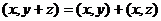
 ,
, 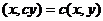
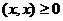 , причём
, причём 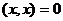
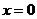 .
.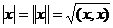 .
.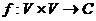 :
: 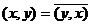 , и в частности,
, и в частности, 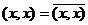
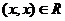 , поэтому норма также определяется как действительная величина.
, поэтому норма также определяется как действительная величина. 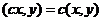 ,
, 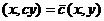 ,
, 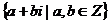 , они образуют кольцо, что нетрудно доказать, так как коммутативность, ассоциативность и дистрибутивность следует из комм., асс., дистрибутивности в поле С, отличие в том, что не каждый элемент обратим. Обратимы, к примеру, некоторые числа:
, они образуют кольцо, что нетрудно доказать, так как коммутативность, ассоциативность и дистрибутивность следует из комм., асс., дистрибутивности в поле С, отличие в том, что не каждый элемент обратим. Обратимы, к примеру, некоторые числа:  ,
, 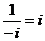 ,
, 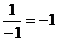 ,
, 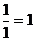 .
. 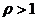 , то модуль обратного меньше 1, и тогда оно не является гауссовым числом. Поэтому множество всех мультипликативно обратимых элементов ограничивается числами
, то модуль обратного меньше 1, и тогда оно не является гауссовым числом. Поэтому множество всех мультипликативно обратимых элементов ограничивается числами 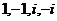 , они называются делителями единицы и образуют группу.
, они называются делителями единицы и образуют группу. 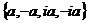 - множество попарно ассоциированных элементов.
- множество попарно ассоциированных элементов. 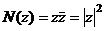 .
. 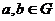 существуют
существуют 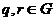 , такие, что
, такие, что 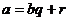 , и
, и 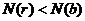 .
. на
на 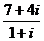 =
= 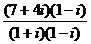 =
= 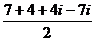 =
= 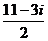 =
= 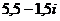 . Берём целую часть по каждой координате,
. Берём целую часть по каждой координате,  .
. 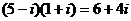 , исходное число было
, исходное число было 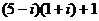 , остаток равен 1.
, остаток равен 1.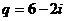 , тогда
, тогда 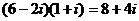 .
. 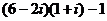 , остаток
, остаток 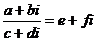 , где
, где 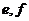 целые, то говорят, что
целые, то говорят, что 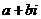 делится на
делится на 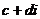 без остатка.
без остатка.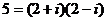 =
= 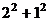 ,
, 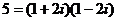
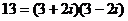 ,
, 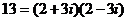 .
. 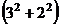
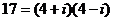 ,
, 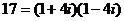 .
. 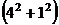
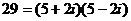 ,
, 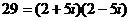 .
. 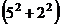 .
. 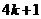 , то есть имеющие остаток 1 при делении на 4. Сейчас мы докажем, что это не случайно, и только такие простые числа имеют разложение в виде произведения двух сопряжённых гауссовых.
, то есть имеющие остаток 1 при делении на 4. Сейчас мы докажем, что это не случайно, и только такие простые числа имеют разложение в виде произведения двух сопряжённых гауссовых.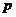 простое и является произведением двух гауссовых чисел, то оно должно иметь вид
простое и является произведением двух гауссовых чисел, то оно должно иметь вид 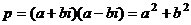 .
.  .
. 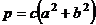 , тогда оно не было бы простым, так как распадалось бы действительные на множители.
, тогда оно не было бы простым, так как распадалось бы действительные на множители.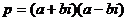 при
при 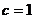 .
. 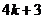 не могут быть разложены в произведение двух сопряжённых.
не могут быть разложены в произведение двух сопряжённых. 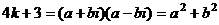 .
.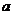 или
или 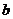 чётное, то его квадрат имеет вид
чётное, то его квадрат имеет вид 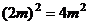 , то есть имеет остаток 0 при делении на 4
, то есть имеет остаток 0 при делении на 4 , то есть имеет остаток 1 при делении на 4.
, то есть имеет остаток 1 при делении на 4.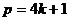 , то существует
, то существует 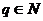 , такое, что
, такое, что  .
.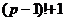 делится на
делится на 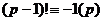 , кроме того, очевидно,
, кроме того, очевидно, 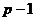 чётное. Сопоставим остатки крайних чисел в этом факториале, затем соседних с ними и т.д.
чётное. Сопоставим остатки крайних чисел в этом факториале, затем соседних с ними и т.д.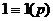 ,
, 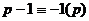 ,
, 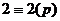 ,
,  ,... таким образом, до
,... таким образом, до 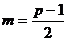 выполняется закономерность:
выполняется закономерность: 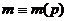 ,
, 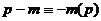 .
.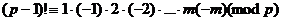 , то есть
, то есть 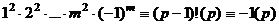 .
. 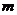 нечётно, и
нечётно, и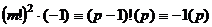 , тогда
, тогда 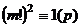 .
. 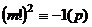 .
. 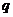 , равное
, равное 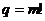 , такое что
, такое что 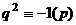 .
. 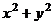 .
. 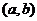 , где
, где 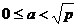 ,
, 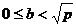 .
.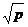 точно не будет целым.
точно не будет целым.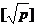 обозначает целую часть корня из
обозначает целую часть корня из 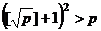 .
.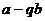 .
. 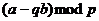 имеет максимальную мощность меньше или равную
имеет максимальную мощность меньше или равную 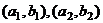 остатки одинаковы:
остатки одинаковы: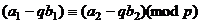
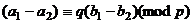 .
. 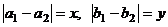 , получим
, получим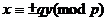 , тогда
, тогда 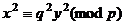 .
. 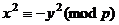 , то есть
, то есть 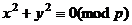 , что означает
, что означает 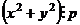 .
. 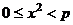 ,
, 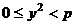 , и
, и 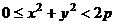 . При этом 0 быть не может, так как две пары были разные, тогда
. При этом 0 быть не может, так как две пары были разные, тогда 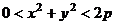 .
.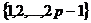 , делящееся на
, делящееся на  не принадлежат множеству.
не принадлежат множеству.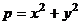 , что и требовалось доказать.
, что и требовалось доказать. 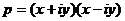 ,
, 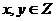 .
. 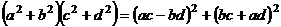 .
. 


