Квадратурная формула Чебышева

Рассмотрим квадратурную формулу

, (8.10)

где 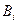- постоянные коэффициенты. Чебышев предположил выбрать абсциссы таким образом, чтобы:

1. коэффициенты были равны между собой;

2. квадратурная формула (8.10) являлась точной для всех полиномов до степени n включительно.

Покажем, как могут быть найдены в этом случае величины и . Полагаем . Учитывая, что при , будем иметь , получаем . Следовательно, квадратурная формула Чебышева имеет вид:

. (8.11)

Для определения абсцисс заметим, что формула (8.11) согласно условию 2 должна быть точной для функции вида . Подставляя эти функции в формулу (8.11), получим систему уравнений:

, (8.12)

из которой могут быть определены неизвестные . Заметим, что система (8.12) при n =8 и n ³10 не имеет действительных решений.

 

Выведем формулу Чебышева с тремя ординатами (n =3).

Для определения абсцисс 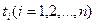имеем систему уравнений:

 

(8.13)

 

Рассмотрим симметрические функции корней:

 

Из системы (8.13) имеем:

 

Отсюда заключаем по теореме Виета, что есть корни вспомогательного уравнения или . Следовательно, можно принять: .

Таким образом, соответствующая формула Чебышева имеет вид .

Чтобы применить квадратурную формулу Чебышева к интегралу вида , следует преобразовать его с помощью подстановки:

, переводящей отрезок в отрезок . Применяя к преобразованному интегралу формулу Чебышева, будем иметь

,

где и - корни системы (8.13).

В таблице приведены значения корней t_i системы (8.12) для n= 1,2…,7.

Таблица 8.1

Значения абсцисс t_i в формуле Чебышева

n	i	ti
	2;1	±0.577350
	3;1	±0.707107
	4;1 3;2	±0.794654 ±0.187592
	5;1 4;2	±0.832498 ±0.374541
	6;1 5;2 4;3	±0.866247 ±0.422519 ±0.266635
	7;1 6;2 5;3	±0.883862 ±0.529657 ±0.323912

Пример 8.3. Вычислить интеграл из предыдущего примера по формуле Чебышева для четырех и для пяти точек в Mathcad.

 

 

 

Оценить точность вычислений.

 

 

 

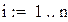
Вычисление интеграла методом Чебышева для 5точек

 

 

 

 

 

 

Рис. 8.3. Решение примера 8.2 в Mathcad

 

Квадратурная формула Гаусса

Полиномы вида называются полиномами Лежандра.

Свойства этих полиномов:

1. , ;

2. , где - любой полином степени k, меньшей n;

3. полином Лежандра имеет n различных и действительных корней, которые расположены на интервале .

Первые пять полиномов Лежандра:

Рассмотрим функцию , заданную на стандартном промежутке . Нужно подобрать точки 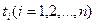и коэффициенты , чтобы квадратурная формула

 

(8.14)

 

была точной для всех полиномов возможной наивысшей степени N. Так как в нашем распоряжении имеются 2n постоянных и , а полином степени 2n-1 определяется 2n коэффициентами, то эта наивысшая степень полинома в общем случае равна N=2n-1.

Для обеспечения равенства (8.14) необходимо и достаточно, чтобы оно было верным при 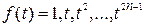. Действительно, полагая и , будем иметь .

Таким образом, учитывая соотношения , заключаем, что для решения поставленной задачи достаточно определить постоянные и из системы 2n уравнений:

(8.15)

Система (8.15) нелинейная, и ее решение обычным путем представляет большие трудности.

Рассмотрим полиномы , где - полином Лежандра. Т.к. степени этих полиномов не превышают 2n-1, то на основании системы (8.15) для них должны быть справедлива формула (8.14) и .

С другой стороны, в силу свойства ортогональности полиномов Лежандра выполнены неравенства:

при ,

поэтому

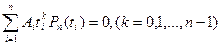(8.16).

Равенства (8.16) будут обеспечены при любых значениях , если положить , т.е. для достижения наивысшей точности квадратурной формулы (8.14) в качестве точек достаточно взять нули соответствующего полинома Лежандра. Как известно, из свойства 3, эти нули действительны, различны и расположены на интервале . Зная абсциссы , легко можно найти из линейной системы первых n уравнений системы (8.15) коэффициенты А_i (i = 1, 2, …, n). Определитель этой подсистемы есть определитель Вандермонда

 

и, следовательно, определяются однозначно.

Формула (8.14), где - нули полинома Лежандра и определяются из системы (8.15), называется квадратурной формулой Гаусса.

Рассмотрим теперь использование квадратурной формулы Гаусса для вычисления общего интеграла . Делая замену переменной , получим . Применяя к последнему интегралу, квадратурную формулу Гаусса получим:

, (8.16)

где , - нули полинома Лежандра , т.е. .

Остаточный член формулы Гаусса (8.16) с n узлами выражается следующим образом:

.

Отсюда получаем:

,

 

,

 

,

 

,

 

.

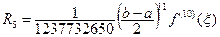Выведем квадратурную формулу Гаусса для случая трех ординат. Полином Лежандра третьей степени есть

.

Приравнивая этот полином нулю, находим:

, , .

Для определения коэффициентов в силу системы (8.15) имеем:

Отсюда: , .

Следовательно, .

Таблица 8.2

Элементы формулы Гаусса

n	t	ti	Ai
	1;2	±0.57735027
	1;3	±0.77459667	0.55555556 0.88888889
	4;1 3;2	±0.86113631 ±0.33998104	0.34785484 0.65214516
	5;1 4;2	±0.90617985 ±0.53846931	0.23692688 0.47862868 0.56888889
	6;1 5;2 4;3	±0.93246951 ±0.66120939 ±0.23861919	0.17132450 0.36076158 0.46791394
	7;1 6;2 5;3	±0.94910791 ±0.74153119 ±0.40584515	0.12948496 0.27970540 0.38183006 0.41795918

Пример 8.4 Вычислить интеграл из примера 8.3. по формуле Гаусса для четырех и для пяти точек. Оценить точность вычислений.

 

Метод Гаусса для 4 точек

 

 

 

 

 

 

 

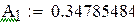
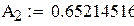
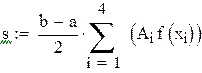
Метод Гаусса для 5 точек

 

 

 

 

 

 

 

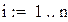
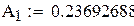
В ответе сохраняем шесть верных знаков.

Ответ: 0,423195

Рис. 8.4. Решение примера 8.3 в Mathcad