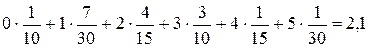Пусть задан закон распределения дискретной случайной величины Х.
| Х
| х 1
| х 2
| х 3
| ¼
| хn
|
| P
| p 1
| p 2
| p 3
| ¼
| pn
|
Математическое ожидание ЕХ (или Е(Х)) случайной величины Х определяется формулой
ЕХ = 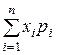
Замечание 21.1. В английском языке математическое ожидание звучит как m athematical e xpectation. Отсюда две традиции обозначения этого понятия – по первой букве первого или второго слова, соответственно МХ или ЕХ. Мы будем придерживаться второго варианта.
Рассмотрим отвлеченный пример. Мы уже говорили о связи понятия вероятности и частоты (статистическое определение вероятности), поэтому рассмотрим поясняющую «жизненную» ситуацию.
Пусть в некотором магазине, торгующем электробытовой техникой, получены статистические данные о числе проданных холодильников в каждый день месяца (условно считаем, что месяц состоит из 30 рабочих дней). Эти данные собраны в таблицу
| Количество проданных холодильников
|
|
|
|
|
|
|
| Число дней, в которые было продано столько холодильников
|
|
|
|
|
|
|
По этой таблице легко подсчитать число холодильников, проданных в магазине за месяц: 0×3+1×7+2×8+3×9+4×2+5×1 = 63. Чтобы подсчитать среднее число холодильников, продававшихся в один день месяца, нужно эту сумму разделить на 30, в результате получим 2,1. Если в приведенной таблице каждое число второй строки поделить на 30, то получится последовательность дробей
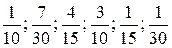 ,
,
каждая из которых представляет собой так называемую относительную частоту, с которой в данный месяц появлялся приведенный в верхней строке объём продаж. Очевидно, что если просуммировать все произведения чисел, стоящих в первой строке таблицы, на их относительные частоты, то получится то же среднее число продававшихся в один день холодильников:
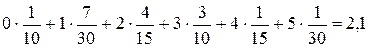
Если бы в последней формуле относительные частоты рассчитывались не для одного месяца, а для существенно большего срока, то при некоторых условиях (например, при отсутствии кризисных явлений, существенно влияющих на спрос населения на дорогостоящие товары) эти относительные частоты можно было бы считать довольно близкими к вероятностям соответствующих значений объёма продаж. Таким образом, приходим к выводу, что математическое ожидание случайной величины – это в некотором смысле её среднее значение.
Замечание 21.2. Первые эксперименты в теории вероятностей касались очень простых ситуаций – бросания монеты или кубика (кости), то есть случаев равновероятных исходов (описываемых равномерным дискретным распределением). Очевидно, что для такого распределения математическое ожидание совпадает со средним (арифметическим) значений случайной величины
Замечание 21.3. Хотя математическое ожидание и принято называть средним (значением) случайной величины, оно, кроме случаев равномерного распределения, совсем не обязано совпадать со средним арифметическим ее значений.
Замечании 21.4. Следует отметить, что случайная величина может вообще не принимать значения, равного её математическому ожиданию. Так, например, случайная величина, принимающая только значения 1 и –1, каждое – с вероятностью 0,5, имеет математическое ожидание, равное нулю.
Замечание 21.5. Более того, случайная величина может вообще не иметь конечного математического ожидания. Примером может служить одно из абсолютно непрерывных распределений – распределение Коши с плотностью
r(х) = 1/p (1+ x2). Забегая вперед скажем, что это распределение не имеет также ни дисперсии ни моментов.
Пример 21.2. Найти математическое ожидание случайной величины, заданной законом распределения
Здесь p + q = 1.
ЕХ = 1×р + 0×q = р
Замечание 21.6. Вернемся к нашей аналогии распределения вероятностей как точечных масс при обсуждении дискретного закона распределения. Точка, в которой нужно установить упор (подвес), для того, чтобы уравновесить стержень с «шариками-массами» (вероятностями) и будет точкой математического ожидания в данном случае. Так что мы можем говорить о математическом ожидании как о «средневзвешенном» значении.



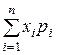
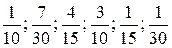 ,
,