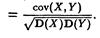Характеристикой зависимости между случайными величинами X и Y служит математическое ожидание произведения отклонений X и Y от их центров распределений (так иногда называют математическое ожидание случайной величины), которое называется коэффициентом ковариации или просто ковариацией.
Cov(X;Y) = E ((X– EX)(Y– EY))
Пусть X = { x 1, x 2, x 3,¼, xn }, Y= { y 1, y 2, y 3,¼, yn }. Тогда
Cov(X;Y)= 
Эту формулу можно интерпретировать так. Если при больших значениях Х более вероятны большие значения Y, а при малых значениях X более вероятны малые значения Y, то в правой части формулы ковариации положительные слагаемые доминируют, и ковариация принимает положительные значения.
Если же более вероятны произведения (xi – EX)(yj – EY), состоящие из сомножителей разного знака, то есть исходы случайного эксперимента, приводящие к большим значениям X в основном приводят к малым значениям Y и наоборот, то ковариация принимает большие по модулю отрицательные значения.
В первом случае принято говорить о прямой связи: с ростом X случайная величина Y имеет тенденцию к возрастанию.
Во втором случае говорят об обратной связи: с ростом X случайная величина Y имеет тенденцию к уменьшению или падению.
Если примерно одинаковый вклад в сумму дают и положительные и отрицательные произведения (xi – EX)(yj – EY) pij, то можно сказать, что в сумме они будут “гасить” друг друга и ковариация будет близка к нулю. В этом случае не просматривается зависимость одной случайной величины от другой.
Легко показать, что если
P ((X = xi)∩(Y = yj)) = P (X = xi) P (Y = yj) (i = 1,2,¼, n; j = 1,2,¼, k),
то cov(X;Y)= 0.
Действительно из (2) следует



Здесь использовано очень важное свойство математического ожидания: математическое ожидание отклонения случайной величины от ее математического ожидания равно нулю.
Ковариацию удобно представлять в виде
Cov(X;Y)=E(XY–XEY–YEX+EXEY)=E(XY)–E(XEY)–E(YEX)+E(EXEY)=
=E(XY)–EXEY–EXEY+EXEY=E(XY)–EXEY
Ковариация двух случайных величин равна математическому ожиданию их произведения минус произведение математических ожиданий.
Поскольку для независимых случайных величин EXY = EXEY, то, очевидно, что для независимых случайных величин X и Y cov(X;Y)=0.
Определение 21.16. Случайные величины, ковариация которых равна нулю, называют некоррелированными.
!!! Замечание 21.13. Как было показано выше, из независимости случайных величин следует их некоррелированность, то есть равенство нулю корреляции. Обратное неверно! Рассмотрим соответствующий пример:
Пусть случайная величина Х имеет равномерное распределение на интервале (-1, 1), а случайная величина Y связана со случайной величиной Х функциональной зависимостью Y=X2. Покажем, что cov (X,Y)=0, хотя налицо функциональная зависимость.
Учитывая, что ЕХ=0 (середина интервала (-1,1)), получаем:
cov (X,Y)=EXY-EXEY=EX3 =

Итак, из некоррелированности случайных величин не следует их независимость.
Ковариация случайных величин отражает степень близости зависимости случайных величин к линейной, то есть, к зависимости вида Y=aX+b.
Определение 21.17. Рассмотрим теперь еще одну меру линейной зависимости – коэффициент корреляции случайных величин Х и Y r(X,Y) =
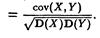
Может возникнуть вопрос, зачем вводить еще одну меру линейной зависимости?
1) Коэффициент корреляции меняется от -1 до 1, а не по всей числовой оси
2) Коэффициент корреляции, в отличие от ковариации, нечувствителен к смене единиц измерения
3) Если случайные величины независимы, то коэффициент корреляции, как и ковариация, равен нулю.
4) Если случайные величины линейно зависимы, то r=1 – прямая зависимость, r=-1, обратная. И наоборот, из равенства по модулю 1 следует линейная зависимость.
Пусть распределение случайных величин задано таблицей

ЕХ1 
ЕХ2 
DX1 = EX1 2 – (EX1)2= 0,59
DX2 = EX2 2 – (EX2)2= 0,2475
Cov (X1,X2)= E (X1,X2)–E X1 EX2
E (X1,X2) =


Замечание 21.14. Ковариационная и корреляционная матрицы – это таблицы, состоящие соответственно из ковариаций и коэффициентов корреляций соответствующих случайных величин. (Заметим, что по главной диагонали корреляционной матрицы стоят 1 – случайная величина, очевидно, находится сама с собой в линейной зависимости). Используются эти матрицы для наглядного представления данных о связи величин и в статистике.