

Семя – орган полового размножения и расселения растений: наружи у семян имеется плотный покров – кожура...

Эмиссия газов от очистных сооружений канализации: В последние годы внимание мирового сообщества сосредоточено на экологических проблемах...

Семя – орган полового размножения и расселения растений: наружи у семян имеется плотный покров – кожура...

Эмиссия газов от очистных сооружений канализации: В последние годы внимание мирового сообщества сосредоточено на экологических проблемах...
Топ:
Особенности труда и отдыха в условиях низких температур: К работам при низких температурах на открытом воздухе и в не отапливаемых помещениях допускаются лица не моложе 18 лет, прошедшие...
Эволюция кровеносной системы позвоночных животных: Биологическая эволюция – необратимый процесс исторического развития живой природы...
Определение места расположения распределительного центра: Фирма реализует продукцию на рынках сбыта и имеет постоянных поставщиков в разных регионах. Увеличение объема продаж...
Интересное:
Распространение рака на другие отдаленные от желудка органы: Характерных симптомов рака желудка не существует. Выраженные симптомы появляются, когда опухоль...
Средства для ингаляционного наркоза: Наркоз наступает в результате вдыхания (ингаляции) средств, которое осуществляют или с помощью маски...
Финансовый рынок и его значение в управлении денежными потоками на современном этапе: любому предприятию для расширения производства и увеличения прибыли нужны...
Дисциплины:
|
из
5.00
|
Заказать работу |
Содержание книги
Поиск на нашем сайте
|
|
|
|
Основы финансово-экономических расчетов
Наращение и дисконтирование капитала по простым
И сложным процентам
Наращение капитала может осуществляться по одной из следующих схем.
Схема 1 Простых процентов:
 (1)
(1)
где 
 - наращенная стоимость капитала;
- наращенная стоимость капитала;
 - современная стоимость (стартовая сумма) капитала;
- современная стоимость (стартовая сумма) капитала;
 - постоянная процентная ставка, действующая в пределах всего срока помещения капитала;
- постоянная процентная ставка, действующая в пределах всего срока помещения капитала;
 - срок помещения капитала;
- срок помещения капитала;
 - переменная процентная ставка, действующая в пределах периода времени
- переменная процентная ставка, действующая в пределах периода времени  ,
,  .
.
Схема 2 Сложных процентов:
 (2)
(2)
где  - эффективная годовая процентная ставка (проценты начисляются в конце года);
- эффективная годовая процентная ставка (проценты начисляются в конце года);
 - номинальная годовая процентная ставка (проценты начисляются несколько раз в пределах каждого года, например, ежеквартально);
- номинальная годовая процентная ставка (проценты начисляются несколько раз в пределах каждого года, например, ежеквартально);
 - периодичность начисления процентов в пределах года (например, при ежеквартальном начислении процентов – 4 раза).
- периодичность начисления процентов в пределах года (например, при ежеквартальном начислении процентов – 4 раза).
Одним из базовых понятий наращения капитала является его множитель наращения, рассчитываемый по формуле:
- для простых процентов:
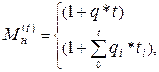 (3)
(3)
- для сложных процентов:
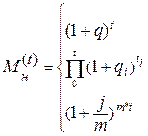 , (4)
, (4)
где 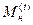 - множитель наращения капитала за перид
- множитель наращения капитала за перид 
Эквивалентность процентных ставок определяется из равенства множителей наращения капитала.
Эквивалентность простых и сложных процентных ставок:
- если известна сложная эффективная процентная ставка, то эквивалентную ей простую процентную ставку можно определить по формуле (5):
 , (5)
, (5)
- если известна сложная номинальная процентная ставка, то эквивалентную ей простую процентную ставку можно определить по формуле (6):

 , (6)
, (6)
- если известна простая процентная ставка, то эквивалентную ей сложную эффективную ставку можно определить по формуле (7):
|
|
 , (7)
, (7)
- если известна простая процентная ставка, то эквивалентную ей сложную номинальную процентную ставку можно определить по формуле (8):
 . (8)
. (8)
Эквивалентность номинальной и эффективной процентных ставок:
- если известна номинальная процентная ставка, то эквивалентная ей эффективная процентная ставка, которая отражает действительную годовую доходность от начисления процентов  раз в год по ставке
раз в год по ставке  % годовых, можно определить по формуле (9):
% годовых, можно определить по формуле (9):
 , (9)
, (9)
- если известна эффективная процентная ставка, то эквивалентная ей номинальная процентная ставка с заданной частотой их начисления в течение года можно определить по формуле (10):
 . (10)
. (10)
Математическое дисконтирование является процессом, обратным наращению капитала.
Общая формула дисконтирования капитала имеет вид:
 , (11)
, (11)
где  - коэффициент дисконтирования, который может быть исчислен одним из следующих способов:
- коэффициент дисконтирования, который может быть исчислен одним из следующих способов:
 (12)
(12)
Коэффициент дисконтирования является величиной, обратной множителю наращения капитала.
На основе формул наращения и дисконтирования капитала можно рассчитать любой из параметров:
- размер процентной ставки;
- срок помещения капитала.
|
|
|

Наброски и зарисовки растений, плодов, цветов: Освоить конструктивное построение структуры дерева через зарисовки отдельных деревьев, группы деревьев...

История развития хранилищ для нефти: Первые склады нефти появились в XVII веке. Они представляли собой землянные ямы-амбара глубиной 4…5 м...

Опора деревянной одностоечной и способы укрепление угловых опор: Опоры ВЛ - конструкции, предназначенные для поддерживания проводов на необходимой высоте над землей, водой...

Индивидуальные и групповые автопоилки: для животных. Схемы и конструкции...
© cyberpedia.su 2017-2024 - Не является автором материалов. Исключительное право сохранено за автором текста.
Если вы не хотите, чтобы данный материал был у нас на сайте, перейдите по ссылке: Нарушение авторских прав. Мы поможем в написании вашей работы!