

История создания датчика движения: Первый прибор для обнаружения движения был изобретен немецким физиком Генрихом Герцем...

Общие условия выбора системы дренажа: Система дренажа выбирается в зависимости от характера защищаемого...

История создания датчика движения: Первый прибор для обнаружения движения был изобретен немецким физиком Генрихом Герцем...

Общие условия выбора системы дренажа: Система дренажа выбирается в зависимости от характера защищаемого...
Топ:
Теоретическая значимость работы: Описание теоретической значимости (ценности) результатов исследования должно присутствовать во введении...
Определение места расположения распределительного центра: Фирма реализует продукцию на рынках сбыта и имеет постоянных поставщиков в разных регионах. Увеличение объема продаж...
Методика измерений сопротивления растеканию тока анодного заземления: Анодный заземлитель (анод) – проводник, погруженный в электролитическую среду (грунт, раствор электролита) и подключенный к положительному...
Интересное:
Инженерная защита территорий, зданий и сооружений от опасных геологических процессов: Изучение оползневых явлений, оценка устойчивости склонов и проектирование противооползневых сооружений — актуальнейшие задачи, стоящие перед отечественными...
Аура как энергетическое поле: многослойную ауру человека можно представить себе подобным...
Как мы говорим и как мы слушаем: общение можно сравнить с огромным зонтиком, под которым скрыто все...
Дисциплины:
|
из
5.00
|
Заказать работу |
|
|
|
|
х ′′ (τ) + х ′ (τ) = τ + 1, х (0) = 1 , х ′ (0) = 0 , (*)
так как значению t = 1 отвечает значение τ = 0.
Пусть х (τ) ≓ Х (p), тогда операторное уравнение для уравнения (*) запишется в виде:
р2 Х (p) – р + р Х (p) - 1 =  .
.
Решая его относительно Х (p), найдем: Х (p) = 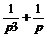 . Следовательно, х (τ) =
. Следовательно, х (τ) = 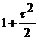 . Заменив τ на t - 1, получим искомое решение задачи Коши: х (t) =
. Заменив τ на t - 1, получим искомое решение задачи Коши: х (t) = 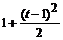 .
.
Пример 6.5. Найти общий интеграл дифференциального уравнения x ′′ + 2 x ′ + 10 x = 2 е - t cos 3 t.
Решение. Для получения общего интеграла возьмем произвольные начальные условия
х (0) = с 0и х' (0) = с 1.
Перейдем к уравнению в изображениях:
р2 Х (p) – с 0 р - с 1 + 2 р Х (p) -2 с 0 + 10 Х (p) = 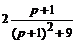 ,
,
откуда
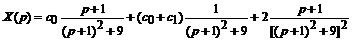
Выполнив обращение, получим искомое решение
х(t) = e - t [ c 0 cos 3 t + 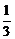 (t + c 1) sin 3 t ],
(t + c 1) sin 3 t ],
где c 1 = c 0 + c 1 - новая произвольная постоянная.
Пример. 6.6. Найти решение уравнения x ′ + 3 x = f (t),
удовлетворяющее условию х (0) = 0,если
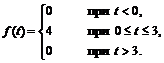
Решение. Пусть x (t) ≓ Х (p). Используя теорему запаздывания, представим функцию f (t) в следующем виде:
f (t) = 4 η (t) – 4 η (t -3).
Переходим к уравнению в изображениях:
р Х (p) +3 Х (p) = 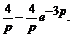 Находим операторное решение заданного уравнения:
Находим операторное решение заданного уравнения:  .
.
Так как 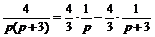 ≒
≒ 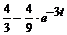 ,
,
то выполнив обращение (применив теорему запаздывания), получим искомое решение: 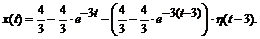
6.2. Р е ш е н и е з а д а ч и К о ш и д л я с и с т е м
у р а в н е н и й
Решение систем линейных дифференциальных уравнений с постоянными коэффициентами операционным методом производится по той же схеме, что и решение одного дифференциального уравнения.
|
|
Рассмотрим для простоты систему дифференциальных уравнений второго порядка. (Общий случай решения задачи Коши для системы п –ого порядка принципиально ничем не отличается от случая п = 2).
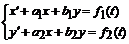 , (6.6)
, (6.6)
где а 1, a 2, b 1, b 2 = const. Требуется найти решение системы (6.6), удовлетворяющее начальным условиям:
х (0) = x 0и y (0) = y 0, где x 0, y 0 - заданные числа.
. Будем предполагать, что искомые функции x (t) и y (t), все рассматриваемые производные, а также функции f 1 (t) и f 2 (t) являются оригиналами.
Обозначим: x (t) ≓ Х (p); y (t) ≓ Y (p); f 1 (t) ≓ F 1 (p) и f 2 (t) ≓ F 2 (p).
Преобразуем по Лапласу каждое из уравнений заданной системы – перейдем к операторной системе:
 , (6.7)
, (6.7)
Решая (6.7) как линейную алгебраическую систему относительно Х(p) и Y (p), найдем Х(p) и Y (p), а затем, выполнив обращение, и искомые функции x (t) и y (t).
Пример. 6.7. Решить задачу Коши:
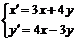 , x (0) = у (0)= 1.
, x (0) = у (0)= 1.
Решение. Пусть x (t) ≓ Х (p) и у(t) ≓ У(p). Перейдем от оригиналов к изображениям:
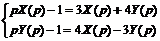 .
.
Разрешая полученную систему относительно Х (p) и У(p), найдем операторное решение заданной системы:
Х (p) = 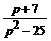 , У (p) =
, У (p) = 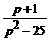 .
.
Восстановим оригиналы для Х (p) и У (p) - получим искомое решение: x (t) =  , y (t)= ch 5 t +
, y (t)= ch 5 t +  sh 5 t.
sh 5 t.
Пример. 6.8. Решить систему уравнений: 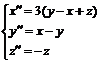 ,
,
х (0) = х' (0) = 0, y (0) = 0, y ' (0) = -1, z (0) = 1, z ' (0) = 0.
Решение. Обозначим: x (t) ≓ Х (p), у(t) ≓ У(p) и z (t) ≓ Z (p) и перейдем к операторной системе:
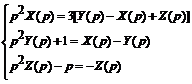 ,
,
Из полученной системы находим операторное решение системы:
Х (p) = 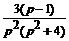 , У(p) =
, У(p) = 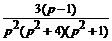 -
- 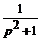 , Z (p)=
, Z (p)=  .
.
Выполнив обращение, получим искомое решение системы:
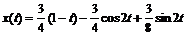 , z (t)= с os t,
, z (t)= с os t,
 .
.
7. Применение интеграла Дюамеля для решения обыкновенных линейных дифференциальных уравнений с постоянными коэффициентами
При исследовании систем автоматического управления часто возникает задача интегрирования нескольких линейных дифференциальных уравнений с одинаковыми левыми и различными правыми частями. В этом случае применение интеграла Дюамеля для интегрирования дифференциальных уравнений особенно выгодно: значительно сокращается объем вычислительной работы.
|
|
Итак, пусть имеется линейное дифференциальное уравнение с постоянными коэффициентами (для простоты рассмотрим уравнение второго порядка)
x '' + a 1 x ' + a 2 x = f(t), (7.1)
где a 1 , a 2 = const. Будем предполагать, что искомая функция x (t), все ее рассматриваемые производные, а также функция f (t) являются оригиналами.
Требуется найти решение уравнения (7.1), удовлетворяющее начальным условиям: х (0) = х 1 и х' (0) = х 2, где х1 и х 2 – заданные числа.
При решении поставленной задачи с помощью интеграла Дюамеля различают д в а с л у ч а я н а ч а л ь н ы х у с л о в и й:
нулевые начальные условия (х1= х2 = 0) и когда хотя бы одно из чисел - х 1 или х 2, не равно нулю.
П е р в ы й с л у ч а й: заданы н у л е в ы е начальные условия: х (0) = х' (0) = 0.
При таких начальных условиях поступают следующим образом.
1.Записывают вспомогательное уравнение, левая часть которого совпадает с левой частью данного уравнения (7.1), а в правой части – единичная функция Хевисайда η (t):
z'' + a 1 z' + a 2 z = η (t). (7.2)
2. Операционным методом находят его частное решение z (t), удовлетворяющее н у л е в ы м начальным условия
z (0) = z ' (0) = 0.
3. Записывают с помощью интеграла Дюамеля по формуле (7.3) или (7.4) в виде квадратуры искомое решение x (t) задачи Коши:
x (t) =  , (7.3)
, (7.3)
x (t) = f (0) z (t) + 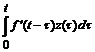 . (7.4)
. (7.4)
В т о р о й с л у ч а й: заданы н е н у л е в ы е начальные условия:
х (0) = x 0 и х' (0) = х1 ,
причем хотя бы одно из чисел- x 0или х 1, не равно нулю.
В этом случае н е о б х о д и м о сделать замену искомой функции x (t) таким образом, чтобы задача свелась к задаче с нулевыми начальными условиями (к случаю 1).
Например (см. также пример 7.2), пусть требуется найти решение дифференциального уравнения (7.1)
x '' + a 1 x ' + a 2 x = f (t),
удовлетворяющее ненулевым начальным условиям:
х (0) = x 0и х' (0) = х 1 .
Положим
y (t) = x (t) - x 0 - х 1 t. (7.5)
|
|
Тогда y′ (t) = x′ (t) - х 1, y′′ (t) = x′′ (t),
|
|
|

Поперечные профили набережных и береговой полосы: На городских территориях берегоукрепление проектируют с учетом технических и экономических требований, но особое значение придают эстетическим...

Автоматическое растормаживание колес: Тормозные устройства колес предназначены для уменьшения длины пробега и улучшения маневрирования ВС при...

Индивидуальные очистные сооружения: К классу индивидуальных очистных сооружений относят сооружения, пропускная способность которых...

Особенности сооружения опор в сложных условиях: Сооружение ВЛ в районах с суровыми климатическими и тяжелыми геологическими условиями...
© cyberpedia.su 2017-2024 - Не является автором материалов. Исключительное право сохранено за автором текста.
Если вы не хотите, чтобы данный материал был у нас на сайте, перейдите по ссылке: Нарушение авторских прав. Мы поможем в написании вашей работы!