ДЛЯ НАХОЖДЕНИЯ ИЗОБРАЖЕНИЙ РАЗРЫВНЫХ ФУНКЦИЙ (ИМПУЛЬСОВ).
Пустьзадана некоторая функция φ(t), график которой представлен на рис. 4.1. При умножении этой функции φ(t) на функцию Хевисайдаполучается функция-оригинал:
 (4.1)
(4.1)
т.е. в результате умножения произошло обнуление значений заданной функции φ (t) при t < 0 (рис.4.2).

| 
|
| Рис. 4.1.
| Рис.4.2.
|
Рассмотрим теперь функцию - оригинал f (t), график которой представлен на рис. 4.3. Тогда функция
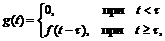 (4.2)
(4.2)
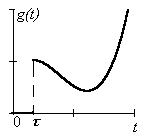
где τ – положительное число, имеет график (рис.4.4), который получается из графика f (t) сдвигом последнего на величину τ вдоль оси t. Таким образом, если функция f (t) определяет течение во времени некоторого процесса, то функция g (t) определяет тот же процесс, но начавшийся с опозданием τ. 

| 
|
| Рис. 4.3.
| Рис.4.4.
|
С помощью единичной функции Хевисайда запаздывающую на τ функцию g (t) (4.2) можно записать в виде:
g (t) = h (t - τ) ·f (t – τ), (4.3)
так как h (t - τ) = 0 при t < τ (в этом случае аргумент отрицателен) и 1 при t ≥ τ.
При нахождении изображения оригинала в случае, когда его аргумент запаздывает, используется т е о р е м а з а п а з д ы в а н и я: если f (t) ←÷ F (p), то запаздывание аргумента оригинала на τ > 0 приводит к умножению изображения оригинала без запаздывания на
е - рτ, т. е.
h (t - τ) f (t – τ) ≓ е - рτ F (p). (4.4)
Пример 4.1. Найти изображение оригинала f (t)= е t - 2 h (t - 2 ).
Решение. Здесь f (t) есть функция е t, но включаемая с «запаздыванием» τ = 2. Так как е t ≓  , то по теореме запаздывания (4.4) имеем: е t - 2 h (t - 2 ) ≓
, то по теореме запаздывания (4.4) имеем: е t - 2 h (t - 2 ) ≓  .
.
З а м е ч а н и е. Если в записи f (t) опустить множитель h (t - 2 ), то получится функция е t – 2, которая означает оригинал е t - 2 h (t) без запаздывания смотри формулу (4.1)). Изображением этого оригинала будет:
е t - 2 h (t) = е – 2· е t h (t) ≓ 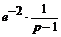 .
.
Таким образом, н е д о п у с т и м о опускать множители вида h (t - τ) в записи функций (см. также пример 3.5).

| 
|
| Рис. 4.5.
| Рис.4.6.
|
Пример 4.2. Найти изображение функций f 1 (t) и f 2 (t), представленных соответственно на рис. 4.5 и 4.6.
Решение. Первая функция f 1 (t) есть импульс величины 4, «включаемый» в момент t = 0 и «погашаемый» в момент τ = 2; следовательно, согласно (4.3) запишем: f 1 (t)= 4· h (t) - 4· h (t - 2).
Аналитическое выражение функции f 2 (t) найдем, рассуждая следующим образом: в момент t = 0 появился импульс величины 2 - запишем: f 2 (t) = 2· h(t).
Затем в момент τ = 1 импульс увеличился на 2:
f 2 (t) = 2· h(t) + 2· h (t - 1 ).
Получившийся импульс в момент τ = 2 уменьшился на 3:
f 2 (t) = 2 · h(t) + 2· h (t - 1 ) - 3· h (t - 2).
Далее в момент τ = 3 исследуемый импульс, уменьшившись на 1, стал равным 0 (исчез); т.е. окончательное выражение для f 2 (t) запишется в виде:
f 2 (t) = 2 · h(t) + 2· h (t - 1) - 3· h (t - 2 ) -1· h (t - 3).
Применяя теорему запаздывания(4.4), находим:
f 1 (t) ≓  -
-  =
=  .
.
f 2 (t) ≓ 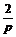 +
+  -
-  -
-  .
.
З а м е ч а н и е. В рассматриваемом примере импульс имел
п р я м о у г о л ь н у ю форму, поэтому удобно было в момент изменения его формы сразу «гасить» или «увеличивать» его на наблюдаемую величину. В случае импульса более сложной формы при нахождении его аналитического описания удобнее в момент изменения формы «гасить» его до нуля и сразу «включать» импульс требуемой формы (см. примеры 4.3 и 4.4).
Пример 4.3. Построить график функции
f (t)= (t 2 - 6 t + 11)· h (t – 2) и найти ее изображение.
Решение. Функция f (t) описывает некоторый процесс φ(t), «включаемый» с запаздыванием τ = 2. Для того, чтобы решить, какой это процесс, нужно представить заданную функцию в форме:
f (t) = φ (t - 2) 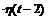 .
.
Сделаем это:
f (t)= (t 2 - 6 t + 11)· h (t – 2) =[(t – 2)2 + 4 t – 4 - 6 t + 11]· h (t – 2) =
=[(t – 2)2 – 2 t + 7)]· h (t – 2) = [(t – 2)2 – 2(t - 2)+ 3)]· h (t – 2).
Отсюда следует, что f (t) есть процесс φ(t) = t 2 – 2 t + 3, «включаемый» с запаздыванием τ = 2. На рис.4.7 представлены графики функций f (t) и φ(t). Так как
φ(t) = t 2 – 2 t + 3 ≓  -
-  +
+  ,
,
то применяя теорему запаздывания, находим:
f(t) = φ (t - 2 ) 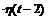 ≓ (
≓ ( -
-  +
+  )
) 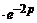 .
.

| 
|
| Рис. 4.7.
| Рис.4.8.
|
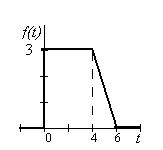
Пример 4.4. Найти изображение функций f (t), представленной на рис. 4.8.
Решение. Запишем заданную функцию в аналитическом виде:
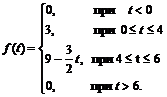
С помощью единичной функции Хевисайда запишем f (t) одним аналитическим выражением:
В момент t = 0 «включается» функция, равная 3, следовательно, f (t) = 3 · h (t).
В момент τ = 4 функция, равная 3, «гасится» и «включается» функция  : f (t) = 3 · h (t) - 3 · h (t - 4) +
: f (t) = 3 · h (t) - 3 · h (t - 4) +  .
.
В момент τ = 6 функция  «гасится» (сигнал исчез), следовательно, искомое выражение функции имеет вид:
«гасится» (сигнал исчез), следовательно, искомое выражение функции имеет вид:
f(t) = 3 · h (t) - 3 · h (t - 4) +  -
- 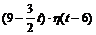
или f(t) = 3 · h (t) +  -
- 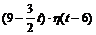 .
.
Чтобы найти изображение этой функции, нужно представить ее в следующей форме (см. также пример 4.3):
f (t) = 3 · h (t) + φ 1(t - 4) 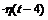 - φ2(t - 6 )
- φ2(t - 6 )  .
.
Выполним следующие преобразования:
f (t) = 3 · h (t) + [ 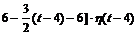 -
-  =
=
= 3 · h (t) 
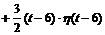 .
.
Так как
φ1(t)= 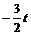 ≓
≓ 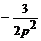 и φ 2(t - 6) =
и φ 2(t - 6) =  ←÷
←÷ 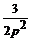 ,
,
то, применяя теорему запаздывания (4.4), находим:
f (t) ≓ 
 +
+  .
.
Пример 4.5. Найти оригинал по его изображению:
а) F (p)= 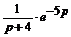 ; б) F (p)=
; б) F (p)=  .
.
Решение. а) учитывая, что  ≒
≒  , по теореме запаздывания (4.4) находим:
, по теореме запаздывания (4.4) находим: 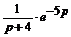 ≒
≒ 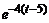
 .
.
б) так как  ≒
≒ 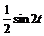 , применим (4.4) и получим:
, применим (4.4) и получим:
 ≒
≒ 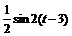
 .
.
ВОССТАНОВЛЕНИЕ ОРИГИНАЛА
ПО ИЗОБРАЖЕНИЮ
В операционном исчислении обратная задача - определение оригинала f (t) по известному изображению F (p), является одной из главных.
Важным частным случаем изображений являются изображения F (p) в виде правильных (m < n) и неправильных (если m ≥ n) рациональных дробей:
 , (5.1)
, (5.1)
где Qm (p) и Rn (p) - многочлены от р степени m и n соответственно.
Неправильность дроби указывает, что оригинал будет содержать дельта функцию Дирака δ(t) или ее производные.
Во многих случаях заданное изображение можно преобразовать к такому виду, когда оригинал легко восстанавливается непосредственно с помощью свойств преобразования Лапласа и таблицы изображений. Иногда задачу удается решить с помощью теоремы об изображении свертки.
Изображения F (p) в виде неправильной рациональной дроби, удобно п р е д в а р и т е л ь н о п р е о б р а з о в а т ь: выделить в этой дроби, разделив числитель на знаменатель (по правилу деления многочленов «уголком»), целую часть – многочлен Mm - n (p) степени
m - n, и некоторую правильную дробь 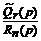 :
:

где Q ̃ r (p) - многочлен степени r, причем r < n.
П р и о б р а щ е н и и изображения в виде многочлена используетсясвойство линейности изображения и соответствие:
р к ÷→ δ (к)(t) (к = 0,1,...)
П р и о б р а щ е н и и изображения в виде правильной рациональной дроби 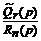 широко используется следующий прием: разлагают эту дробь в сумму простейших дробей методом неопределенных коэффициентов и находят оригиналы для каждой.
широко используется следующий прием: разлагают эту дробь в сумму простейших дробей методом неопределенных коэффициентов и находят оригиналы для каждой.
Пример 5.1. Найти оригинал f (t), если  .
.
Решение. П е р в ы й с п о с о б. Выделяя полный квадрат в знаменателе и далее, используя табличное изображение (10), получим:
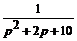 =
= 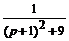 =
=  ≒
≒ 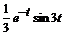 .
.
В т о р о й с п о с о б. Раскладывая дробь в сумму простейших, используя изображение для е at, получим
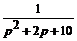 =
=  -
- 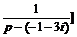 ≒
≒
≒  =
= 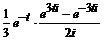 =
= 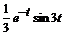 .
.
Пример 5.2. Найти оригинал f (t), если  .
.
Решение. П е р в ы й с п о с о б. Используем теорему Бореля об изображении свертки, получим
 =
= 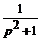 ·
· 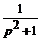 ≒
≒  *
*  =
=  =
=
= 
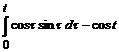
 =
= 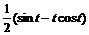 .
.
В т о р о й с п о с о б. Раскладывая дробь в сумму простейших, используя изображение для е at, получим
 =
= 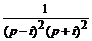 =
= 
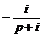 +
+ 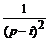 +
+  ÷→
÷→
≒ 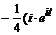
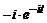 +
+  +
+ 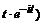 =
= 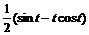 .
.
Пример 5.3. Найти оригинал f (t), если 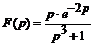 .
.
Решение. Найдем сначала оригинал для дроби 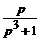 , разложив ее в сумму простейших:
, разложив ее в сумму простейших:
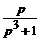 =
= 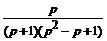 =
=  +
+ 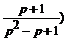 =
=
= 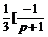 +
+  =
= 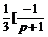 +
+  +
+ 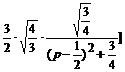
≒ 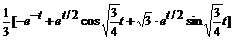 .
.
Учтем теперь сомножитель е –2 р : применив теорему запаздывания, найдем
 ≒
≒  .
.



 (4.1)
(4.1)

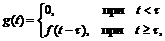 (4.2)
(4.2)


 , то по теореме запаздывания (4.4) имеем: е t - 2 h (t - 2 ) ≓
, то по теореме запаздывания (4.4) имеем: е t - 2 h (t - 2 ) ≓  .
.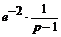 .
.

 -
-  =
=  .
.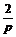 +
+  -
-  -
-  .
.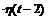 .
.  -
-  +
+  ,
, 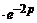 .
.

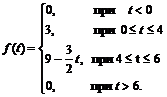
 : f (t) = 3 · h (t) - 3 · h (t - 4) +
: f (t) = 3 · h (t) - 3 · h (t - 4) +  .
.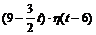
 -
- 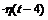 - φ2(t - 6 )
- φ2(t - 6 )  .
.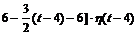 -
-  =
=
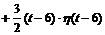 .
.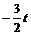 ≓
≓ 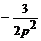 и φ 2(t - 6) =
и φ 2(t - 6) =  ←÷
←÷ 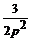 ,
, +
+  .
.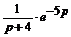 ; б) F (p)=
; б) F (p)=  .
.  ≒
≒  , по теореме запаздывания (4.4) находим:
, по теореме запаздывания (4.4) находим: 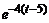
 .
. ≒
≒ 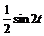 , применим (4.4) и получим:
, применим (4.4) и получим: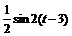
 .
. , (5.1)
, (5.1)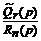 :
:
 .
.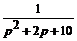 =
= 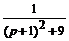 =
=  ≒
≒ 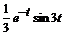 .
. -
- 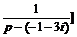 ≒
≒ =
= 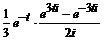 =
=  .
. =
= 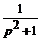 ·
·  *
*  =
=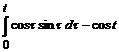
 =
= 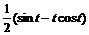 .
.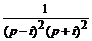 =
= 
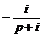 +
+ 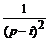 +
+  ÷→
÷→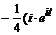
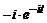 +
+  +
+ 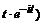 =
= 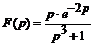 .
.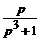 , разложив ее в сумму простейших:
, разложив ее в сумму простейших: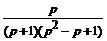 =
=  +
+ 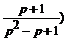 =
=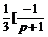 +
+  =
=  +
+ 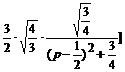
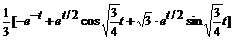 .
. ≒
≒  .
.

