И нитяной маятник — это шарик, подвешенный на нити, способный совершать колебательное движение.

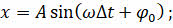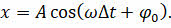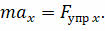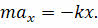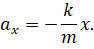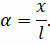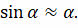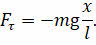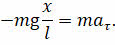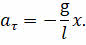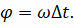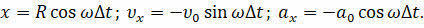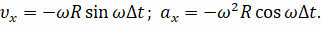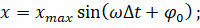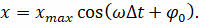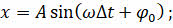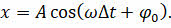
Колебания — это особая форма движения в том смысле, что различные по своей природе физические процессы описываются одинаковыми математическими зависимостями физических величин от времени.

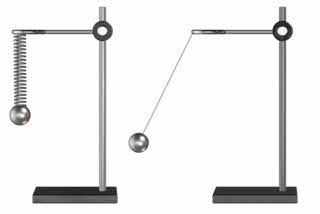
Рассмотрим процесс колебаний горизонтального пружинного маятника, в котором груз продет через тонкий металлический стержень, расположенный вдоль оси пружины. Для простоты, будем считать, что что сила трения между грузом и стержнем пренебрежимо мала. Вся система находится в равновесии, а внешние силы — сила тяжести и сила нормальной реакции стержня, уравновешивают друг друга.

Направим координатную ось параллельно стержню, а за начало отсчёта примем центр тяжести тела в положении равновесия.

Приложив внешнюю силу, выведем маятник из равновесия, немного растянув пружину. В пружине возникнет сила упругости, которая будет стремиться вернуть маятник в положение равновесия.

Если мы уберём воздействие внешней силы, то система придёт в движение и груз начнёт двигаться влево с некоторым ускорением, а сила упругости будет уменьшаться. Дойдя до положения равновесия сила упругости исчезнет, как и (согласно второму закону Ньютона), ускорение маятника. Но к этому моменту его скорость достигнет максимума и не останавливаясь по инерции груз продолжит движение вправо. Пружина начнёт сжиматься и в ней вновь возникнет сила упругости, но направленная уже вправо. Следовательно, возникнет и ускорение, направленное туда же, куда и сила упругости — против скорости движения маятника. Поэтому со временем маятник остановится в крайнем левом положении. Здесь действующая на маятник сила упругости принимает своё максимальное значение, как, впрочем, и ускорение. Поэтому маятник вновь придёт в движение и будет двигаться вправо, пройдя в обратном направлении через те же промежуточные положения. Дойдя до крайнего правого положения маятник совершит одно полное колебание. Если бы в нашей системе отсутствовали силы сопротивления, то такое движение маятника продолжалось бы бесконечно долго.

Получим уравнение движения нашего маятника. Для этого запишем уравнение движение груза под действием силы упругости вдоль оси икс:

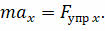
Из механики мы с вами знаем, что проекция силы упругости прямо пропорциональна смещению тела:

Перепишем второй закон Ньютона с учётом последней формулы:

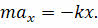
Выразив из полученного равенства ускорение груза, тем самым мы получим уравнение, описывающее колебание тела под действием силы упругости:

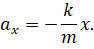
Данное выражение называют динамическим уравнением движения пружинного маятника.

И давайте ещё получим уравнение движение математического маятника — физической модели обычного нитяного маятника.

И так, пусть в момент начала наблюдения маятник находится в положении равновесия. В этой точке на него действуют всего две силы — сила упругости нити и сила тяжести точки, которые уравновешивают друг друга.

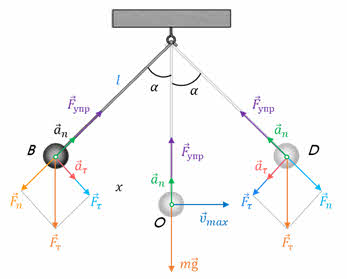
Приложив внешнюю силу, выведем маятник из равновесия и отпустим его. Теперь сила тяжести не может уравновесить силу упругости нити и в системе возникнет возвращающая сила, являющаяся тангенциальной составляющей силы тяжести. А её нормальная составляющая будет направлена вдоль нити против силы упругости. Она будет менять направление вектора скорости материальной точки.

Возвращающая сила будет сообщать материальной точке тангенциальное ускорение, и маятник начнёт двигаться по дуге окружности к положению равновесия с возрастающей по модулю скоростью. Чем ближе материальная точка подходит к положению равновесия, тем меньше становиться значение возвращающей силы и модуля ускорения. Однако при этом возрастает скорость точки. Дойдя до положения равновесия, возвращающая сила, а, следовательно, и тангенциальное ускорение точки обращаются в ноль. Но вот её скорость достигает максимума. Поэтому, не останавливаясь, маятник продолжает своё движение по дуге вверх по инерции. При этом вновь возникает возвращающая сила, которая становится тем больше, чем выше поднимается маятник. Но теперь эта сила направлена против движения маятника и постепенно уменьшает его скорость. Достигнув крайнего левого положения скорость маятника становится равной нулю, а возвращающая сила и ускорение достигают своего максимального значения.

Маятник на мгновение замирает, а затем начинает двигаться в обратном направлении, пройдя через те же промежуточные положения пока не достигнет исходной точки. А так как силы сопротивления отсутствуют, то после этого движение маятника будет повторяться в уже описанной последовательности

Теперь предположим, что в некоторый момент времени маятник находится в некоторой точке В, а его смещение от положения равновесия равно длине дуги ОВ. Пусть длина нити подвеса маятника равна l, а его масса m. Из рисунка видно, что значение возвращающей силы, можно найти как произведение модуля силы тяжести на синус угла альфа:

где α — это угол отклонения маятника от положения равновесия, равный отношению смещения маятника к длине нити подвеса:

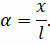
Ранее предполагалось, что углы отклонения нити маятника от вертикали могут быть любыми. В дальнейшем же мы будем считать их малыми. А при малых углах, если угол измерен в радианах, синус этого угла можно заменить его градусной мерой:

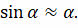
Перепишем уравнение для тангенциальной составляющей силы тяжести с учётом последнего равенства:

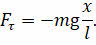
Обратите внимание на знак «минус» в этой формуле. Его здесь ставят потому, что тангенциальная составляющая силы тяжести направлена к положению равновесия, а смещение отсчитывают от положения равновесия.

Запишем второй закон Ньютона для нашего маятника, в проекциях на направление касательной к траектории его движения:

Теперь приравняем правые части последних двух равенств:

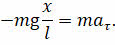
Сократив полученное выражение на массу маятника, приходим к тому, что тангенциальное ускорение математического маятника прямо пропорционально его смещению и направлено к положению равновесия:

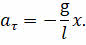
Эту формулу называют динамическим уравнением движения математического маятника. Оно имеет такой же вид, что и для пружинного маятника. Это означает, что движения обоих маятников происходят одинаковым образом и изменяются со временем по одному и тому же закону несмотря на то, что силы, вызывающие колебания, имеют разную физическую природу.

 

"Гармонические колебания."

Теперь зная, как связаны между собой ускорение и координата колеблющегося тела, можно найти зависимость координаты от времени. Для этого давайте с вами рассмотрим равномерное вращение материальной точки по окружности известного радиуса. Пусть рассматриваемое движение происходит против хода часовой стрелки. Выберем систему координат ХОY так, как это показано на рисунке.

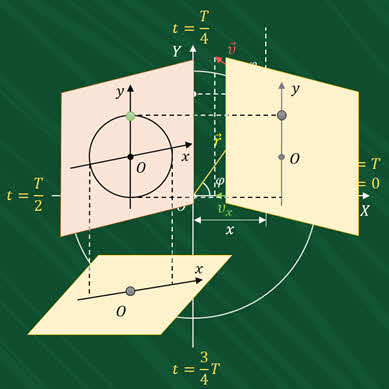
Теперь предположим, что через некоторый промежуток времени Δ t материальная точка повернулась на угол φ. Давайте вспомним, что придвижении по окружности материальная точка обладает линейной скоростью, направленной по касательной в каждой точке траектории, и центростремительным ускорением, направленным всегда по радиусу к центру окружности. Спроецируем на ось OX радиус-вектор движущейся точки, её линейную скорость и центростремительное ускорение.

Проекция радиус-вектора в положении «Эм» (М) (это точка В) является смещением материальной точки от центра окружности вдоль оси Ох. Следовательно, на выбранной оси этому смещению соответствует координата х точки В.

Поскольку при равномерном вращении точки по окружности её координата (смещение) будет периодически изменяться от x _min = – R до х _max = + R, то можно сказать, что точка В совершает колебательное движение вдоль оси Ох, а её координата х является координатой колеблющейся точки.

Соответственно будут изменяться и проекция линейной скорости (от + υ ₀ = ωR до – υ ₀ = – ωR) и проекция центростремительного ускорения материальной точки (от + a ₀ = ω ² R до– a ₀ = ω ² R).

Теперь вспомним, что угол поворота материальной точки при её движении по окружности можно найти, как произведение угловой скорости точки и времени поворота:

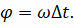
Так как при равномерном вращении по окружности линейная скорость направлена по касательной, а центростремительное ускорение — к центру окружности, то изменение координаты, проекции скорости и центростремительного ускорения материальной точки будут описываться уравнениями, которые вы сейчас видите на экране:

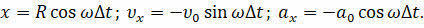
Перепишем данные уравнения, выразив начальную скорость и ускорение точки через угловую скорость:

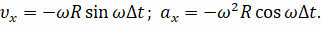
Поскольку функции синуса и косинуса являются периодическими, то через промежуток времени, равный периоду, все характеристики движения точки В вдоль оси Ох примут прежние значения, то есть значения характеристик периодически повторяются. А как мы говорили на прошлом уроке, повторяемость — это основной признак периодического движения.

Обратим внимание на то, что проекция ускорения точки B в любой момент времени пропорционально смещению и противоположно ей по знаку:

Перепишем это равенство так, как это показано на экране:

Колебания, описываемые полученным уравнением, называются гармоническими, а система, совершающая такие колебания, — гармонической колебательной системой, или гармоническим осциллятором.

Гармоническими колебаниями называются колебания, при которых смещение колеблющейся точки от положения равновесия изменяется с течением времени по закону синуса или косинуса:

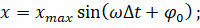
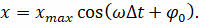
Термин «гармонические колебания» впервые был введён в науку швейцарским физиком Даниилом Бернулли.

В записанных уравнениях φ ₀ — это начальная фаза колебаний, которая определяет состояние колебательной системы в начальный момент времени.

x _max — это максимальное смещение материальной точки от положения устойчивого равновесия, называемое также амплитудой колебаний: