Введение
«Решение задач – практическое искусство, подобное
плаванию, катанию на лыжах или игре на фортепиано;
научиться ему можно, только подражая хорошим
образцам и постоянно практикуясь»
Д. Пойя
Увлечение математикой часто начинается с размышления над какой-то особенно понравившейся задачей. Я рассмотрел множество разных заданий, и такие как задачи на клетчатой бумаге.
Оказывается, задачи, связанные с бумагой в клеточку, достаточно разнообразны. Можно вычислять площади многоугольников, нарисованных на клетчатом листке, а раскраска клеточек помогает решать многие задачи.
Актуальность данного проекта заключается в том, что для упрощения решения и экономичности времени можно использовать формулу Пика, а решение таких задач, формирует вычислительные навыки, способствует развитию логического мышления и повышает интерес к изучению математики.
Цель работы:
- выяснить существует ли чёткая классификация и структурирование задач на клетчатой бумаге по методам и способам решения.
Задачи:
- рассмотреть задачи на нахождение площади многоугольника, задачи на разрезание,
на нахождение расстояния и игры на клетчатой бумаге;
-провести анализ работы и сформулировать вывод.
Объект исследования: задачи на клетчатой бумаге.
Предмет исследования: многообразие задач на клетчатой бумаге.
Методы исследования: сравнение, обобщение, аналогии, изучение литературных и Интернет-ресурсов, анализ и классификация информации.
Гипотеза: возможно непонимание учащимися задач на клетчатой бумаге объясняется отсутствием алгоритмов решения этих задач и необходимостью проявить творческий подход и смекалку. Предположим, что исследуя задачи на клетчатой бумаге, расширятся знания о геометрических фигурах и повысится интерес к изучению математики.
Теоретическая часть
Формула Пика
Георг Пик – австрийский математики. Он известен своей теоремой о вычислении площади многоугольника, которая появилась в его восьмистраничной работе 1899 года. Эта теорема оставалась незамеченной в течение некоторого времени после того, как Пик её опубликовал, однако в 1949 г. польский математик Гуго Штейнгауз включил теорему (или как её ещё называют — формулу) в свой знаменитый «Математический калейдоскоп». С этого времени теорема Пика стала широко известна. В Германии формула Пика включена в школьные учебники.
При решении задач на клетчатой бумаге необходимы понятия решетки и узла.
Клетчатая бумага (точнее — ее узлы), на которой мы часто предпочитаем рисовать и чертить, является одним из важнейших примеров точечной решетки на плоскости.
Рассмотрим на плоскости два семейства параллельных прямых, разбивающих плоскость на равные квадраты (Рис. 1). Любой из этих квадратов называется фундаментальным квадратом или квадратом, порождающим решетку. Множество всех точек пересечения этих прямых называется точечной решеткой или просто решеткой, а сами точки – узлами решетки.
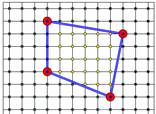
Рис.1.
Чтобы оценить площадь многоугольника на клетчатой бумаге (Рис.1), достаточно подсчитать, сколько клеток покрывает этот многоугольник (площадь клетки мы принимаем за единицу
А также, площадь любого многоугольника, нарисованного на клетчатой бумаге, легко посчитать, представив её как сумму или разность площадей прямоугольных треугольников и прямоугольников, стороны которых идут по линиям сетки, проходящим через вершины нарисованного треугольника. Чтобы вычислить площадь многоугольника, изображенного на рисунке, необходимо достроить его до прямоугольника ABCD, вычислить площадь прямоугольника ABCD, найти площадь заштрихованной фигуры как сумму площадей треугольников и прямоугольников её составляющих, вычесть её из площади прямоугольника. И хотя многоугольник и выглядит достаточно просто, для вычисления его площади нам придется потрудиться. А если бы многоугольник выглядел более причудливо, как на следующих рисунках?
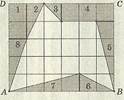
Рис.2
Оказывается, площади многоугольников, вершины которых расположены в узлах решетки, можно вычислять гораздо проще: есть формула, связывающая их площадь с количеством узлов, лежащих внутри и на границе многоугольника. Эта замечательная и простая формула называется формулой Пика: S = В +  - 1, где S – площадь многоугольника, В – число узлов решетки, расположенных строго внутри многоугольника, Г – число узлов решетки, расположенных на его границе, включая вершины. Будем рассматривать только такие многоугольники, все вершины которых лежат в узлах решетки.
- 1, где S – площадь многоугольника, В – число узлов решетки, расположенных строго внутри многоугольника, Г – число узлов решетки, расположенных на его границе, включая вершины. Будем рассматривать только такие многоугольники, все вершины которых лежат в узлах решетки.
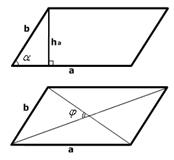
Площадь параллелограмма
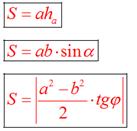
Теорема: Площадь параллелограмма равна произведению его основания на высоту.
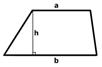
Площадь трапеции
Теорема: Площадь трапеции равна произведению полусуммы ее оснований на высоту.

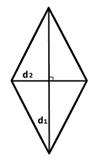
Площадь ромба
Площадь ромба равна половине произведения длин его диагоналей.
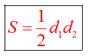
Площадь прямоугольника
Теорема: Площадь прямоугольника равна произведению длин его сторон.

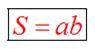
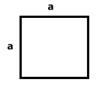
Площадь квадрата
Площадь квадрата равна квадрату длины его стороны.
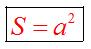
Площадь круга и его частей
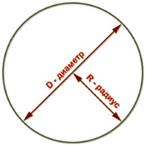
Круг – конечная часть плоскости, ограниченная окружностью.
Круговой сектор-часть круга, ограниченная двумя радиусами и дугой окружности.
Круговой сегмент – часть круга, ограниченная хордой и дугой окружностью.
Площадь круга
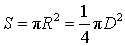
Площадь кругового сегмента
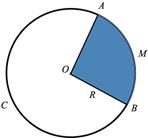
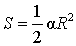
Площадь кругового сегмента
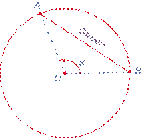
S сегмента=Sсектора-Sтреугольника
S сегмента=Sсектора+Sтреугольника
Решая задачи на уроках в классе и изучив литературу и Интернет-источники по теме, можно выделить несколько методов нахождения площади многоугольника, построенного на клетчатой бумаге так, что все его вершины находятся в узлах пересечения клеток. Проблема заключается в том, чтобы в каждом случае выбрать наиболее подходящий, т.е. менее трудоемкий и более быстрый способ. Так появилась идея сравнить найденные способы по ряду критериев и создать сравнительную таблицу.
Практическая часть
Метод разбиения на части
Фигура разбивается с помощью вертикальных и горизонтальных отрезков так, чтобы многоугольник полностью (без отверстий и наложений) заполняли получившиеся при разбиении прямоугольники и прямоугольные треугольники. Сумма всех площадей фигур, полученных в результате такого разбиения равна площади данного многоугольника.
 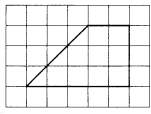 Рис. Рис.
| 1) Разобьем фигуру на прямоугольник и прямоугольный треугольник.
2) Найдем площадь прямоугольника, это можно сделать просто подсчетом клеточек S=6кв.ед.
3) Найдем площадь треугольника S=0,5*3*3=4,5кв.ед.
4) Найдем сумму площадей этих фигур 6+4,5=10,5кв.ед.
|
Способ подходит для любых многоугольников, но он достаточно трудоемкий, и при работе нужно быть внимательным и не допускать вычислительных ошибок.
Формула Пика
Оказывается, площади многоугольников, вершины которых расположены в узлах сетки, можно вычислять гораздо проще: есть формула, связывающая их площадь с количеством узлов, лежащих внутри и на границе многоугольника. Эта замечательная и простая формула называется формулой Пика3. Так как про этот метод ничего не написано в учебнике, нужно рассмотреть его поподробнее.
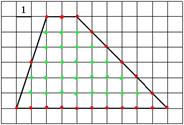 Рис.
Рис.
| Формула Пика:
Г=20 (точки на границе),
В=27 (точки внутри)
S=В+Г/2-1=27+10-1=36
|
Вот такие методы решения задач на нахождение площадей многоугольников на сетке удалось найти. Они все несложные, но при решении конкретной задачи важно выбрать наиболее подходящий.
Заключение
Нахождение площади многоугольника может стать очень интересным и познавательным занятием, совсем не сложным и трудоемким, как кажется на первый взгляд.
Поработав с материалом и подготовив его к применению на практике, я сделала следующие выводы:
1. Существуют различные методы нахождения площади многоугольника.
2. Обычный лист бумаги в клетку может выполнять роль инструмента для вычисления площади многоугольника, если этот многоугольник на нем изображен.
3. Формула Пика - самый универсальный метод решения задач данного типа. С помощью формулы Пика можно найти площадь любого многоугольника, построенного на клетчатой бумаге с вершинами в узлах клеток.
4. Проведенная работа и полученные в результате ее выполнения сравнительная таблица4 и тренажер по отработке способа решения задач по формуле Пика дадут школьникам возможность решения задач на нахождение площадей на сетке наиболее простым способом. Эти знания можно применить на уроках математики, для выполнения олимпиадных заданий. А еще эти материалы могут пригодиться выпускникам девятых и одиннадцатых классов при подготовке к экзаменам.
Список использованной литературы:
1. Горина Л.В. Одна за всех… Формула Пика. Материал для самообразования учащихся.// Основа, №3 (27), с. 24-28. Режим доступа: http://gorinalw.3dn.ru/OSNOVA/osnova-3-2013.pdf
2. Рисс Е. А. Математический клуб «Кенгуру» Выпуск № 8 (изд. второе). – Санкт-Петербург, 2009.
3. Екимова М. А.,Кукин Г. П. Задачи на разрезание. М.: МЦНМО, 2002. Режим доступа: http://www.math.ru/lib/files/pdf/kukin.pdf
4. Линдгрен Г. Занимательные задачи на разрезание./Пер. с англ. Ю.Н. Сударева. Под ред. и с послесл. И.М. Яглома. М.: Мир.-1977. – 256 с.
5. Спивак А.В. Тысяча и одна задача по математике: Кн. Дя учащихся 5-7 кл. – М.: Просвещение, 2002. – 207 с.
6. Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б. и др. Геометрия. 7-9 классы: учеб. для общеобразоват. Организаций. – 3-е изд. – М.: Просвещение, 2014. -383 с.
7. Трошин В. В. Занимательные дидактические материалы по математике. Сборник заданий. Выпуск 2. – М.: Глобус, 2008.
8. Болотин И. Б., Добрышина Л. Ф. Смоленские математические олимпиады школьников (готовимся к ЕГЭ). Смол.гос. ун-т; Смоленск: СмолГУ, 2008.
9. Геометрия на клетчатой бумаге. Малый МЕХмат МГУ. Режим доступа: http://mmmf.msu.ru/archive/20082009/KanunnikovKuznetsov/2.html
10. Григорьева Г. И. Подготовка школьников к олимпиадам по математике: 5 – 6 классы. Метод.пособие. – М.: Глобус, 2009.
11. Дынкин Е. Б., Молчанов С. А., Розенталь А. Л. Математические соревнования. Арифметика и алгебра. – М.: Наука, 1970.
12. Жарковская Н. М., Рисс Е. А. Геометрия клетчатой бумаги. Формула Пика // Математика, 2009, № 17, с. 24-25.
Введение
«Решение задач – практическое искусство, подобное
плаванию, катанию на лыжах или игре на фортепиано;
научиться ему можно, только подражая хорошим
образцам и постоянно практикуясь»
Д. Пойя
Увлечение математикой часто начинается с размышления над какой-то особенно понравившейся задачей. Я рассмотрел множество разных заданий, и такие как задачи на клетчатой бумаге.
Оказывается, задачи, связанные с бумагой в клеточку, достаточно разнообразны. Можно вычислять площади многоугольников, нарисованных на клетчатом листке, а раскраска клеточек помогает решать многие задачи.
Актуальность данного проекта заключается в том, что для упрощения решения и экономичности времени можно использовать формулу Пика, а решение таких задач, формирует вычислительные навыки, способствует развитию логического мышления и повышает интерес к изучению математики.
Цель работы:
- выяснить существует ли чёткая классификация и структурирование задач на клетчатой бумаге по методам и способам решения.
Задачи:
- рассмотреть задачи на нахождение площади многоугольника, задачи на разрезание,
на нахождение расстояния и игры на клетчатой бумаге;
-провести анализ работы и сформулировать вывод.
Объект исследования: задачи на клетчатой бумаге.
Предмет исследования: многообразие задач на клетчатой бумаге.
Методы исследования: сравнение, обобщение, аналогии, изучение литературных и Интернет-ресурсов, анализ и классификация информации.
Гипотеза: возможно непонимание учащимися задач на клетчатой бумаге объясняется отсутствием алгоритмов решения этих задач и необходимостью проявить творческий подход и смекалку. Предположим, что исследуя задачи на клетчатой бумаге, расширятся знания о геометрических фигурах и повысится интерес к изучению математики.
Теоретическая часть
Формула Пика
Георг Пик – австрийский математики. Он известен своей теоремой о вычислении площади многоугольника, которая появилась в его восьмистраничной работе 1899 года. Эта теорема оставалась незамеченной в течение некоторого времени после того, как Пик её опубликовал, однако в 1949 г. польский математик Гуго Штейнгауз включил теорему (или как её ещё называют — формулу) в свой знаменитый «Математический калейдоскоп». С этого времени теорема Пика стала широко известна. В Германии формула Пика включена в школьные учебники.
При решении задач на клетчатой бумаге необходимы понятия решетки и узла.
Клетчатая бумага (точнее — ее узлы), на которой мы часто предпочитаем рисовать и чертить, является одним из важнейших примеров точечной решетки на плоскости.
Рассмотрим на плоскости два семейства параллельных прямых, разбивающих плоскость на равные квадраты (Рис. 1). Любой из этих квадратов называется фундаментальным квадратом или квадратом, порождающим решетку. Множество всех точек пересечения этих прямых называется точечной решеткой или просто решеткой, а сами точки – узлами решетки.

Рис.1.
Чтобы оценить площадь многоугольника на клетчатой бумаге (Рис.1), достаточно подсчитать, сколько клеток покрывает этот многоугольник (площадь клетки мы принимаем за единицу
А также, площадь любого многоугольника, нарисованного на клетчатой бумаге, легко посчитать, представив её как сумму или разность площадей прямоугольных треугольников и прямоугольников, стороны которых идут по линиям сетки, проходящим через вершины нарисованного треугольника. Чтобы вычислить площадь многоугольника, изображенного на рисунке, необходимо достроить его до прямоугольника ABCD, вычислить площадь прямоугольника ABCD, найти площадь заштрихованной фигуры как сумму площадей треугольников и прямоугольников её составляющих, вычесть её из площади прямоугольника. И хотя многоугольник и выглядит достаточно просто, для вычисления его площади нам придется потрудиться. А если бы многоугольник выглядел более причудливо, как на следующих рисунках?

Рис.2
Оказывается, площади многоугольников, вершины которых расположены в узлах решетки, можно вычислять гораздо проще: есть формула, связывающая их площадь с количеством узлов, лежащих внутри и на границе многоугольника. Эта замечательная и простая формула называется формулой Пика: S = В +  - 1, где S – площадь многоугольника, В – число узлов решетки, расположенных строго внутри многоугольника, Г – число узлов решетки, расположенных на его границе, включая вершины. Будем рассматривать только такие многоугольники, все вершины которых лежат в узлах решетки.
- 1, где S – площадь многоугольника, В – число узлов решетки, расположенных строго внутри многоугольника, Г – число узлов решетки, расположенных на его границе, включая вершины. Будем рассматривать только такие многоугольники, все вершины которых лежат в узлах решетки.
Доказательство формулы Пика.
Пусть В – число узлов решетки, расположенных строго внутри многоугольника, Г – число узлов решетки, расположенных на его границе, включая вершины, 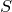 — его площадь. Тогда справедлива формула Пика:
— его площадь. Тогда справедлива формула Пика: 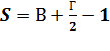 . [1]
. [1]
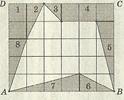
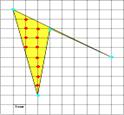
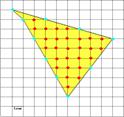
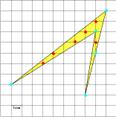
Пример 1. Вычислить площадь многоугольника, изображенного на клетчатой бумаге по формуле Пика.
S = В + Г/ 2 – 1
В = 14, Г = 8, S = 14 + 8/2 -1= 17 (кв.ед.)





 - 1, где S – площадь многоугольника, В – число узлов решетки, расположенных строго внутри многоугольника, Г – число узлов решетки, расположенных на его границе, включая вершины. Будем рассматривать только такие многоугольники, все вершины которых лежат в узлах решетки.
- 1, где S – площадь многоугольника, В – число узлов решетки, расположенных строго внутри многоугольника, Г – число узлов решетки, расположенных на его границе, включая вершины. Будем рассматривать только такие многоугольники, все вершины которых лежат в узлах решетки.




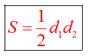

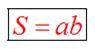

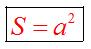

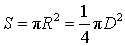

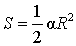


 Рис.
Рис.
 Рис.
Рис.
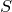 — его площадь. Тогда справедлива формула Пика:
— его площадь. Тогда справедлива формула Пика: 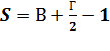 . [1]
. [1]



