

Организация стока поверхностных вод: Наибольшее количество влаги на земном шаре испаряется с поверхности морей и океанов (88‰)...

Семя – орган полового размножения и расселения растений: наружи у семян имеется плотный покров – кожура...

Организация стока поверхностных вод: Наибольшее количество влаги на земном шаре испаряется с поверхности морей и океанов (88‰)...

Семя – орган полового размножения и расселения растений: наружи у семян имеется плотный покров – кожура...
Топ:
Оценка эффективности инструментов коммуникационной политики: Внешние коммуникации - обмен информацией между организацией и её внешней средой...
Генеалогическое древо Султанов Османской империи: Османские правители, вначале, будучи еще бейлербеями Анатолии, женились на дочерях византийских императоров...
Интересное:
Лечение прогрессирующих форм рака: Одним из наиболее важных достижений экспериментальной химиотерапии опухолей, начатой в 60-х и реализованной в 70-х годах, является...
Национальное богатство страны и его составляющие: для оценки элементов национального богатства используются...
Аура как энергетическое поле: многослойную ауру человека можно представить себе подобным...
Дисциплины:
|
из
5.00
|
Заказать работу |
|
|
|
|
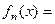
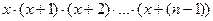 .
.
Также эта функция ещё обозначается 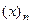 и носит название «символ Похгаммера», при
и носит название «символ Похгаммера», при 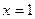 её значение совпадает с факториалом n!.
её значение совпадает с факториалом n!.
Запишем многочлены такого типа, начиная с младших степеней, как в формуле Тейлора.

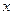 , коэффициент
, коэффициент 

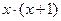 =
= 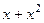 , коэффициенты
, коэффициенты 
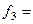
 =
= 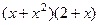 =
=  ,
,
коэффициенты 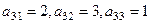 ,
,
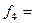
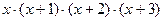 =
= 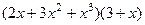 =
= 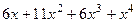 , коэффициенты
, коэффициенты  .
.
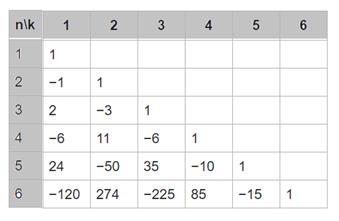
Обратим внимание на то, что последовательность коэффициентов точно такая же, как строка из чисел Стрилинга при том же  .
.
Докажем, что этой действительно так, и закономерность будет верна при любом  .
.
Вспомним, что мы доказали формулу для чисел Стирлинга 1 рода:  .
.
Докажем, что точно такая же закономерность будет и для коэффициентов этих многочленов.
Пусть 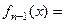
 =
=
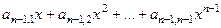 , впрочем, очевидно, старший коэффициент
, впрочем, очевидно, старший коэффициент 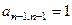 , исходя из строения множителей этого многочлена. Рассмотрим подробнее, как именно образуется коэффициент при степени
, исходя из строения множителей этого многочлена. Рассмотрим подробнее, как именно образуется коэффициент при степени 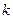 у многочлена следующей степени.
у многочлена следующей степени.
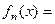

либо 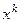 на константу, либо
на константу, либо 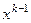 на
на 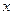 .
.
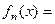
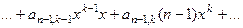 =
=
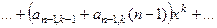
Итак,  .
.
Это точно соответствует  .
.
Для малых n мы непосредственно видели, что последовательность коэффициентов совпадает со строкой чисел Стирлинга 1 рода (база индукции). В каждой следующей строке последовательность коэффициентов вычисляется по такому же закону, как и числа Стирлинга 1 рода.
Если рассматривать многочлен
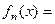
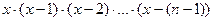 , то получим коэффициенты такие же по модулю, но со знакочередованием.
, то получим коэффициенты такие же по модулю, но со знакочередованием.

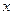 , коэффициент
, коэффициент 

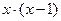 =
= 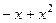 , коэффициенты
, коэффициенты 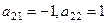
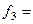
 =
= 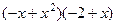 =
= 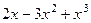 ,
,
коэффициенты  ,
,
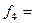
 =
= 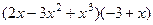 =
=
 .
.
обратим внимание, что при формировании, например, 2-й степени умножаются 2 отрицательных и 2 положительных коэффициента, при формировании 3-й оба раза отрицательный на положительный, то есть, коэффициенты получаются те же самые, что и в рассмотренном выше случае, но только с чередующимися знаками. Именно они и называются «числами Стирлинга 1 рода со знаком», обозначение 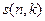 .
.
|
|
Верны такие формулы:
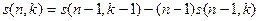 .
.
Числа Стирлинга со знаком:
Матрица перестановки (подстановки). Орбита элемента, неподвижная точка перестановки.
Вернёмся к рассмотрению  - «симметрической группы» перестановок степени
- «симметрической группы» перестановок степени  . Смысл такого подробного изучения перестановок (подстановок) проявится ещё и на 2 курсе при изучении теории групп. Так, будет изучена теорема Кэли о том, что всякая конечная группа
. Смысл такого подробного изучения перестановок (подстановок) проявится ещё и на 2 курсе при изучении теории групп. Так, будет изучена теорема Кэли о том, что всякая конечная группа 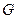 из
из  элементов изоморфна некоторой подгруппе группы перестановок своих элементов
элементов изоморфна некоторой подгруппе группы перестановок своих элементов 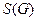 .
.
Матрица подстановки.
Всякую подстановку из  элементов можно представить в виде матрицы порядка
элементов можно представить в виде матрицы порядка  , состоящей из
, состоящей из  единиц и
единиц и  нулей, причём множество таких матриц образует группу по умножению, изоморфную данной группе подстановок.
нулей, причём множество таких матриц образует группу по умножению, изоморфную данной группе подстановок.
Строение матрицы таково: если 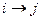 в подстановке, то
в подстановке, то  .
.
При этом множество таких матриц, имеющих определитель 1 (таковых ровно половина от  ) соответствует подгруппе чётных подстановок.
) соответствует подгруппе чётных подстановок.
Например, 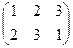 соответствует
соответствует  ,
,
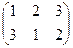 соответствует
соответствует 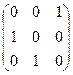 , их произведение есть тождественная подстановка, умножим в то же время и матрицы, получим матрицу
, их произведение есть тождественная подстановка, умножим в то же время и матрицы, получим матрицу  :
:


 =
= 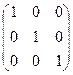 .
.
Кстати, подстановка, квадрат которой равен тождественной,  , называется инволюцией.
, называется инволюцией.
Метод построения отображения из множества подстановок во множество матриц такой структуры ясен, докажем окончательно для произвольного случая, что это изоморфизм.
1) Если  в подстановке
в подстановке  ,
,  , в остальных местах строки
, в остальных местах строки  и столбца
и столбца 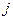 нули.
нули.
2) Если 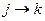 в подстановке
в подстановке  ,
, 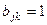 , в остальных местах строки
, в остальных местах строки 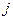 и столбца
и столбца 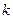 нули.
нули.
При умножении матриц, строка  матрицы
матрицы  умножается на столбец
умножается на столбец 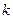 матрицы
матрицы 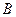 , в результате 1 на
, в результате 1 на 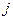 -м месте в обоих случаях, получаем
-м месте в обоих случаях, получаем 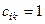 . Все прочие
. Все прочие 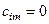 в этой строке, так как при умножении на другие столбцы, там 1 не на
в этой строке, так как при умножении на другие столбцы, там 1 не на  -м месте, а на другом.
-м месте, а на другом.
Нейтральные элементы в этих изоморфных группах соответственно - тождественная подстановка и матрица  .
.
Взаимосвязь наличия циклов и строения матрицы.
|
|
 соответствует матрице
соответствует матрице 
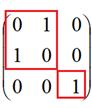
Блочно-диагональная матрица, подматрица 2 порядка (1,2 стр и 1,2 столбец) содержит обе единицы, и в остальных местах в 1,2 стр и 1,2 столбце только нули.
Если для перестановки  верно
верно 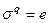 , то
, то 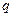 называется порядком перестановки
называется порядком перестановки  .
.
Квадрат подстановки:
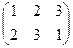
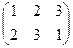 =
=
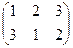

| Умножим 3-й раз (выч. куб)
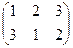
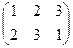 =
=

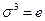 тождественная
Порядок 3. тождественная
Порядок 3.
|
Функция Ландау: Для всякого  ,
,  = наибольший порядок элемента в группе подстановок
= наибольший порядок элемента в группе подстановок  .
.
(для n, найти такую подстановку, чтобы умножение её на себя как можно дольше не приводило к тождественной).
 равна наибольшему из НОК по всем разбиениям
равна наибольшему из НОК по всем разбиениям  на суммы натуральных чисел. Например, если подстановки из 5 элементов, то возможны такие разбиения: 5=1+4, 5=2+3.
на суммы натуральных чисел. Например, если подстановки из 5 элементов, то возможны такие разбиения: 5=1+4, 5=2+3.
НОК(1,4)=4, НОК(2,3)=6. Максимальный порядок подстановки 5 порядка есть число 6. Можно разбить на 2 цикла, по 2 и 3 элемента, и тождественная подстановка получится только при 6 степени подстановки:
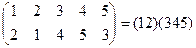 , последующие степени:
, последующие степени:
2-я  , 3-я
, 3-я  , 4-я
, 4-я 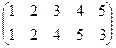 ,
,
5-я 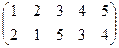 , 6-я
, 6-я  .
.
 , так как 7=3+4, НОК = 12.
, так как 7=3+4, НОК = 12.
При разбиении на циклы из 3 и 4 элементов, повтор возникает только через 12 раз.
 - подстановка 12 порядка.
- подстановка 12 порядка.
Если  , то
, то  называется неподвижной точкой перестановки (цикл длины 1).
называется неподвижной точкой перестановки (цикл длины 1).
Пусть дана перестановка  . Если
. Если 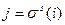 для некоторого
для некоторого 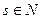 , то говорят, что
, то говорят, что 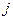 принадлежит
принадлежит  -орбите элемента
-орбите элемента  .
.
Если  ни при каком
ни при каком  , то эти числа находятся в разных классах. Орбиты - непересекающиеся множества, сумма мощностей равна
, то эти числа находятся в разных классах. Орбиты - непересекающиеся множества, сумма мощностей равна  . Количество разбиений на независимые циклы задаётся числами Стирлинга 1 рода, а количество разбиений на подмножества (орбиты) числами Стирлинга 2 рода.
. Количество разбиений на независимые циклы задаётся числами Стирлинга 1 рода, а количество разбиений на подмножества (орбиты) числами Стирлинга 2 рода.
ЛЕКЦИЯ 8. 6.3.2021.
ГЛАВА 2. Числовые системы.
|
|
|

Папиллярные узоры пальцев рук - маркер спортивных способностей: дерматоглифические признаки формируются на 3-5 месяце беременности, не изменяются в течение жизни...

Таксономические единицы (категории) растений: Каждая система классификации состоит из определённых соподчиненных друг другу...

Индивидуальные и групповые автопоилки: для животных. Схемы и конструкции...

Архитектура электронного правительства: Единая архитектура – это методологический подход при создании системы управления государства, который строится...
© cyberpedia.su 2017-2024 - Не является автором материалов. Исключительное право сохранено за автором текста.
Если вы не хотите, чтобы данный материал был у нас на сайте, перейдите по ссылке: Нарушение авторских прав. Мы поможем в написании вашей работы!