Элемент 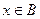 называется минимальным в подмножестве
называется минимальным в подмножестве 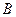 , если не существует меньшего элемента, т.е.
, если не существует меньшего элемента, т.е. 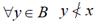 .
.
Элемент 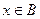 называется наименьшим в подмножестве
называется наименьшим в подмножестве 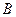 , если он меньше каждого в этом подмножестве, т.е.
, если он меньше каждого в этом подмножестве, т.е. 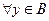
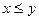 .
.
Наименьший является минимальным, но не наоборот.
(Для сравнения: для функций, локальных минимумов несколько, наименьшее значение одно).
Пример. Во множестве всех подмножеств из 3 элементов (состоящем из 8 элементов), где цветным выделено подмножество В, элементы (1) и (23) являются минимальными. Если отбросить (23), то в оставшемся подмножестве (1) будет наименьшим.

Отличие между наименьшим и минимальным элементами покажем с помощью графа и матрицы отношения.
Рассмотрим упорядоченное множество 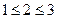 .
.
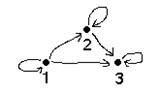
Тот факт, что 1 наименьший, проявляется в том, что от него стрелки направлены ко всем.
Тот факт, что минимальный (нет меньшего, чем он), означает, что к нему не направлена стрелка ни от какого элемента, кроме него самого.
Теперь рассмотрим матрицу отношения.
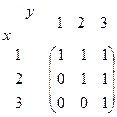
В матрице, тот факт, что «1» наименьший элемент, выражается в том, что во всей строке 1, а не 0 (он меньше, чем любой). Тот факт, что он минимальный (меньше него не существует, кроме него самого), означает, что в столбце все 0, кроме пересечения с диагональю.
Изоморфизмы упорядоченных множеств.
Два частично упорядоченных множества называются изоморфными, если между ними существует изоморфизм, т.е. взаимно однозначное отображение  , сохраняющее порядок:
, сохраняющее порядок:
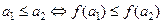 .
.
Примеры
1. Равномощные, но не изоморфные множества. Отрезок  и действительная ось R. Одно множество имеет наибольший элемент, второе нет. (Мощность континуум у обоих).
и действительная ось R. Одно множество имеет наибольший элемент, второе нет. (Мощность континуум у обоих).
2. Изоморфные. Интервал  и действительная ось R.
и действительная ось R.
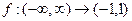 ,
,  .
.
Функция биективная и монотонная, 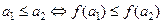 .
.
3. Z и Q с отношением порядка <. Если допустить, что они изоморфны, то соседние целые числа  <
<  переходят в
переходят в 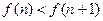 . Тогда рациональным числам между
. Тогда рациональным числам между 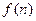 и
и 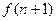 должны соответствовать целые числа между
должны соответствовать целые числа между  и
и  , но они не существуют. Равномощны, но не изоморфны.
, но они не существуют. Равномощны, но не изоморфны.
Не равномощные не являются изоморфными множествами (нет никакой биективной функции).
Лемма. Следующие 2 свойства эквивалентны:
1. Существует непустое подмножество, не содержащее минимальный элемент,
2. Существует бесконечная строго убывающая последовательность

Из (1) следует (2): Если подмножество не имеет минимального элемента, можно построить последовательность: возьмём 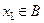 . Он не минимальный, то есть существует
. Он не минимальный, то есть существует 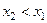 . Элемент
. Элемент 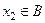 также не минимальный, поэтому существует
также не минимальный, поэтому существует  и т.д.
и т.д.
Из (2) следует (1): если  , то подмножество, состоящее из всех
, то подмножество, состоящее из всех 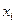 , не имеет минимального элемента.
, не имеет минимального элемента.
Это можно переформулировать следующим образом:
Лемма.
1. любое непустое подмножество имеет минимальный элемент,
2. не существует бесконечной строго убывающей последовательности.
Всё сказанное приводит нас к такому понятию:
Фундированное множество – частично упорядоченное множество, у которого любое непустое подмножество имеет минимальный элемент.
Примеры. N с отношением делимости, 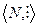 ,
,
а также N с отношением  .
.
В 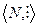 подмножество
подмножество 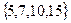 минимальные элементы: 5 и 7.
минимальные элементы: 5 и 7.
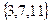 минимальные элементы 3, 7 и 11 (они не делятся ни на какое число из этого подмножества).
минимальные элементы 3, 7 и 11 (они не делятся ни на какое число из этого подмножества).
ЛЕКЦИЯ 4. 20.2.2021.
Теорема. Пусть  два фундированных частично упорядоченных множества. Тогда их декартово произведение
два фундированных частично упорядоченных множества. Тогда их декартово произведение 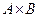 , порядок на котором определён следующим образом:
, порядок на котором определён следующим образом:

является фундированным множеством.
Примечание. Такой порядок называется лексикографическим порядком.
Доказательство. Допустим, что существовала бы бесконечная убывающая последовательность элементов.
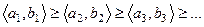
В силу того, что 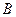 фундированное множество, произойдёт стабилизация по вторым координатам, а так как
фундированное множество, произойдёт стабилизация по вторым координатам, а так как  фундировано, то затем по первым координатам. Напр., рассмотрим
фундировано, то затем по первым координатам. Напр., рассмотрим  .
.
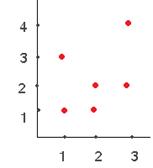
(1,1) (2,1) (2,2) (3,2) (1,3) (3,4) Расположение по порядку.
Возрастание по 2-м координатам, а если вторые одинаковы, то по первым.
 из-за второй координаты, а если сравнивать
из-за второй координаты, а если сравнивать
(2,2) и (3,2), то  .
.
Таким образом,  фундировано. Аналогично доказывается, что не только
фундировано. Аналогично доказывается, что не только  , но и любое
, но и любое 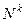 является фундированным.
является фундированным.
Линейно упорядоченное множество – частично упорядоченное множество, в котором любые 2 элемента сравнимы.
При этом минимальный элемент является наименьшим, для таких множеств эти понятия совпадают.
Пример: множество целых чисел Z относительно порядка 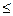 , любые 2 числа сравнимы. При этом множество не фундированное.
, любые 2 числа сравнимы. При этом множество не фундированное.
Каким образом линейная упорядоченность отражается на матрице отношения? Либо 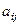 либо
либо 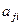 равно 1, оба элемента не могут быть 0. Таким образом, в матрице
равно 1, оба элемента не могут быть 0. Таким образом, в матрице 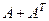 все элементы, кроме диагонали, равны 1. Если отношение нестрогого порядка, то на диагонали будут числа 2, если строгого - то 0.
все элементы, кроме диагонали, равны 1. Если отношение нестрогого порядка, то на диагонали будут числа 2, если строгого - то 0.
Примечание. Если множество мощности континнум то рассматривать не матрицу, а функцию 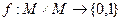 (область определения квадрат
(область определения квадрат  ). Если
). Если 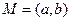 то над треугольником 1, над другим треугольником 0.
то над треугольником 1, над другим треугольником 0.
Вполне упорядоченное множество – линейно упорядоченное множество, у которого любое непустое подмножество имеет минимальный элемент (линейно упорядоченное и фундированное).
Пример: множество натуральных чисел N относительно 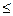 .
.
Для целых чисел это не верно, так как нет минимального элемента для многих подмножеств.
Соберём в таблицу все эти типы множеств:
| Условие на
min элемент:
| Не любые 2 элемента сравнимы
| Любые 2 элемента сравнимы
|
| Нет
| Частично упорядоченное
| Линейно упорядоченное
|
| Есть
| Фундированное
| Вполне упорядоченное
|
Определение. Цепь - подмножество, любые 2 элемента которого сравнимы, т.е. линейно упорядоченное подмножество частично упорядоченного множества.

Красным выделена цепь.
Верхняя грань – это максимальный элемент цепи (он же наибольший, в этом случае).
Лемма Цорна и теорема Цермело - утверждения, эквивалентные аксиоме выбора.
Лемма Цорна. Частично упорядоченное множество, в котором каждая цепь (то есть линейно упорядоченное подмножество) имеет верхнюю грань (то есть максимальный элемент, который одновременно является наибольшим), содержит максимальный элемент.
Пример, когда это нарушается. Во множестве 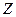 , для отношения делимости. Нет максимального элемента, поэтому должна существовать цепь, не имеющая верхнюю грань. Подмножество
, для отношения делимости. Нет максимального элемента, поэтому должна существовать цепь, не имеющая верхнюю грань. Подмножество 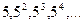 образует цепь, она не имеет верхнюю грань.
образует цепь, она не имеет верхнюю грань.
(Идея док). Если множество не содержит максимальный элемент, то для 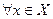
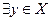 такой, что
такой, что  . Рассмотрим элемент
. Рассмотрим элемент 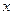 . Но для него должен существовать
. Но для него должен существовать  . Для
. Для 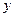 аналогично,
аналогично, 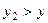 , но он тоже не максимальный, тогда существует
, но он тоже не максимальный, тогда существует 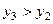 и т.д. В этом случае существует вполне упорядоченное подмножество
и т.д. В этом случае существует вполне упорядоченное подмножество
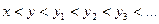 , не имеющее наибольшего элемента.
, не имеющее наибольшего элемента.
Теорема Цермело. Всякое множество можно вполне упорядочить.
N-арные отношения.
Можно рассматривать не только подмножество 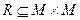 декартового квадрата, но и больших степеней, например,
декартового квадрата, но и больших степеней, например,  . Получим n-арные отношения.
. Получим n-арные отношения.
Пример: На множестве натуральных чисел, 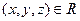
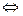
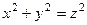 ,
,  . (0,с,с) (6,8,10) также.
. (0,с,с) (6,8,10) также.
Аналогично для n=4: 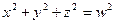 (0,3,4,5).
(0,3,4,5).
Перерыв
Элементы комбинаторики.
Упорядоченная выборка из 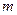 элементов множества мощности
элементов множества мощности  называется размещением, неупорядоченная - сочетанием.
называется размещением, неупорядоченная - сочетанием.
Докажем некоторые базовые формулы.
1) Число размещений m элементов из n, с учётом порядка, без повторений 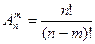 .
.
Один из  элементов ставим на 1 место. Далее один из оставшихся
элементов ставим на 1 место. Далее один из оставшихся  на 2 место, затем остаётся
на 2 место, затем остаётся 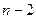 элементов и так далее.
элементов и так далее.
Число 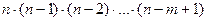 равно
равно 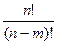 .
.
Пример. Есть 10 цифр, сколько последовательностей из 4 цифр можно составить, если использованную цифру уже нельзя учитывать?
Ответ 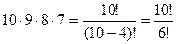 .
.
1а) Число размещений с повторениями. (Если из множества можно снова выбрать уже выбранный элемент, допустим, не он сам, а только информация о нём ставится на определённое место).
Первый раз выбираем один из  , второй раз снова один из
, второй раз снова один из  и так
и так 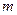 раз. Формула
раз. Формула  .
.
Пример. В алфавите есть 33 буквы. Сколько разных «слов», т.е. упорядоченных наборов из 4 букв можно составить? 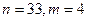 . Ответ
. Ответ  .
.
2) Число сочетаний из n по m, без учёта порядка, без повторений 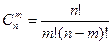 .
.
Аналогично прошлому случаю, но порядок, в котором расположены эти 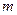 элементов, не важен. Тогда получится в
элементов, не важен. Тогда получится в  раз меньше случаев, так как
раз меньше случаев, так как  это количество перестановок порядка
это количество перестановок порядка 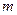 .
.
Есть и другое обозначение: 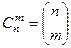 .
.
Пример. Сколько способов выбрать 2 карандаша из 4.
 .
.
Конкретно: 1,2 1,3 1,4 2,3 2,4 3,4.
2а) Число сочетаний из n по m, без учёта порядка, с повторениями

Пример. Сколько есть способов купить 5 ручек двух различных фирм? 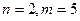 .
. 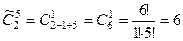 .
.
ААААА | АААА | Б ААА | ББ АА | БББ А | ББББ | БББББ
В этом случае, в отличие от числа сочетаний без повторений, может быть m > n. Выведем формулу  .
.
Есть n типов, разделительных линий между типами подмножеств:  .
.
Получается число сочетаний  . Разделительные линии могут оказаться и рядом, если из какого-то подмножества ничего не выбрано, этот случай тоже учтён.
. Разделительные линии могут оказаться и рядом, если из какого-то подмножества ничего не выбрано, этот случай тоже учтён.
Пример. Сколько есть способов купить 5 ручек трёх различных фирм?  .
. 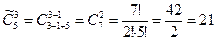 .
.
Разделительные линии на местах (p,q),вот все способы:
| (1,2) | | ВВВВВ
|
|
|
|
|
|
| (1,3) | Б | ВВВВ
| (2,3) А | | ВВВВ
|
|
|
|
|
| (1,4) | ББ | ВВВ
| (2,4) А | Б | ВВВ
| (3,4) АА| | ВВВ
|
|
|
|
| (1,5) | БББ | ВВ
| (2,5) А | ББ | ВВ
| (3,5) АА | Б | ВВ
| (4,5) ААА | | ВВ
|
|
|
| (1,6) | ББББ | В
| (2,6) А | БББ | В
| (3,6) АА | ББ | В
| (4,6) ААА | Б | В
| (5,6) АААА | | В
|
|
| (1,7) | БББББ |
| (2,7) А | ББББ |
| (3,7) АА | БББ |
| (4,7) ААА | ББ |
| (5,7) АААА | Б |
| (6,7) ААААА | |
|
3) Число перестановок 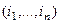 без повторений равно
без повторений равно  (доказывали по индукции в 1 семестре).
(доказывали по индукции в 1 семестре).
3а) Число перестановок 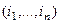 с повторениями.
с повторениями.
Пусть есть 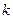 различных элементов
различных элементов 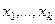 . Перестановкой с повторениями состава
. Перестановкой с повторениями состава 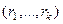 называется упорядоченный набор длины
называется упорядоченный набор длины  , где элемент
, где элемент 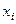 встречается
встречается 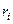 раз.
раз.
 .
.
Идея доказательства: всего  перестановок, при этом если там есть
перестановок, при этом если там есть 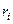 одинаковых элементов, то количество делится на
одинаковых элементов, то количество делится на  .
.
Примеры. Сколько способов переставить буквы в слове «книга»?
Все буквы разные, значит, перестановка без повторений,  .
.
Сколько способов переставить буквы в слове «мороз»?
Здесь есть 2 одинаковые буквы, перестановка состава (2,1,1,1).
Фактически, в любой перестановке, надо отождествить две «о».
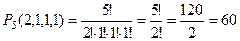 .
.
Если две о вместе, то было бы 4! = 24.
ЛЕКЦИЯ 5. 25.2.2021.
Соберём в таблицу все 6 полученных формул:
|
| Без повторений
| С повторениями
|
| Перестановки
| 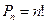
| 
|
| Размещения
| 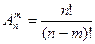
| 
|
| Сочетания
| 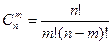
| 
|
Свойства  .
.
Свойство симметрии.
Доказать свойство:  (поставить
(поставить 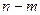 элементов, чтобы
элементов, чтобы 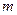 мест остались пустыми, можно тем же самым количеством способов).
мест остались пустыми, можно тем же самым количеством способов).
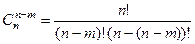 =
=  =
=  .
.
При этом крайние случаи: 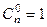 ,
,  .
.
Свойство Паскаля.
Доказать формулу  .
.
 =
= 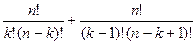
вынесем общие множители, насколько это возможно:
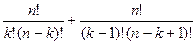 =
= 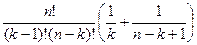
приведём к общему знаменателю в скобке.
 =
=  =
=
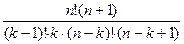 =
= 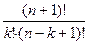 =
=  =
= 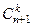 .
.
Биномиальные коэффициенты.
Число сочетаний  оказывается связано с коэффициентами бинома Ньютона
оказывается связано с коэффициентами бинома Ньютона 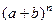 .
.
Вспомним хорошо известные формулы квадрата и куба суммы.


далее
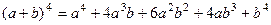
...
Их можно представить в виде
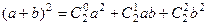
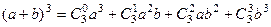 .
.
В общем виде
 .
.
Докажем, что коэффициенты бинома Ньютона и дальше подчиняются этой закономерности. (Методом индукции).
База индукции - было уже ранее (верно для 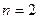 ,
,  ).
).
Пусть  верно для n, докажем для
верно для n, докажем для  .
.
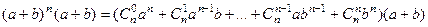 =
=

 =
=
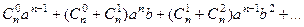
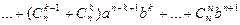 .
.
Ранее доказано, что  .
.
Тогда все слагаемые, кроме крайних, можно записать так:  .
.
При этом для крайних коэффициентов  ,
,  .
.
Тогда получаем:
 .
.
индукционный шаг выполнен, формула верна и для  .
.
Биномиальные коэффициенты можно вычислять с помощью «треугольника Паскаля». Каждое число равно сумме двух вышестоящих, которые слева и справа от него.
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
- чтобы вычислить  не нужно раскрывать все скобки, достаточно взять коэффициенты из строки треугольника Паскаля.
не нужно раскрывать все скобки, достаточно взять коэффициенты из строки треугольника Паскаля.
Производящая функция последовательности биномиальных коэффициентов:  .
.
Функция 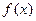 называется производящей функцией последовательности
называется производящей функцией последовательности  , если её разложение в степенной ряд имеет вид
, если её разложение в степенной ряд имеет вид 
 =
= 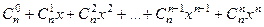 .
. 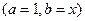 .
.
Свойство суммы.
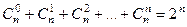 .
.
Множество всех подмножеств из 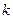 элементов, сумма по всем
элементов, сумма по всем 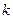 , получается мощность множества всех подмножеств.
, получается мощность множества всех подмножеств.
(Сумма всех чисел строки треугольника Паскаля равна степени 2)
Другое доказательство - из бинома Ньютона при 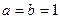 .
.

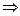
 .
.
Свойство разности.
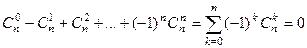 .
.
Докажем это. Положим 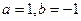 в формуле бинома Ньютона.
в формуле бинома Ньютона.
 .
.
Таким образом,  =
=  .
.
Свойство максимума (следует из свойства симметрии).
Если n чётно, то существует один максимальный коэффициент при 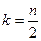 , если нечётно, то два одинаковых максимальных при
, если нечётно, то два одинаковых максимальных при  и
и 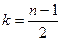 .
.
Задача о беспорядках
Число беспорядков, вывод формулы субфакториала (!n).
Выведем формулу количества подстановок, не оставляющих ни одного элемента на своём месте. Это число называется числом беспорядков, или субфакториалом!n.
Для этого сначала выведем формулу, сколько существует подстановок, оставляющих на месте хотя бы один элемент.
Множество перестановок, оставляющих 1 на месте, состоит из  перестановок. Аналогично, чтобы оставить 2 на месте, надо переставить
перестановок. Аналогично, чтобы оставить 2 на месте, надо переставить  остальных чисел, т.е.
остальных чисел, т.е.  перестановок. И так до номера n. Это мощности рассмотренных множеств
перестановок. И так до номера n. Это мощности рассмотренных множеств  . Но сумма мощностей не равна
. Но сумма мощностей не равна  из-за того, что эти множества частично пересекаются. Так, если 1 остаётся на месте и 2 тоже, то перестановка принадлежит
из-за того, что эти множества частично пересекаются. Так, если 1 остаётся на месте и 2 тоже, то перестановка принадлежит 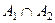 и мы учли её 2 раза. Вспомним ранее доказанную формулу включений и исключений.
и мы учли её 2 раза. Вспомним ранее доказанную формулу включений и исключений.
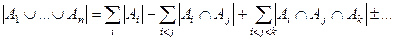
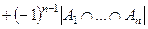 .
.
Сколько перестановок оставляют на месте 2 элемента? Расположение двух элементов задаётся числом 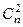 , а остальные можно переставить
, а остальные можно переставить 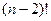 способов. Надо из
способов. Надо из 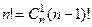 вычесть
вычесть 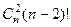 . Но при этом мы лишнее количество раз вычли то количество перестановок, которое сохраняет 3 элемента, и.т.д. По формуле включений и исключений, количество перестановок, сохраняющих на месте хоть какие-то числа, равно:
. Но при этом мы лишнее количество раз вычли то количество перестановок, которое сохраняет 3 элемента, и.т.д. По формуле включений и исключений, количество перестановок, сохраняющих на месте хоть какие-то числа, равно:
 .
.
(напомним что 0!=1). На самом деле, окончание формулы проще:
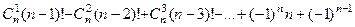 .
.
Посчитаем, представляя число сочетаний по формуле 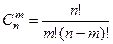 .
.
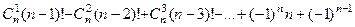 =
=
 =
=
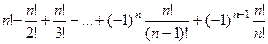 .
.
Чтобы найти число перестановок, не сохраняющих ни одного числа, надо эту величину вычесть из  .
.  =
=
(знаки все меняются на противоположные).
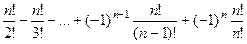 .
.
Итак, 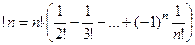 .
.
Для 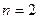 :
: 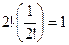 . Одна перестановка из двух тождественная, а вторая не сохраняет на месте ни одно из чисел 1 и 2.
. Одна перестановка из двух тождественная, а вторая не сохраняет на месте ни одно из чисел 1 и 2.
Например, для  :
:
 =
=  =
= 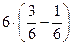 = 2.
= 2.
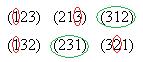
Красным показано, где число k остаётся на месте k, зелёным оставшиеся перестановки, их две.
Например, для 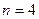 :
:
 =
= 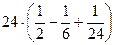 =
= 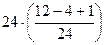 = 9.
= 9.

Для 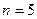 :
:
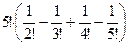 =
=  =
= 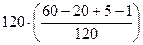 =
=
 (перечислять все 120 не будем).
(перечислять все 120 не будем).
Вывод рекуррентной формулы.
Можно находить!n и с помощью рекурсивной (рекуррентной) формулы. Оказывается, что субфакториал равен произведению 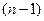 и суммы двух предыдущих его значений.
и суммы двух предыдущих его значений.
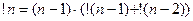 .
.
Например, 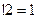 ,
, 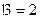 ,
,  ,
, 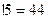 .
.
 .
.
 .
.
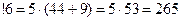 .
.
Докажем эту рекуррентную формулу для общего случая.
Подробнее раскроем выражение 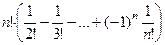 для номеров
для номеров 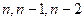 .
.
Для номера n: 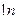 =
=
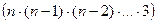
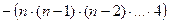 +...
+... 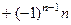
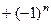 .
.
Для двух предыдущих:  и
и  :
:

 +...
+... 


 +...
+... 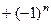
Если их сложить, то на всех местах одни и те же слагаемые идут с коэффициентами 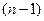 и 1, то есть суммарно
и 1, то есть суммарно  .
.
Таким образом, в сумме получается ровно то же самое, что есть для 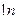 , только без коэффициента
, только без коэффициента 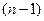 .
.
Причём в конце,  умножится на
умножится на 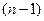 и станет именно то, что было в последних 2 слагаемых для
и станет именно то, что было в последних 2 слагаемых для 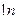 , то есть
, то есть 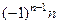
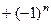 .
.
Например, рассмотрим чтобы было более понятно, при конкретных  .
.
n=6 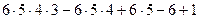
n=5 
n=4 
Суммирование двух (n=5 и n=4) последних порождает
 .
.
Если умножить на 5, получим
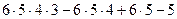 (в конце для n то же самое, только
(в конце для n то же самое, только 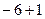 ).
).
Итак, доказали, что 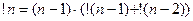 .
.
Итак, вывели 2 формулы для вычисления субфакториала, то есть количества перестановок, не сохраняющих на месте ни одного элемента:
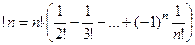
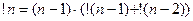
Задача о числе разбиений
Числа Стирлинга — комбинаторные понятия, введенные Джеймсом Стирлингом в середине XVIII века.
Числа Стирлинга первого рода — количество перестановок порядка n с k циклами, обозначается 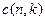 .
.
Числа Стирлинга второго рода — количество неупорядоченных разбиений n-элементного множества на k непустых подмножеств.
Обозначается 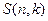 .
.
Число Белла — число всех неупорядоченных разбиений n-элементного множества, обозначаемое 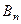 . Число Белла можно вычислить как сумму чисел Стирлинга второго рода
. Число Белла можно вычислить как сумму чисел Стирлинга второго рода 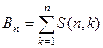 .
.
Сначала изучим числа Стирлинга 2 рода и числа Белла.
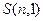 очевидно, равно 1 (одно непустое подмножество именно из n элементов и состоит).
очевидно, равно 1 (одно непустое подмножество именно из n элементов и состоит).
Также нетрудно вывести формулы для  .
.
1-элементное и 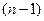 - элементное - таких есть
- элементное - таких есть 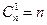 .
.
2-элементное и 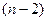 - элементное - таких есть
- элементное - таких есть 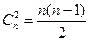 .
.
И так далее. 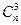 ,
,  , …
, …
При этом 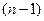 и 1-элементное затем будут учтены повторно, в количестве
и 1-элементное затем будут учтены повторно, в количестве 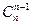 =
= 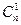 штук, Аналогично
штук, Аналогично 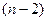 и 2 и т.д.
и 2 и т.д.
Если n печётно то надо делить пополам. Если n чётно то тоже: допустим, во множестве из 4 элементов рассматриваем два 2-элементных подмножества. Их 6, по числу сочетаний 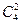 . «Оставшиеся» 2 элемента из 4 образуют «второе» подмножество, но они же в другой раз образуют «первое».
. «Оставшиеся» 2 элемента из 4 образуют «второе» подмножество, но они же в другой раз образуют «первое».
(1,2)(3,4) (1,3)(2,4) (1,4)(2,3) (2,3)(1,4) (2,4)(1,3) (3,4)(1,2)
Полусумма всех чисел из строки треугольника Паскаля, без единиц. 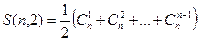 .
.
При этом, если учесть, что  (мощность множества всех подмножеств), а крайние числа равны 1, то
(мощность множества всех подмножеств), а крайние числа равны 1, то
 =
= 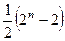 =
= 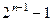 .
.
Другое доказательство.
С другой стороны, можно рассуждать и так: при разбиении на 2 подмножества, рассмотрим множество всех собственных подмножеств (не равных пустому и М), его мощность  . Так как дополнение, где характеристическая функция 0, позже будет учтено, а исходное подмножество наоборот, станет дополнением, то получается, что каждое разбиение мы учли 2 раза, и надо поделить на 2. Получается
. Так как дополнение, где характеристическая функция 0, позже будет учтено, а исходное подмножество наоборот, станет дополнением, то получается, что каждое разбиение мы учли 2 раза, и надо поделить на 2. Получается 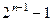 .
.
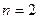
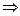
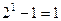 ,
,

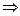
 ,
,
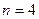
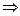
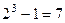 ,...
,...
и далее мы видим во 2 столбце квадрат двойки минус 1.
2,4,8,16,32,64,128,... 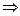 1,3,7,15,31,63,127,...
1,3,7,15,31,63,127,...
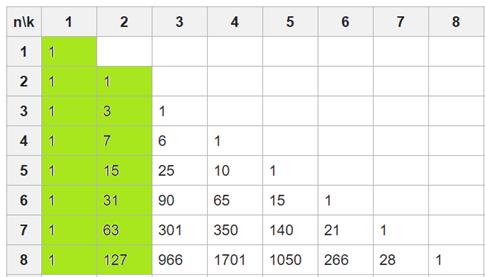
Таким образом, строение 1 и 2 столбцов ясно.
Теперь про 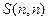 и
и  .
.
 , так как при наличии n элементов, разбиение на n подмножество всего одно: каждый элемент есть отдельное подмножество.
, так как при наличии n элементов, разбиение на n подмножество всего одно: каждый элемент есть отдельное подмножество.
Докажем, что 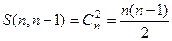 .
.
Если разбиение на 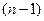 подмножеств, то одно из множеств двухэлементное, тогда остальные могут быть только 1-элементными.
подмножеств, то одно из множеств двухэлементное, тогда остальные могут быть только 1-элементными.
Количество 2-элементных подмножеств вычисляется так:
 .
.
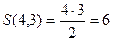 ,
,  ,
, 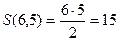 ,...
,...
Итак, мы понимаем, как считать следующую часть таблицы:

ЛЕКЦИЯ 6. 27.2.2021.
Теперь выведем общие формулы для произвольных  , которые позволят вычислять все остальные элементы.
, которые позволят вычислять все остальные элементы.
Верна следующая рекуррентная (рекурсивная) формула:
Доказательство.
1) Пусть предыдущее множество (без последнего элемента) разбито на 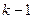 подмножеств. В этом случае,
подмножеств. В этом случае,  -й элемент образует
-й элемент образует 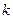 -е подмножество. Количество таких случаев равно
-е подмножество. Количество таких случаев равно  .
.
2) Пусть предыдущее 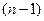 -элементное множество разбито на
-элементное множество разбито на 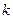 подмножеств. Тогда
подмножеств. Тогда  -й элемент должен быть присоединён к какому-то из уже существующих подмножеств. При любом таком разбиении,
-й элемент должен быть присоединён к какому-то из уже существующих подмножеств. При любом таком разбиении, 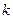 способов сделать это (присоединить к одному из
способов сделать это (присоединить к одному из 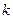 подмножеств). А число случаев, когда
подмножеств). А число случаев, когда 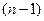 -элементное множество разбито на
-элементное множество разбито на 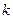 подмножеств, равно
подмножеств, равно 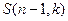 . Итак, добавится
. Итак, добавится 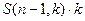 случаев.
случаев.
3) Если 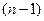 -элементное множество разбито на
-элементное множество разбито на  и менее подмножеств, то
и менее подмножеств, то  -элементное не может быть разбито на
-элементное не может быть разбито на 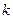 подмножеств, ведь один добавленный
подмножеств, ведь один добавленный  -й элемент не увеличит на 2 подмножества сразу.
-й элемент не увеличит на 2 подмножества сразу.
4) Если 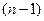 -элементное множество разбито на
-элементное множество разбито на 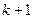 и более подмножеств, то
и более подмножеств, то  -элементное тоже не может быть разбито на
-элементное тоже не может быть разбито на 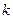 подмножеств, ведь даже включив добавленный
подмножеств, ведь даже включив добавленный  -й эле
-й эле



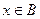 называется минимальным в подмножестве
называется минимальным в подмножестве 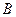 , если не существует меньшего элемента, т.е.
, если не существует меньшего элемента, т.е. 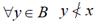 .
.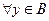
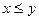 .
.
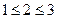 .
. 
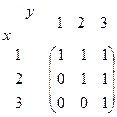
 , сохраняющее порядок:
, сохраняющее порядок: 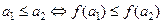 .
.  и действительная ось R. Одно множество имеет наибольший элемент, второе нет. (Мощность континуум у обоих).
и действительная ось R. Одно множество имеет наибольший элемент, второе нет. (Мощность континуум у обоих). и действительная ось R.
и действительная ось R.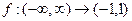 ,
,  .
. <
<  переходят в
переходят в 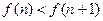 . Тогда рациональным числам между
. Тогда рациональным числам между 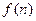 и
и 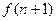 должны соответствовать целые числа между
должны соответствовать целые числа между 
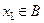 . Он не минимальный, то есть существует
. Он не минимальный, то есть существует 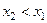 . Элемент
. Элемент 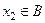 также не минимальный, поэтому существует
также не минимальный, поэтому существует  и т.д.
и т.д.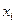 , не имеет минимального элемента.
, не имеет минимального элемента.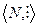 ,
, .
. 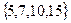 минимальные элементы: 5 и 7.
минимальные элементы: 5 и 7.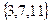 минимальные элементы 3, 7 и 11 (они не делятся ни на какое число из этого подмножества).
минимальные элементы 3, 7 и 11 (они не делятся ни на какое число из этого подмножества). два фундированных частично упорядоченных множества. Тогда их декартово произведение
два фундированных частично упорядоченных множества. Тогда их декартово произведение 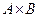 , порядок на котором определён следующим образом:
, порядок на котором определён следующим образом:
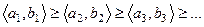
 фундировано, то затем по первым координатам. Напр., рассмотрим
фундировано, то затем по первым координатам. Напр., рассмотрим  .
.
 из-за второй координаты, а если сравнивать
из-за второй координаты, а если сравнивать .
.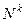 является фундированным.
является фундированным.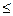 , любые 2 числа сравнимы. При этом множество не фундированное.
, любые 2 числа сравнимы. При этом множество не фундированное.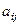 либо
либо 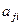 равно 1, оба элемента не могут быть 0. Таким образом, в матрице
равно 1, оба элемента не могут быть 0. Таким образом, в матрице 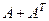 все элементы, кроме диагонали, равны 1. Если отношение нестрогого порядка, то на диагонали будут числа 2, если строгого - то 0.
все элементы, кроме диагонали, равны 1. Если отношение нестрогого порядка, то на диагонали будут числа 2, если строгого - то 0.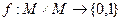 (область определения квадрат
(область определения квадрат  ). Если
). Если 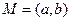 то над треугольником 1, над другим треугольником 0.
то над треугольником 1, над другим треугольником 0.
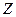 , для отношения делимости. Нет максимального элемента, поэтому должна существовать цепь, не имеющая верхнюю грань. Подмножество
, для отношения делимости. Нет максимального элемента, поэтому должна существовать цепь, не имеющая верхнюю грань. Подмножество 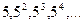 образует цепь, она не имеет верхнюю грань.
образует цепь, она не имеет верхнюю грань.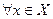
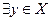 такой, что
такой, что  . Рассмотрим элемент
. Рассмотрим элемент 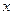 . Но для него должен существовать
. Но для него должен существовать 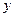 аналогично,
аналогично, 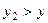 , но он тоже не максимальный, тогда существует
, но он тоже не максимальный, тогда существует 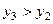 и т.д. В этом случае существует вполне упорядоченное подмножество
и т.д. В этом случае существует вполне упорядоченное подмножество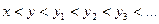 , не имеющее наибольшего элемента.
, не имеющее наибольшего элемента.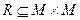 декартового квадрата, но и больших степеней, например,
декартового квадрата, но и больших степеней, например,  . Получим n-арные отношения.
. Получим n-арные отношения.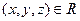
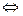
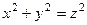 ,
,  . (0,с,с) (6,8,10) также.
. (0,с,с) (6,8,10) также.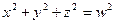 (0,3,4,5).
(0,3,4,5).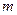 элементов множества мощности
элементов множества мощности 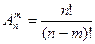 .
.  на 2 место, затем остаётся
на 2 место, затем остаётся 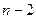 элементов и так далее.
элементов и так далее.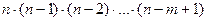 равно
равно 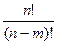 .
. 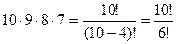 .
.  .
. 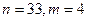 . Ответ
. Ответ  .
. 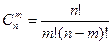 .
. раз меньше случаев, так как
раз меньше случаев, так как 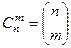 .
.  .
.
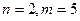 .
. 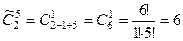 .
.  . Разделительные линии могут оказаться и рядом, если из какого-то подмножества ничего не выбрано, этот случай тоже учтён.
. Разделительные линии могут оказаться и рядом, если из какого-то подмножества ничего не выбрано, этот случай тоже учтён. .
. 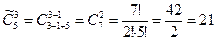 .
. 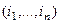 без повторений равно
без повторений равно  (доказывали по индукции в 1 семестре).
(доказывали по индукции в 1 семестре).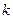 различных элементов
различных элементов 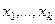 . Перестановкой с повторениями состава
. Перестановкой с повторениями состава 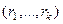 называется упорядоченный набор длины
называется упорядоченный набор длины  , где элемент
, где элемент 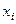 встречается
встречается 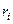 раз.
раз. .
.  .
.  .
.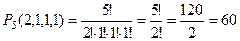 .
. 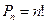
 .
. (поставить
(поставить 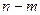 элементов, чтобы
элементов, чтобы 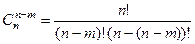 =
=  =
=  .
. 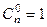 ,
,  .
. .
. =
= 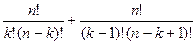
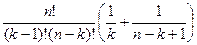
 =
=  =
=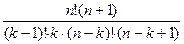 =
= 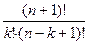 =
=  =
= 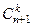 .
. 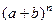 .
. 

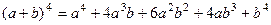
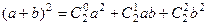
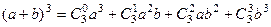 .
.  .
.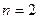 ,
,  ).
).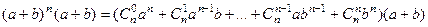 =
=
 =
=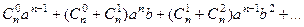
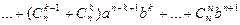 .
. .
. ,
,  .
. .
. не нужно раскрывать все скобки, достаточно взять коэффициенты из строки треугольника Паскаля.
не нужно раскрывать все скобки, достаточно взять коэффициенты из строки треугольника Паскаля. .
.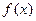 называется производящей функцией последовательности
называется производящей функцией последовательности  , если её разложение в степенной ряд имеет вид
, если её разложение в степенной ряд имеет вид 
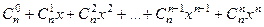 .
. 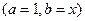 .
.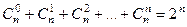 .
.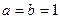 .
.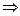
 .
.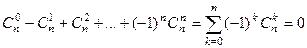 .
.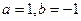 в формуле бинома Ньютона.
в формуле бинома Ньютона. .
.  =
=  .
. 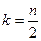 , если нечётно, то два одинаковых максимальных при
, если нечётно, то два одинаковых максимальных при  и
и 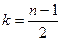 .
. перестановок. Аналогично, чтобы оставить 2 на месте, надо переставить
перестановок. Аналогично, чтобы оставить 2 на месте, надо переставить  . Но сумма мощностей не равна
. Но сумма мощностей не равна 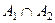 и мы учли её 2 раза. Вспомним ранее доказанную формулу включений и исключений.
и мы учли её 2 раза. Вспомним ранее доказанную формулу включений и исключений.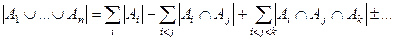
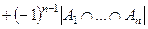 .
.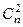 , а остальные можно переставить
, а остальные можно переставить 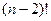 способов. Надо из
способов. Надо из 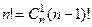 вычесть
вычесть 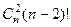 . Но при этом мы лишнее количество раз вычли то количество перестановок, которое сохраняет 3 элемента, и.т.д. По формуле включений и исключений, количество перестановок, сохраняющих на месте хоть какие-то числа, равно:
. Но при этом мы лишнее количество раз вычли то количество перестановок, которое сохраняет 3 элемента, и.т.д. По формуле включений и исключений, количество перестановок, сохраняющих на месте хоть какие-то числа, равно:  .
. 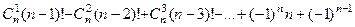 .
. 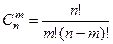 .
. =
=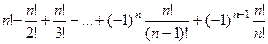 .
.  =
=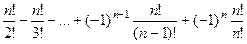 .
.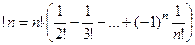 .
. 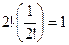 . Одна перестановка из двух тождественная, а вторая не сохраняет на месте ни одно из чисел 1 и 2.
. Одна перестановка из двух тождественная, а вторая не сохраняет на месте ни одно из чисел 1 и 2. =
=  =
= 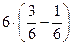 = 2.
= 2.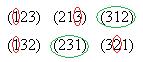
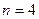 :
: =
= 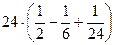 =
= 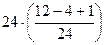 = 9.
= 9.
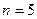 :
: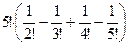 =
=  =
= 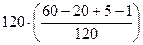 =
= (перечислять все 120 не будем).
(перечислять все 120 не будем). 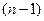 и суммы двух предыдущих его значений.
и суммы двух предыдущих его значений.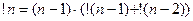 .
.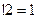 ,
, 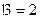 ,
,  ,
, 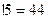 .
. .
.  .
. 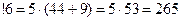 .
.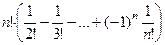 для номеров
для номеров 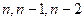 .
.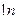 =
=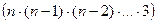
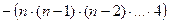 +...
+... 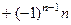
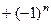 .
. и
и  :
:
 +...
+... 


 +...
+... 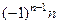
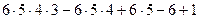


 .
. 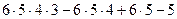 (в конце для n то же самое, только
(в конце для n то же самое, только 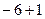 ).
).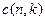 .
.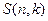 .
.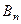 . Число Белла можно вычислить как сумму чисел Стирлинга второго рода
. Число Белла можно вычислить как сумму чисел Стирлинга второго рода 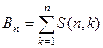 .
.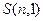 очевидно, равно 1 (одно непустое подмножество именно из n элементов и состоит).
очевидно, равно 1 (одно непустое подмножество именно из n элементов и состоит). .
.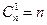 .
.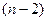 - элементное - таких есть
- элементное - таких есть 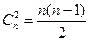 .
.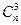 ,
,  , …
, …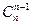 =
= 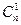 штук, Аналогично
штук, Аналогично 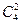 . «Оставшиеся» 2 элемента из 4 образуют «второе» подмножество, но они же в другой раз образуют «первое».
. «Оставшиеся» 2 элемента из 4 образуют «второе» подмножество, но они же в другой раз образуют «первое».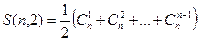 .
. (мощность множества всех подмножеств), а крайние числа равны 1, то
(мощность множества всех подмножеств), а крайние числа равны 1, то =
= 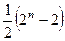 =
= 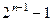 .
. . Так как дополнение, где характеристическая функция 0, позже будет учтено, а исходное подмножество наоборот, станет дополнением, то получается, что каждое разбиение мы учли 2 раза, и надо поделить на 2. Получается
. Так как дополнение, где характеристическая функция 0, позже будет учтено, а исходное подмножество наоборот, станет дополнением, то получается, что каждое разбиение мы учли 2 раза, и надо поделить на 2. Получается 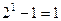 ,
,  ,
, 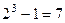 ,...
,... 
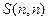 и
и  .
. , так как при наличии n элементов, разбиение на n подмножество всего одно: каждый элемент есть отдельное подмножество.
, так как при наличии n элементов, разбиение на n подмножество всего одно: каждый элемент есть отдельное подмножество.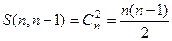 .
.  .
.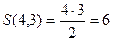 ,
,  ,
, 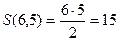 ,...
,...
 , которые позволят вычислять все остальные элементы.
, которые позволят вычислять все остальные элементы.
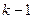 подмножеств. В этом случае,
подмножеств. В этом случае,  .
. 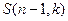 . Итак, добавится
. Итак, добавится 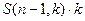 случаев.
случаев. и менее подмножеств, то
и менее подмножеств, то 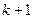 и более подмножеств, то
и более подмножеств, то 

