

Общие условия выбора системы дренажа: Система дренажа выбирается в зависимости от характера защищаемого...

История создания датчика движения: Первый прибор для обнаружения движения был изобретен немецким физиком Генрихом Герцем...

Общие условия выбора системы дренажа: Система дренажа выбирается в зависимости от характера защищаемого...

История создания датчика движения: Первый прибор для обнаружения движения был изобретен немецким физиком Генрихом Герцем...
Топ:
Характеристика АТП и сварочно-жестяницкого участка: Транспорт в настоящее время является одной из важнейших отраслей народного...
Особенности труда и отдыха в условиях низких температур: К работам при низких температурах на открытом воздухе и в не отапливаемых помещениях допускаются лица не моложе 18 лет, прошедшие...
Марксистская теория происхождения государства: По мнению Маркса и Энгельса, в основе развития общества, происходящих в нем изменений лежит...
Интересное:
Распространение рака на другие отдаленные от желудка органы: Характерных симптомов рака желудка не существует. Выраженные симптомы появляются, когда опухоль...
Влияние предпринимательской среды на эффективное функционирование предприятия: Предпринимательская среда – это совокупность внешних и внутренних факторов, оказывающих влияние на функционирование фирмы...
Аура как энергетическое поле: многослойную ауру человека можно представить себе подобным...
Дисциплины:
|
из
5.00
|
Заказать работу |
|
|
|
|
Приходовский М.А.
Алгебра (курс лекций)
ИПМКН ТГУ, группы 932024, 932025
Весна -2021, семестр 2.
ЛЕКЦИЯ 1. 11.2.2021
ГЛАВА 1. Элементы теории множеств и комбинаторики.
Множеством называют совокупность некоторых объектов. Эти объекты называются элементами множества.
Например, множество точек на плоскости, множество чисел, множество матриц.
Обозначения:
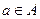 элемент
элемент 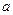 принадлежит множеству
принадлежит множеству  .
.
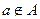 элемент
элемент 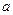 не принадлежит множеству
не принадлежит множеству  .
.
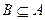 множество
множество  является подмножеством множества
является подмножеством множества  .
.
 множество
множество  является собственным подмножеством множества
является собственным подмножеством множества  (т.е. они не совпадают).
(т.е. они не совпадают).
Объединение 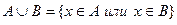
Пересечение 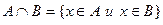
Объединение и пересечение 2 множеств показаны графически:
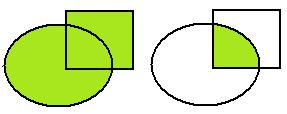
Разность множеств: 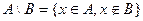 . Показано на чертеже:
. Показано на чертеже:
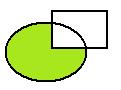
Аналогично,  .
.
Универсальное множество  , дополнение
, дополнение 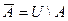 .
.
Очевидно, что  .
.
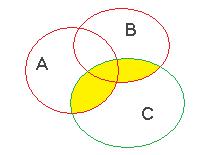
Объединение этих двух разностей называется симметрической разностью, и обозначается так:  =
=  , на чертеже:
, на чертеже:
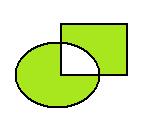
В то же время, это множество можно получить и другим путём: из объединения удалить пересечение. То есть,
 =
= 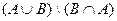 .
.
Другие обозначения: 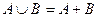 ,
,  .
.
Свойства операций над множествами
Законы идемпотентности: 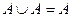 ,
, 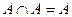 .
.
Операции с пустым множеством 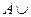 Ø =
Ø = 
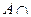 Ø = Ø
Ø = Ø
Коммутативность: 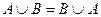 ,
, 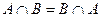
Ассоциативность:


Дистибутивность:
1) 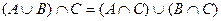
можно записать в виде 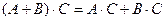 .
.
2) однако, верно также и  .
.
либо в виде  .
.
Замена разности пересечением:  .
.
Док-во. Если 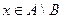 , это означает, что
, это означает, что 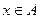 , но при этом
, но при этом 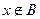 .
.
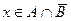 означает то же самое - что одновременно выполнены условия
означает то же самое - что одновременно выполнены условия 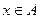 ,
, 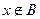 .
.
Лемма. (закон де Моргана). Объединение множеств есть дополнение к пересечению дополнений всех этих множеств.
|
|

Доказательство. Пересечение дополнений - это множество, содержащее элементы, не принадлежащие ни 1-му, ни 2-му,... ни n множеству. Дополнение к построенному - означает, что противоположно ситуации, когда не принадлежит никакому из них, т.е. принадлежит хотя бы одному из них.
1) дополнение к А 2) дополнение к В 3) пересечение дополнений
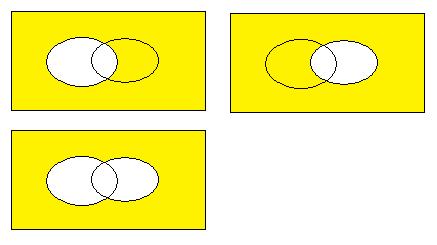
Декартово произведение и декартова степень.
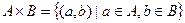
 .
.
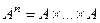 .
.
Булеан. 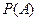 или
или  - множество всех подмножеств множества
- множество всех подмножеств множества  (включая пустое множество и само
(включая пустое множество и само  ).
).
 - множество всех функций из
- множество всех функций из  в
в  .
.
Если строим подмн-во то отображаем функцией во мн-во из 2 элементов {0,1}. (характеристическая функция)
Числовые множества.
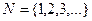 натуральные числа
натуральные числа
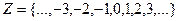 целые числа
целые числа
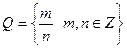 рациональные числа
рациональные числа
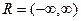 вся действительная ось, действительные числа.
вся действительная ось, действительные числа.
Множество 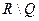 - иррациональные числа.
- иррациональные числа.
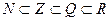 .
.
Функция, аргумент, образ.
Пусть даны 2 множества  ,
,  . Если задан некоторый способ каждому элементу
. Если задан некоторый способ каждому элементу  поставить в соответствие какой-то
поставить в соответствие какой-то 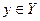 , то говорится, что задана ФУНКЦИЯ из
, то говорится, что задана ФУНКЦИЯ из  в
в  . Обозначение:
. Обозначение: 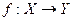 .
. 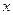 называется аргументом функции, а
называется аргументом функции, а 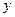 - образом.
- образом.
Мощность конечного множества - количество элементов, из которых оно состоит.
Теорема. Множество всех подмножеств конечного множества имеет мощность 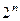 .
.
Например, если n=3, множество 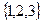 , то подмножества:
, то подмножества:
пустое,  ,
,  ,
,  ,
,  ,
, 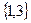 ,
, 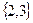 ,
, 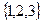 - 8 подмножеств.
- 8 подмножеств.
Доказательство. Составим характеристическую функцию подмножества: факт вхождения элемента в подмножество обозначен через 1, а не вхождения через 0.
Тогда каждое подмножество может быть задано в виде:
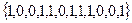
Для одного элемента есть 2 возможности 0 или 1, для двух элементов соответственно  , для трёх
, для трёх  , и.т.д (по индукции).
, и.т.д (по индукции).
Характеристическая функция пересечения равна произведению характеристических функций 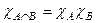 .
.
Характеристическая функция дополнения равна 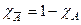 .
.
Лемма.
1) Подмножество счётного множества конечно или счётно.
2) Всякое бесконечное множество содержит счётное подмножество.
|
|
Доказательство.
1) Представим множество  в виде:
в виде:  Выбросим те члены последовательности, которые не принадлежат
Выбросим те члены последовательности, которые не принадлежат  . Оставшиеся элементы образуют либо бесконечную подпоследовательность, либо конечную.
. Оставшиеся элементы образуют либо бесконечную подпоследовательность, либо конечную.
2) Если множество  бесконечно, то можно выбрать последовательность
бесконечно, то можно выбрать последовательность 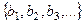 , после выбора каждого
, после выбора каждого 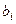 остаётся ещё бесконечное множество неиспользованных элементов, потому что множество бесконечное.
остаётся ещё бесконечное множество неиспользованных элементов, потому что множество бесконечное.
Теорема. Если  бесконечное множество,
бесконечное множество,  конечное или счётное, то
конечное или счётное, то 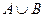 равномощно
равномощно  .
.
Доказательство. Если 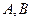 пересекаются, выбросим пересечение из
пересекаются, выбросим пересечение из  , получив новое множество
, получив новое множество  , которое снова будет конечным либо счётным. Далее считаем, что они не пересекаются.
, которое снова будет конечным либо счётным. Далее считаем, что они не пересекаются.
Выделим в  счётное подмножество
счётное подмножество 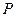 , остаток обозначим
, остаток обозначим 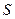 .
.
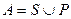 .
.  .
.
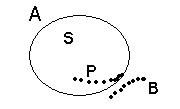
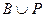 и
и 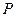 оба счётны, между ними существует взаимно однозначное соответствие. Каждый элемент из
оба счётны, между ними существует взаимно однозначное соответствие. Каждый элемент из 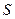 соответствует самому себе. Таким образом, есть взаимно однозначное соответствие между
соответствует самому себе. Таким образом, есть взаимно однозначное соответствие между
 и
и 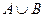 .
.
Теорема. Счётное множество счётных множеств счётно.
Расположим по горизонтали каждое из множеств.
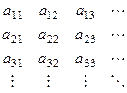
Из элементов этого множества можно образовать такую последовательность: 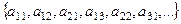
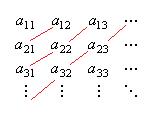
Если исходные множества пересекаются, то часть повторяющихся элементов исключить, получим подпоследовательность, она тоже счётна. При этом она не будет конечна, так как хотя бы одно из исходных множеств счётно.
В обозначениях операций над мощностями, это пишется так:
ﬡ0 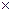 ﬡ0 = ﬡ0
ﬡ0 = ﬡ0
Итак,
1) ﬡ0 + n = ﬡ0
2) ﬡ0 + ﬡ0 = ﬡ0, 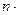 ﬡ0 = ﬡ0
ﬡ0 = ﬡ0
3) ﬡ0 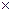 ﬡ0 = ﬡ0
ﬡ0 = ﬡ0
Пусть  - мощность множества А,
- мощность множества А, 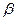 - мощность множества В,
- мощность множества В,
 Ǿ. Тогда
Ǿ. Тогда
Сумма  мощностей - это мощность множества
мощностей - это мощность множества 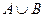 ,
,
Произведение 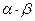 мощностей - это мощность множества
мощностей - это мощность множества  .
.
Для бесконечных мощностей, 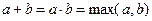 .
.
Примеры.
Множество рациональных чисел  равномощно
равномощно  .
.
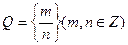 . Декартово произведение
. Декартово произведение 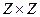 равномощно
равномощно  , можно пронумеровать:
, можно пронумеровать:


В каждом из слоёв конечное количество элементов. Начиная от внутренних прямоугольников, можно пронумеровать все элементы с помощью натуральных чисел.
ЛЕКЦИЯ 2. 13.2.2021
Теорема (Кантора). Множество всех подмножеств счётного множества не является счётным.
Доказательство. Допустим, что искомое множество счётно. Тогда все подмножества можно расположить по порядку, представив то или иное подмножество в каждой строке с помощью 0 и 1 (1 если элемент принадлежит подмножеству, 0 если нет).
|
|
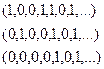
…
Рассмотрим диагональ:

Построим такое подмножество: изменим 0 на 1 и 1 на 0 на всех местах. Напр, здесь было бы 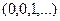 . Оно не совпадает ни с одним из подмножеств, представленных в этой последовательности: с первым не совпадает на 1-м элементе, со вторым на 2-м и так далее.
. Оно не совпадает ни с одним из подмножеств, представленных в этой последовательности: с первым не совпадает на 1-м элементе, со вторым на 2-м и так далее.
Итак, множество всех подмножеств счётного множества не является счётным.
Аналогично, докажем, что (0,1) не является счётным множеством.
Теорема. Интервал (0,1) не является счётным множеством.
Доказательство. Пусть все действительные числа, составляющие (0,1), образуют счётное множество. Каждое из них представим в виде десятичной дроби, 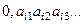 Расположим по порядку эти числа, если множество счётное:
Расположим по порядку эти числа, если множество счётное:
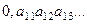
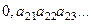
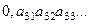
....
Можно рассмотреть такое число:  , взяв значения десятичных разрядов по диагонали.
, взяв значения десятичных разрядов по диагонали.
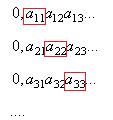
Если теперь в  изменить каждую цифру на какую-либо другую, то получим новое число, которое не совпадает ни с одним из имеющихся в этом множестве. Таким образом, множество не счётное.
изменить каждую цифру на какую-либо другую, то получим новое число, которое не совпадает ни с одним из имеющихся в этом множестве. Таким образом, множество не счётное.
Теорема Кантора-Бернштейна.
Если множество  равномощно подмножеству множества
равномощно подмножеству множества  , а
, а  равномощно подмножеству множества
равномощно подмножеству множества  , то
, то  и
и  равномощны.
равномощны.
Доказательство.
Пусть множество  равномощно некоторому
равномощно некоторому  - подмножеству множества
- подмножеству множества  . Т.е. существует некоторая функция
. Т.е. существует некоторая функция  , которая инъективна, но не сюръективна. При этом
, которая инъективна, но не сюръективна. При этом 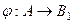 биекция.
биекция.
Аналогично  равномощно некоторому подмножеству
равномощно некоторому подмножеству 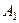 множества
множества  , и существует инъективная функция
, и существует инъективная функция  , при этом
, при этом 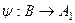 биекция.
биекция.
Тогда для композиции 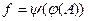 есть некоторое множество
есть некоторое множество 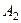 - «образ образа» множества
- «образ образа» множества  . При этом
. При этом 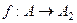 - биекция.
- биекция.
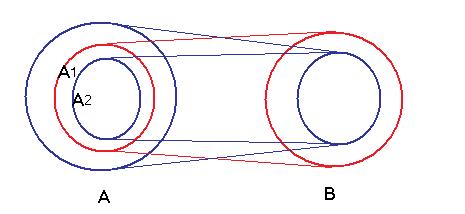
Так как 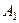 равномощно
равномощно  , то нужно фактически доказать, что равномощны
, то нужно фактически доказать, что равномощны  и
и 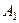 , то есть построить биективное отображение.
, то есть построить биективное отображение.
При этом  равномощны.
равномощны.
Применяя функции  и
и  несколько раз, получим последовательность множеств:
несколько раз, получим последовательность множеств: 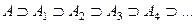 при этом
при этом 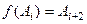 . Пересечение
. Пересечение 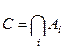 возможно, непустое множество.
возможно, непустое множество.
Обозначим  ,
, 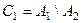 ,... При этом
,... При этом 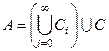 .
.
Биективное отображение 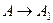 можно построить следующим образом.
можно построить следующим образом.  для нечётных
для нечётных  и для
и для  ,
, 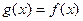 для чётных
для чётных  . При этом
. При этом 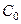 перейдёт в
перейдёт в 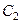 ,
, 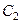 в
в 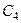 и так далее.
и так далее.
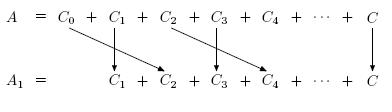
А равномощно А1, А1 равномощно В.
Континуум-гипотеза (проблема континуума) — выдвинутое в 1877 году Георгом Кантором предположение о том, что любое бесконечное подмножество континуума является либо счётным, либо континуальным. Другими словами, гипотеза предполагает, что мощность континуума — наименьшая, превосходящая мощность счётного множества.
|
|
Континуум-гипотеза (первый несчётный кардинал имеет мощность континуума):
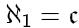
Аксиома выбора
| Для всякого семейства X непустых множеств существует функция f, которая каждому множеству семейства сопоставляет один из элементов этого множества. |
Аксиома выбора была сформулирована и опубликована Эрнстом Цермело в 1904 году. Новая аксиома вызвала бурную полемику и до сих пор не все математики принимают её безоговорочно.
Аксиомы теории множеств.
Система аксиом ZFC (Цермело-Френкеля с аксиомой выбора).
0. Аксиома пустого множества  .
.
1. Условие равенства множеств (аксиома объёмности).
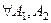 верно, что если
верно, что если 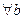 :
:  то
то 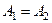 .
.
2. Существование множества из двух элементов (аксиома пары).
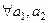
 , такое что
, такое что 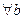 :
: 
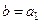 или
или  .
.
3. Аксиома объединения. Из любого семейства 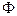 множеств
множеств  можно образовать как минимум одно такое множество
можно образовать как минимум одно такое множество 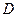 , каждый элемент
, каждый элемент  которого принадлежит хотя бы одному множеству
которого принадлежит хотя бы одному множеству  данного семейства
данного семейства 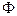 .
.
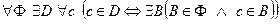 .
.
4. Аксиома пересечения. Из любого семейства 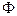 множеств
множеств  можно образовать как минимум одно такое множество
можно образовать как минимум одно такое множество 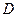 , каждый элемент
, каждый элемент  которого принадлежит всем множествам данного семейства
которого принадлежит всем множествам данного семейства 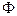 .
.
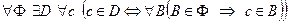 .
.
5. Существование подмножества, элементы которого удовлетворяют некоторому свойству.
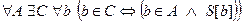 .
.
6. Существование бесконечного множества.
 = {Ø, {Ø}, {Ø,{Ø},... }
= {Ø, {Ø}, {Ø,{Ø},... }
7. Существование образа функции
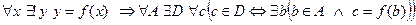
т.е. если кратко, то  .
.
8. Аксиома регулярности. Любое непустое семейство множеств 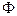 содержит множество
содержит множество  , все элементы которого не принадлежат семейству
, все элементы которого не принадлежат семейству 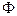 .
.
9. Аксиома выбора. Для любого класса не пересекающихся непустых множеств существует множество, содержащее только по одному элементу из каждого множества.
Прим – бесконечное мн-во прямых на пл-ти (континуум). Не сущ пр, пересекающ со всеми только в 1 точке.
10. Аксиома степени (аксиома булеана). Можно образовать 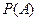 множество всех подмножеств данного множества.
множество всех подмножеств данного множества.
Упорядоченные множества.
Говорят, что на множестве М задано бинарное отношение R, если задано подмножество декартового произведения:  .
.
Примеры. Отношения на множестве 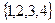
Отношение равенства: 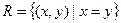
Можно перечислить все пары элементов, находящихся в данном отношении: 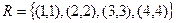 .
.
ЛЕКЦИЯ 3.
18.2.2021
Приходовский М.А.
Алгебра (курс лекций)
ИПМКН ТГУ, группы 932024, 932025
Весна -2021, семестр 2.
ЛЕКЦИЯ 1. 11.2.2021
ГЛАВА 1. Элементы теории множеств и комбинаторики.
Множеством называют совокупность некоторых объектов. Эти объекты называются элементами множества.
|
|
Например, множество точек на плоскости, множество чисел, множество матриц.
Обозначения:
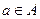 элемент
элемент 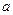 принадлежит множеству
принадлежит множеству  .
.
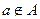 элемент
элемент 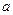 не принадлежит множеству
не принадлежит множеству  .
.
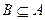 множество
множество  является подмножеством множества
является подмножеством множества  .
.
 множество
множество  является собственным подмножеством множества
является собственным подмножеством множества  (т.е. они не совпадают).
(т.е. они не совпадают).
Объединение 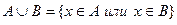
Пересечение 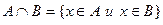
Объединение и пересечение 2 множеств показаны графически:

Разность множеств: 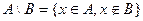 . Показано на чертеже:
. Показано на чертеже:

Аналогично,  .
.
Универсальное множество  , дополнение
, дополнение 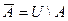 .
.
Очевидно, что  .
.
Объединение этих двух разностей называется симметрической разностью, и обозначается так:  =
=  , на чертеже:
, на чертеже:

В то же время, это множество можно получить и другим путём: из объединения удалить пересечение. То есть,
 =
= 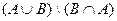 .
.
Другие обозначения: 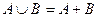 ,
,  .
.
|
|
|

Поперечные профили набережных и береговой полосы: На городских территориях берегоукрепление проектируют с учетом технических и экономических требований, но особое значение придают эстетическим...

Особенности сооружения опор в сложных условиях: Сооружение ВЛ в районах с суровыми климатическими и тяжелыми геологическими условиями...

Организация стока поверхностных вод: Наибольшее количество влаги на земном шаре испаряется с поверхности морей и океанов (88‰)...

Кормораздатчик мобильный электрифицированный: схема и процесс работы устройства...
© cyberpedia.su 2017-2024 - Не является автором материалов. Исключительное право сохранено за автором текста.
Если вы не хотите, чтобы данный материал был у нас на сайте, перейдите по ссылке: Нарушение авторских прав. Мы поможем в написании вашей работы!