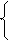ВВЕДЕНИЕ
Курс ’Начертательная геометрия. Инженерная и компьютерная графика’ входит в число дисциплин, составляющих основу инженерного образования.
Предметом начертательной геометрии является изложение и обоснование способов построения плоской модели трехмерного пространства и способов решения задач геометрического характера на базе этой модели. Однако, методы построения и преобразования чертежа преимущественно основаны на словесном описании и запоминании стандартных положений.
Такая трактовка трехмерного пространства не имеет явного сходства с положениями алгебры и тригонометрии, которые предлагают свою математическую модель трехмерного пространства.
Следовательно, начертательная геометрия в классической форме не предполагает использование ЭВМ, т.к. вычислительная техника воспринимает цифровую информацию с последующей математической обработкой ее в графическую. На базе графоматематической модели работают системы автоматизированного (с участием оператора) и автоматического управления объектами.
Одним из условий овладения техническими знаниями является умение читать (выполнять) конструкторские документы с учетом требований ЕСКД (единая система конструкторской документации) и СПДС (система проектной документации для строительства) и использовать при этом ЭВМ в режиме пользователя.
ГЕОМЕТРИЧЕСКОЕ МОДЕЛИРОВАНИЕ
В данной работе рассматривается один из вариантов геометрической модели трехмерного пространства, позволяющей использовать понятия начертательной геометрии на ЭВМ.
Аппарат геометрической модели предполагает измерение длин в метрах и плоских углов в градусах или радианах.

П од длиной подразумевается расстояние между двумя точками. Измерение длины ведется вдоль некоторой прямой от заранее выбранной на ней точки - текущей базы БТ (БТ - точка, координаты которой внутри объекта равны нулю) (рис.1).
Рис. 1. Прямая a. БТ - текущая база; a - обозначенное направление; L - положительное расстояние до точки С; (-В) - отрицательное расстояние до точки D.
3
Линия на чертеже обозначается строчной буквой латинского алфавита.
Если измерение длины ведется в обозначенную сторону прямой, то длина считается положительной и наоборот.
Таким образом, прямая имеет положительное или отрицательное линейное направление.
Кроме того, она имеет угловое направление. Измерение угла принято вести от тригонометрического нуля.
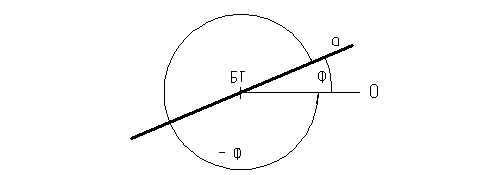
Т ригонометрический ноль – луч 0 с началом в БТ и направлен горизонтально вправо (рис.2).
Измеряется угол до положительного направления прямой. Если измерение угла против часовой стрелки, то угол положительный, по часовой - отрицательный.
 О бозначается угол строчной буквой греческого алфавита.
О бозначается угол строчной буквой греческого алфавита.
Рис.2. Прямая a; j - положительный угол; (-j) - отрицательный угол; БТ – текущая база; 0 – тригонометрический ноль.
Математическая модель той же прямой Y = K ´ X + Y БТ (изменение координаты Y точки прямой с изменением координаты Х; K = tg j).
Прямая линия
Прямая в прямоугольной системе координат задается положением ее текущей базы, например, точкой A(X, Y, Z) и углами наклона к плоскостям проекций a к П1, b к П2, g к П3 (рис. 9).
10
Угол наклона прямой к плоскости измеряется между (7)
самой прямой и ее проекцией на эту плоскость
Под самой прямой на плоской модели будем подразумевать проекцию, длина которой равна модулю.
На основании (4): угол a = (MN)^(M1N1);
угол b = (MN)^(N2M2);
угол g = (MN)^(M3N3).
На рис. 9 прямая задана отрезком АВ. Построены проекции отрезка А1В1- горизонтальная, А2В2 – фронтальная и А3В3 – профильная. Если прямая бесконечна, то она пересекает горизонтальную плоскость П1 в точке М, фронтальную плоскость П2 в точке N и профильную плоскость П3 в точке Р. Точки пересечения прямой с плоскостями проекций называются следами.
Рис. 9
В пространстве точка пересечения прямой АВ, например, с горизонтальной плоскостью проекций П 1 будет точка М – пересечение АВ с ее горизонтальной проекцией А1В1.
На плоской модели прямоугольной системы координат сама прямая АВ отсутствует, есть только ее проекции А1В1, А2В2 и линии связи к оси Х l X.
11
Следовательно, можно построить только горизонтальную проекцию М1, которая совпадет с М, и фронтальную М2.
Уравнение точки М(Х, Y, Z=0). Если точка – пересечение двух прямых, то возможна система уравнений
Z=0 - линия, совпадающая с осью Х
Z=tg j2 ´ X + ZA - фронтальная проекция А2В2
Пересечение этих линий определит фронтальную проекцию М2 (X М, Z=0).
X М – расстояние от начала координат до М2.
Система уравнений для определения координаты Y точки М
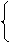 X = X М - линия связи l x к оси Х через М2
X = X М - линия связи l x к оси Х через М2
Y=tg j1 ´ X + YA - горизонтальная проекция А1В1
Пересечение этих линий определит горизонтальную проекцию М1 (X М, Y М).
Y М – расстояние от оси Х до горизонтальной проекции М1.
Фронтальный след прямой АВ – точка N (X, Y =0, Z).
Система уравнений для определения координаты X точки N
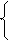
Y=0 - линия, совпадающая с осью Х
Y=tg j1 ´ X + YA - горизонтальная проекция А1В1
Пересечение этих линий определит горизонтальную проекцию N1 (X N, Y =0).
X N – расстояние от начала координат до N1.
Система уравнений для определения координаты Z точки N
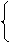 X = X N - линия связи l x к оси Х через N1
X = X N - линия связи l x к оси Х через N1
Z=tg j2 ´ X + ZA - фронтальная проекция А2В2
Пересечение этих линий определит фронтальную проекцию N2 (X N, ZN).
Z N – расстояние от оси Х до фронтальной проекции N2.
Профильный след АВ – точка Р(X =0, Y, Z).
Система уравнений для определения координаты Y точки P
X=0 - линия, совпадающая с осью Y
Y=tg j1 ´ X + YA - горизонтальная проекция А1В1
12
Пересечение этих линий определит горизонтальную проекцию P1 (X=0, YP ).
Y P – расстояние от начала координат до P1.
Система уравнений для определения координаты Z точки P
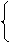 Y = Y P - линия связи l Y к оси Y через P1
Y = Y P - линия связи l Y к оси Y через P1
Z=tg j3 ´ Y + ZA - профильная проекция А3В3
Пересечение этих линий определит профильную проекцию P3 (YP, ZP).
Z P – расстояние от P3 до оси Y.
Длина отрезка и углы наклона к плоскостям проекций
Угол наклона к П1 a прямой АВ (рис. 9) измерен между горизонтальной проекцией А1В1 и самой прямой АВ.
Рис. 10
На рис. 10 прямая задана проекциями А1В1 и А2В2.
Угол наклона к П 1 a можно измерить между фронтальной и горизонтальной проекциями при условии, что А2В2 равна АВ.
А2В2 = АВ ´ Соs (b) (b – угол наклона АВ к П2)
Если угол b = 0, то Соs (b) =0 и А2В2 = АВ.
b = arctg(½YA - YB½ / A2B2)
13
Угол b = 0, если разность координат YA - YB = 0.
Перенесем горизонтальную проекцию во второе текущее положение А21В21 (изменятся координаты X и Y) и повернем вокруг оси ZA (рис. 3) до положения, в котором YA = YB. Координаты Z точек А и В при этом не изменятся, т. к. траектории вращения параллельны П1.
Фронтальные проекции точек А22, В22 будут на пересечениях линий связи к осям X и Z. Фронтальная проекция А22В22 = АВ.
Измерим a = А22В22 Ù А21В21.
Угол наклона к П 2 b можно измерить между горизонтальной и фронтальной проекциями при условии, что А1В1 равна АВ.
А1В1 = АВ ´ Соs (a)
Если угол a = 0, то Соs (a) =0 и А1В1 = АВ.
a = arctg(½ZA - ZB½ / A1B1)
Угол a = 0, если разность координат ZA - ZB = 0.
Перенесем фронтальную проекцию первое текущее положение А12В12 (изменятся координаты X и Z) и повернем вокруг оси YA (рис. 3) до положения, в котором ZA = ZB. Координаты Y точек А и В при этом не изменятся, т. к. траектории вращения параллельны П2.
Горизонтальные проекции точек А11, В11 будут на пересечениях линий связи к осям X и Y. Горизонтальная проекция А11В11 = АВ.
Измерим b = А11В11 Ù А12В12.
Домашняя работа
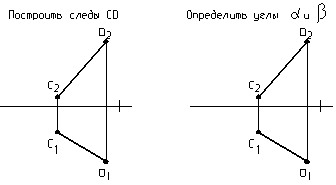
14
Плоскость
В общем виде плоскость задана двумя пересекающимися прямыми (2). Если на этих прямых взять 3 точки, не лежащие на одной прямой, то плоскость будет задана тремя точками. Если 3 упомянутые точки соединить прямыми, то плоскость будет задана треугольником (плоской фигурой в том числе окружностью, проходящей через три точки). Если через точку на первой прямой провести прямую, параллельную второй прямой, то плоскость будет задана двумя параллельными прямыми.
Параметры плоскости:
База, например, точка А(X, Y, Z) в треугольнике АВС (рис. 11).
Угол a - наклон треугольника к плоскости П1.
Угол b - наклон треугольника к плоскости П2.
Угол g - наклон треугольника к плоскости П3.
Перечисленные параметры считаются внешними, их изменение будет менять положение треугольника в пространстве относительно плоскостей проекций.
Натуральная величина треугольника – геометрические размеры (внутренний параметр плоскости).
Рис. 11
Двугранный угол между плоскостями (a Ù П1, b Ù П2, g Ù П3) измеряется линейным углом между линиями пересечения граней этого угла
с третьей плоскостью, которая перпендикулярна данным
15
Плоскость треугольника D(АВС) на рис. 11 задана проекциями горизонтальной А1В1С1 и фронтальной А2В2С2.
Для определения, например, угла a можно изменить угол наклона АВС к плоскости П2 до 90°. Треугольник АВС на плоскость П2 спроецируется в прямую линю А12В12С12 (рис. 11), с которой совпадет линия пересечения D12 треугольника с плоскостью П2. Плоскость П1 перпендикулярна П2 и плоскости пересекаются по оси Х12.
Следовательно, угол a=D12 Ù Х12.
Две плоскости взаимно перпендикулярны, если одна
из них содержит перпендикуляр к другой плоскости.
Чтобы изменить угол A треугольника АВС, в нем надо взять прямую, угол b которой определяется на чертеже. Такой прямой может быть любая прямая, угол a которой = 0.
Возьмем прямую АD(A2D2, A1D1), координаты ZA=XD. A1D1 = AD. Следовательно, угол b AD = A2D2 Ù A1D1.
Повернем горизонтальную проекцию А1В1С1 вокруг оси ZA на угол 90° - b AD и перенесем в положение А11В11С11. Проекция А11D11 ^ Х12, при этом АD будет перпендикулярна П2 и треугольник АВС ^ П2. Фронтальная проекция А12В12С12 совпадет с линией пересечения треугольника с фронтальной плоскостью D12. Угол aАВС будет измерен между D12 Ù Х12.
Натуральную величину треугольника можно найти, если расположить его, например, параллельно плоскости П1. Повернем фронтальную проекцию А12В12С12 треугольника вокруг оси YA1 на угол aАВС и перенесем в положение А22В22С22. Горизонтальные проекции точек А21В21С21 определим на пересечении линий связи к осям Х и Y. Треугольник будет параллелен П1. Горизонтальная проекция треугольника А21В21С21 равна ½АВС½.
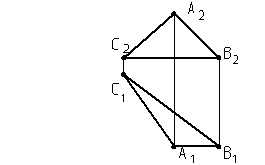
Домашняя работа
Определить углы a и b
треугольника АВС
16
Взаимное положение прямых
Параллельные прямые имеют одинаковые углы наклона к плоскостям проекций, но расстояние между ними не равно 0 (базовая точка одной прямой не принадлежит другой прямой). На рис. 13 прямая a(a 1, a 2)и параллельная ей прямая е(е1, е2) заданы проекциями на плоскости П1 и П2.
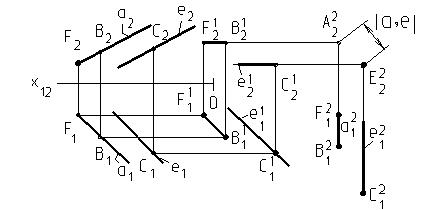
Если прямые параллельны, то параллельны их одноименные проекции (a1 ½½ е1) и (a2 ½½ е2). Для параллельных прямых следует определить расстояние между ними.
Рис. 13
18
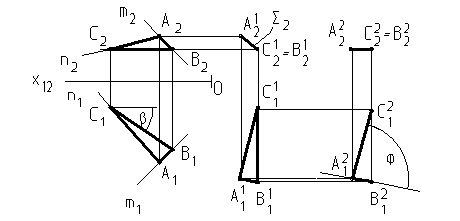
Пересекающиеся прямые имеют общую точку А, проекции которой лежат на одной линии связи к оси Х и совпадают с точками пересечения одноименных проекций, угол между прямыми j больше 0 (рис. 14).
Рис. 14
Скрещивающиеся прямые - не пересекаются (расстояние между ними не равно 0), не параллельны (угол между ними не равен 0). На плоском чертеже точки пересечения одноименных проекций не лежат на одной линии связи к оси Х (рис. 15).
При определении расстояния и угла между прямыми следует исходить из условия, что через две скрещивающиеся прямые можно всегда провести две параллельные плоскости.
Плоскости параллельны, если две пересекающиеся прямые одной
плоскости соответственно параллельны двум пересекающимся
прямым другой плоскости.
Через точку А проведем прямую АЕ, которая параллельна прямой СD.
В результате получим треугольник АВЕ, который параллелен прямой CD.
Прямая параллельна плоскости, если она параллельна прямой,
которая принадлежит плоскости.
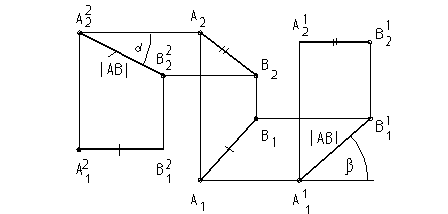
В плоскости АВЕ возьмем прямую АР, угол b AР = 0. Измерим угол aАЕ между А2Р2 и А1Р1, повернем фронтальные проекции С2D2, А2В2Е2 вокруг оси YA на угол 90° - aАЕ и перенесем в положение C12D12, А12В12Е12.
Горизонтальная проекция треугольника А11В11Е11 – прямая, с ней совпадет горизонтальный след плоскости D11. Горизонтальная проекция прямой C11D11 , которая будет параллельна А11В11Е11. С C11D11 совпадет горизонтальный след S11 плоскости, проходящей через CD и параллельной АВЕ.
19
Рис. 15
Расстояние между плоскостями ½D11 S11½ равно расстоянию между прямыми ½CD, AB½.
Угол между прямыми CD Ù AB равен углу между сторонами треугольника АВ Ù АЕ. Измерять угол следует в натуральной величине треугольника.
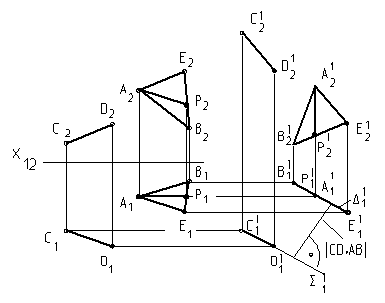
Домашняя работа: Через точку А провести прямую АК, которая пересекает прямые м и n.
20
Литература
1. Тюкин, Н. Н. Инженерная и компьютерная графика: учеб. пособие. Ч. 1 / Н. Н. Тюкин, С. Г. Резико. – Вологда: ВоГТУ, 2009. – 139, [1] с.
2. Тюкин, Н. Н. Инженерная и компьютерная графика: учеб. пособие. Ч. 2 / Н. Н. Тюкин, С. Г. Резико. – Вологда: ВоГТУ, 2009. – 98, [2] с.
МИНОБРНАУКИ РОССИИ
федеральное государственное бюджетное образовательное учреждение
высшего профессионального образования
«Вологодский государственный университет»


Инженерная
и Компьютерная
графика
Вологда
2014 г.
УДК 744: 515
Инженерная и компьютерная графика. Геометрическое моделирование. Методические указания и задания к выполнению аудиторных и домашних работ. – Вологда: ВоГУ, 2014. – 32с.
Методические указания предназначены для освоения методов построения и преобразования чертежа, измерения и изменения длин и углов.
Утверждено редакционно-издательским советом ВоГУ
Составители: Н. Н. Тюкин, доцент кафедры НГиГ
Рецензент В. А. Бабарушкин, канд. техн. наук, доцент
Выписка из протокола № 8
заседания кафедры начертательной геометрии и графики
Вологодского государственного университета
от «» 2014 г.
Слушали: Тюкина Н.Н. о готовности к печати методических указаний «Инженерная и компьютерная графика Геометрическое моделирование. Методические указания и задания к выполнению аудиторных и домашних работ. Методические указания предназначены для студентов электро-энергетического факультета направления подготовки 140400 «Электроснабжение».
Автор: Тюкин Н.Н.
Постановили: методические указания и задания рекомендовать к изданию внутривузовским способом.
И.о.зав. кафедрой НГ и Г Е.В. Соловьева
Секретарь Л.К. Романовская
Выписка
из протокола №____ заседания методического совета
электроэнергетического факультета
Вологодского государственного университета
от «____» _______________2014 г.
Слушали: секретаря методического совета ЭЭФ Корнейчук С. К. об издании внутривузовским способом методических указаний «Инженерная и компьютерная графика. Геометрическое моделирование. Методические указания и задания к выполнению аудиторных и домашних работ. Методические указания предназначены для студентов электро-энергетического факультета направления подготовки 140400 «Электроснабжение».
Автор: Тюкин Н.Н.
Постановили: методические указания и задания рекомендовать к изданию внутривузовским способом.
Председатель
методического совета ЭЭФ Ю.В. Хрусталев
Секретарь
методического совета ЭЭФ С. К. Корнейчук
Рецензия
на методические указания
«Инженерная и компьютерная графика. Геометрическое
моделирование». Методические указания и задания
к выполнению аудиторных и домашних работ.
Разработанные методические указания подготовлены для студентов направления подготовки: 140400 «электроснабжение».
Методические указания по объему и содержанию соответствуют требованиям программы, предъявляемым ФГОС ВПО направлений 140400 по дисциплине «Инженерная и компьютерная графика». Подготовленные методические указания предназначены для самостоятельного выполнения позиционных и метрических задач по разделу электрических схем и чертежей общего вида.
Порядок разделов соответствует последовательности изложения теоретического материала. Содержание и уровень оформления отвечают современным требованиям.
На основании изложенного можно считать, что методические указания будут полезны при изучении курса «Инженерная и компьютерная графика» и могут быть рекомендованы к изданию внутривузовским способом.
Канд. техн. наук, доцент В.А. Бабарушкин
ВВЕДЕНИЕ
Курс ’Начертательная геометрия. Инженерная и компьютерная графика’ входит в число дисциплин, составляющих основу инженерного образования.
Предметом начертательной геометрии является изложение и обоснование способов построения плоской модели трехмерного пространства и способов решения задач геометрического характера на базе этой модели. Однако, методы построения и преобразования чертежа преимущественно основаны на словесном описании и запоминании стандартных положений.
Такая трактовка трехмерного пространства не имеет явного сходства с положениями алгебры и тригонометрии, которые предлагают свою математическую модель трехмерного пространства.
Следовательно, начертательная геометрия в классической форме не предполагает использование ЭВМ, т.к. вычислительная техника воспринимает цифровую информацию с последующей математической обработкой ее в графическую. На базе графоматематической модели работают системы автоматизированного (с участием оператора) и автоматического управления объектами.
Одним из условий овладения техническими знаниями является умение читать (выполнять) конструкторские документы с учетом требований ЕСКД (единая система конструкторской документации) и СПДС (система проектной документации для строительства) и использовать при этом ЭВМ в режиме пользователя.
ГЕОМЕТРИЧЕСКОЕ МОДЕЛИРОВАНИЕ
В данной работе рассматривается один из вариантов геометрической модели трехмерного пространства, позволяющей использовать понятия начертательной геометрии на ЭВМ.
Аппарат геометрической модели предполагает измерение длин в метрах и плоских углов в градусах или радианах.

П од длиной подразумевается расстояние между двумя точками. Измерение длины ведется вдоль некоторой прямой от заранее выбранной на ней точки - текущей базы БТ (БТ - точка, координаты которой внутри объекта равны нулю) (рис.1).
Рис. 1. Прямая a. БТ - текущая база; a - обозначенное направление; L - положительное расстояние до точки С; (-В) - отрицательное расстояние до точки D.
3
Линия на чертеже обозначается строчной буквой латинского алфавита.
Если измерение длины ведется в обозначенную сторону прямой, то длина считается положительной и наоборот.
Таким образом, прямая имеет положительное или отрицательное линейное направление.
Кроме того, она имеет угловое направление. Измерение угла принято вести от тригонометрического нуля.
Т ригонометрический ноль – луч 0 с началом в БТ и направлен горизонтально вправо (рис.2).
Измеряется угол до положительного направления прямой. Если измерение угла против часовой стрелки, то угол положительный, по часовой - отрицательный.
 О бозначается угол строчной буквой греческого алфавита.
О бозначается угол строчной буквой греческого алфавита.
Рис.2. Прямая a; j - положительный угол; (-j) - отрицательный угол; БТ – текущая база; 0 – тригонометрический ноль.
Математическая модель той же прямой Y = K ´ X + Y БТ (изменение координаты Y точки прямой с изменением координаты Х; K = tg j).




 О бозначается угол строчной буквой греческого алфавита.
О бозначается угол строчной буквой греческого алфавита.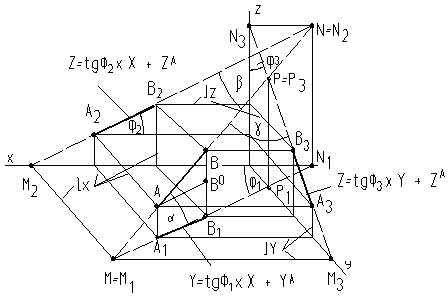
 X = X М - линия связи l x к оси Х через М2
X = X М - линия связи l x к оси Х через М2