Определение. Линейный оператор 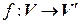 называется невырожденным, если он любой ненулевой вектор переводит в ненулевой.
называется невырожденным, если он любой ненулевой вектор переводит в ненулевой.
Теорема 4.4. Для того чтобы линейный оператор 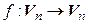 был невырожденным необходимо и достаточно, чтобы его матрица в некотором, а значит, и в любом базисе пространства
был невырожденным необходимо и достаточно, чтобы его матрица в некотором, а значит, и в любом базисе пространства 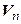 была невырожденной
была невырожденной
►Пусть А – матрица линейного оператора 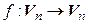 в некотором базисе, Х, как обычно, координатный столбец вектора
в некотором базисе, Х, как обычно, координатный столбец вектора 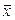 в том же базисе. Тогда
в том же базисе. Тогда
{ f – невырожденный} 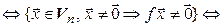
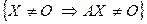
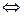
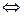 {однородная система линейных уравнений AX = O имеет единственное тривиальное решение}
{однородная система линейных уравнений AX = O имеет единственное тривиальное решение} 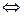 {
{ 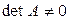 }.
}.
Так как определители подобных матриц совпадают, то утверждение справедливо и для любого базиса. ◄
Теорема 4.5. Для того чтобы линейный оператор 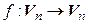 был невырожденным, необходимо и достаточно, чтобы он был взаимно однозначным.
был невырожденным, необходимо и достаточно, чтобы он был взаимно однозначным.
►Пусть 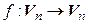 – линейный оператор, А – его матрица в некотором базисе, X и Y – координатные столбцы в том же базисе векторов
– линейный оператор, А – его матрица в некотором базисе, X и Y – координатные столбцы в том же базисе векторов 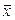 и
и 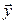 соответственно. Тогда
соответственно. Тогда
{  невырожденный}
невырожденный} 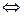
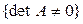
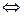 {
{ 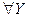 система
система 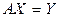 имеет единственное решение}
имеет единственное решение} 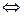 {
{ 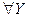
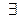 единственный
единственный 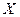 , что
, что 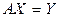 }
} 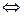
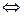 {
{ 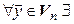 единственный
единственный 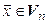 , что
, что 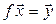 }
} 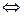 { f – взаимно однозначный}.◄
{ f – взаимно однозначный}.◄
Теорема 4.6. Произведение невырожденных линейных операторов – невырожденный линейный оператор.
►Пусть 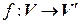 и
и  – невырожденные линейные операторы. Тогда
– невырожденные линейные операторы. Тогда
{ 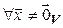 }
} 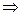 {
{ 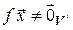 }
} 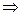 {
{ 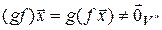 }.
}.
Tаким образом, gf – невырожденный линейный оператор.◄
Обратный линейный оператор
Теорема 4.7. Для любого невырожденного линейногооператора 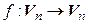 существует единственный обратный оператор
существует единственный обратный оператор 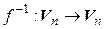 , который также является линейным. При этом, если А – матрица оператора
, который также является линейным. При этом, если А – матрица оператора 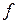 в некотором базисе, то матрица оператора
в некотором базисе, то матрица оператора  в том же базисе совпадает с матрицей
в том же базисе совпадает с матрицей 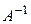 .
.
► Единственность. Пусть некоторый оператор 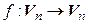 имеет два разных обратных:
имеет два разных обратных: 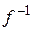 и
и 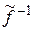 . Тогда
. Тогда

– противоречие.
Существование. Пусть А – матрица оператора 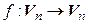 в некотором базисе. Тогда, по теореме 4.4
в некотором базисе. Тогда, по теореме 4.4 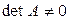 , значит, существует
, значит, существует 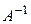 . Обозначим
. Обозначим 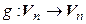 – тот линейный оператор, матрица которого в выбранном базисесовпадаетс
– тот линейный оператор, матрица которого в выбранном базисесовпадаетс 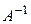 .
.
Так как 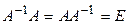 , и так как произведению матриц соответствует произведение операторов, то
, и так как произведению матриц соответствует произведение операторов, то 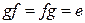 , и, таким образом,
, и, таким образом, 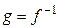 .◄
.◄
Замечание. М ожно доказать, что любой взаимно однозначный линейный оператор 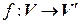 имеет единственный обратный, который тоже является линейным.
имеет единственный обратный, который тоже является линейным.
Изоморфизм линейных пространств
Определение.Изоморфизмом линейных пространств называется взаимно однозначный линейный оператор. Если существует изоморфизм 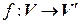 , то линейные пространства
, то линейные пространства 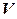 и
и 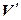 называются изоморфными. Изоморфизм обозначается так:
называются изоморфными. Изоморфизм обозначается так: 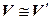 .
.
Так как изоморфизм – взаимно однозначное отображение, то изоморфные объекты содержат одинаковое количество элементов. Кроме того, в силу линейности, действия, производимые над элементами пространства 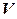 , одновременно производятся и над элементами пространства
, одновременно производятся и над элементами пространства 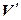 . Поэтому в математике изоморфные объекты не различаются.
. Поэтому в математике изоморфные объекты не различаются.
Свойства изоморфизма
1.  – рефлективность (изоморфизм осуществляет тождественное отображение).
– рефлективность (изоморфизм осуществляет тождественное отображение).
2. 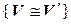
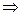
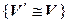 – симметричность (если первый изоморфизм осуществляет с помощью отображения f, то второй – с помощью
– симметричность (если первый изоморфизм осуществляет с помощью отображения f, то второй – с помощью  ).
).
3. { 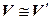 ,
,  }
} 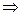
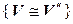 – транзитивность (если первый изоморфизм осуществляется с помощью отображения
– транзитивность (если первый изоморфизм осуществляется с помощью отображения 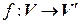 , второй –
, второй –  , то третий изоморфизм осуществляется с помощью отображения
, то третий изоморфизм осуществляется с помощью отображения 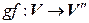 ).
).
Строгого доказательства этих свойств мы не приводим.
Теорема 4.8. Изоморфные линейные пространства имеют одинаковые размерности.
►Пусть 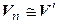 и пусть
и пусть 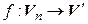 – изоморфизм. Выберем в
– изоморфизм. Выберем в 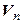 какой-либо базис
какой-либо базис
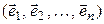 (4.27)
(4.27)
и покажем, что система
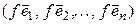 – (4.28)
– (4.28)
базис пространства 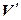 . Действительно, в силу взаимной однозначности f,
. Действительно, в силу взаимной однозначности f, 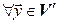
 единственный
единственный  такой, что
такой, что 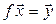 . Тогда, если
. Тогда, если 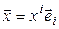 , то
, то  . Значит, (4.28) – система образующих в
. Значит, (4.28) – система образующих в 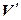 .
.
Докажем теперь линейную независимость (4.28).

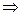 [линейность f ]
[линейность f ] 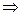
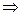
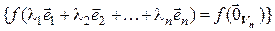
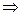 [взаимная однозначность f ]
[взаимная однозначность f ] 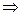
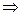
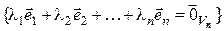
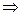 [линейная независимость (4.27)]
[линейная независимость (4.27)] 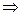
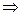
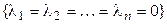
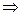 {(4.28) – линейно независима}.
{(4.28) – линейно независима}.
Таким образом, (4.28) – базис в 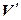 , а значит,
, а значит, 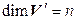 . ◄
. ◄
Теорема 4.9. Все n -мерные линейные пространства над полем Р изоморфны между собой, т. е. существует единственное с точностью до изоморфизма n- мерное линейное пространство над полем Р.
►а) Докажем, что 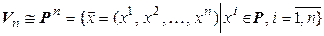 .
.
Выберем в 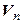 какой-либо базис
какой-либо базис 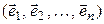 . Тогда
. Тогда 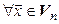 :
: 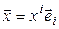 . Обозначим
. Обозначим 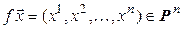 . Очевидно, отображение
. Очевидно, отображение 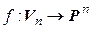 – взаимно однозначное. Кроме того,
– взаимно однозначное. Кроме того, 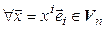 ,
, 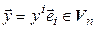 :
:


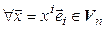 :
: 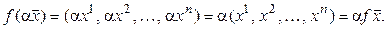
Поэтому f – линейный оператор, а значит, и изоморфизм. Итак, 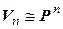 .
.
б) Пусть теперь 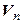 и
и  – n- мерные линейные пространства над одним и тем же полем Р. Тогда
– n- мерные линейные пространства над одним и тем же полем Р. Тогда
{ 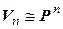 и
и 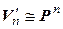 }
} 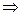 [симметричность]
[симметричность] 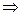 {
{ 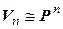 и
и 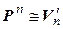 и }
и } 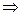
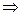 [транзитивность]
[транзитивность] 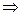 {
{ 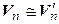 }.◄
}.◄
Таким образом, мы показали, что с точки зрения математики единственным n- мерным линейным пространством над полем Р является 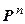 .
.



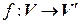 называется невырожденным, если он любой ненулевой вектор переводит в ненулевой.
называется невырожденным, если он любой ненулевой вектор переводит в ненулевой.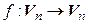 был невырожденным необходимо и достаточно, чтобы его матрица в некотором, а значит, и в любом базисе пространства
был невырожденным необходимо и достаточно, чтобы его матрица в некотором, а значит, и в любом базисе пространства 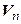 была невырожденной
была невырожденной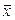 в том же базисе. Тогда
в том же базисе. Тогда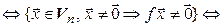
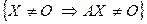
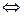
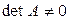 }.
}.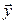 соответственно. Тогда
соответственно. Тогда невырожденный}
невырожденный} 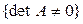
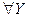 система
система 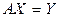 имеет единственное решение}
имеет единственное решение} 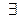 единственный
единственный 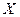 , что
, что 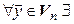 единственный
единственный 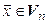 , что
, что 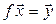 }
}  – невырожденные линейные операторы. Тогда
– невырожденные линейные операторы. Тогда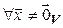 }
} 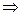 {
{ 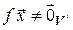 }
} 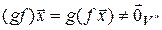 }.
}.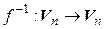 , который также является линейным. При этом, если А – матрица оператора
, который также является линейным. При этом, если А – матрица оператора 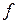 в некотором базисе, то матрица оператора
в некотором базисе, то матрица оператора  в том же базисе совпадает с матрицей
в том же базисе совпадает с матрицей 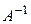 .
.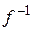 и
и 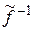 . Тогда
. Тогда
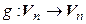 – тот линейный оператор, матрица которого в выбранном базисесовпадаетс
– тот линейный оператор, матрица которого в выбранном базисесовпадаетс 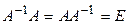 , и так как произведению матриц соответствует произведение операторов, то
, и так как произведению матриц соответствует произведение операторов, то 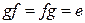 , и, таким образом,
, и, таким образом, 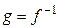 .◄
.◄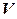 и
и 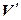 называются изоморфными. Изоморфизм обозначается так:
называются изоморфными. Изоморфизм обозначается так: 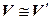 .
. – рефлективность (изоморфизм осуществляет тождественное отображение).
– рефлективность (изоморфизм осуществляет тождественное отображение).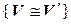
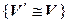 – симметричность (если первый изоморфизм осуществляет с помощью отображения f, то второй – с помощью
– симметричность (если первый изоморфизм осуществляет с помощью отображения f, то второй – с помощью  ).
). }
} 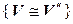 – транзитивность (если первый изоморфизм осуществляется с помощью отображения
– транзитивность (если первый изоморфизм осуществляется с помощью отображения  , то третий изоморфизм осуществляется с помощью отображения
, то третий изоморфизм осуществляется с помощью отображения 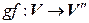 ).
).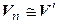 и пусть
и пусть 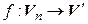 – изоморфизм. Выберем в
– изоморфизм. Выберем в 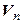 какой-либо базис
какой-либо базис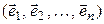 (4.27)
(4.27)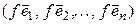 – (4.28)
– (4.28)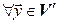
 единственный
единственный  такой, что
такой, что 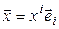 , то
, то  . Значит, (4.28) – система образующих в
. Значит, (4.28) – система образующих в 
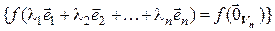
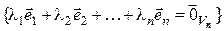
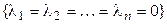
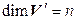 . ◄
. ◄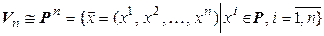 .
.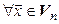 :
: 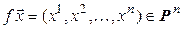 . Очевидно, отображение
. Очевидно, отображение 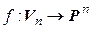 – взаимно однозначное. Кроме того,
– взаимно однозначное. Кроме того, 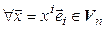 ,
, 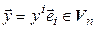 :
:

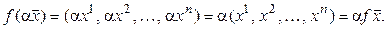
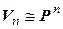 .
. – n- мерные линейные пространства над одним и тем же полем Р. Тогда
– n- мерные линейные пространства над одним и тем же полем Р. Тогда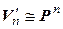 }
} 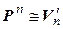 и }
и } 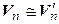 }.◄
}.◄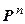 .
.


