МФЮА. МАСИ. Кафедра ОМЕНД 2015
Соболева В.В.
Математика часть 1. Линейная алгебра.
Лекция 1.
Тема 1. Векторная алгебра.
План лекции:
1. Системы координат на плоскости и в пространстве.
2. Векторы и их свойства.
3. Скалярное произведение векторов, его свойства, физический и геометрический смысл.
4. Векторное произведение векторов, его свойства, физический и геометрический смысл.
5. Смешанное произведение трех векторов, его свойства и геометрический смысл.
П.1. Системы координат на плоскости и в пространстве.
П.1.1. Системы координат на плоскости
Декартовы прямоугольные координаты (рис. 4.1)
О - начало координат, Ох - ось абсцисс, Оy - ось ординат, 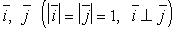 - базисные векторы,
- базисные векторы, 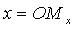 - абсцисса точки M (
- абсцисса точки M (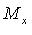 - проекция точки M на ось Ох параллельно оси Оy),
- проекция точки M на ось Ох параллельно оси Оy), 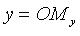 - ордината точки M (
- ордината точки M (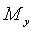 - проекция точки M на ось Oy параллельно оси Ox).
- проекция точки M на ось Oy параллельно оси Ox).
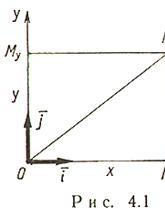
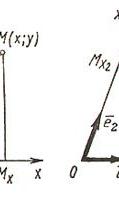
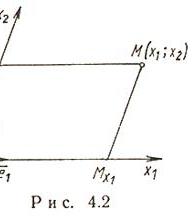
Декартовы косоугольные (афинные) координаты (рис. 4.2)
О - начало координат, 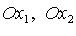 - оси координат,
- оси координат, 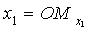 ,
, 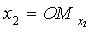 - координаты точки M (
- координаты точки M (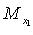 - проекция точки M на ось
- проекция точки M на ось 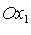 параллельно оси
параллельно оси 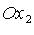 , аналогично
, аналогично 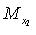 ),
), 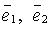 - базисные векторы.
- базисные векторы.
П.1.2.Системы координат в пространстве
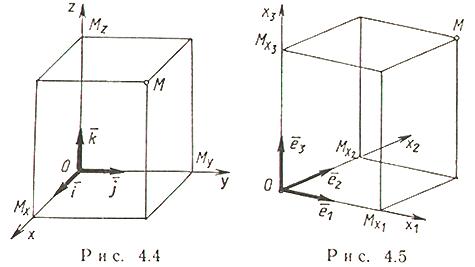
Декартовы прямоугольные координаты (рис. 4.4)
О - начало координат, Ох - ось абсцисс, Оy - ось ординат, Оz - ось аппликат, 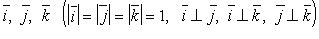 - базисные векторы. Oxy, Oxz, Oyz - координатные плоскости,
- базисные векторы. Oxy, Oxz, Oyz - координатные плоскости, 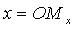 - абсцисса точки M (
- абсцисса точки M (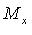 - проекция точки M на ось Ох параллельно плоскости Оyz),
- проекция точки M на ось Ох параллельно плоскости Оyz), 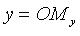 - ордината точки M (
- ордината точки M (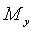 - проекция точки M на ось Oy параллельно плоскости Oxz),
- проекция точки M на ось Oy параллельно плоскости Oxz), 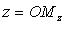 - ордината точки M (
- ордината точки M (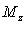 - проекция точки M на ось Oz параллельно плоскости Oxy).
- проекция точки M на ось Oz параллельно плоскости Oxy).
П.2. Векторы.
Направленный отрезок с началом в точке А и концом в точке В называется геометрическим вектором или просто вектором. Обозначается 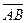 или строчными буквами латинского алфавита со стрелкой сверху:
или строчными буквами латинского алфавита со стрелкой сверху: 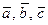 , …
, …
Длина отрезка АВ называется длиной или модулем вектора и обозначается: 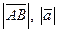 .
.
Если точки А и В совпадают, то вектор называется нулевым. Нулевой вектор обозначается либо 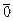 , либо 0. Нулевой вектор не имеет направления и длина его равна нулю.
, либо 0. Нулевой вектор не имеет направления и длина его равна нулю.
Два вектора называются коллинеарными, если они лежат на одной прямой или параллельны одной прямой (лежат на параллельных прямых).
Два вектора называется равными, если они коллинеарны, имеют одинаковое направление и длину.
Произведением 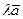 вектора
вектора 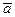 на действительное число
на действительное число 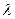 называется новый вектор
называется новый вектор 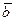 , который обладает свойствами:
, который обладает свойствами:
1о 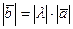 ;
;
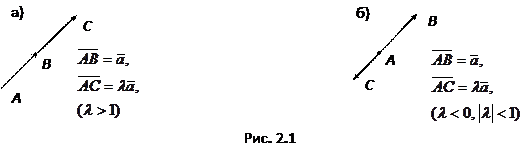
2° направление вектора 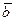 совпадает с направлением вектора
совпадает с направлением вектора 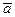 , если
, если 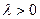
(рис. 2.1, а) и противоположно направлению вектора 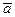 , если
, если 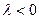 (рис. 2.1, б).
(рис. 2.1, б).
Если точка А является началом вектора 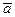 , то говорят что вектор
, то говорят что вектор 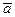 отложен от точки А. Отложим от точки А вектор
отложен от точки А. Отложим от точки А вектор 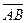 , равный
, равный 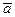 . Затем от точки В отложим вектор
. Затем от точки В отложим вектор 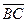 , равный
, равный 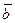 . Вектор
. Вектор 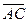 , равный
, равный 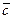 , называется суммой векторов
, называется суммой векторов 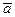 и
и 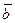 и обозначается:
и обозначается: 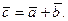
 Для любых трех точек А, В, С (рис. 2.2) справедливо равенство (правило треугольника):
Для любых трех точек А, В, С (рис. 2.2) справедливо равенство (правило треугольника):  .
.
Умножение вектора на число и сложение векторов называются линейными операциями над векторами.
Два вектора называются противоположными, если их длины равны, и они противоположно направлены. Из определения произведения вектора на число следует, что 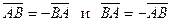 .
.
Разностью векторов 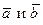 называется вектор
называется вектор 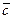 , сумма которого с вектором
, сумма которого с вектором 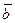 равна вектору
равна вектору 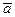 . Обозначается:
. Обозначается: 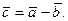 Разность векторов можно определить также равенством:
Разность векторов можно определить также равенством: 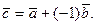 Множество всех векторов на плоскости (в пространстве) образуют линейное пространство.
Множество всех векторов на плоскости (в пространстве) образуют линейное пространство.
2.2. Проекция вектора на ось. Свойства проекций.
Единичный вектор 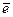 , направление которого совпадает с направлением оси 0 u, называется направляющим вектором этой оси или ортом оси. Если
, направление которого совпадает с направлением оси 0 u, называется направляющим вектором этой оси или ортом оси. Если 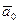 – единичный вектор, сонаправленный с вектором
– единичный вектор, сонаправленный с вектором 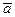 , то
, то 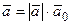 , если
, если 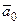 направлен противоположно вектору
направлен противоположно вектору 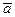 , то
, то 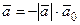 .
.
П.2.1. Понятие матрицы
Опр. 1. Прямоугольная таблица чисел, состоящая из m строк и n столбцов, называется матрицей.
Для обозначения матриц используются прописные буквы латинского алфавита: А, В, С,....
Числа, образующие матрицу, называются ее элементами. В обозначениях элементы матрицы, снабжаются двумя индексами i, j, первый индекс – номер строки, второй индекс – номер столбца, в которых находится элемент, т.е. 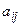 (i = 1, 2,..., m; j = 1, 2,..., n) элементы матрицы. Таким образом, полное обозначение матрицы имеет вид:
(i = 1, 2,..., m; j = 1, 2,..., n) элементы матрицы. Таким образом, полное обозначение матрицы имеет вид:
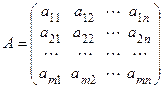 . (2.1)
. (2.1)
Для краткого обозначения матрицы будем использовать запись:
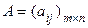 (2.2)
(2.2)
Числа m и n называются размерами матрицы, т.е. (2.1), (2.2) – записи матрицы размеров m на n (m строк и n столбцов).
Опр. 2. Если число строк матрицы совпадает с числом столбцов, т.е. m = n, то матрица называется квадратной порядка n.
Опр. 3. Матрица, в которой столбцы заменены строками, а строки столбцами, называется транспонированной и обозначается 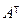 .
.
Опр. 4. Элементы квадратной матрицы с одинаковыми индексами называются главной диагональю, т.е. элементами главной диагонали будут: 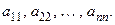
Транспонированная матрица 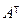 получается из матрицы А поворотом на 180° относительно главной диагонали. Например,
получается из матрицы А поворотом на 180° относительно главной диагонали. Например,
если 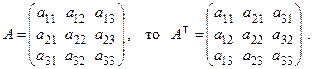
Действия над матрицами
Рассмотрим две матрицы одинаковых размеров m 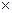 n:
n: 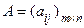 ,
, 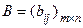 . Обозначим через I множество, состоящее из первых m чисел натурального ряда, т.е.
. Обозначим через I множество, состоящее из первых m чисел натурального ряда, т.е.
I = {1, 2,..., m}.
1. Опр.5 Матрицы А и В называются равными, если
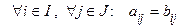 ,
,
т.e. в которых равны элементы, стоящие на одинаковых местах.
Обозначается: А = В.
2. Опр. 6. Суммой матриц А и В называется матрица 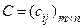 , элементы которой определяются по формулам:
, элементы которой определяются по формулам:
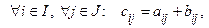
т.e. элементы матрицы С равнысумме соответствующих элементов матриц А и В.
Обозначается: С = А + В.
3. Опр. 7.Произведением матрицы А на действительное число 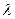 называется матрица
называется матрица 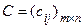 , элементы которой вычисляются по формуле:
, элементы которой вычисляются по формуле:
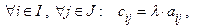
т.е. каждый элемент матрицы А умножается на число 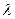 .
.
Обозначается: 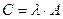 .
.
Пусть теперь 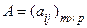 ,
, 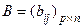 , т.е. число столбцов матрицы А совпадает с числом строк матрицы В.
, т.е. число столбцов матрицы А совпадает с числом строк матрицы В.
4. Опр8. Произведением матрицы А на матрицу В называется матрица размера m 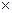 n
n 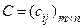 , элементы которой вычисляются по формуле:
, элементы которой вычисляются по формуле:
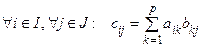 ,
,
т.е. элемент матрицы С с номерами i и j равен сумме попарных произведений элементов i-й строки матрицы А на соответствующие элементы j-го столбца матрицы В (правило «строка на столбец»). Обозначается: 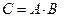 .
.
Например, если 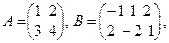 то элементы матрицы
то элементы матрицы 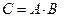 будут равны:
будут равны:
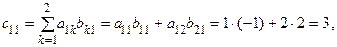
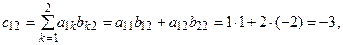
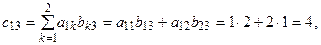
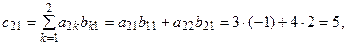
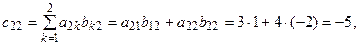
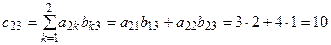 ,
,
таким образом
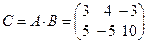 .
.
Произведение матриц не коммутативно (не перестановочно)!, т.е., вообще говоря, 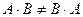 .
.
Опр. 9. если все-таки 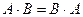 , то матрицы А и В называются перестановочными.
, то матрицы А и В называются перестановочными.
Опр.10. Квадратная матрица, у которой элементы, стоящие на главной диагонали равны 1, а все остальные равны 0, называется единичной и обозначается: Е.
Единичная матрица перестановочна с любой квадратной матрицей порядка n, так как нетрудно убедиться, что 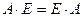 .
.
Опр.11. Определим понятие обратной матрицы. Оно определяется только для квадратных матриц. Далее А – квадратная матрица порядка n.
Матрица 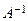 называется обратной к матрице А, если
называется обратной к матрице А, если
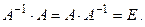
Поэтому матрицы А и 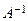 называются взаимно обратными.
называются взаимно обратными.
П.2.2. Определители.
Рассмотрим квадратную матрицу 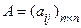 порядка n.
порядка n.
Опр. 12. Определителем или детерминантом n-го порядка матрицы А называется число 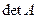
где сумма вычисляется по всем перестановкам вторых индексов. 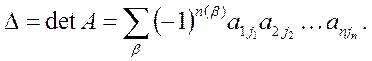 (2.3)
(2.3)
Обозначения определителя: 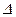 , det A, или в полной записи:
, det A, или в полной записи:
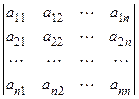 .
.
Используя определение определителя порядка n, получим формулы для вычисления определителей 2-го и 3-го порядка.
При n =2:
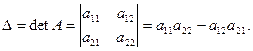 (2.4)
(2.4)
При n = 3.
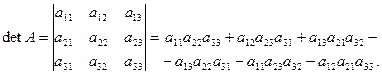 (2.5)
(2.5)
Пример
Задание. Разложив по первой строке, вычислить определитель 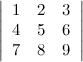
Решение. 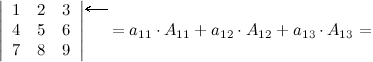
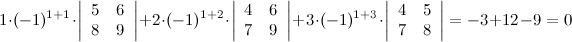
Ответ. 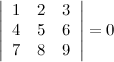
Опр. 13. Минором 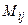 элемента
элемента 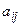 матрицы А называется определитель матрицы, полученной из матрицы А вычеркиванием i-й строки и j-гo столбца (т.е. строки и столбца, на пересечении которых находится этот элемент).
матрицы А называется определитель матрицы, полученной из матрицы А вычеркиванием i-й строки и j-гo столбца (т.е. строки и столбца, на пересечении которых находится этот элемент).
Например:
если 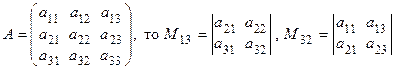 и т. д.
и т. д.
Опр. 14. (Алгебраическим дополнением 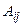 элемента
элемента 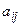 матрицы А называется число, равное
матрицы А называется число, равное 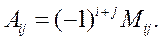
Свойства определителей
1°. Определитель матрицы А равен определителю транспонированной матрицы 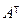 , т. е.
, т. е.
det A = det 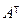 .
.
2°. Если хотя бы одна строка матрицы А состоит из нулей, то определитель этой матрицы равен нулю.
3°. °. Определитель матрицы, содержащей две одинаковые строки, равен нулю
4. При перестановке (транспозиции) любых двух строк в матрице, у определителя этой матрицы изменится знак.
5°. Если все элементы некоторой строки матрицы умножить на действительное число 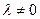 , то определитель этой матрицы умножится на
, то определитель этой матрицы умножится на 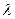 .
.
6°. Пусть матрицы А, В, С отличаются друг от друга только k-й строкой, причем элементы k-й строки матрицы С равны сумме соответствующих элементов k-х строк матриц А и В т.е.
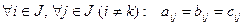
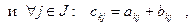
тогда 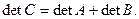
7°. Определитель матрицы не изменится, если к элементам какой-либо строки прибавить соответствующие элементы другой строки, умноженные на число 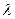 .(8°. (Теорема аннулирования). Сумма произведений элементов, какой либо строки на алгебраические дополнения соответствующих элементов другой строки равна нулю, т.е.
.(8°. (Теорема аннулирования). Сумма произведений элементов, какой либо строки на алгебраические дополнения соответствующих элементов другой строки равна нулю, т.е. 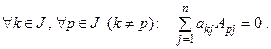 ) (2.7)
) (2.7)
Опр. 15. Матрица называется невырожденной, если 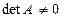 , и вырожденной в противном случае.
, и вырожденной в противном случае.
Определитель выгоднее раскрывать по ТОЙ строке (столбцу), где:
1) нулей побольше;
2) числа поменьше.
1.Вычислить определитель 2на 2.
2.3 на 3
1.Вычислить определитель 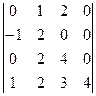
2.3 Обратная матрица.
Рассмотрим квадратную матрицу 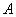 . Обратную матрицу . Обратную матрицу 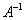 можно найти по следующей формуле: можно найти по следующей формуле:
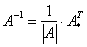 , где , где 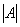 – определитель матрицы – определитель матрицы 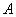 , , 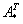 – транспонированная матрица алгебраических дополнений соответствующих элементов матрицы – транспонированная матрица алгебраических дополнений соответствующих элементов матрицы 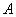 .
Понятие обратной матрицы существует только для квадратных матриц, матриц «два на два», «три на три» и т.д.
Пример 1:
Найти обратную матрицу для матрицы .
Понятие обратной матрицы существует только для квадратных матриц, матриц «два на два», «три на три» и т.д.
Пример 1:
Найти обратную матрицу для матрицы 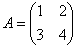 Решаем. Последовательность действий удобно разложить по пунктам.
1) Сначала находим определитель матрицы.
Решаем. Последовательность действий удобно разложить по пунктам.
1) Сначала находим определитель матрицы.
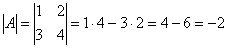 Важно! В том случае, если определитель матрицы равен НУЛЮ – обратной матрицы НЕ СУЩЕСТВУЕТ.
В рассматриваемом примере, как выяснилось,
Важно! В том случае, если определитель матрицы равен НУЛЮ – обратной матрицы НЕ СУЩЕСТВУЕТ.
В рассматриваемом примере, как выяснилось, 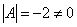 , а значит, всё в порядке.
2) Находим матрицу миноров , а значит, всё в порядке.
2) Находим матрицу миноров 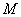 .
Матрица миноров имеет такие же размеры, как и матрица .
Матрица миноров имеет такие же размеры, как и матрица 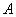 , то есть в данном случае , то есть в данном случае 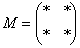 . Дело за малым, осталось найти четыре числа и поставить их вместо звездочек.
Возвращаемся к нашей матрице . Дело за малым, осталось найти четыре числа и поставить их вместо звездочек.
Возвращаемся к нашей матрице 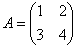 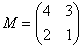 – матрица миноров соответствующих элементов матрицы – матрица миноров соответствующих элементов матрицы 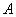 .
3) Находим матрицу алгебраических дополнений .
3) Находим матрицу алгебраических дополнений 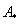 .
Это просто. В матрице миноров нужно ПОМЕНЯТЬ ЗНАКИ у двух чисел: .
Это просто. В матрице миноров нужно ПОМЕНЯТЬ ЗНАКИ у двух чисел: 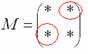 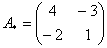 – матрица алгебраических дополнений соответствующих элементов матрицы – матрица алгебраических дополнений соответствующих элементов матрицы 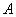 .
4) Находим транспонированную матрицу алгебраических дополнений .
4) Находим транспонированную матрицу алгебраических дополнений 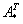 . .
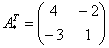 – транспонированная матрица алгебраических дополнений соответствующих элементов матрицы – транспонированная матрица алгебраических дополнений соответствующих элементов матрицы 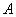 .
5) Ответ. Вспоминаем нашу формулу .
5) Ответ. Вспоминаем нашу формулу 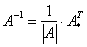 Таким образом, обратная матрица:
Таким образом, обратная матрица: 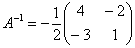 Как проверить решение?
Необходимо выполнить матричное умножение
Как проверить решение?
Необходимо выполнить матричное умножение 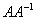 либо либо 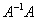 Получена так называемая единичная матрица (с единицами по главной диагонали и нулями в остальных местах).
Таким образом, обратная матрица найдена правильно.
Если провести действие
Получена так называемая единичная матрица (с единицами по главной диагонали и нулями в остальных местах).
Таким образом, обратная матрица найдена правильно.
Если провести действие 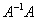 , то в результате тоже получится единичная матрица. Это один из немногих случаев, когда умножение матриц перестановочно. , то в результате тоже получится единичная матрица. Это один из немногих случаев, когда умножение матриц перестановочно.
|
2.4. Ранг матрицы
Рассмотрим прямоугольную матрицу 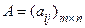 . Выберем в матрице А произвольно k строк с номерами i1, i2, …, ik и k столбцов с номерами j1, j2,..., jk, . Выберем в матрице А произвольно k строк с номерами i1, i2, …, ik и k столбцов с номерами j1, j2,..., jk, 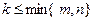 . Элементы, стоящие на пересечении выбранных строк и столбцов, образуют квадратную матрицу Аk порядка k.
Как мы уже знаем, определитель матрицы Аk называется минором k-гo порядка (минором порядка k) и обозначается . Элементы, стоящие на пересечении выбранных строк и столбцов, образуют квадратную матрицу Аk порядка k.
Как мы уже знаем, определитель матрицы Аk называется минором k-гo порядка (минором порядка k) и обозначается 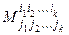 или, когда не важно, какие именно строки и столбцы выбраны, обозначается Mk, т.е. по определению Mk = det Аk. Например, если или, когда не важно, какие именно строки и столбцы выбраны, обозначается Mk, т.е. по определению Mk = det Аk. Например, если
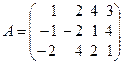 и выбраны строки c номерами i1 = 1, i2 = 3 и столбцы с номерами j1 = 2, j2 = 4, то
и выбраны строки c номерами i1 = 1, i2 = 3 и столбцы с номерами j1 = 2, j2 = 4, то
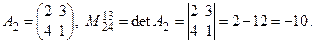 Число миноров второго порядка для этой матрицы равно 18.
Опр.16.Наивысший порядок миноров, не равных нулю, называется рангом матрицы и обозначается символами: rаng А или rA.
Из этого определения легко получить следующее правило для нахождения ранга матрицы: если найден минор порядка r не равный нулю и любой минор порядка r + 1 равен нулю, то ранг матрицы А равен r.
Пример 1.2. Найти ранг матрицы:
Число миноров второго порядка для этой матрицы равно 18.
Опр.16.Наивысший порядок миноров, не равных нулю, называется рангом матрицы и обозначается символами: rаng А или rA.
Из этого определения легко получить следующее правило для нахождения ранга матрицы: если найден минор порядка r не равный нулю и любой минор порядка r + 1 равен нулю, то ранг матрицы А равен r.
Пример 1.2. Найти ранг матрицы:
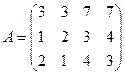 .
Решение. Здесь .
Решение. Здесь 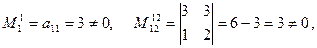
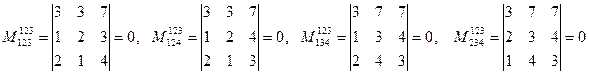 ,
следовательно rаng А = 2.
Вычисление ранга матрицы по определению приводит к очень громоздким и длительным вычислениям, поэтому чаще всего он вычисляется с помощью элементарных преобразований матрицы.
Элементарные преобразования матрицы:
1) перестановка (транспозиция) строк (столбцов) матрицы;
2) умножение всех элементов отроки (столбца) матрицы на действительное число ,
следовательно rаng А = 2.
Вычисление ранга матрицы по определению приводит к очень громоздким и длительным вычислениям, поэтому чаще всего он вычисляется с помощью элементарных преобразований матрицы.
Элементарные преобразования матрицы:
1) перестановка (транспозиция) строк (столбцов) матрицы;
2) умножение всех элементов отроки (столбца) матрицы на действительное число 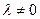 ;
3) прибавление к элементам строки (столбца) матрицы соответствующих элементов другой строки (столбца), умноженных на действительное число.
Утверждение 2.2. Элементарные преобразования не изменяют ранга матрицы. ;
3) прибавление к элементам строки (столбца) матрицы соответствующих элементов другой строки (столбца), умноженных на действительное число.
Утверждение 2.2. Элементарные преобразования не изменяют ранга матрицы.
|
П.6.5. Угол между прямыми.
П.6.6. Кривые на плоскости.
П.6.1. Прямые на плоскости.
Обозначения: прямые обозначаются маленькими латинскими буквами: 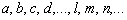 .
.
Поскольку любая прямая однозначно определяется двумя точками, то её можно обозначать данными точками: 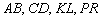 и т.д.
и т.д.
Обозначение 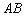 совершенно очевидно подразумевает, что точки
совершенно очевидно подразумевает, что точки 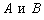 принадлежат прямой
принадлежат прямой 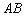 .
.
1.Уравнение прямой по угловому коэффициенту и точке:
Если известна точка 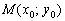 , принадлежащая некоторой прямой, и угловой коэффициент
, принадлежащая некоторой прямой, и угловой коэффициент 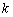 этой прямой, то уравнение данной прямой выражается формулой:
этой прямой, то уравнение данной прямой выражается формулой:
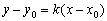
Пример 1. Составить уравнение прямой с угловым коэффициентом 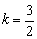 , если известно, что точка
, если известно, что точка 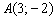 принадлежит данной прямой.
принадлежит данной прямой.
Решение: Уравнение прямой составим по формуле 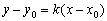 .
.
В данном случае:
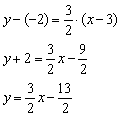
Ответ: 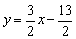
2.Общее уравнение прямой: 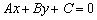 , где
, где 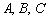 – некоторые числа.
– некоторые числа.
При этом коэффициенты 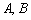 одновременно не равны нулю, так как уравнение теряет смысл.
одновременно не равны нулю, так как уравнение теряет смысл.
От предыдущей формы уравнения прямой с угловым коэффициентом к общей форме прямой перейти просто:
Например у нас есть уравнение с угловым коэффициентом 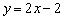
Меняем знаки:
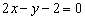 .
.
Запомните! Первый коэффициент (чаще всего 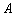 ) делаем положительным!
) делаем положительным!
В аналитической геометрии уравнение прямой почти всегда будет задано в общей форме.
Ну, а при необходимости его легко привести к «школьному» виду с угловым коэффициентом 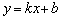 (за исключением прямых, параллельных оси ординат).
(за исключением прямых, параллельных оси ординат).
Переходим к третьему виду уравнения прямой. Мы можем описать прямую, зная ее наклон по отношению, например, к оси X. У каждой прямой есть вполне определённый наклон, который, как мы знаем из Лекции1, может быть описан вектором.
Опр. 6.1. Вектор, который параллелен прямой, называется направляющим вектором данной прямой.
Очевидно, что у любой прямой бесконечно много направляющих векторов, причём все они будут коллинеарны (сонаправлены или нет – неважно).
Направляющий вектор будем обозначать следующим образом: 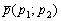 .
.
Но одного вектора недостаточно для построения прямой, вектор является свободным и не привязан к какой-либо точке плоскости. Поэтому дополнительно необходимо знать некоторую точку 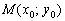 , которая принадлежит прямой.
, которая принадлежит прямой.
3.Уравнение прямой по точке и направляющему вектору:
Если известна некоторая точка 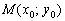 , принадлежащая прямой, и направляющий вектор
, принадлежащая прямой, и направляющий вектор 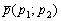 этой прямой, то уравнение данной прямой можно составить по формуле:
этой прямой, то уравнение данной прямой можно составить по формуле:
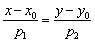
Иногда его называют каноническим уравнением прямой.
Пример 2.
Составить уравнение прямой по точке 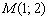 и направляющему вектору
и направляющему вектору 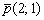
Решение: Уравнение прямой составим по формуле 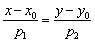 . В данном случае:
. В данном случае:
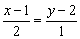
С помощью свойств пропорции избавляемся от дробей:
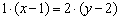
И приводим уравнение к общему виду:
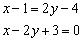
Ответ: 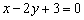
Пример 3.
Примеры нахождения направляющих векторов прямых:
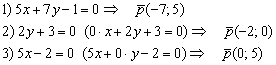
Утверждение позволяет найти лишь один направляющий вектор из бесчисленного множества, но нам больше и не нужно. Хотя в ряде случаев координаты направляющих векторов целесообразно сократить:
Так, уравнение 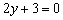 задаёт прямую, которая параллельна оси
задаёт прямую, которая параллельна оси 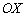 и координаты полученного направляющего вектора
и координаты полученного направляющего вектора 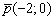 удобно разделить на –2, получая в точности базисный вектор
удобно разделить на –2, получая в точности базисный вектор 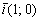 в качестве направляющего вектора. Логично.
в качестве направляющего вектора. Логично.
Пример 4
Составить уравнение прямой по точке 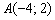 и направляющему вектору
и направляющему вектору 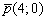 .
.
Решение: Формула 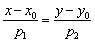 не годится, так как знаменатель правой части равен нулю. Выход есть! Используя свойства пропорции, перепишем формулу в виде
не годится, так как знаменатель правой части равен нулю. Выход есть! Используя свойства пропорции, перепишем формулу в виде 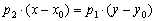 , и дальнейшее покатилось по глубокой колее:
, и дальнейшее покатилось по глубокой колее:
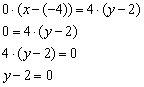
Ответ: 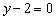
Далее, перейдем к новому виду уравнения прямой – по двум точкам.
Пример 6.
Составить уравнение прямой по точке 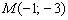 и вектору нормали
и вектору нормали 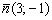 . Найти направляющий вектор прямой.
. Найти направляющий вектор прямой.
Решение: Используем формулу:
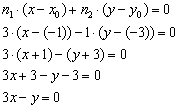
Общее уравнение прямой получено:
Ответ: 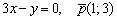
На чертеже ситуация выглядит следующим образом:
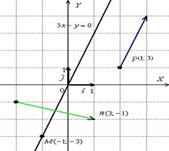
Далее рассмотрим уравнение прямой в отрезках:
1. Уравнение прямой в отрезках имеет вид 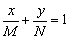 , где
, где 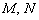 – ненулевые константы.
– ненулевые константы.
Некоторые типы уравнений нельзя представить в таком виде, например, прямую пропорциональность 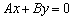 (так как свободный член
(так как свободный член 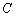 равен нулю и единицу в правой части никак не получить).
равен нулю и единицу в правой части никак не получить).
Пример 7
Дана прямая 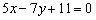 . Составить уравнение прямой в отрезках и определить точки пересечения графика с координатными осями.
. Составить уравнение прямой в отрезках и определить точки пересечения графика с координатными осями.
Решение: Приведём уравнение к виду 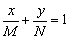 . Сначала перенесём свободный член в правую часть:
. Сначала перенесём свободный член в правую часть:
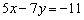
Чтобы получить справа единицу, разделим каждый член уравнения на –11:
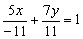
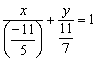
Таким образом, точки пересечения прямой с координатными осями:
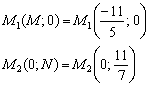
Ответ: 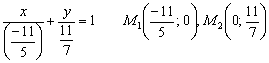
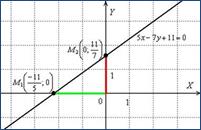
Легко усмотреть, что данная прямая однозначно определяется красным и зелёным отрезками, отсюда и название – «уравнение прямой в отрезках».
Пример 8
Составить параметрические уравнения прямой по точке 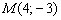 и направляющему вектору
и направляющему вектору 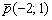
Решение:
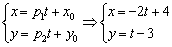
Пример 10.
Рассмотрим прямые 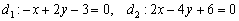 и составим три уравнения из соответствующих коэффициентов:
и составим три уравнения из соответствующих коэффициентов: 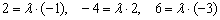 . Из каждого уравнения следует, что
. Из каждого уравнения следует, что 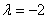 , следовательно, данные прямые совпадают.
, следовательно, данные прямые совпадают.
Второй случай, когда прямые параллельны:
Теорема 2. Две прямые параллельны тогда и только тогда, когда их коэффициенты при переменных 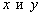 пропорциональны:
пропорциональны: 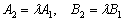 , но
, но 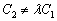 .
.
Пример 11.
В качестве примера рассмотрим две прямые 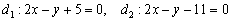 . Проверяем пропорциональность соответствующих коэффициентов при переменных
. Проверяем пропорциональность соответствующих коэффициентов при переменных 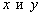 :
:
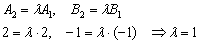
Однако совершенно очевидно, что 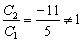 .
.
Вывод: 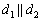
И третий случай, когда прямые пересекаются:
Теорема 3. Две прямые пересекаются, тогда и только тогда, когда их коэффициенты при переменных 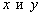 НЕ пропорциональны, то есть НЕ существует такого значения «лямбда», чтобы выполнялись равенства
НЕ пропорциональны, то есть НЕ существует такого значения «лямбда», чтобы выполнялись равенства 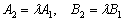
Так, для прямых 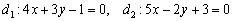 составим систему:
составим систему:
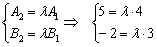
Из первого уравнения следует, что 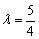 , а из второго уравнения:
, а из второго уравнения: 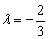 , значит, система несовместна (решений нет). Таким образом, коэффициенты при переменных
, значит, система несовместна (решений нет). Таким образом, коэффициенты при переменных 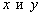 не пропорциональны.
не пропорциональны.
Вывод: прямые пересекаются
Пример 12.
Выяснить взаимное расположение прямых:
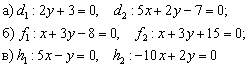
Решение основано на исследовании направляющих векторов прямых:
а) Из уравнений 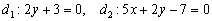 найдём направляющие векторы прямых:
найдём направляющие векторы прямых: 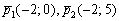 .
.
Вычислим определитель, составленный из координат данных векторов:
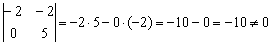 , значит, векторы
, значит, векторы 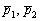 не коллинеарны и прямые
не коллинеарны и прямые 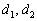 пересекаются.
пересекаются.
б) Найдем направляющие векторы прямых 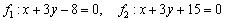 :
:
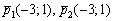
Прямые имеют один и тот же направляющий вектор, значит, они либо параллельны, либо совпадают. Тут и определитель считать не надо.
Очевидно, что коэффициенты при неизвестных 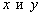 пропорциональны, при этом
пропорциональны, при этом 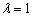 .
.
Выясним, справедливо ли равенство 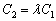 :
:
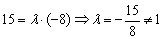
Таким образом, 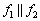
в) Найдем направляющие векторы прямых 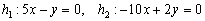 :
:
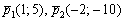
Вычислим определитель, составленный из координат данных векторов:
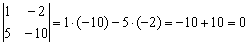 , следовательно, направляющие векторы коллинеарны. Прямые либо параллельны либо совпадают.
, следовательно, направляющие векторы коллинеарны. Прямые либо параллельны либо совпадают.
Коэффициент пропорциональности «лямбда» можно узнать прямо соотношения коллинеарных направляющих векторов 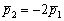 . Впрочем, можно и через коэффициенты самих уравнений:
. Впрочем, можно и через коэффициенты самих уравнений: 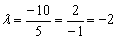 .
.
Теперь выясним, справедливо ли равенство 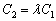 . Оба свободных члена нулевые, поэтому:
. Оба свободных члена нулевые, поэтому:
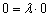
Полученное значение 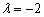 удовлетворяет данному уравнению (ему удовлетворяет вообще любое число).
удовлетворяет данному уравнению (ему удовлетворяет вообще любое число).
Таким образом, прямые совпадают.
Ответ: 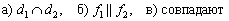 .
.
Пример 13.
Найти точку пересечения прямых 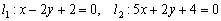
Решение: Точку пересечения 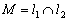 целесообразно искать аналитическим методом. Решим систему:
целесообразно искать аналитическим методом. Решим систему:
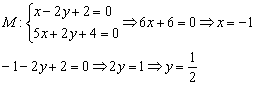
Ответ: 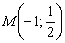
Пример 14.
Найти расстояние от точки 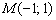 до прямой
до прямой 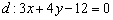
Решение: всё что нужно - аккуратно подставить числа в формулу и провести вычисления:
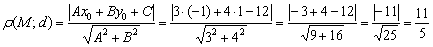
Ответ: 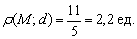
П.6.5. Угол между прямыми.
Пример 15.
Найти угол между прямыми 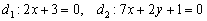 .
.
1. Проверяем перпендикулярны ли прямые:
Вычислим скалярное произведение направляющих векторов прямых:
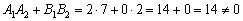 , значит, прямые не перпендикулярны.
, значит, прямые не перпендикулярны.
2. Угол между прямыми найдём с помощью формулы:
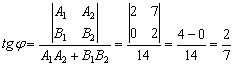
Таким образом:
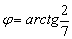
Ответ: 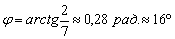
Эллипс.
Эллипсом называется множество точек на плоскости, для каждой из которых сумма расстояний до двух данных точек есть величина постоянная (причем эта величина больше расстояний между данными точками). Данные точки называются фокусами эллипса.
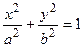
– каноническое уравнение эллипса.
Отношение 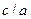 называется эксцентриситетом эллипса и обозначается:
называется эксцентриситетом эллипса и обозначается: 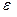 ,
, 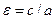 . Так как
. Так как 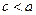 , то
, то 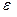 < 1.
< 1.
Следовательно, с уменьшением 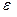 отношение
отношение 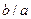 стремится к 1, т.е. b мало отличается от а и форма эллипса становится ближе к форме окружности. В предельном случае при
стремится к 1, т.е. b мало отличается от а и форма эллипса становится ближе к форме окружности. В предельном случае при 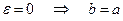 , получается окружность, уравнение которой есть
, получается окружность, уравнение которой есть
х2 + у2 = а2.
Гипербола
Гиперболой называется множество точек на плоскости, для каждой из которых абс



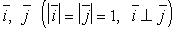 - базисные векторы,
- базисные векторы, 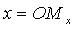 - абсцисса точки M (
- абсцисса точки M (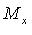 - проекция точки M на ось Ох параллельно оси Оy),
- проекция точки M на ось Ох параллельно оси Оy), 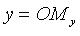 - ордината точки M (
- ордината точки M (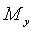 - проекция точки M на ось Oy параллельно оси Ox).
- проекция точки M на ось Oy параллельно оси Ox).


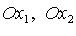 - оси координат,
- оси координат, 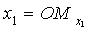 ,
, 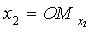 - координаты точки M (
- координаты точки M (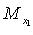 - проекция точки M на ось
- проекция точки M на ось 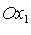 параллельно оси
параллельно оси 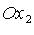 , аналогично
, аналогично 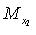 ),
), 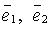 - базисные векторы.
- базисные векторы.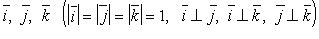 - базисные векторы. Oxy, Oxz, Oyz - координатные плоскости,
- базисные векторы. Oxy, Oxz, Oyz - координатные плоскости, 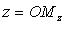 - ордината точки M (
- ордината точки M (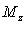 - проекция точки M на ось Oz параллельно плоскости Oxy).
- проекция точки M на ось Oz параллельно плоскости Oxy).
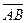 или строчными буквами латинского алфавита со стрелкой сверху:
или строчными буквами латинского алфавита со стрелкой сверху: 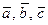 , …
, …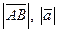 .
.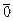 , либо 0. Нулевой вектор не имеет направления и длина его равна нулю.
, либо 0. Нулевой вектор не имеет направления и длина его равна нулю.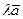 вектора
вектора 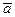 на действительное число
на действительное число 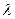 называется новый вектор
называется новый вектор 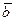 , который обладает свойствами:
, который обладает свойствами: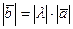 ;
;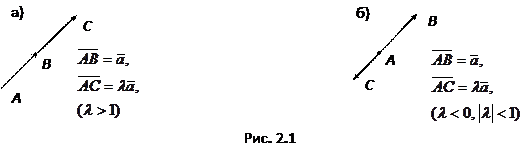
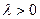
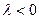 (рис. 2.1, б).
(рис. 2.1, б).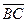 , равный
, равный 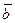 . Вектор
. Вектор 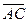 , равный
, равный 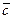 , называется суммой векторов
, называется суммой векторов 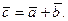
 Для любых трех точек А, В, С (рис. 2.2) справедливо равенство (правило треугольника):
Для любых трех точек А, В, С (рис. 2.2) справедливо равенство (правило треугольника):  .
.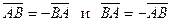 .
.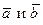 называется вектор
называется вектор 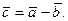 Разность векторов можно определить также равенством:
Разность векторов можно определить также равенством: 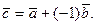 Множество всех векторов на плоскости (в пространстве) образуют линейное пространство.
Множество всех векторов на плоскости (в пространстве) образуют линейное пространство.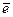 , направление которого совпадает с направлением оси 0 u, называется направляющим вектором этой оси или ортом оси. Если
, направление которого совпадает с направлением оси 0 u, называется направляющим вектором этой оси или ортом оси. Если 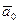 – единичный вектор, сонаправленный с вектором
– единичный вектор, сонаправленный с вектором 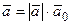 , если
, если 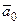 направлен противоположно вектору
направлен противоположно вектору 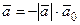 .
.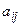 (i = 1, 2,..., m; j = 1, 2,..., n) элементы матрицы. Таким образом, полное обозначение матрицы имеет вид:
(i = 1, 2,..., m; j = 1, 2,..., n) элементы матрицы. Таким образом, полное обозначение матрицы имеет вид: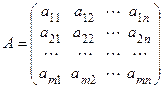 . (2.1)
. (2.1)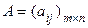 (2.2)
(2.2)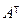 .
.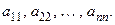
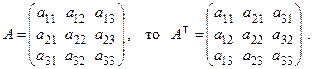
 n:
n: 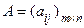 ,
, 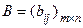 . Обозначим через I множество, состоящее из первых m чисел натурального ряда, т.е.
. Обозначим через I множество, состоящее из первых m чисел натурального ряда, т.е.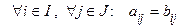 ,
,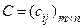 , элементы которой определяются по формулам:
, элементы которой определяются по формулам: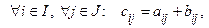
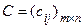 , элементы которой вычисляются по формуле:
, элементы которой вычисляются по формуле: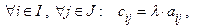
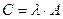 .
.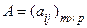 ,
, 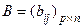 , т.е. число столбцов матрицы А совпадает с числом строк матрицы В.
, т.е. число столбцов матрицы А совпадает с числом строк матрицы В.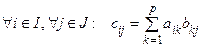 ,
,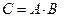 .
.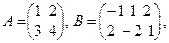 то элементы матрицы
то элементы матрицы 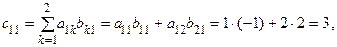
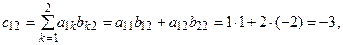
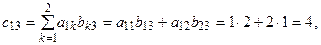
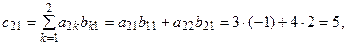
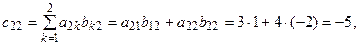
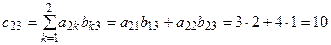 ,
,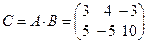 .
.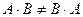 .
.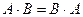 , то матрицы А и В называются перестановочными.
, то матрицы А и В называются перестановочными.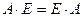 .
.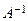 называется обратной к матрице А, если
называется обратной к матрице А, если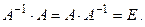
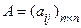 порядка n.
порядка n.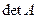
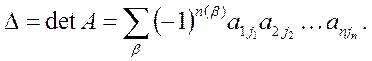 (2.3)
(2.3)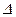 , det A, или в полной записи:
, det A, или в полной записи: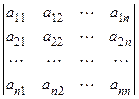 .
.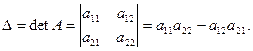 (2.4)
(2.4)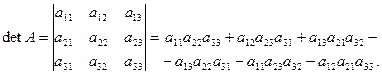 (2.5)
(2.5)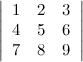
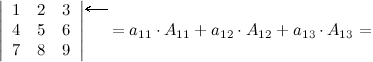
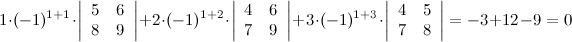
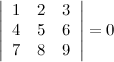
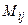 элемента
элемента 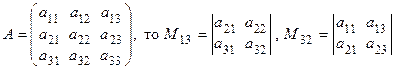 и т. д.
и т. д.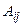 элемента
элемента 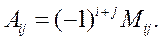
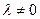 , то определитель этой матрицы умножится на
, то определитель этой матрицы умножится на 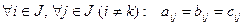
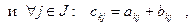
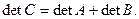
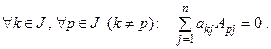 ) (2.7)
) (2.7)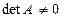 , и вырожденной в противном случае.
, и вырожденной в противном случае.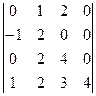
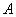 . Обратную матрицу
. Обратную матрицу 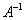 можно найти по следующей формуле:
можно найти по следующей формуле:
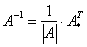 , где
, где 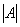 – определитель матрицы
– определитель матрицы 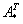 – транспонированная матрица алгебраических дополнений соответствующих элементов матрицы
– транспонированная матрица алгебраических дополнений соответствующих элементов матрицы 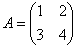 Решаем. Последовательность действий удобно разложить по пунктам.
1) Сначала находим определитель матрицы.
Решаем. Последовательность действий удобно разложить по пунктам.
1) Сначала находим определитель матрицы.
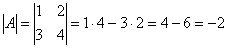 Важно! В том случае, если определитель матрицы равен НУЛЮ – обратной матрицы НЕ СУЩЕСТВУЕТ.
В рассматриваемом примере, как выяснилось,
Важно! В том случае, если определитель матрицы равен НУЛЮ – обратной матрицы НЕ СУЩЕСТВУЕТ.
В рассматриваемом примере, как выяснилось, 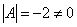 , а значит, всё в порядке.
2) Находим матрицу миноров
, а значит, всё в порядке.
2) Находим матрицу миноров 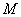 .
Матрица миноров имеет такие же размеры, как и матрица
.
Матрица миноров имеет такие же размеры, как и матрица 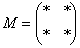 . Дело за малым, осталось найти четыре числа и поставить их вместо звездочек.
Возвращаемся к нашей матрице
. Дело за малым, осталось найти четыре числа и поставить их вместо звездочек.
Возвращаемся к нашей матрице 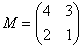 – матрица миноров соответствующих элементов матрицы
– матрица миноров соответствующих элементов матрицы 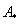 .
Это просто. В матрице миноров нужно ПОМЕНЯТЬ ЗНАКИ у двух чисел:
.
Это просто. В матрице миноров нужно ПОМЕНЯТЬ ЗНАКИ у двух чисел: 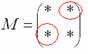
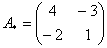 – матрица алгебраических дополнений соответствующих элементов матрицы
– матрица алгебраических дополнений соответствующих элементов матрицы 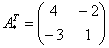 – транспонированная матрица алгебраических дополнений соответствующих элементов матрицы
– транспонированная матрица алгебраических дополнений соответствующих элементов матрицы 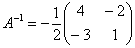 Как проверить решение?
Необходимо выполнить матричное умножение
Как проверить решение?
Необходимо выполнить матричное умножение 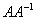 либо
либо 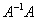 Получена так называемая единичная матрица (с единицами по главной диагонали и нулями в остальных местах).
Таким образом, обратная матрица найдена правильно.
Если провести действие
Получена так называемая единичная матрица (с единицами по главной диагонали и нулями в остальных местах).
Таким образом, обратная матрица найдена правильно.
Если провести действие 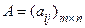 . Выберем в матрице А произвольно k строк с номерами i1, i2, …, ik и k столбцов с номерами j1, j2,..., jk,
. Выберем в матрице А произвольно k строк с номерами i1, i2, …, ik и k столбцов с номерами j1, j2,..., jk, 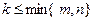 . Элементы, стоящие на пересечении выбранных строк и столбцов, образуют квадратную матрицу Аk порядка k.
Как мы уже знаем, определитель матрицы Аk называется минором k-гo порядка (минором порядка k) и обозначается
. Элементы, стоящие на пересечении выбранных строк и столбцов, образуют квадратную матрицу Аk порядка k.
Как мы уже знаем, определитель матрицы Аk называется минором k-гo порядка (минором порядка k) и обозначается 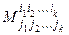 или, когда не важно, какие именно строки и столбцы выбраны, обозначается Mk, т.е. по определению Mk = det Аk. Например, если
или, когда не важно, какие именно строки и столбцы выбраны, обозначается Mk, т.е. по определению Mk = det Аk. Например, если
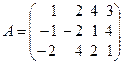 и выбраны строки c номерами i1 = 1, i2 = 3 и столбцы с номерами j1 = 2, j2 = 4, то
и выбраны строки c номерами i1 = 1, i2 = 3 и столбцы с номерами j1 = 2, j2 = 4, то
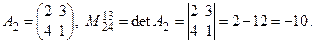 Число миноров второго порядка для этой матрицы равно 18.
Опр.16.Наивысший порядок миноров, не равных нулю, называется рангом матрицы и обозначается символами: rаng А или rA.
Из этого определения легко получить следующее правило для нахождения ранга матрицы: если найден минор порядка r не равный нулю и любой минор порядка r + 1 равен нулю, то ранг матрицы А равен r.
Пример 1.2. Найти ранг матрицы:
Число миноров второго порядка для этой матрицы равно 18.
Опр.16.Наивысший порядок миноров, не равных нулю, называется рангом матрицы и обозначается символами: rаng А или rA.
Из этого определения легко получить следующее правило для нахождения ранга матрицы: если найден минор порядка r не равный нулю и любой минор порядка r + 1 равен нулю, то ранг матрицы А равен r.
Пример 1.2. Найти ранг матрицы:
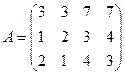 .
Решение. Здесь
.
Решение. Здесь 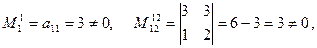
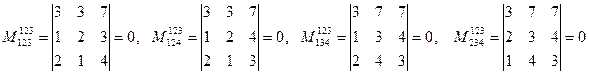 ,
следовательно rаng А = 2.
Вычисление ранга матрицы по определению приводит к очень громоздким и длительным вычислениям, поэтому чаще всего он вычисляется с помощью элементарных преобразований матрицы.
Элементарные преобразования матрицы:
1) перестановка (транспозиция) строк (столбцов) матрицы;
2) умножение всех элементов отроки (столбца) матрицы на действительное число
,
следовательно rаng А = 2.
Вычисление ранга матрицы по определению приводит к очень громоздким и длительным вычислениям, поэтому чаще всего он вычисляется с помощью элементарных преобразований матрицы.
Элементарные преобразования матрицы:
1) перестановка (транспозиция) строк (столбцов) матрицы;
2) умножение всех элементов отроки (столбца) матрицы на действительное число 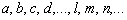 .
.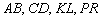 и т.д.
и т.д.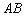 совершенно очевидно подразумевает, что точки
совершенно очевидно подразумевает, что точки 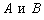 принадлежат прямой
принадлежат прямой 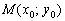 , принадлежащая некоторой прямой, и угловой коэффициент
, принадлежащая некоторой прямой, и угловой коэффициент 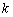 этой прямой, то уравнение данной прямой выражается формулой:
этой прямой, то уравнение данной прямой выражается формулой: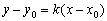
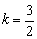 , если известно, что точка
, если известно, что точка 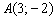 принадлежит данной прямой.
принадлежит данной прямой.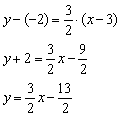
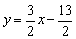
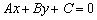 , где
, где 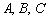 – некоторые числа.
– некоторые числа.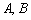 одновременно не равны нулю, так как уравнение теряет смысл.
одновременно не равны нулю, так как уравнение теряет смысл.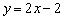
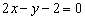 .
.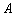 ) делаем положительным!
) делаем положительным!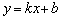 (за исключением прямых, параллельных оси ординат).
(за исключением прямых, параллельных оси ординат).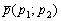 .
.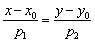
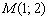 и направляющему вектору
и направляющему вектору 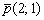
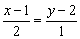
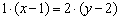
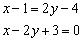
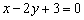
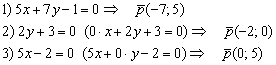
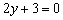 задаёт прямую, которая параллельна оси
задаёт прямую, которая параллельна оси 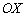 и координаты полученного направляющего вектора
и координаты полученного направляющего вектора 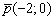 удобно разделить на –2, получая в точности базисный вектор
удобно разделить на –2, получая в точности базисный вектор 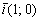 в качестве направляющего вектора. Логично.
в качестве направляющего вектора. Логично.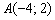 и направляющему вектору
и направляющему вектору 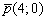 .
.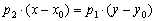 , и дальнейшее покатилось по глубокой колее:
, и дальнейшее покатилось по глубокой колее: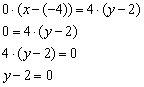
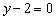
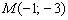 и вектору нормали
и вектору нормали 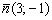 . Найти направляющий вектор прямой.
. Найти направляющий вектор прямой.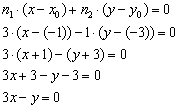
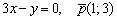

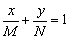 , где
, где 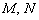 – ненулевые константы.
– ненулевые константы.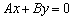 (так как свободный член
(так как свободный член 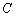 равен нулю и единицу в правой части никак не получить).
равен нулю и единицу в правой части никак не получить).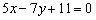 . Составить уравнение прямой в отрезках и определить точки пересечения графика с координатными осями.
. Составить уравнение прямой в отрезках и определить точки пересечения графика с координатными осями.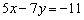
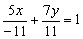
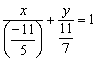
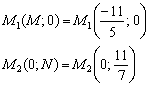
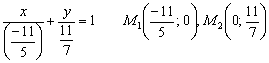

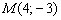 и направляющему вектору
и направляющему вектору 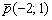
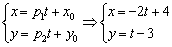
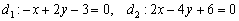 и составим три уравнения из соответствующих коэффициентов:
и составим три уравнения из соответствующих коэффициентов: 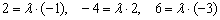 . Из каждого уравнения следует, что
. Из каждого уравнения следует, что 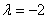 , следовательно, данные прямые совпадают.
, следовательно, данные прямые совпадают.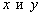 пропорциональны:
пропорциональны: 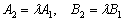 , но
, но 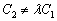 .
.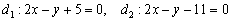 . Проверяем пропорциональность соответствующих коэффициентов при переменных
. Проверяем пропорциональность соответствующих коэффициентов при переменных 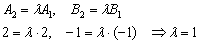
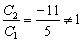 .
.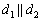
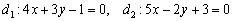 составим систему:
составим систему: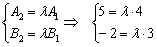
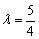 , а из второго уравнения:
, а из второго уравнения: 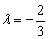 , значит, система несовместна (решений нет). Таким образом, коэффициенты при переменных
, значит, система несовместна (решений нет). Таким образом, коэффициенты при переменных 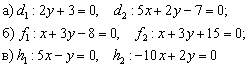
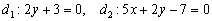 найдём направляющие векторы прямых:
найдём направляющие векторы прямых: 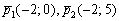 .
.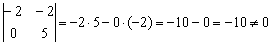 , значит, векторы
, значит, векторы 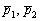 не коллинеарны и прямые
не коллинеарны и прямые 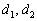 пересекаются.
пересекаются.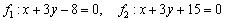 :
: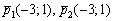
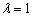 .
.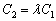 :
: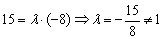
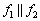
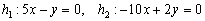 :
: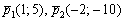
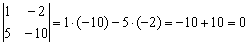 , следовательно, направляющие векторы коллинеарны. Прямые либо параллельны либо совпадают.
, следовательно, направляющие векторы коллинеарны. Прямые либо параллельны либо совпадают.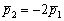 . Впрочем, можно и через коэффициенты самих уравнений:
. Впрочем, можно и через коэффициенты самих уравнений: 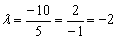 .
.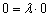
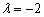 удовлетворяет данному уравнению (ему удовлетворяет вообще любое число).
удовлетворяет данному уравнению (ему удовлетворяет вообще любое число).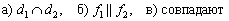 .
.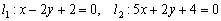
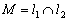 целесообразно искать аналитическим методом. Решим систему:
целесообразно искать аналитическим методом. Решим систему: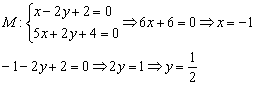
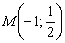
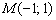 до прямой
до прямой 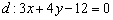
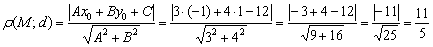
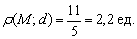
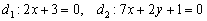 .
.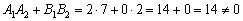 , значит, прямые не перпендикулярны.
, значит, прямые не перпендикулярны. 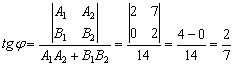
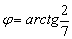
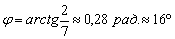
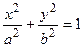
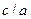 называется эксцентриситетом эллипса и обозначается:
называется эксцентриситетом эллипса и обозначается: 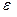 ,
, 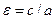 . Так как
. Так как 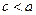 , то
, то 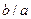 стремится к 1, т.е. b мало отличается от а и форма эллипса становится ближе к форме окружности. В предельном случае при
стремится к 1, т.е. b мало отличается от а и форма эллипса становится ближе к форме окружности. В предельном случае при 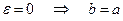 , получается окружность, уравнение которой есть
, получается окружность, уравнение которой есть


