Приходовский М.А.
Математика
Учебное пособие
Интегралы (до несобственного)
(осень 2019 - весна 2020, гр. 589-3, 129, 1В9).
ЛЕКЦИЯ 20. 3.12.2019
ГЛАВА 7. ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ.
Определения и основные методы.
Определение. Если 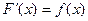 , то
, то 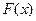 называется первообразной от функции
называется первообразной от функции  .
.
Свойство 1. Если 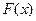 первообразная, то
первообразная, то  (для любого
(для любого 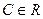 ) тоже является первообразной для той же самой функции
) тоже является первообразной для той же самой функции  .
.
Это легко доказать, действительно, 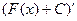 =
= 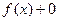 =
=  .
.
Таким образом, первообразных бесконечно много, то есть, если поднять или опустить на любую высоту график 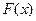 , снова будет первообразная.
, снова будет первообразная.
Свойство 2. Если 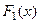 и
и 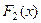 две различные первообразные функции
две различные первообразные функции  , то
, то  .
.
Доказывается так: 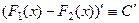 , т.е.
, т.е. 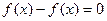 .
.
Определение. Множество всех первообразных от одной и той же функции  называется неопределённым интегралом этой функции. Обозначение:
называется неопределённым интегралом этой функции. Обозначение: 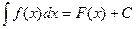 .
.
Свойства линейности.
1. 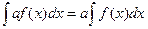 2.
2. 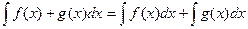
|
Замечание.
Для произведения аналогичное свойство  не верно. Чтобы убедиться в этом, достаточно рассмотреть любые 2 простейшие функции, например
не верно. Чтобы убедиться в этом, достаточно рассмотреть любые 2 простейшие функции, например  ,
, 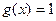 .
.
Тогда 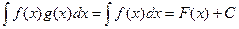 , в то же время:
, в то же время:
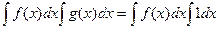 =
=  .
.
Таблица основных интегралов.
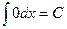
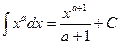 (
( )
)
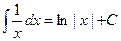
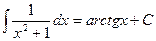
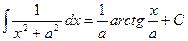
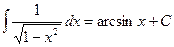
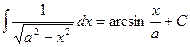

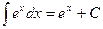
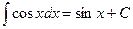 ;
; 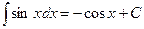


Объяснение причины возникновения модуля в 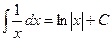 . Функция
. Функция 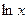 существует только на правой полуоси, тогда как
существует только на правой полуоси, тогда как 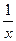 имеет две ветви, на правой и левой полуоси. Получалось бы противоречие, что производная от несуществующей функции есть на левой полуоси. Функция
имеет две ветви, на правой и левой полуоси. Получалось бы противоречие, что производная от несуществующей функции есть на левой полуоси. Функция 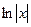 является чётным продолжением
является чётным продолжением 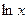 на левую полуось, и именно она там является первообразной для
на левую полуось, и именно она там является первообразной для 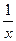 при
при 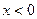 .
.
Методы интегрирования.
1. Преобразования подынтегральных выражений.
Различные преобразования, например, арифметические (домножить и поделить, прибавить и отнять), выделение полного квадрата, разбиение многочлена на множители, преобразования по тригонометрическим формулам, и т.д. нередко помогают упростить исходное выражение, разбить его на несколько более простых слагаемых, которые уже сводятся к интегралам табличного типа. На практике рассмотрены разнообразные примеры на виды этих преобразований. Часто нужно домножить и поделить, чтобы сформировать готовое выражение, являющееся производной от известной функции. Например,
Пример. 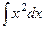 =
= 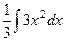 =
= 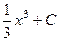 .
.
Когда сформировали выражение 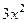 , а заодно поделили на 3 перед интегралом, теперь уже точно невозможно перепутать или забыть коэффициент.
, а заодно поделили на 3 перед интегралом, теперь уже точно невозможно перепутать или забыть коэффициент.
Аналогично, допустим, что мы помним, что  . Тогда можно постараться сформировать готовое выражение типа
. Тогда можно постараться сформировать готовое выражение типа 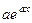 внутри интеграла. Тем самым мы автоматически докажем, что при интегрировании такое выражение на этот коэффициент делится, а не домножается:
внутри интеграла. Тем самым мы автоматически докажем, что при интегрировании такое выражение на этот коэффициент делится, а не домножается:
Пример.  =
= 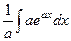 =
= 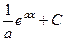 .
.
Тригонометрические преобразования:
Пример. Вычислить 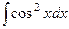 .
.
Решение. Применим формулу понижения степени.
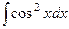 =
= 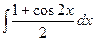 =
= 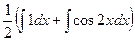 =
=
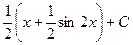 =
= 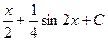 .
.
Пример. Вычислить  .
.
Решение.  =
=  =
= 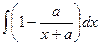 =
=
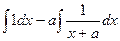 =
= 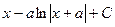 .
.
Ответ. 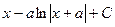 .
.
Замена переменной.
Бывают такие случаи, когда функция имеет вид  , то есть явно видно, что всё выражение зависит от какого-то однотипного блока, например всё выражается через
, то есть явно видно, что всё выражение зависит от какого-то однотипного блока, например всё выражается через 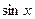 или
или  . Делается замена на
. Делается замена на 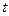 , только нужно не забыть пересчитать
, только нужно не забыть пересчитать 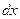 , потому что
, потому что 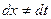 , если только замена не является простым линейным сдвигом
, если только замена не является простым линейным сдвигом 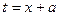 .
.
Пример. Вычислить  .
.
Решение. Сделаем замену 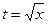 , тогда
, тогда 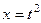 ,
,  ,
,  .
.
 =
=  =
= 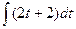 =
=  .
.
Обратная замена:  =
= 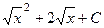 =
= 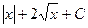 .
.
Более того, область определения исходной функции 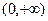 из-за наличия в ней квадратного корня, точка 0 не входит в область определения, так как корень там и в знаменателе, так что знак модуля в ответе является излишним, ответ можно записать так:
из-за наличия в ней квадратного корня, точка 0 не входит в область определения, так как корень там и в знаменателе, так что знак модуля в ответе является излишним, ответ можно записать так: 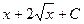 .
.
Если в функции присутствуют корни разного порядка, например  и
и 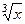 , то замена должна происходить через корень порядка НОК (наименьшее общее кратное). Причина в том, что именно при этом все корни переводятся в целые степени от
, то замена должна происходить через корень порядка НОК (наименьшее общее кратное). Причина в том, что именно при этом все корни переводятся в целые степени от 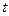 .
.
Если 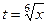 , тогда:
, тогда: 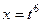 ,
, 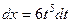 .
.
Объяснение, почему все корни выразятся через целые степени 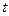 :
:
 =
= 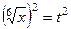 ,
,
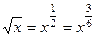 =
= 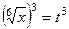 .
.
Интегрирование по частям.
Существует более общий метод, чем подведение под знак дифференциала. Иногда вовсе не требуется, чтобы первообразная от того множителя, который подводится под dx, была как-то связана с остальной частью функции. Запишите формулу:

Такой короткий вид легче выучить наизусть, а теперь запишем более подробно, чтобы понять смысл.
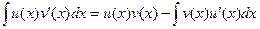 .
.
Если есть два множителя, и один из них интегрируется довольно легко (он обозначен  ) то можно перейти к интегралу, в котором наоборот,
) то можно перейти к интегралу, в котором наоборот, 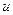 понижено до производной, а
понижено до производной, а  повышено до первообразной. Иногда именно это помогает упростить дальнейшие вычисления.
повышено до первообразной. Иногда именно это помогает упростить дальнейшие вычисления.
Доказательство формулы.
Вспомним, что по правилу дифференцирования произведения, которое мы доказывали в прошлом семестре: 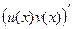 =
= 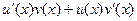 . Тогда
. Тогда  =
= 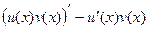 .
.
Тогда и неопределённые интегралы от этих двух функций совпадают:
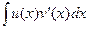 =
=  .
.
Но первообразная от производной, это сама функция и есть, т.е.
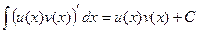 .
.
Поэтому 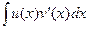 =
= 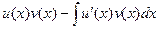 .
.
Пример. Вычислить 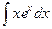 .
.
Решение. Если обозначить 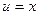 ,
, 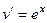 , то при переходе к
, то при переходе к  степенной понизится степень, в данном случае она вообще перейдёт в 1. А вот для второго множителя переходим к первообразной, но там не усложняется, остаётся точно так же как и было,
степенной понизится степень, в данном случае она вообще перейдёт в 1. А вот для второго множителя переходим к первообразной, но там не усложняется, остаётся точно так же как и было, 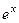 . Поэтому на следующем шаге интеграл содержит вообще не два множителя, а один!
. Поэтому на следующем шаге интеграл содержит вообще не два множителя, а один!
Составим таблицу:
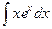 =
= 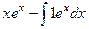 , тогда получаем ответ:
, тогда получаем ответ:  .
.
А есть такие случаи, когда функция состоит не из 2 множителей, а всего из одного, но мы ведь всё равно можем считать, что второй множитель есть, только он равен 1.
Пример. 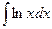 .
.
Здесь производная от подынтегральной функции устроена лучше и проще, чем сама функция, но правда, пришлось допустить некоторое незначительное усложнение типа функции при переходе от  к
к 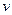 .
.
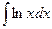 =
= 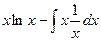 =
=  =
= 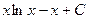 .
.
Интегралы вида 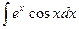 и
и 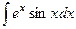 называются циклическими интегралами, потому что через 2 цикла вычисления «по частям» получается исходный интеграл в правой части выражения, т.е.
называются циклическими интегралами, потому что через 2 цикла вычисления «по частям» получается исходный интеграл в правой части выражения, т.е.  , откуда можно просто выразить
, откуда можно просто выразить  арифметическим путём.
арифметическим путём.
Вычислим интеграл 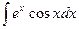 .
.
Пусть 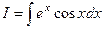 .
.
. На первом шаге, обозначаем  ,
,  .
.
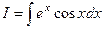 . =
. = 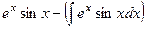 .
.
На 2-м шаге, в том интеграле, который получился, обозначим аналогичным образом:  ,
,  .
.
Получается 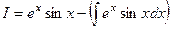 =
= 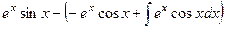 =
=  .
.
Из равенства 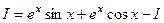 можно выразить
можно выразить 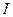 :
:
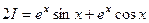 ,
, 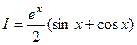 .
.
Ответ. 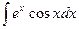 =
=  .
.
ЛЕКЦИЯ 21. 4.12.2019
Выведем формулу вычисления интегралов  . Обозначим всю функцию через u и применим интегрирование по частям, и при этом формально считаем второй множитель равным 1. Для удобства, временно применим отрицательные степени вместо дробей.
. Обозначим всю функцию через u и применим интегрирование по частям, и при этом формально считаем второй множитель равным 1. Для удобства, временно применим отрицательные степени вместо дробей.
 =
= 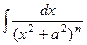 =
=  =
=
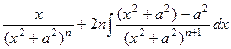
Теперь можем разбить на две дроби, интеграл от первой сводится к  , а второй к
, а второй к 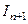 .
.
 =
= 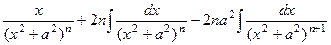 , то есть
, то есть
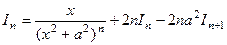 , откуда выразим
, откуда выразим 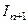 через
через  :
:
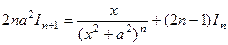 ,
,
вывели «рекурсивную» формулу 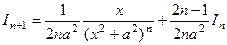 , с помощью которой интеграл такого типа для большей степени сводится к меньшей степени, а значит, все они последовательно сводятся к
, с помощью которой интеграл такого типа для большей степени сводится к меньшей степени, а значит, все они последовательно сводятся к  , который равен
, который равен 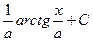 .
.
ЕКЦИЯ 22. 11.12.2019
ЛЕКЦИЯ 23. 17.12.2019
ЛЕКЦИЯ 24. 18.12.2019
Основной формулой в теме «определённый интеграл» является формула Ньютона-Лейбница 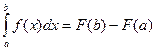 . Она позволяет сразу же вычислить определённый интеграл, если известен неопределённый.
. Она позволяет сразу же вычислить определённый интеграл, если известен неопределённый.
Но на самом деле, связь между этими двумя видами интегралов двусторонняя, т.е. и неопределённый интеграл может быть вычислен с помощью определённого. А именно, если рассматривать функцию 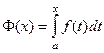 то есть определённый интеграл с переменным верхним пределом.
то есть определённый интеграл с переменным верхним пределом.
Теорема 1. Функция 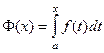 является первообразной от функции
является первообразной от функции 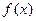 .
.
Доказательство. Нужно доказать, что  .
.
Рассмотрим подробнее производную функции 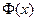 . По определению,
. По определению,
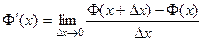 .
.
В данном случае, это  , по свойству 2, интеграл по отрезку
, по свойству 2, интеграл по отрезку 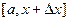 можно представить в виде суммы двух интегралов, а именно, по
можно представить в виде суммы двух интегралов, а именно, по 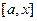 и
и 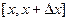 . Чертёж:
. Чертёж:
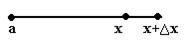
При этом интеграл по  там в разности есть ещё и со знаком «минус», то есть он в итоге сокращается.
там в разности есть ещё и со знаком «минус», то есть он в итоге сокращается.
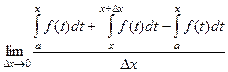 =
= 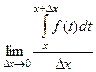 .
.
По свойству 10, интеграл по отрезку  можно представить как некоторое среднее значение, т.е. в какой-то точке
можно представить как некоторое среднее значение, т.е. в какой-то точке  , умноженное на длину отрезка.
, умноженное на длину отрезка.
В общем случае длина была равна 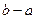 , а для данного отрезка это просто
, а для данного отрезка это просто 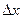 . Тогда:
. Тогда: 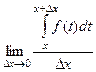 =
= 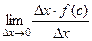 =
= 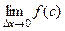 .
.
Однако точка 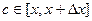 , поэтому при
, поэтому при  , точка
, точка 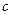 , которая находится где-то между
, которая находится где-то между  и
и  , стремится к левой границе отрезка:
, стремится к левой границе отрезка: 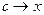 . Поэтому в итоге
. Поэтому в итоге 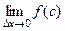 =
= 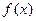 .
.
Теорема 2. (Ньютона-Лейбница). Если 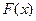 - какая-либо первообразная от
- какая-либо первообразная от 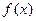 , то верна формула:
, то верна формула: 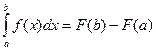 .
.
Доказательство. Если 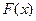 есть произвольная первообразная, то она отличается на какую-то константу
есть произвольная первообразная, то она отличается на какую-то константу 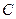 от той первообразной, которую мы рассматривали в теореме 1. То есть
от той первообразной, которую мы рассматривали в теореме 1. То есть 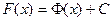 , что означает
, что означает
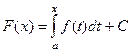 . Запишем это равенство в точке
. Запишем это равенство в точке 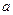 , получится
, получится 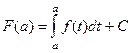 но ведь интеграл по одной точке это 0, там нулевая длина основания, а значит и нулевая площадь. Тогда
но ведь интеграл по одной точке это 0, там нулевая длина основания, а значит и нулевая площадь. Тогда 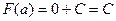 . вот, кстати, мы заодно и установили, как связана константа
. вот, кстати, мы заодно и установили, как связана константа 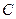 с выбором начальной точки
с выбором начальной точки 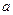 .
.
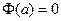 , а на сколько по высоте отличается от
, а на сколько по высоте отличается от 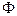 любая другая первообразная - это и есть значение
любая другая первообразная - это и есть значение  .
.
Итак, теперь ясно, что 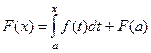 .
.
А теперь рассмотрим это выражение в точке  .
.
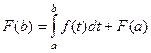 , то есть
, то есть  . Но ведь переменная
. Но ведь переменная 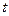 вводилась исключительно для того, чтобы отличать
вводилась исключительно для того, чтобы отличать  внутри функции и на верхнем пределе интеграла. Теперь, когда перешли к фиксированным границам в интеграле, можно сделать тривиальную замену
внутри функции и на верхнем пределе интеграла. Теперь, когда перешли к фиксированным границам в интеграле, можно сделать тривиальную замену 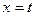 и запись примет вид
и запись примет вид 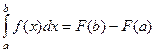 , что и требовалось доказать.
, что и требовалось доказать.
Примеры вычисления по формуле Ньютона-Лейбница.
Пример. Найти интегралы 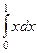 и
и 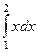 .
.
Решение. 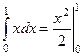 =
= 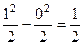 .
.
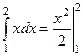 =
= 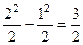 .
.
Пример. Найти 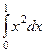 . Решение.
. Решение.  =
= 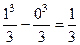 .
.
Пример. Найти интеграл  .
.
Решение.  . =
. = 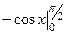 =
=  =
= 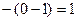 .
.
Пример. Найти интеграл  .
.
Решение.  =
= 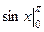 =
=  .
.
Замечание. Интеграл  , где
, где 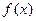 нечётная функция, равен 0, так как первообразная - чётная, и её значения при
нечётная функция, равен 0, так как первообразная - чётная, и её значения при  и
и  одинаковы, значит, по формуле Ньютона-Лейбница происходит полное вычитание,
одинаковы, значит, по формуле Ньютона-Лейбница происходит полное вычитание, 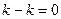 .
.
Вид формулы интегрирования по частям для определённого интеграла: 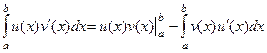 .
.
Особенности замены переменной в определённом интеграле (пересчёт пределов интегрирования, и можно не возвращаться к старой переменной, то есть не делать обратную замену).
Пример. Вычислить интеграл 
Решение.
1) Без замены.  =
= 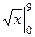 =
= 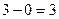 .
.
2) С помощью замены. При замене 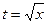 мы адаптируем границы к новой переменной, то есть, если
мы адаптируем границы к новой переменной, то есть, если  , то
, то 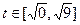 =
= 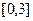 .
.
Тогда 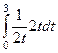 =
= 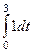 =
= 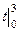 = 3.
= 3.
Конечно, старые границы могут остаться прежними, например, при такой замене 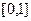 отобразится в
отобразится в 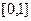 . Но, как правило, при замене верхний и нижний предел интегрирования тоже изменяются.
. Но, как правило, при замене верхний и нижний предел интегрирования тоже изменяются.
Замена в определённом интеграле должна задаваться взаимно-однозначной функцией 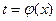 , то есть монотонной функцией. Иначе можно столкнуться с такими парадоксами: например,
, то есть монотонной функцией. Иначе можно столкнуться с такими парадоксами: например, 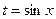 , интеграл от 0 до
, интеграл от 0 до 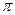 . Тогда по переменной
. Тогда по переменной 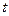 получаем интеграл по промежутку
получаем интеграл по промежутку 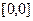 , и он был бы в любом случае равен 0. Чтобы избежать такого противоречия, надо было бы разбить исходный интеграл по переменной
, и он был бы в любом случае равен 0. Чтобы избежать такого противоречия, надо было бы разбить исходный интеграл по переменной 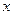 на 2 части, по
на 2 части, по 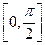 и
и 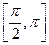 .
.
ЛЕКЦИЯ 25. 25.12.2019
Пункт 3. Вычисление длины дуги кривой.
Вывести формулу длины явно заданной кривой: 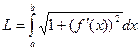 .
.
Доказательство (вывод формулы). Разобьём область определения на n частей, рассмотрим подробнее одну часть графика.
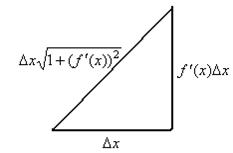
Длина фрагмента кривой приближённо равна гипотенузе. При этом, тангенс угла наклона равен производной. Поэтому, если горизонтальный катет 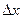 то вертикальный равен
то вертикальный равен  . Но в этом случае гипотенуза, по теореме Пифагора, равна:
. Но в этом случае гипотенуза, по теореме Пифагора, равна:
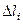 =
= 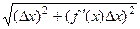 =
=  .
.
При переходе к пределу при 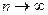 , получится
, получится 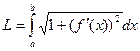 .
.
Чем круче наклон фрагмента графика, тем больше величина 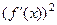 , и тем больше корень
, и тем больше корень 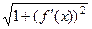 и соответственно, длина части этой кривой. Напротив, если график горизонтальный (функция = константа) то
и соответственно, длина части этой кривой. Напротив, если график горизонтальный (функция = константа) то 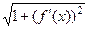 =
=  . Длина такой кривой просто равна длине отрезка в области определения, то есть
. Длина такой кривой просто равна длине отрезка в области определения, то есть 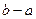 .
.
Для параметрически заданной в плоскости формула принимает такой вид: 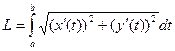 .
.
В трёхмерном пространстве: 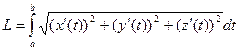 .
.
Пример. Вычислить длину участка кривой 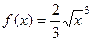 при
при 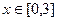 .
.
Решение. 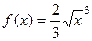 =
= 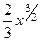
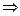
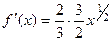 =
=  .
.
Тогда  =
= 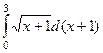 =
= 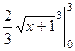 =
= 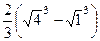 =
=
 =
= 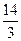 . Ответ.
. Ответ. 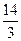 .
.
Полярная система координат. Кроме пары чисел 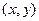 , которыми можно задать точку на плоскости, можно задать также и таким образом: соединим точку с началом координат, длину этого отрезка обозначим
, которыми можно задать точку на плоскости, можно задать также и таким образом: соединим точку с началом координат, длину этого отрезка обозначим 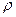 . Угол между осью
. Угол между осью  и этим отрезком обозначим
и этим отрезком обозначим 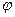 .
.
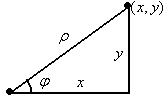
Так как  это прилежащий катет, а
это прилежащий катет, а  гипотенуза, тогда
гипотенуза, тогда 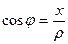 , аналогично
, аналогично  , откуда следуют такие формулы:
, откуда следуют такие формулы: 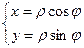
Например, для точки (1,1) полярные координаты: 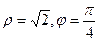 .
.
Некоторые кривые в полярных координатах задаются намного проще, чем в декартовых. Например, окружность радиуса 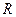 :
:  .
.
«Спираль Архимеда» 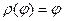 :
:
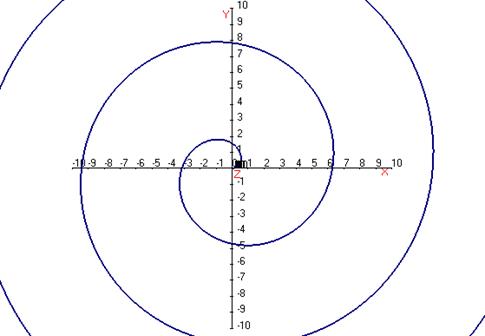
Впрочем, можно представлять в полярных координатах и прямые:
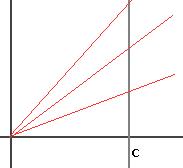
Пример. Построить уравнение прямой 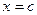 в полярных координатах.
в полярных координатах.
Решение. На чертеже видно, что чем больше угол наклона, тем больше расстояние. При  расстояние
расстояние  , при
, при  оно увеличивается до
оно увеличивается до 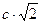 , а затем стремится к
, а затем стремится к 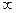 .
.
В уравнении  заменим
заменим  по формулам перехода к полярным координатам, т.е.
по формулам перехода к полярным координатам, т.е.  . Получается
. Получается 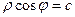 , тогда
, тогда 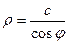 .
.
Ответ. 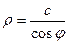 .
.
ПРАКТИКА
НЕОПРЕДЕЛЁННЫЙ ИНТЕГРАЛ
Элементарные преобразования
Задача 268. Вычислить 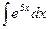 .
.
Решение. Известно, что  . При дифференцровании функций вида
. При дифференцровании функций вида  происходило умножение на константу, а при интегрировании наоборот, деление. Чтобы понять, почему это так, постараемся сначала сформировать внутри интеграла готовую производную от этой экспоненты, для чего домножим и поделим на 5.
происходило умножение на константу, а при интегрировании наоборот, деление. Чтобы понять, почему это так, постараемся сначала сформировать внутри интеграла готовую производную от этой экспоненты, для чего домножим и поделим на 5.
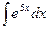 =
= 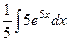 =
= 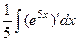 =
= 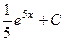 .
.
Ответ. 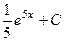 .
.
Задача 269. Вычислить 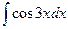 .
.
Решение. Замечая, что 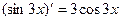 , преобразуем так:
, преобразуем так:
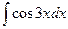 =
= 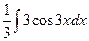 =
= 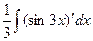 =
= 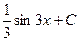 .
.
Ответ. 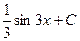 .
.
Задача 270. Вычислить 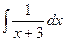 .
.
Решение. Известна формула 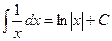 . Если в знаменателе линейная функция вида
. Если в знаменателе линейная функция вида 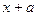 , то можно добавить константу под знаком дифференциала, от этого ничего не изменилось бы, ведь производная константы это 0. Итак,
, то можно добавить константу под знаком дифференциала, от этого ничего не изменилось бы, ведь производная константы это 0. Итак, 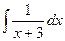 =
= 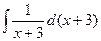 . Теперь интеграл имеет вид
. Теперь интеграл имеет вид 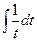 и конечно, равен
и конечно, равен  . Фактически применили замену
. Фактически применили замену 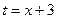 . Сделав обратную замену, получаем ответ:
. Сделав обратную замену, получаем ответ: 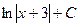 .
.
Ответ. 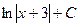 .
.
Задача 271. Вычислить 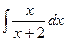 .
.
Решение. Здесь, в отличие от прошлой задачи, уже и в числителе есть переменная, то есть здесь неправильная дробь. Сначала нужно выделить целую часть дроби и отделить правильную дробь. В данном случае для этого достаточно прибавить и отнять 2 в числителе.
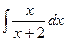 =
= 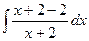 =
= 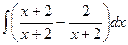 =
= 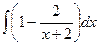 =
=
= 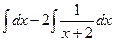 и теперь, когда разбили на сумму или разность табличных интегралов, получаем ответ:
и теперь, когда разбили на сумму или разность табличных интегралов, получаем ответ:  .
.
Ответ. 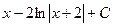 .
.
Задача 272. Вычислить 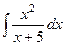 .
.
Решение. В данном случае неправильная дробь, причём степень в числителе более высокая. Можно применить общий метод выделения целой части, то есть поделить числитель на знаменатель.

Получили частное 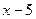 , остаток
, остаток 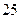 . Теперь можно представить в виде суммы интегралов:
. Теперь можно представить в виде суммы интегралов:
 =
=  =
=  .
.
Впрочем, можно и не делить столбиком, а просто отнять и прибавить 25, тогда  =
= 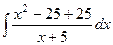 =
= 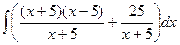 что тоже приводит к
что тоже приводит к 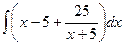 .
.
Теперь, когда свели к сумме табличных интегралов, то с помощью уже ранее изученных действий получаем ответ:
Ответ. 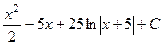 .
.
Задача 273. Вычислить  .
.
Решение. Дискриминант знаменателя отрицательный, поэтому здесь невозможно сделать как в прошлой задаче, так как нет корней знаменателя и дробь невозможно свести к виду 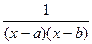 .
.
Но при D < 0 можно выделить полный квадрат:
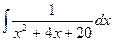 =
= 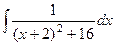 =
= 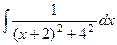 .
.
С помощью замены 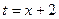 сводится к интегралу:
сводится к интегралу:
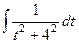 =
= 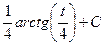 , и далее с помощью обратной замены получаем ответ.
, и далее с помощью обратной замены получаем ответ.
Ответ. 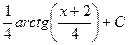 .
.
Задача 274. Вычислить 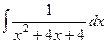 .
.
Решение. В предыдущей задаче было D<0, а в этой D=0.
Выделяя полный квадрат, получим 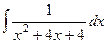 =
=  .
.
В этом случае сводится не к арктангенсу, а к степенной функции, потому что получается 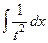 =
=  =
= 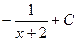 .
.
Ответ. 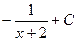 .
.
Задача 275. Доказать формулу 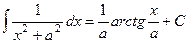 .
.
Решение. Известно, что 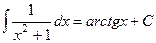 .
.
В выражении 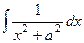 Вынесем за скобку
Вынесем за скобку 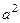 в знаменателе.
в знаменателе.
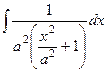 =
= 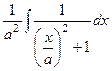 , далее цель - получить
, далее цель - получить  везде, в том числе и под знаком дифференциала, чтобы сделать замену
везде, в том числе и под знаком дифференциала, чтобы сделать замену 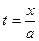 . Домножим и поделим на
. Домножим и поделим на 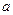 :
:
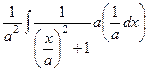 =
=  =
=  =
=
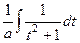 =
= 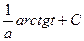 =
=  .
.
Задача 276. Вычислить 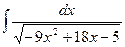 .
.
Решение. 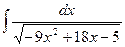 =
= 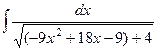 =
=  =
= 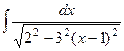 =
= 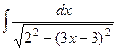 .
.
Для того, чтобы применить формулу, 
нужно обозначить 
|
|
|



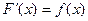 , то
, то 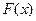 называется первообразной от функции
называется первообразной от функции  .
. (для любого
(для любого 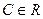 ) тоже является первообразной для той же самой функции
) тоже является первообразной для той же самой функции 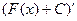 =
= 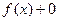 =
= 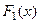 и
и 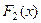 две различные первообразные функции
две различные первообразные функции  .
.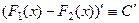 , т.е.
, т.е. 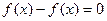 .
.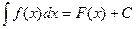 .
.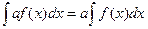 2.
2. 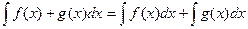
 не верно. Чтобы убедиться в этом, достаточно рассмотреть любые 2 простейшие функции, например
не верно. Чтобы убедиться в этом, достаточно рассмотреть любые 2 простейшие функции, например  ,
, 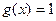 .
.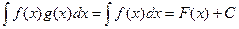 , в то же время:
, в то же время: 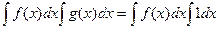 =
=  .
.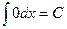
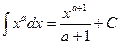 (
( )
)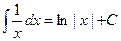
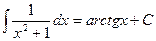
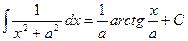
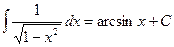
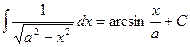

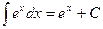
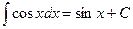 ;
; 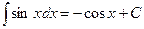


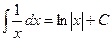 . Функция
. Функция 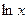 существует только на правой полуоси, тогда как
существует только на правой полуоси, тогда как 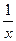 имеет две ветви, на правой и левой полуоси. Получалось бы противоречие, что производная от несуществующей функции есть на левой полуоси. Функция
имеет две ветви, на правой и левой полуоси. Получалось бы противоречие, что производная от несуществующей функции есть на левой полуоси. Функция 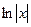 является чётным продолжением
является чётным продолжением 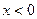 .
.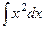 =
= 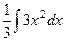 =
= 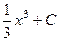 .
.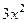 , а заодно поделили на 3 перед интегралом, теперь уже точно невозможно перепутать или забыть коэффициент.
, а заодно поделили на 3 перед интегралом, теперь уже точно невозможно перепутать или забыть коэффициент. . Тогда можно постараться сформировать готовое выражение типа
. Тогда можно постараться сформировать готовое выражение типа 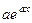 внутри интеграла. Тем самым мы автоматически докажем, что при интегрировании такое выражение на этот коэффициент делится, а не домножается:
внутри интеграла. Тем самым мы автоматически докажем, что при интегрировании такое выражение на этот коэффициент делится, а не домножается:  =
= 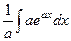 =
= 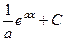 .
.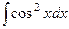 .
.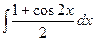 =
= 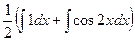 =
=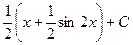 =
= 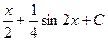 .
. .
.  =
= 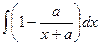 =
=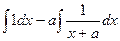 =
= 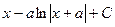 .
. , то есть явно видно, что всё выражение зависит от какого-то однотипного блока, например всё выражается через
, то есть явно видно, что всё выражение зависит от какого-то однотипного блока, например всё выражается через  или
или  . Делается замена на
. Делается замена на 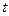 , только нужно не забыть пересчитать
, только нужно не забыть пересчитать 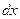 , потому что
, потому что 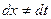 , если только замена не является простым линейным сдвигом
, если только замена не является простым линейным сдвигом 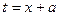 .
. .
.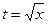 , тогда
, тогда 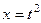 ,
,  ,
,  .
. =
= 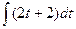 =
=  .
.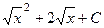 =
= 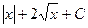 .
. из-за наличия в ней квадратного корня, точка 0 не входит в область определения, так как корень там и в знаменателе, так что знак модуля в ответе является излишним, ответ можно записать так:
из-за наличия в ней квадратного корня, точка 0 не входит в область определения, так как корень там и в знаменателе, так что знак модуля в ответе является излишним, ответ можно записать так: 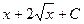 .
.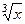 , то замена должна происходить через корень порядка НОК (наименьшее общее кратное). Причина в том, что именно при этом все корни переводятся в целые степени от
, то замена должна происходить через корень порядка НОК (наименьшее общее кратное). Причина в том, что именно при этом все корни переводятся в целые степени от 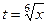 , тогда:
, тогда: 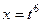 ,
, 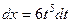 .
. =
= 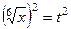 ,
,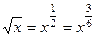 =
= 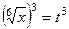 .
.
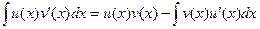 .
. ) то можно перейти к интегралу, в котором наоборот,
) то можно перейти к интегралу, в котором наоборот, 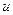 понижено до производной, а
понижено до производной, а 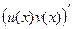 =
= 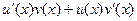 . Тогда
. Тогда  =
= 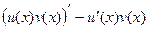 .
.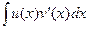 =
=  .
.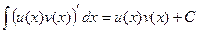 .
.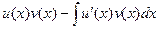 .
.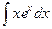 .
. 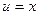 ,
, 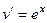 , то при переходе к
, то при переходе к  степенной понизится степень, в данном случае она вообще перейдёт в 1. А вот для второго множителя переходим к первообразной, но там не усложняется, остаётся точно так же как и было,
степенной понизится степень, в данном случае она вообще перейдёт в 1. А вот для второго множителя переходим к первообразной, но там не усложняется, остаётся точно так же как и было, 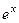 . Поэтому на следующем шаге интеграл содержит вообще не два множителя, а один!
. Поэтому на следующем шаге интеграл содержит вообще не два множителя, а один!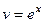
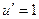
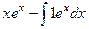 , тогда получаем ответ:
, тогда получаем ответ:  .
.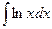 .
.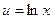
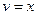
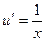
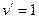
 .
.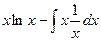 =
=  =
= 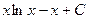 .
.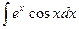 и
и 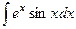 называются циклическими интегралами, потому что через 2 цикла вычисления «по частям» получается исходный интеграл в правой части выражения, т.е.
называются циклическими интегралами, потому что через 2 цикла вычисления «по частям» получается исходный интеграл в правой части выражения, т.е.  , откуда можно просто выразить
, откуда можно просто выразить  арифметическим путём.
арифметическим путём.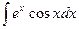 .
.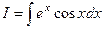 .
. ,
,  .
.
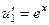
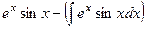 .
. ,
,  .
.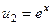


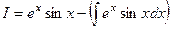 =
= 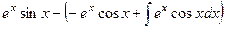 =
=  .
.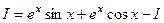 можно выразить
можно выразить 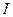 :
: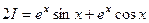 ,
, 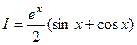 .
. .
. . Обозначим всю функцию через u и применим интегрирование по частям, и при этом формально считаем второй множитель равным 1. Для удобства, временно применим отрицательные степени вместо дробей.
. Обозначим всю функцию через u и применим интегрирование по частям, и при этом формально считаем второй множитель равным 1. Для удобства, временно применим отрицательные степени вместо дробей.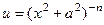

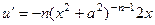
 =
= 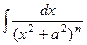 =
=  =
=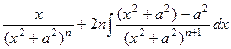
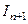 .
.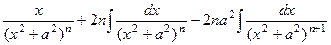 , то есть
, то есть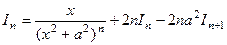 , откуда выразим
, откуда выразим 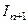 через
через 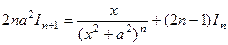 ,
,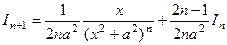 , с помощью которой интеграл такого типа для большей степени сводится к меньшей степени, а значит, все они последовательно сводятся к
, с помощью которой интеграл такого типа для большей степени сводится к меньшей степени, а значит, все они последовательно сводятся к  , который равен
, который равен 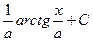 .
.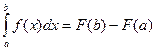 . Она позволяет сразу же вычислить определённый интеграл, если известен неопределённый.
. Она позволяет сразу же вычислить определённый интеграл, если известен неопределённый.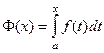 то есть определённый интеграл с переменным верхним пределом.
то есть определённый интеграл с переменным верхним пределом.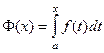 является первообразной от функции
является первообразной от функции 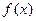 .
.  .
.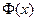 . По определению,
. По определению,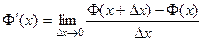 .
. , по свойству 2, интеграл по отрезку
, по свойству 2, интеграл по отрезку 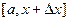 можно представить в виде суммы двух интегралов, а именно, по
можно представить в виде суммы двух интегралов, а именно, по 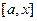 и
и 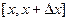 . Чертёж:
. Чертёж:
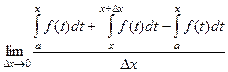 =
= 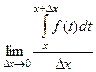 .
. можно представить как некоторое среднее значение, т.е. в какой-то точке
можно представить как некоторое среднее значение, т.е. в какой-то точке  , умноженное на длину отрезка.
, умноженное на длину отрезка.
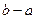 , а для данного отрезка это просто
, а для данного отрезка это просто 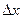 . Тогда:
. Тогда: 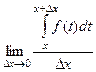 =
= 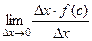 =
= 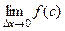 .
.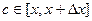 , поэтому при
, поэтому при  , точка
, точка 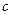 , которая находится где-то между
, которая находится где-то между  и
и  , стремится к левой границе отрезка:
, стремится к левой границе отрезка: 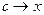 . Поэтому в итоге
. Поэтому в итоге 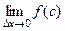 =
= 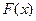 - какая-либо первообразная от
- какая-либо первообразная от 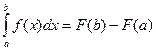 .
. 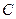 от той первообразной, которую мы рассматривали в теореме 1. То есть
от той первообразной, которую мы рассматривали в теореме 1. То есть 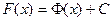 , что означает
, что означает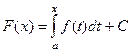 . Запишем это равенство в точке
. Запишем это равенство в точке 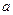 , получится
, получится 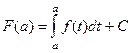 но ведь интеграл по одной точке это 0, там нулевая длина основания, а значит и нулевая площадь. Тогда
но ведь интеграл по одной точке это 0, там нулевая длина основания, а значит и нулевая площадь. Тогда 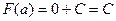 . вот, кстати, мы заодно и установили, как связана константа
. вот, кстати, мы заодно и установили, как связана константа 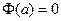 , а на сколько по высоте отличается от
, а на сколько по высоте отличается от 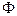 любая другая первообразная - это и есть значение
любая другая первообразная - это и есть значение  .
. .
. .
.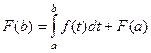 , то есть
, то есть  . Но ведь переменная
. Но ведь переменная 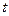 вводилась исключительно для того, чтобы отличать
вводилась исключительно для того, чтобы отличать 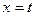 и запись примет вид
и запись примет вид 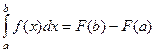 , что и требовалось доказать.
, что и требовалось доказать.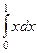 и
и 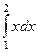 .
.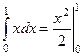 =
= 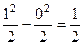 .
.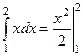 =
= 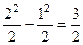 .
.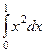 . Решение.
. Решение.  =
= 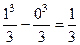 .
. .
.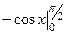 =
=  =
= 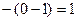 .
. .
.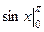 =
=  .
. , где
, где  и
и  одинаковы, значит, по формуле Ньютона-Лейбница происходит полное вычитание,
одинаковы, значит, по формуле Ньютона-Лейбница происходит полное вычитание, 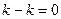 .
.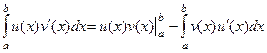 .
.
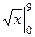 =
= 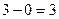 .
.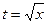 мы адаптируем границы к новой переменной, то есть, если
мы адаптируем границы к новой переменной, то есть, если  , то
, то 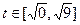 =
= 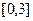 .
.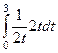 =
= 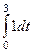 =
= 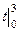 = 3.
= 3.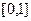 отобразится в
отобразится в 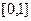 . Но, как правило, при замене верхний и нижний предел интегрирования тоже изменяются.
. Но, как правило, при замене верхний и нижний предел интегрирования тоже изменяются.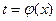 , то есть монотонной функцией. Иначе можно столкнуться с такими парадоксами: например,
, то есть монотонной функцией. Иначе можно столкнуться с такими парадоксами: например, 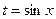 , интеграл от 0 до
, интеграл от 0 до 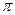 . Тогда по переменной
. Тогда по переменной 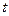 получаем интеграл по промежутку
получаем интеграл по промежутку 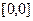 , и он был бы в любом случае равен 0. Чтобы избежать такого противоречия, надо было бы разбить исходный интеграл по переменной
, и он был бы в любом случае равен 0. Чтобы избежать такого противоречия, надо было бы разбить исходный интеграл по переменной 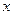 на 2 части, по
на 2 части, по 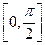 и
и 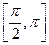 .
.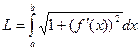 .
.
 . Но в этом случае гипотенуза, по теореме Пифагора, равна:
. Но в этом случае гипотенуза, по теореме Пифагора, равна: 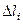 =
= 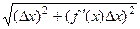 =
=  .
. , получится
, получится 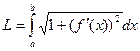 .
.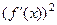 , и тем больше корень
, и тем больше корень 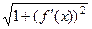 и соответственно, длина части этой кривой. Напротив, если график горизонтальный (функция = константа) то
и соответственно, длина части этой кривой. Напротив, если график горизонтальный (функция = константа) то 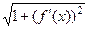 =
=  . Длина такой кривой просто равна длине отрезка в области определения, то есть
. Длина такой кривой просто равна длине отрезка в области определения, то есть 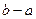 .
.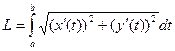 .
.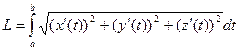 .
.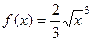 при
при 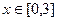 .
.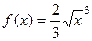 =
= 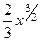
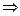
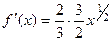 =
=  .
.  =
= 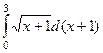 =
= 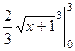 =
= 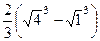 =
= =
= 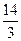 . Ответ.
. Ответ. 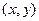 , которыми можно задать точку на плоскости, можно задать также и таким образом: соединим точку с началом координат, длину этого отрезка обозначим
, которыми можно задать точку на плоскости, можно задать также и таким образом: соединим точку с началом координат, длину этого отрезка обозначим 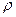 . Угол между осью
. Угол между осью 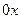 и этим отрезком обозначим
и этим отрезком обозначим 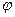 .
.
 это прилежащий катет, а
это прилежащий катет, а 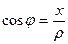 , аналогично
, аналогично  , откуда следуют такие формулы:
, откуда следуют такие формулы: 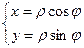
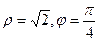 .
.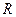 :
:  .
. 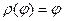 :
: 
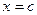 в полярных координатах.
в полярных координатах. расстояние
расстояние  , при
, при  оно увеличивается до
оно увеличивается до 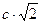 , а затем стремится к
, а затем стремится к 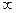 .
.
 заменим
заменим  по формулам перехода к полярным координатам, т.е.
по формулам перехода к полярным координатам, т.е.  . Получается
. Получается 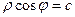 , тогда
, тогда 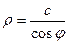 .
.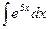 .
. . При дифференцровании функций вида
. При дифференцровании функций вида  происходило умножение на константу, а при интегрировании наоборот, деление. Чтобы понять, почему это так, постараемся сначала сформировать внутри интеграла готовую производную от этой экспоненты, для чего домножим и поделим на 5.
происходило умножение на константу, а при интегрировании наоборот, деление. Чтобы понять, почему это так, постараемся сначала сформировать внутри интеграла готовую производную от этой экспоненты, для чего домножим и поделим на 5.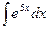 =
= 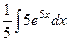 =
= 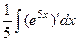 =
= 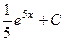 .
. 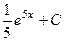 .
.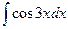 .
.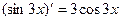 , преобразуем так:
, преобразуем так: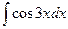 =
= 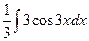 =
= 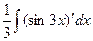 =
= 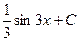 .
.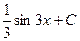 .
.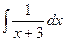 .
. 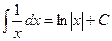 . Если в знаменателе линейная функция вида
. Если в знаменателе линейная функция вида 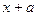 , то можно добавить константу под знаком дифференциала, от этого ничего не изменилось бы, ведь производная константы это 0. Итак,
, то можно добавить константу под знаком дифференциала, от этого ничего не изменилось бы, ведь производная константы это 0. Итак, 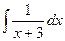 =
= 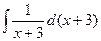 . Теперь интеграл имеет вид
. Теперь интеграл имеет вид 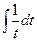 и конечно, равен
и конечно, равен  . Фактически применили замену
. Фактически применили замену 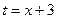 . Сделав обратную замену, получаем ответ:
. Сделав обратную замену, получаем ответ: 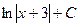 .
.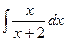 .
. 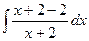 =
= 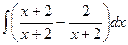 =
= 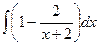 =
=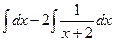 и теперь, когда разбили на сумму или разность табличных интегралов, получаем ответ:
и теперь, когда разбили на сумму или разность табличных интегралов, получаем ответ:  .
.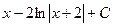 .
.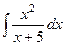 .
.
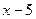 , остаток
, остаток 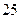 . Теперь можно представить в виде суммы интегралов:
. Теперь можно представить в виде суммы интегралов: =
=  =
=  .
.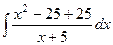 =
= 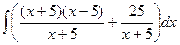 что тоже приводит к
что тоже приводит к 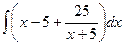 .
.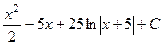 .
. .
.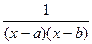 .
.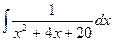 =
= 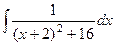 =
= 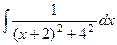 .
.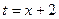 сводится к интегралу:
сводится к интегралу: 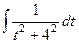 =
= 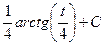 , и далее с помощью обратной замены получаем ответ.
, и далее с помощью обратной замены получаем ответ.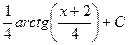 .
.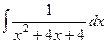 .
.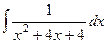 =
=  .
.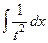 =
=  =
= 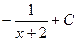 .
.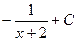 .
.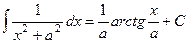 .
. 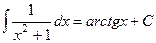 .
.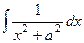 Вынесем за скобку
Вынесем за скобку 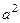 в знаменателе.
в знаменателе.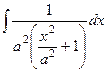 =
= 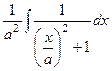 , далее цель - получить
, далее цель - получить  везде, в том числе и под знаком дифференциала, чтобы сделать замену
везде, в том числе и под знаком дифференциала, чтобы сделать замену 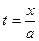 . Домножим и поделим на
. Домножим и поделим на 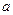 :
: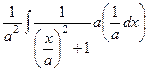 =
=  =
=  =
=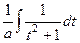 =
= 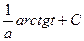 =
=  .
.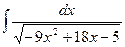 .
.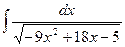 =
= 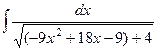 =
=  =
= 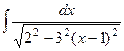 =
= 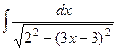 .
.