

Кормораздатчик мобильный электрифицированный: схема и процесс работы устройства...

Историки об Елизавете Петровне: Елизавета попала между двумя встречными культурными течениями, воспитывалась среди новых европейских веяний и преданий...

Кормораздатчик мобильный электрифицированный: схема и процесс работы устройства...

Историки об Елизавете Петровне: Елизавета попала между двумя встречными культурными течениями, воспитывалась среди новых европейских веяний и преданий...
Топ:
Отражение на счетах бухгалтерского учета процесса приобретения: Процесс заготовления представляет систему экономических событий, включающих приобретение организацией у поставщиков сырья...
Установка замедленного коксования: Чем выше температура и ниже давление, тем место разрыва углеродной цепи всё больше смещается к её концу и значительно возрастает...
Эволюция кровеносной системы позвоночных животных: Биологическая эволюция – необратимый процесс исторического развития живой природы...
Интересное:
Средства для ингаляционного наркоза: Наркоз наступает в результате вдыхания (ингаляции) средств, которое осуществляют или с помощью маски...
Финансовый рынок и его значение в управлении денежными потоками на современном этапе: любому предприятию для расширения производства и увеличения прибыли нужны...
Принципы управления денежными потоками: одним из методов контроля за состоянием денежной наличности является...
Дисциплины:
|
из
5.00
|
Заказать работу |
Задача 312. Вычислить интеграл 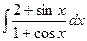 .
.
Решение. Функция не обладает свойствами чётности или нечётности, то есть, сменив знак синуса или косинуса, мы не получим, что знак минус будет у всей дроби. Поэтому применяем универсальную тригонометрическую подстановку:  . Напомним, что при этом
. Напомним, что при этом
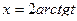 ,
, 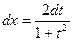 ,
,  ,
, 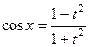 .
.
Итак, сделаем замену:
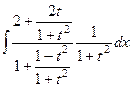 =
=  =
= 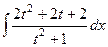 =
=
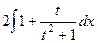 =
= 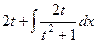 =
= 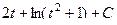 .
.
Теперь сделаем обратную замену. 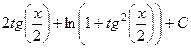 , что ещё можно привести к виду
, что ещё можно привести к виду 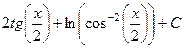 .
.
Ответ. 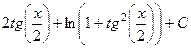 .
.
Примеры на другие подстановки.
Задача 313. Вычислить интеграл 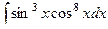 .
.
Решение. Здесь нечётная степень синуса, применяем замену  . Тогда
. Тогда 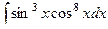 =
=  =
= 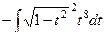 =
=
 =
= 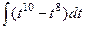 =
= 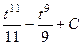 =
= 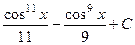 .
.
Ответ. 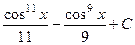 .
.
Замечание. Универсальная подстановка здесь приводит к огромным вычислениям. Попробуем применить её:
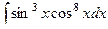 =
= 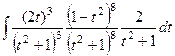 =
= 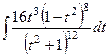 .
.
Если раскрыть скобки в числителе, и разбить на сумму множества дробей, то в знаменателе будут степени от 1 до 12, т.е. до 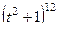 , то есть каждое слагаемое надо будет вычислять по рекуррентной формуле, последнее в 12 шагов. Но до того, надо было бы разложить на простейшие дроби, для чего решить систему с 24 неизвестными.
, то есть каждое слагаемое надо будет вычислять по рекуррентной формуле, последнее в 12 шагов. Но до того, надо было бы разложить на простейшие дроби, для чего решить систему с 24 неизвестными.
Задача 314. Вычислить интеграл 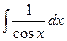 .
.
Решение. Сделаем замену 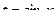 .
.
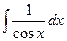 =
=  =
= 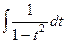 вот и свелось к рациональной дроби, и дальше для t можем действовать в рамках прошлой темы «рациональные дроби».
вот и свелось к рациональной дроби, и дальше для t можем действовать в рамках прошлой темы «рациональные дроби».
 =
= 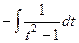 =
=  =
= 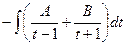 . Приводим к общему знаменателю:
. Приводим к общему знаменателю:
 =
= 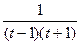 , далее
, далее  ,
,
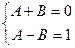 , отсюда следует
, отсюда следует 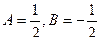 .
.
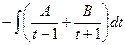 =
= 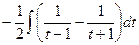 =
= 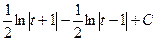
это можно после обратной замены и применения свойств логарифмов, записать так: 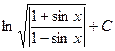 .
.
Ответ. 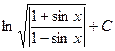 .
.
Задача 315. Вычислить интеграл 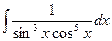 .
.
Решение.
Допустим, что мы воспользовались бы заменой 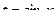 , заметив, что степень синуса нечётная. Тогда получалось бы:
, заметив, что степень синуса нечётная. Тогда получалось бы:
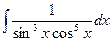 =
= 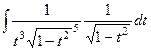 =
= 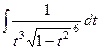 =
= 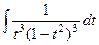 . Но при разложениии на простейшие дроби
. Но при разложениии на простейшие дроби
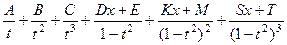
мы сталкивались бы с системой из 9 неизвестных. Поэтому, заметив, что суммарная степень чётная, сделаем замену 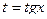 (3-й случай, в см. лекциях). Эта замена действительно окажется более рациональна в данном случае.
(3-й случай, в см. лекциях). Эта замена действительно окажется более рациональна в данном случае.
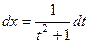 .
. 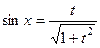 ,
, 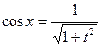 .
.
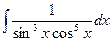 =
=  =
=  =
=
 =
= 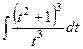 =
= 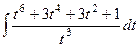
здесь мы воспользовались формулой 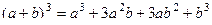 .
.
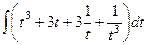 =
= 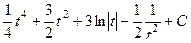 .
.
После обратной замены получаем ответ:
Ответ. 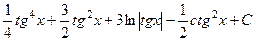 .
.
Задача 316. Вычислить интеграл  .
.
Решение. Здесь суммарная степень чётная, то есть, если сменить знак перед sin и cos, то знак сменится 2 раза, и останется «+». Поэтому надо применить замену 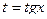 . Тогда (см. в лекции):
. Тогда (см. в лекции):
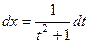 .
. 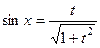 ,
, 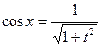 .
.
 =
= 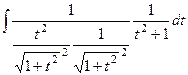 =
= 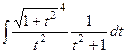 =
= 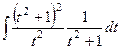 =
= 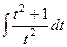 =
= 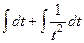 =
= 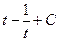 .
.
После обратной замены получается:  .
.
Ответ. 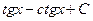 .
.
Проверка. 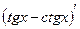 =
=  =
= 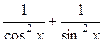 =
=
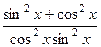 =
= 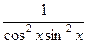 .
.
Задача 317. Вычислить интеграл 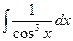 .
.
Решение. Функция нечётная относительно косинуса, замена 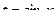 .
.
Тогда  ,
, 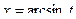 ,
, 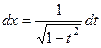 .
.
Однако в этом примере квадратные корни не сокращаются, а наоборот, умножаются, ведь косинус теперь не в числителе, а в знаменателе: 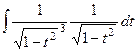 .
.
Но всё равно, будет чётная степень корня: 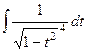 .
.
Итак, 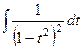 , что равно
, что равно  =
=  .
.
Теперь мы можем воспользоваться тем разложением, которое получали для такого случая в теме «рациональные дроби» на прошлой практике, где оба корня знаменателя кратные (см. задачу 305).
Курс специально построен так, чтобы использовать некоторые коэффициенты из старых примеров и не искать их здесь повторно.
Разложение было такое: 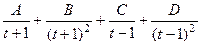 .
.
После приведения к общему знаменателю и решения системы уравнений, там получалось 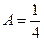 ,
, 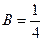 ,
, 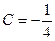 ,
, 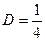 .
.
Итак,  =
= 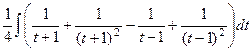 =
=
=  =
=
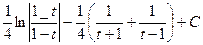 =
= 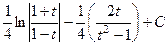 .
.
Сделаем обратную замену. 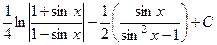 .
.
Ответ. 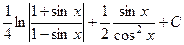 .
.
Задача 318. Вычислить интеграл 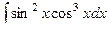 .
.
Решение. Функция нечётна относительно косинуса, значит, замена 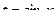 . Тогда
. Тогда
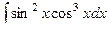 =
=  =
=  =
= 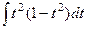 =
= 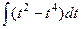 =
= 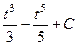 , после обратной замены получаем
, после обратной замены получаем 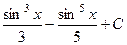 .
.
Ответ. 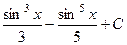
Задача 319. Вычислить интеграл  .
.
Решение. Аналогично прошлой задаче, 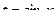 , тогда
, тогда
 =
= 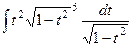 =
=  =
=  =
= 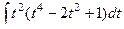 =
= 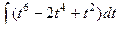 =
= 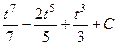 , после обратной замены
, после обратной замены 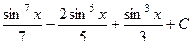 .
.
Ответ. 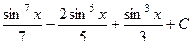
Задача 320. Вычислить интеграл 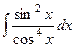 .
.
Решение. Суммарная степень чётна, поэтому применяется замена
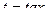 , тогда
, тогда 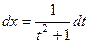 ,
, 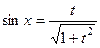 ,
, 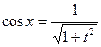 .
.
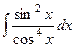 =
=  =
= 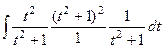 =
=
= 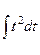 =
=  =
= 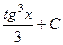 после обратной замены.
после обратной замены.
Ответ. 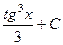
А сейчас мы увидим, как данная замена позволяет с лёгкостью доказать одну из формул из таблицы интегралов, а именно,
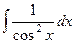 =
= 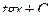 .
.
Задача 321. Вычислить интеграл 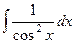 .
.
Решение. 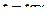 , тогда
, тогда 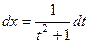 ,
, 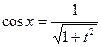 .
.
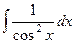 =
=  =
= 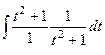 =
= 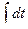 =
=  =
= 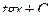 . Ответ.
. Ответ. 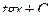 .
.
Взаимосвязь иррациональностей и тригонометрических функций. Примеры с интегралами, содержащими  , решаемые с помощью тригонометрических функций.
, решаемые с помощью тригонометрических функций.
Задача 322. Вычислить интеграл  .
.
Решение. В интеграле 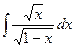 обозначим
обозначим  , при этом
, при этом 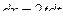 . При этом, правда, второй корень усложняется:
. При этом, правда, второй корень усложняется:
 =
= 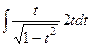 =
=  .
.
Необходима 2-я замена, чтобы устранить корень 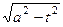 .
.
У нас здесь 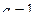 . Вводим замену
. Вводим замену 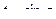 . Тогда
. Тогда 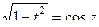 .
.
Итак,  =
= 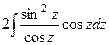 =
= 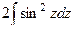 .
.
Теперь уже просто по формуле понижения степени.
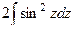 =
= 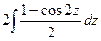 =
= 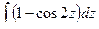 =
= 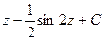 =
=
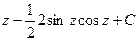 =
=  .
.
Обратные замены: сначала обращаем обратно вторую замену, которыу сделали последней: если 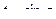 то
то 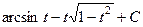 .
.
Далее, обращаем 1-ю замену:  , тогда в итоге:
, тогда в итоге:
Ответ. 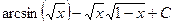 .
.
Задача 323. Вычислить интеграл 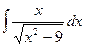 .
.
Решение. В этом случае нужно замена (см. лекции) 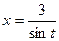 .
.
При этом корень квадратный исчезает таким образом:
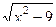 =
= 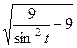 =
= 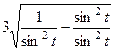 =
= 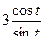 .
.
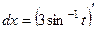 =
= 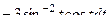 =
= 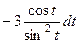 .
.
Итак, 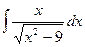 =
=  =
=
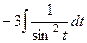 =
= 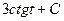 .
.
Для обратной замены, вспомним, что 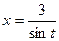 , то есть
, то есть 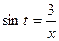 ,
, 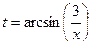 . Тогда
. Тогда 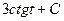 =
= 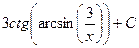 . Получается, что надо найти котангенс того угла, синус которого равен
. Получается, что надо найти котангенс того угла, синус которого равен 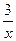 . Подпишем соответствующие стороны на чертеже прямоугольного треугольника.
. Подпишем соответствующие стороны на чертеже прямоугольного треугольника.
Третья сторона вычисляется по теореме Пифагора: 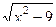 .
.
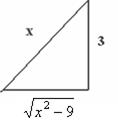
Котангенс этого угла: 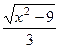 .
.
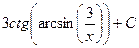 =
= 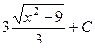 =
= 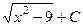 .
.
Ответ. 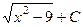 .
.
Определённый интеграл
Задача 324. Вычислить 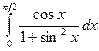
Решение.  =
= 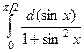
здесь мы можем заменить 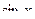 на
на 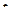 , но тогда нужно сделать пересчёт верхнего и нижнего пределов. Если
, но тогда нужно сделать пересчёт верхнего и нижнего пределов. Если 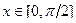 то
то 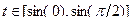 , т.е.
, т.е. 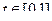 .
.
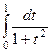 =
= 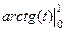 =
= 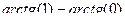 =
= 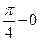 =
= 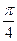 .
.
А можно было сначала вычислять интеграл как неопределённый, тогда надо было бы вернуться к исходной переменной 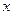 (то есть сделать обратную замену), но пределы можно не пересчитывать.
(то есть сделать обратную замену), но пределы можно не пересчитывать.
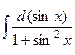 =
= 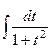 =
= 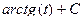 =
= 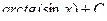
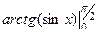 =
=  =
= 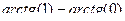 =
= 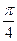 .
.
Впрочем, как видно, от способа не зависит, получается один и тот же ответ 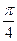 .
.
Задача 325. Вычислить интеграл 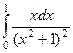 .
.
Решение. 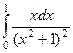 =
=  =
= 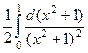 сделаем замену
сделаем замену 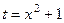 , при которой, если
, при которой, если 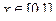 , то
, то 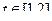 . Тогда:
. Тогда:
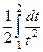 =
= 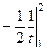 =
=  =
= 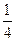 . Ответ.
. Ответ. 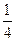 .
.
СЕМЕСТР 2
Определённый интеграл
Задача 1. Вычислить интеграл 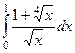 .
.
При этом осуществляется повторение темы «интегрирование иррациональностей».
Решение. НОК(2,4) = 4, поэтому замена 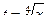 . При такой замене
. При такой замене  ,
, 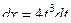 ,
, 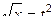 .
. 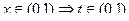 .
.
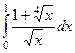 =
= 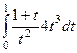 =
= 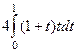 =
=  =
= 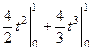 =
=
 =
= 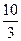 . Ответ.
. Ответ.  .
.
Задача 2. Вычислить интеграл 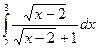 .
.
Решение. Сделаем замену 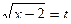 , тогда
, тогда 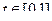 .
.
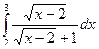 =
= 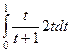 =
= 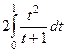 =
=  =
=
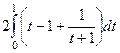 =
= 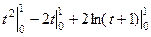 =
=  =
=  =
=  . Ответ.
. Ответ.  .
.
Задача 3. Вычислить интеграл 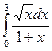 .
.
Решение. При замене 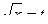 , если
, если  то
то  .
.
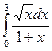 =
= 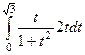 =
= 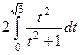 =
= 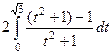 =
=
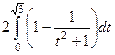 =
= 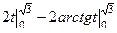 =
=  .
.
Ответ.  .
.
Рассмотрим 2 задачи на примерения интегрирования по частям в определённом интеграле.
Задача 4. Вычислить интеграл 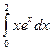 .
.
Решение. Применим метод интегрирования по частям,
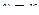
| 
|
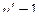
| 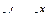
|
Тогда
 =
= 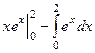 =
= 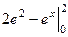 =
=  =
= 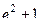 .
.
Ответ. 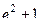 .
.
Задача 5. Вычислить интеграл 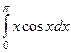 .
.
Решение. Тоже решается интегрированием по частям,
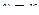 ,
, 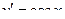 , тогда
, тогда 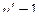 ,
,  .
.
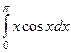 =
=  =
= 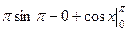 =
= 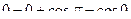 =
=  .
.
Ответ.  .
.
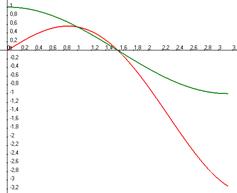
Замечание. Из строения графика видно, что ответ и должен был получиться отрицательным: изначально 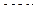 имеет две одинаковые части площади над и под осью, и его интеграл был бы 0, а если мы умножаем на
имеет две одинаковые части площади над и под осью, и его интеграл был бы 0, а если мы умножаем на 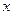 , то сильнее увеличится по модулю именно та часть, которая дальше от 0, то есть расположенная ниже горизонтальной оси. Вот эти графики, зелёным показан
, то сильнее увеличится по модулю именно та часть, которая дальше от 0, то есть расположенная ниже горизонтальной оси. Вот эти графики, зелёным показан 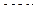 , красным
, красным 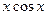 .
.
Задача 6. Вычислить интеграл 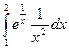 .
.
Решение. 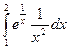 =
= 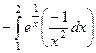 =
= 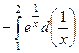
используя известное выражение 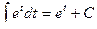 , получим:
, получим:
 =
= 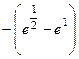 =
= 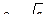 .
.
Задача 7. Вычислить интеграл 
Решение. Сделаем замену 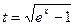 . Тогда
. Тогда 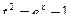 ,
, 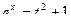 ,
, 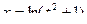 ,
, 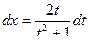 , функция
, функция  монотонна, так что замена корректная. Теперь найдём новые границы: если
монотонна, так что замена корректная. Теперь найдём новые границы: если  , то
, то 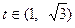 . Тогда
. Тогда 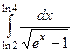 =
= 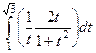 =
= 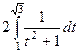 =
= 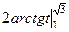 =
=  =
= 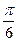 . Ответ.
. Ответ. 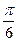 .
.
Задача 8. Вычислить интеграл  .
.
При этом осуществляется повторение темы «интегрирование тригонометрических функций».
Решение. Суммарная степень чётна, поэтому применяется замена
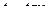 , тогда
, тогда  ,
, 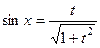 ,
, 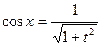 .
.
Пересчитаем границы. 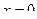
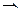
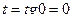 ,
, 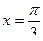
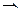
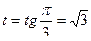 .
.
Итак, подставим всё это в интеграл.
 =
= 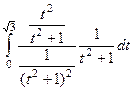 =
= 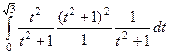 =
=
= 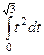 =
=  =
= 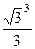 =
= 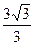 =
= 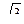 . Ответ.
. Ответ. 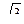 .
.
Задача 9. Вычислить интеграл 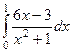 .
.
При этом осуществляется повторение темы «элементарные преобразования, подведение под знак дифференциала».
Решение. 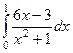 =
=  =
= 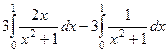 =
=
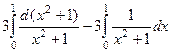 =
= 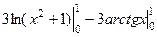 =
=
 =
= 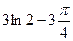 . Ответ.
. Ответ. 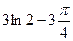 .
.
Задача 10. Вычислить интеграл 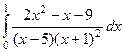 .
.
При этом осуществляется повторение темы «рациональные дроби».
Решение. Сначала представим дробь в виде суммы простейших.
 . При приведении к общему знаменателю, числитель получится такой:
. При приведении к общему знаменателю, числитель получится такой:
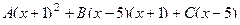 , что равно
, что равно  ,
, 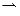
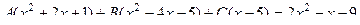
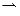
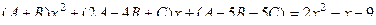
система: 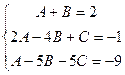 решим её методом Гаусса.
решим её методом Гаусса.
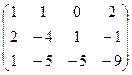
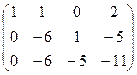
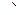
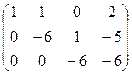 .
.
Здесь от 2-й строки отняли удвоенную 1-ю и от 3-й 1-ю, а затем от 3-й строки 2-ю. Основная матрица системы стала треугольной, и С находится сразу же:  . Тогда
. Тогда  и тогда
и тогда 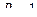 . Из 1-го уравнения тогда уже получается
. Из 1-го уравнения тогда уже получается  .
.
Значит, исходный интеграл распадается на сумму 3 интегралов: 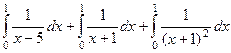 =
= 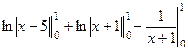 =
=
 =
=  =
= 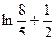 .
.
Ответ. 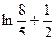 .
.
Задача 10* на повторение, либо домашняя.
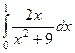 =
= 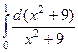 =
= 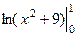 =
=  =
= 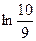 .
.

Типы оградительных сооружений в морском порту: По расположению оградительных сооружений в плане различают волноломы, обе оконечности...

Своеобразие русской архитектуры: Основной материал – дерево – быстрота постройки, но недолговечность и необходимость деления...

Историки об Елизавете Петровне: Елизавета попала между двумя встречными культурными течениями, воспитывалась среди новых европейских веяний и преданий...

История развития хранилищ для нефти: Первые склады нефти появились в XVII веке. Они представляли собой землянные ямы-амбара глубиной 4…5 м...
© cyberpedia.su 2017-2024 - Не является автором материалов. Исключительное право сохранено за автором текста.
Если вы не хотите, чтобы данный материал был у нас на сайте, перейдите по ссылке: Нарушение авторских прав. Мы поможем в написании вашей работы!