Аксель Туэ (1863 – 1922) – норвежский математик. Хотя он был специалистом по теории чисел, но остался в истории, как родоначальник теории формальных языков, связанные с решёнными им задачами о формальных словах известных теперь, как проблемы Туэ. Задачи решены в 1912 – 1914г.
I. Введём следующие определения.
1) Сформулируем определение 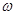 - слова:
- слова:
Бесконечная последовательность элементов алфавита А называется 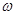 - словом или сверхсловом. Таким образом,
- словом или сверхсловом. Таким образом, 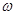 - слово может быть отождествлено с отображением множества целых чисел в А. Очень удобным средством задания конкретных
- слово может быть отождествлено с отображением множества целых чисел в А. Очень удобным средством задания конкретных 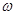 - слов являются DOL – системы.
- слов являются DOL – системы.
2) Тройка G = (A, h, w), A – алфавит, 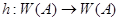 - морфизм и w – слово над А, называется DOL – системой. DOL – система G определяет S(G) слов над А:
- морфизм и w – слово над А, называется DOL – системой. DOL – система G определяет S(G) слов над А:
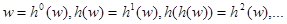 .
.
Рассмотрим DOL – систему G = (A, h, w), такую, что 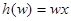 , х
, х 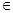 Z(A), т.е. w – собственное начало слова h(w) и, кроме того, h является нестирающим (т.е. h(a)=
Z(A), т.е. w – собственное начало слова h(w) и, кроме того, h является нестирающим (т.е. h(a)= 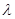 для всех а из А). Тогда
для всех а из А). Тогда
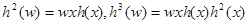 и вообще
и вообще
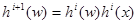 для всех i
для всех i 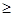 0.
0.
Последнее равенство показывает, что 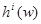 для всех i является собственным началом слова
для всех i является собственным началом слова 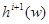 . Следовательно,
. Следовательно, 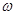 - слово
- слово 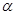 может быть определено как “ предел ” последовательности
может быть определено как “ предел ” последовательности 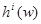 , i=0,1,2, …. Точнее,
, i=0,1,2, …. Точнее, 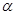 представляет собой
представляет собой 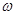 - слово, начало которого, имеющее длину
- слово, начало которого, имеющее длину  , есть
, есть 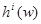 , i=0,1,2, ….
, i=0,1,2, ….
3) Определение. Слово или 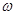 - слово называется бесквадратным (бескубным), если оно не содержит подслова вида хх (соответственно х
- слово называется бесквадратным (бескубным), если оно не содержит подслова вида хх (соответственно х 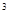 ), где х – непустое слово.
), где х – непустое слово.
Слово или 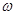 - слово называется сильно бескубным, если если оно не содержит слов вида хх а, где х – непустое слово, а а – первая буква слова х.
- слово называется сильно бескубным, если если оно не содержит слов вида хх а, где х – непустое слово, а а – первая буква слова х.
4) Может случиться, что слово w содержит два “перекрывающихся” вхождения х, т.е. подслово xy = zx, где 
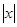 . Если это не имеет место, то будем называть w словом без перекрытий.
. Если это не имеет место, то будем называть w словом без перекрытий.
II. Сформулируем основные теоремы.
Рассмотрим следующую DOL – систему G = ({a, b}, h, a), где h определяется следующим образом: h(a) =ab, h(b) = ba. Тогда последовательность S(G) начинается словами:
a, ab, abba, abba baab, abba baab baab abba, ….
Теперь 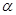 есть
есть 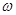 - слово, порожденное DOL – системой G.
- слово, порожденное DOL – системой G.
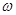 - слово
- слово 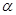 является сильно бескубным.
является сильно бескубным.
Сформулируем следующее:
Существует бесквадратное 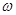 - слово
- слово 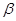 над алфавитом из четырех символов и cуществует бесквадратное
над алфавитом из четырех символов и cуществует бесквадратное 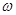 - слово
- слово  над алфавитом из трёх символов .
над алфавитом из трёх символов .
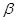 =
=  где
где 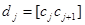 для всех j
для всех j 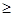 1.
1.
Введём новые обозначения для элементов А1, положив
[aa] = 1, [ab] = 2, [ba] = 3, [bb] = 4.
Теперь начало 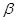 имеет вид
имеет вид
2432312431232432312324312432312…
Рассмотрим алфавит А2 = {1, 2, 3}. Определим 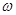 - слово
- слово 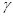 кА результат замены в
кА результат замены в 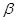 всех вхождений символа 4 символом 1.
всех вхождений символа 4 символом 1.
Теперь подведём итог полному решению проблемы Туэ в следующих теоремах:
1) “Если А состоит не менее чем из трёх символов, то над А существует бесквадратное 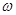 - слово ”;
- слово ”;
2) “Если А имеем не менее двух символов, то А существует сильно бескубное, а значит и бескубное 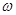 - слово”.
- слово”.
III.Сейчас рассмотрим некоторые методы доказательства.
В формулировках основных теорем показано, как строятся 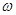 - слова
- слова 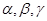 .
.
Теорема 3.1.
Слово и 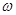 - слово свободно от перекрытий тогда и только тогда, когда оно является сильно бескубным.
- слово свободно от перекрытий тогда и только тогда, когда оно является сильно бескубным.
Доказательство. Пусть w не свободно от перекрытий. Тогда w найдется подслово xy = zx, такое, что имеет место 
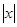 . Пусть а – первая буква слова z. По нашему предположению, x = zx
. Пусть а – первая буква слова z. По нашему предположению, x = zx 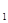 , где первой буквой слова x
, где первой буквой слова x 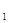 также будет а. Следовательно, zza – подслово w и w не является сильно бескубеым.
также будет а. Следовательно, zza – подслово w и w не является сильно бескубеым.
Наоборот, предположим, что w не является сильно бескубным. Тогда в w найдётся слово z 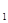 z
z 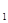 a, где а – первая буква z
a, где а – первая буква z 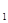 . Пологая z
. Пологая z 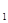 =аz
=аz 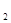 мы видим, что х = а z
мы видим, что х = а z 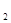 а, y = z
а, y = z 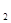 а, z = а z
а, z = а z 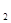 . Тогда xy = zx – подслово w, и, кроме того, выполняется
. Тогда xy = zx – подслово w, и, кроме того, выполняется 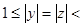
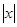 . Отсюда следует, что w не свободно от перекрытий. Ч.т.д.
. Отсюда следует, что w не свободно от перекрытий. Ч.т.д.
Теорема 3.2.
Ни одно слово, имеющее длину более 3, над алфавитом А из двух букв не является бесквадратным. Следовательно, над алфавиотм А не существует бесквадратных 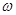 - слов.
- слов.
Доказательство. Пусть А состоит из букв a и b. Существуют только 2 бесквадратных слова
аbа и bаb, (*)
так как все другие слова указанной длины:
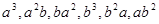
содержит в качестве подслова либо 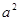 , либо
, либо 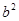 . С другой стороны, каким бы способом ни была приписана буква к любому слову из (*), результирующее слово в каждом случае будет содержать в качестве подслова одно из слов
. С другой стороны, каким бы способом ни была приписана буква к любому слову из (*), результирующее слово в каждом случае будет содержать в качестве подслова одно из слов 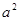 ,
, 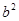 ,
,  и, следовательно, не будет бесквадратным.Ч.т.д.
и, следовательно, не будет бесквадратным.Ч.т.д.
Теоремя 3.3.
Ни 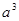 , ни
, ни 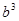 не входят в качестве подслова в
не входят в качестве подслова в 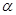 . Ни ababa, ни babab не входят в качестве подслова в
. Ни ababa, ни babab не входят в качестве подслова в 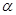 . Следовательно, любое подслово х
. Следовательно, любое подслово х 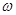 - слова
- слова 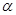
 , такое, что
, такое, что 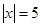 , содержит в качестве подслова либо
, содержит в качестве подслова либо 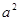 , либо
, либо 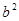 .
.
Доказательство. Докажем первое утверждение. Если слово 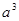 или
или 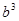 входит в качестве подслова в
входит в качестве подслова в 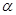 , то оно входит в качестве подслова в некоторое w
, то оно входит в качестве подслова в некоторое w  . Но это не возможно, так как w
. Но это не возможно, так как w 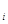 = h(w
= h(w 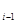 ) и, следовательно, w
) и, следовательно, w 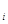 получено приписыванием слов ab и ba в некотором порядке.
получено приписыванием слов ab и ba в некотором порядке.
Докажем второе утверждение. Предположим, что ababa входит в качестве подслова в 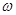 - слова
- слова 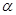 , начиная с j-й его буквы. Тогда используя
, начиная с j-й его буквы. Тогда используя 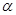 =
= 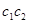 …, запишем
…, запишем
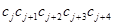 = ababa. (**)
= ababa. (**)
Выберем настолько большое j что 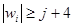 . Тогда вхождения (**) целиком лежит в w
. Тогда вхождения (**) целиком лежит в w 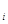 .Ещё раз используя соотношение w
.Ещё раз используя соотношение w 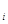 = h(w
= h(w 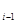 ), заключаем, что в w
), заключаем, что в w 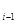 в качестве подслова входит либо
в качестве подслова входит либо 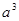 , либо
, либо 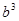 в зависимости от того, является ли j в (**) нечетным или четным. Но это не возможно в силу доказанного выше первого утверждения. Аналогично и для babab не входит в
в зависимости от того, является ли j в (**) нечетным или четным. Но это не возможно в силу доказанного выше первого утверждения. Аналогично и для babab не входит в 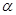 .
.
Наконец, последнее утверждение является следствием второго, так как, за исключением слов ababa и babab, любое слово длины 5 над {a,b} содержит в качестве подслова либо 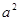 , либо
, либо 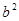 . Ч.т.д.
. Ч.т.д.
Теорема 3.4.
Предположим, что 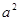 или
или 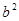 входит в качестве подслова в
входит в качестве подслова в 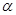 , начиная с j-й; тогда j четно.
, начиная с j-й; тогда j четно.
Доказательство. Используя обозначения предыдущей теоремы, предположим, что  есть
есть 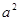 или
или 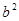 . Вновь выбираем такое i, что
. Вновь выбираем такое i, что 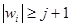 , и применяем соотношение w
, и применяем соотношение w 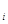 = h(w
= h(w 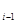 ). В силу этого соотношения, если j нечетно, то
). В силу этого соотношения, если j нечетно, то  есть либо h(a), либо h(b). Так как ни h(a), ни h(b) не есть
есть либо h(a), либо h(b). Так как ни h(a), ни h(b) не есть 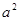 или
или 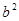 .Ч.т.д.
.Ч.т.д.
Литература
1. Курош А.Т. Лекции по общей алгебре. – М.: Наука, 1973.
2. Лаллеман Ж. Полугруппы и комбинаторные приложения. – М.: Мир, 1985.
3. Саломаа А. Жемчужины теории формальных языков. – М.: Мир, 1986.
4. Скорняков Л.А. Элементы алгебры. – М.: Наука, 1986.



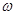 - слова:
- слова: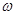 - словом или сверхсловом. Таким образом,
- словом или сверхсловом. Таким образом, 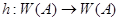 - морфизм и w – слово над А, называется DOL – системой. DOL – система G определяет S(G) слов над А:
- морфизм и w – слово над А, называется DOL – системой. DOL – система G определяет S(G) слов над А: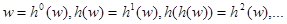 .
.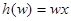 , х
, х 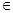 Z(A), т.е. w – собственное начало слова h(w) и, кроме того, h является нестирающим (т.е. h(a)=
Z(A), т.е. w – собственное начало слова h(w) и, кроме того, h является нестирающим (т.е. h(a)= 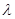 для всех а из А). Тогда
для всех а из А). Тогда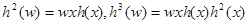 и вообще
и вообще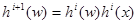 для всех i
для всех i 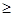 0.
0.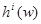 для всех i является собственным началом слова
для всех i является собственным началом слова 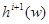 . Следовательно,
. Следовательно, 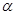 может быть определено как “ предел ” последовательности
может быть определено как “ предел ” последовательности  , есть
, есть 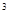 ), где х – непустое слово.
), где х – непустое слово.
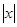 . Если это не имеет место, то будем называть w словом без перекрытий.
. Если это не имеет место, то будем называть w словом без перекрытий.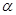 есть
есть 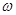 - слово, порожденное DOL – системой G.
- слово, порожденное DOL – системой G.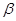 над алфавитом из четырех символов и cуществует бесквадратное
над алфавитом из четырех символов и cуществует бесквадратное  над алфавитом из трёх символов .
над алфавитом из трёх символов .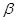 =
=  где
где 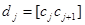 для всех j
для всех j 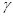 кА результат замены в
кА результат замены в 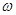 - слова
- слова 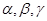 .
.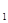 , где первой буквой слова x
, где первой буквой слова x 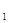 также будет а. Следовательно, zza – подслово w и w не является сильно бескубеым.
также будет а. Следовательно, zza – подслово w и w не является сильно бескубеым.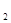 мы видим, что х = а z
мы видим, что х = а z 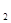 а, z = а z
а, z = а z 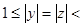
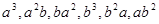
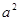 , либо
, либо 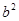 . С другой стороны, каким бы способом ни была приписана буква к любому слову из (*), результирующее слово в каждом случае будет содержать в качестве подслова одно из слов
. С другой стороны, каким бы способом ни была приписана буква к любому слову из (*), результирующее слово в каждом случае будет содержать в качестве подслова одно из слов 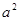 ,
,  и, следовательно, не будет бесквадратным.Ч.т.д.
и, следовательно, не будет бесквадратным.Ч.т.д.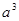 , ни
, ни 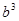 не входят в качестве подслова в
не входят в качестве подслова в 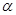
 , такое, что
, такое, что 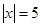 , содержит в качестве подслова либо
, содержит в качестве подслова либо 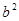 .
. . Но это не возможно, так как w
. Но это не возможно, так как w 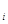 = h(w
= h(w 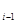 ) и, следовательно, w
) и, следовательно, w 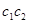 …, запишем
…, запишем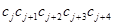 = ababa. (**)
= ababa. (**)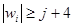 . Тогда вхождения (**) целиком лежит в w
. Тогда вхождения (**) целиком лежит в w 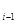 в качестве подслова входит либо
в качестве подслова входит либо  есть
есть 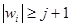 , и применяем соотношение w
, и применяем соотношение w 


