

Кормораздатчик мобильный электрифицированный: схема и процесс работы устройства...

Общие условия выбора системы дренажа: Система дренажа выбирается в зависимости от характера защищаемого...

Кормораздатчик мобильный электрифицированный: схема и процесс работы устройства...

Общие условия выбора системы дренажа: Система дренажа выбирается в зависимости от характера защищаемого...
Топ:
Техника безопасности при работе на пароконвектомате: К обслуживанию пароконвектомата допускаются лица, прошедшие технический минимум по эксплуатации оборудования...
Отражение на счетах бухгалтерского учета процесса приобретения: Процесс заготовления представляет систему экономических событий, включающих приобретение организацией у поставщиков сырья...
Методика измерений сопротивления растеканию тока анодного заземления: Анодный заземлитель (анод) – проводник, погруженный в электролитическую среду (грунт, раствор электролита) и подключенный к положительному...
Интересное:
Инженерная защита территорий, зданий и сооружений от опасных геологических процессов: Изучение оползневых явлений, оценка устойчивости склонов и проектирование противооползневых сооружений — актуальнейшие задачи, стоящие перед отечественными...
Влияние предпринимательской среды на эффективное функционирование предприятия: Предпринимательская среда – это совокупность внешних и внутренних факторов, оказывающих влияние на функционирование фирмы...
Уполаживание и террасирование склонов: Если глубина оврага более 5 м необходимо устройство берм. Варианты использования оврагов для градостроительных целей...
Дисциплины:
|
из
5.00
|
Заказать работу |
|
|
|
|
Показательные уравнения
Уравнение, содержащее переменную в показателе степени, называется показательным. Простейшим примером показательного уравнения служит уравнение ах = b (a >0, а ¹1).
Решение показательного уравнения вида af (x)= ag (x) (a >0, а ¹1) основано на том, что это уравнение равносильно уравнению f (x)= g (x).
Следствие. Пусть a >0, а ¹1. Если степени с основанием а равны, то их показатели равны, т.е. если as = at, то s = t.
Приведение обеих частей уравнения к одному основанию
Этот способ основан на свойстве степеней: если две степени равны и их основания равны, то равны и их показатели.
Пример 1. Решите уравнение 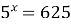 .
.
Решение. 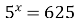 ;
; 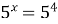 ; х =4.
; х =4.
Ответ: 4
Пример 2. Найдите корень уравнения  .
.
Решение. Перейдем к одному основанию степени: 

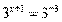

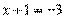

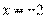 .
.
Ответ: 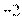
Задание 1. Решите уравнение…
1) 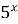 =125 =125
| 2) 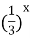 = = 
| 3) 27 х = 
| 4)  = ‑2 = ‑2
| 5)  =625 =625
|
6) 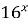 = = 
| 7) 6 х =1296 | 8)  =8 =8
| 9) 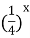 = = 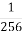
| 10) 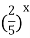 = ‑2,5 = ‑2,5
|
Пример 3. Решите уравнение 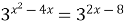 .
.
Решение. Данное уравнение равносильно уравнению 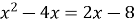 или
или 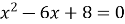 .
.
Решая квадратное уравнение, находим х 1=2, х 2=4. Эти числа являются корнями исходного показательного уравнения.
Ответ: 2; 4
Задание 2. Решите уравнение…
1) 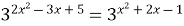
| 2) 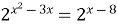
| 3) 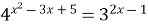
|
4) 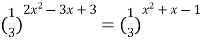
| 5) 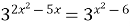
| 6) 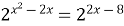
|
7) 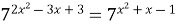
| 8) 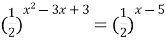
| 9) 
|
10) 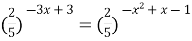
|
Пример 4. Решите уравнение 102 х ‑ 5=100.
Решение. 102 х ‑ 5=100; 102 х ‑ 5=102; 2 х ‑ 5=2; отсюда х =3,5.
Ответ: 3,5
Пример 5. Найдите корень уравнения  .
.
Решение. Перейдем к одному основанию степени: 

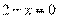

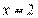 .
.
Ответ: 2
Задание 3. Решите уравнение…
| 1) 35 – 2 х =81 | 2) 48+5 х =1 | 3) 32 – х =27 | 4) 4 х 2+ х =16 | 5) 2 х +2=128 |
| 6) 2 х +1=16 | 7) 2 х – 1=32 | 8) 3 х 2 – х =1 | 9) 9 – х =27 | 10) 4 – х =16 |
Пример 6. Решите уравнение 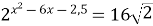 .
.
Решение. Уравнение решается приведением левой и правой частей к степеням с равными основаниями. 16 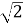 =24×21/2=24,5.
=24×21/2=24,5.
Из уравнения 2 х 2‑6 х ‑2,5=24,5 получаем х 2‑6 х ‑2,5=4,5, откуда х = ‑1 и х =7.
|
|
Ответ: ‑ 1; 7
Пример 7. Найдите корень уравнения  .
.
Решение. Перейдем к одному основанию степени: 

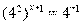



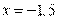 .
.
Ответ: 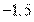
Пример 8. Найдите корень уравнения  .
.
Решение. Приведем обе части уравнения к основанию 3: 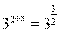

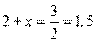

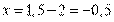 .
.
Ответ: 
Задание 4. Решите уравнение…
1) 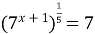
| 2) 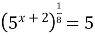
| 3) 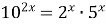
| 4) 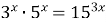
|
5) 
| 6) 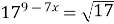
| 7) 
| 8) 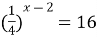
|
9) 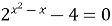
| 10) 
| 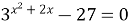
|
Пример 9. Решите уравнение 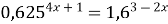 .
.
Решение. Приведем обе части уравнения к одному основанию:
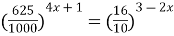 ;
; 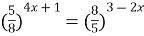 ;
; 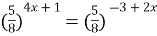 ;
;
 ;
; 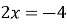 ; x = ‑ 2.
; x = ‑ 2.
Ответ: ‑ 2
Пример 10. Найдите корень уравнения 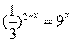 .
.
Решение. Перейдем к одному основанию степени: 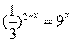

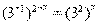

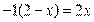

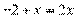

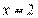 .
.
Ответ: 2
Пример 11. Найдите корень уравнения 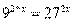 .
.
Решение. Приведем обе части уравнения к основанию 3: 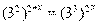



 .
.
Ответ: 1
Задание 5. Решите уравнение…
1) 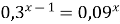
| 2) 
| 3)  = = 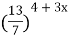
| 4) 
|
5) 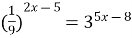
| 6) 
| 7) 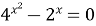
| 8) 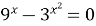
|
9) 
| 10) 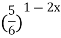 = = 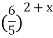
|
Пример 12. Решите уравнение 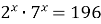 .
.
Решение. Воспользуемся свойством степени:
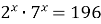 ;
; 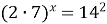 ;
; 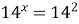 . Отсюда х =2.
. Отсюда х =2.
Ответ: 2
Задание 6. Решите уравнение…
1) 
| 2) 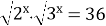
| 3) 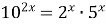
| 4) 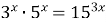
|
5) 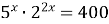
| 6) 
| 7) 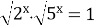
| 8) 
|
9) 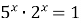
| 10) 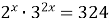
|
Пример 13. Решите уравнение  .
.
Решение.  ;
; 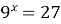 ;
; 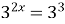 ; 2 x =3; x =
; 2 x =3; x =  .
.
Ответ: 
Пример 14. Найдите корень уравнения 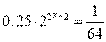 .
.
Решение. Приведем обе части уравнения к основанию 2: 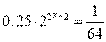

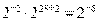





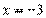 .
.
Ответ: 
Пример 15. Найдите корень уравнения 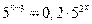 .
.
Решение. Преобразуем правую часть уравнения:  .
.
Получаем уравнение 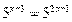

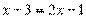

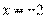
Ответ: 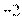
Задание 7. Решите уравнение…
1) 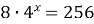
| 2) 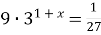
| 3) 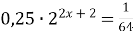
| 4) 
|
5) 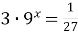
| 6) 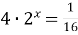
| 7) 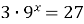
| 8) 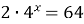
|
9) 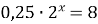
| 10) 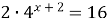
|
Пример 16. Решите уравнение 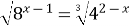 .
.
Решение. По определению корня имеем: 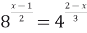 .
.
Приведем обе части уравнения к одному основанию:
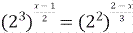 ;
; 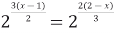 .
.
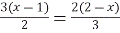 ; 9(x – 1)=4(2 – x); 9 x – 9=8 – 4 x; 13 x =17; x =
; 9(x – 1)=4(2 – x); 9 x – 9=8 – 4 x; 13 x =17; x = 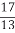 .
.
Ответ: 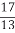
Задание 8. Решите уравнение…
1)  = = 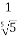
| 2)  =4 =4
| 3) 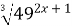 = = 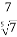
| 4) 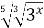 =27 =27
|
5)  = = 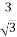
| 6) (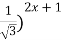 = = 
| 7) 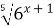 = = 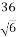
| 8) 16 ‑1 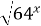 =2x =2x
|
9) (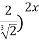 = = 
| 10) 8 ‑1 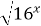 =2x/2 =2x/2
|
Пример 17. Решите уравнение 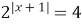 .
.
Решение. 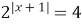 ;
;  ; |x+1|=2 Û
; |x+1|=2 Û 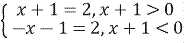 Û
Û
Û 
Ответ: 1; ‑ 3
Задание 9. Решите уравнение…
1) 
| 2) 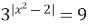
| 3) 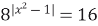
| 4) 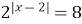
|
5) 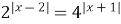
| 6) 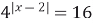
| 7) 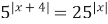
| 8) 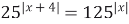
|
9) 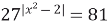
| 10) 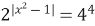
|
Пример 18. Решите уравнение 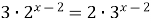 .
.
Решение. 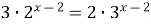 ;
; 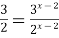 ; 1= x – 2; x =3.
; 1= x – 2; x =3.
Ответ: 3
Задание 10. Решите уравнение…
1) 
| 2) 
|
3) 
| 4) 
|
5) 
| 6) 
|
7) 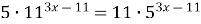
| 8) 
|
9) 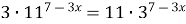
| 10) 
|
Метод почленного деления
Суть метода в почленном делении уравнения, члены которого представляют собой степени с одинаковыми показателями и различными основаниями на одну из степеней.
|
|
При этом удобнее делить на степень с большим показателем.
Пример 28. Решите уравнение 9х+6х=2×4х.
Решение. Разделим обе части уравнения на 4х≠0, получим 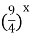 +
+  =2,
=2, 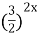 +
+ 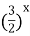 ‑2=0. Обозначим
‑2=0. Обозначим 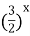 = у, у >0, получим у 2+ у ‑2=0; y 1= ‑2; у 2=1. ‑2 не удовлетворяет условию у >0. Имеем
= у, у >0, получим у 2+ у ‑2=0; y 1= ‑2; у 2=1. ‑2 не удовлетворяет условию у >0. Имеем 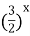 =1. х =0.
=1. х =0.
Ответ: 0
Задание 16. Решите уравнение…
1) 
| 2) 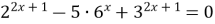
|
3) 
| 4) 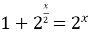
|
5) 
| 6) 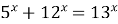
|
7) 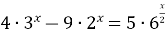
| 8) 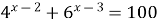
|
Логарифмирование
Уравнения вида a f(x)= b g(x) (a >0, a ≠1, b >0, b ≠1), где f (x) и g (x) – элементарные функции, решаются логарифмированием обеих частей.
Уравнения вида 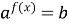 , где a >0, a ¹1 имеет решение, если b > 0. Его решают логарифмированием по основанию a:
, где a >0, a ¹1 имеет решение, если b > 0. Его решают логарифмированием по основанию a: 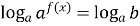 . Тогда
. Тогда 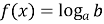 .
.
Пример 29. Решить уравнение  .
.
Решение. Прологарифмируем уравнение по основанию 3.
Получаем: 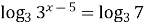 ;
;  ;
; 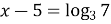 ;
; 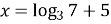 .
.
Ответ: 
Задание 17. Решите уравнение…
1) 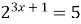
| 2) 
| 3) 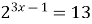
| 4) 
|
5) 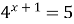
| 6) 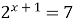
| 7) 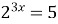
| 8) 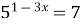
|
9) 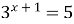
| 10) 
|
Пример 30. Решите уравнение 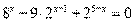 ; Найдите все корни этого уравнения, принадлежащие промежутку
; Найдите все корни этого уравнения, принадлежащие промежутку 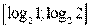 .
.
Решение. Умножим обе части уравнения на положительное выражение 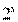 , получим:
, получим: 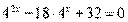 , откуда
, откуда  и
и  .
.
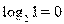 ,
, 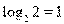 , значит, указанному промежутку принадлежит только корень
, значит, указанному промежутку принадлежит только корень  .
.
Ответ: 0,5; 2 и 2; 0,5
Пример 31. Решите уравнение 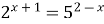 .
.
Решение. Поскольку 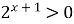 и
и 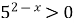 при любых значениях х, то можно прологарифмировать обе части данного уравнения, например, по основанию 2:
при любых значениях х, то можно прологарифмировать обе части данного уравнения, например, по основанию 2:
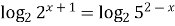 ;
;  .
.
Далее раскроем скобки и выразим х: х +1=(2 – х) 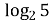 , откуда х + х
, откуда х + х  =2
=2 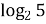 – 1, x =
– 1, x = 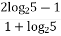 .
.
Ответ: 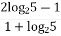
Задание 18. Решите уравнение…
1) 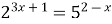
| 2) 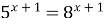
| 3) 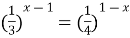
| 4) 
|
5) 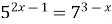
| 6) 
| 7) 
| 8) 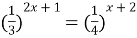
|
9) 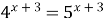
| 10) 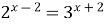
|
Уравнения с параметром
Пример 33. Найти все значения параметра а, при которых уравнение 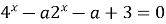 имеет хотя бы одно решение.
имеет хотя бы одно решение.
Решение. Сделаем замену 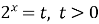 . Тогда исходное уравнение примет вид
. Тогда исходное уравнение примет вид 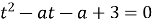 . Для того чтобы оно имело хотя бы одно решение, необходимо и достаточно, чтобы квадратный трехчлен имел хотя бы один положительный корень, значит дискриминант должен быть больше нуля.
. Для того чтобы оно имело хотя бы одно решение, необходимо и достаточно, чтобы квадратный трехчлен имел хотя бы один положительный корень, значит дискриминант должен быть больше нуля.
Поскольку 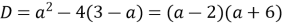 , то условие D ³0 выполняется при а ³2 или а £ ‑ 6.
, то условие D ³0 выполняется при а ³2 или а £ ‑ 6.
По теореме Виета, корни уравнения 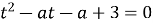 удовлетворяют системе уравнений
удовлетворяют системе уравнений 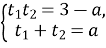 .
.
При а £ ‑ 6 имеем 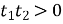 , а
, а 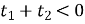 , поэтому оба корня отрицательны, и, следовательно, исходное уравнение решений не имеет.
, поэтому оба корня отрицательны, и, следовательно, исходное уравнение решений не имеет.
При а ³2 имеем 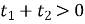 , следовательно, хотя бы один из корней больше нуля.
, следовательно, хотя бы один из корней больше нуля.
Таким образом, уравнение имеет хотя бы одно решение при а ³2.
Ответ: [2; +∞)
Пример 34. Найти все значения параметра 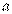 , при которых уравнение
, при которых уравнение 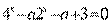 имеет хотя бы одно решение.
имеет хотя бы одно решение.
|
|
Решение. Сделаем замену 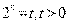 . Тогда исходное уравнение примет вид
. Тогда исходное уравнение примет вид 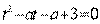 . Для того чтобы оно имело хотя бы одно решение, необходимо и достаточно, чтобы квадратный трехчлен имел хотя бы один положительный корень, значит дискриминант должен быть больше нуля.
. Для того чтобы оно имело хотя бы одно решение, необходимо и достаточно, чтобы квадратный трехчлен имел хотя бы один положительный корень, значит дискриминант должен быть больше нуля.
Поскольку 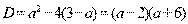 , то условие
, то условие 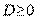 выполняется при
выполняется при 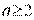 или
или 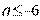 .
.
По теореме Виета, корни уравнения 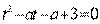 удовлетворяют системе уравнений
удовлетворяют системе уравнений 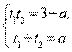 .
.
При 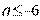 имеем
имеем 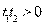 , а
, а 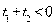 , поэтому оба корня отрицательны, и, следовательно, исходное уравнение решений не имеет.
, поэтому оба корня отрицательны, и, следовательно, исходное уравнение решений не имеет.
При 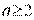 имеем
имеем 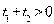 , следовательно, хотя бы один из корней больше нуля. Таким образом, уравнение имеет хотя бы одно решение при
, следовательно, хотя бы один из корней больше нуля. Таким образом, уравнение имеет хотя бы одно решение при 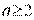 .
.
Ответ: 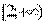
Пример 35. Найдите все значения 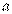 , при каждом из которых уравнение
, при каждом из которых уравнение 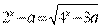 имеет единственный корень.
имеет единственный корень.
Решение. Пусть 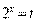 .
. 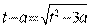 ;
; 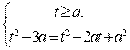 ;
; 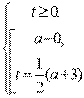 ;
; 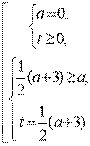 ;
; 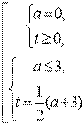 .
.
Так как 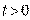 , получаем если
, получаем если 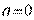 , то
, то 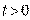 ; если
; если 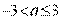 , то
, то 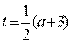 . Поскольку при
. Поскольку при 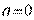 решением являются все положительные значения
решением являются все положительные значения 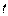 , уравнение имеет единственное решение, если
, уравнение имеет единственное решение, если 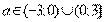
Ответ: 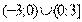
Задание 20. При каких значениях а уравнение…
| 1) 25х+5х×(2 ‑ 3 а)+2 а 2 ‑ 5 а ‑ 3=0 имеет одно решение |
| 2) 9х ‑ 3х×(5 а +3)+6 а 2 +11 а ‑ 10=0 имеет одно решение |
| 3) 4х ‑ 2х×(6 а ‑ 4)+5 а 2 – 4 а =0 имеет два различных решения |
| 4) 36х+6х×(а ‑ 1) ‑ 2 а 2 + а =0 имеет два различных решения |
5) 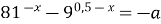 имеет два различных решения имеет два различных решения
|
6) 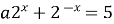 имеет единственное решение имеет единственное решение
|
7) 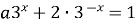 имеет единственное решение имеет единственное решение
|
8) 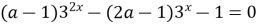 имеет два различных решения имеет два различных решения
|
9) 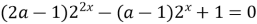 имеет два различных решения имеет два различных решения
|
10) 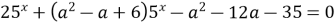 не имеет решений не имеет решений
|
Показательные уравнения
Уравнение, содержащее переменную в показателе степени, называется показательным. Простейшим примером показательного уравнения служит уравнение ах = b (a >0, а ¹1).
Решение показательного уравнения вида af (x)= ag (x) (a >0, а ¹1) основано на том, что это уравнение равносильно уравнению f (x)= g (x).
Следствие. Пусть a >0, а ¹1. Если степени с основанием а равны, то их показатели равны, т.е. если as = at, то s = t.
Приведение обеих частей уравнения к одному основанию
Этот способ основан на свойстве степеней: если две степени равны и их основания равны, то равны и их показатели.
Пример 1. Решите уравнение 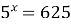 .
.
Решение. 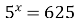 ;
; 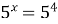 ; х =4.
; х =4.
Ответ: 4
Пример 2. Найдите корень уравнения  .
.
Решение. Перейдем к одному основанию степени: 

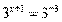

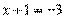

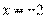 .
.
|
|
Ответ: 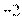
Задание 1. Решите уравнение…
1) 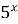 =125 =125
| 2) 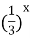 = = 
| 3) 27 х = 
| 4)  = ‑2 = ‑2
| 5)  =625 =625
|
6) 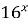 = = 
| 7) 6 х =1296 | 8)  =8 =8
| 9) 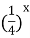 = = 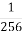
| 10) 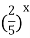 = ‑2,5 = ‑2,5
|
Пример 3. Решите уравнение 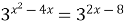 .
.
Решение. Данное уравнение равносильно уравнению 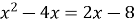 или
или 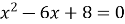 .
.
Решая квадратное уравнение, находим х 1=2, х 2=4. Эти числа являются корнями исходного показательного уравнения.
Ответ: 2; 4
Задание 2. Решите уравнение…
1) 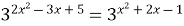
| 2) 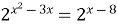
| 3) 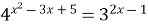
|
4) 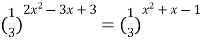
| 5) 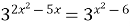
| 6) 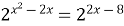
|
7) 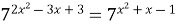
| 8) 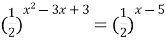
| 9) 
|
10) 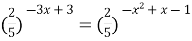
|
Пример 4. Решите уравнение 102 х ‑ 5=100.
Решение. 102 х ‑ 5=100; 102 х ‑ 5=102; 2 х ‑ 5=2; отсюда х =3,5.
Ответ: 3,5
Пример 5. Найдите корень уравнения  .
.
Решение. Перейдем к одному основанию степени: 

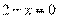

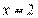 .
.
Ответ: 2
Задание 3. Решите уравнение…
| 1) 35 – 2 х =81 | 2) 48+5 х =1 | 3) 32 – х =27 | 4) 4 х 2+ х =16 | 5) 2 х +2=128 |
| 6) 2 х +1=16 | 7) 2 х – 1=32 | 8) 3 х 2 – х =1 | 9) 9 – х =27 | 10) 4 – х =16 |
Пример 6. Решите уравнение 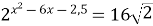 .
.
Решение. Уравнение решается приведением левой и правой частей к степеням с равными основаниями. 16 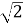 =24×21/2=24,5.
=24×21/2=24,5.
Из уравнения 2 х 2‑6 х ‑2,5=24,5 получаем х 2‑6 х ‑2,5=4,5, откуда х = ‑1 и х =7.
Ответ: ‑ 1; 7
Пример 7. Найдите корень уравнения  .
.
Решение. Перейдем к одному основанию степени: 

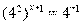



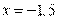 .
.
Ответ: 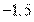
Пример 8. Найдите корень уравнения  .
.
Решение. Приведем обе части уравнения к основанию 3: 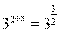

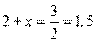

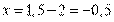 .
.
Ответ: 
Задание 4. Решите уравнение…
1) 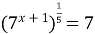
| 2) 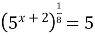
| 3) 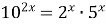
| 4) 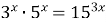
|
5) 
| 6) 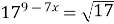
| 7) 
| 8) 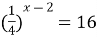
|
9) 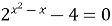
| 10) 
| 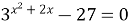
|
Пример 9. Решите уравнение 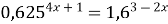 .
.
Решение. Приведем обе части уравнения к одному основанию:
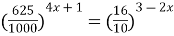 ;
; 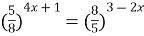 ;
; 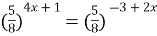 ;
;
 ;
; 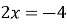 ; x = ‑ 2.
; x = ‑ 2.
Ответ: ‑ 2
Пример 10. Найдите корень уравнения 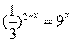 .
.
Решение. Перейдем к одному основанию степени: 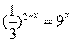

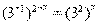

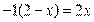

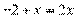

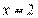 .
.
Ответ: 2
Пример 11. Найдите корень уравнения 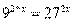 .
.
Решение. Приведем обе части уравнения к основанию 3: 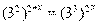



 .
.
Ответ: 1
Задание 5. Решите уравнение…
1) 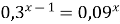
| 2) 
| 3)  = = 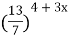
| 4) 
|
5) 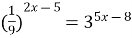
| 6) 
| 7) 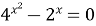
| 8) 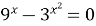
|
9) 
| 10) 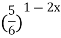 = = 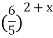
|
Пример 12. Решите уравнение 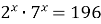 .
.
Решение. Воспользуемся свойством степени:
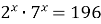 ;
; 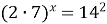 ;
; 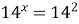 . Отсюда х =2.
. Отсюда х =2.
Ответ: 2
Задание 6. Решите уравнение…
1) 
| 2) 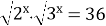
| 3) 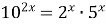
| 4) 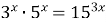
|
5) 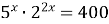
| 6) 
| 7) 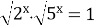
| 8) 
|
9) 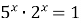
| 10) 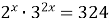
|
Пример 13. Решите уравнение  .
.
Решение.  ;
; 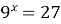 ;
; 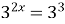 ; 2 x =3; x =
; 2 x =3; x =  .
.
Ответ: 

Археология об основании Рима: Новые раскопки проясняют и такой острый дискуссионный вопрос, как дата самого возникновения Рима...

Своеобразие русской архитектуры: Основной материал – дерево – быстрота постройки, но недолговечность и необходимость деления...

Механическое удерживание земляных масс: Механическое удерживание земляных масс на склоне обеспечивают контрфорсными сооружениями различных конструкций...

Двойное оплодотворение у цветковых растений: Оплодотворение - это процесс слияния мужской и женской половых клеток с образованием зиготы...
© cyberpedia.su 2017-2024 - Не является автором материалов. Исключительное право сохранено за автором текста.
Если вы не хотите, чтобы данный материал был у нас на сайте, перейдите по ссылке: Нарушение авторских прав. Мы поможем в написании вашей работы!