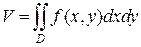Двойные интегралы
- Основные понятия и определения
Обобщением определенного интеграла на случай функций двух переменных является так называемый двойной интеграл.
Пусть в прямоугольной области 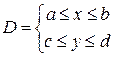 задана непрерывная функция
задана непрерывная функция 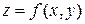 .Разобьем область
.Разобьем область  прямоугольной сеткой
прямоугольной сеткой
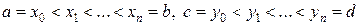
на «элементарные области» 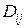 (
(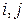 =
= 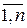 ), площади которых равны
), площади которых равны 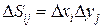 . Диаметром элементарной области
. Диаметром элементарной области 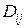 будем называть диагональ прямоугольника
будем называть диагональ прямоугольника 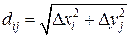 . В каждой такой области выберем произвольную точку
. В каждой такой области выберем произвольную точку 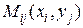 , умножим значение функции
, умножим значение функции 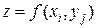 в этой точке на
в этой точке на 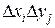 и составим сумму всех таких произведений:
и составим сумму всех таких произведений:
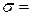
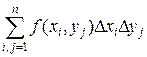 . (1)
. (1)
Эта сумма называется интегральной суммой функции 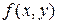 .Рассмотрим предел интегральной суммы (1), когда
.Рассмотрим предел интегральной суммы (1), когда 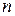 стремится к бесконечности таким образом, что
стремится к бесконечности таким образом, что 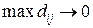 . Если этот предел существует и не зависит ни от способа разбиения области
. Если этот предел существует и не зависит ни от способа разбиения области  на части, ни от выбора точек в них, то он называется двойным интегралом от функции
на части, ни от выбора точек в них, то он называется двойным интегралом от функции 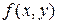 по области
по области  и обозначается
и обозначается 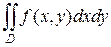 . В этом случае функция
. В этом случае функция 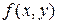 называется интегрируемой в области
называется интегрируемой в области  ;
;  – область интегрирования;
– область интегрирования; 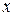 и
и 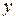 – переменные интегрирования.
– переменные интегрирования.
Таким образом, двойной интегралопределяется равенством
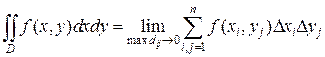 (2)
(2)
Здесь 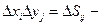 площадь элементарной области.
площадь элементарной области.
Перейдем от прямоугольной области к произвольной. Пусть  – замкнутая ограниченная область. Как и в рассмотренном выше случае, покроем эту область прямоугольной сеткой и построим интегральную сумму
– замкнутая ограниченная область. Как и в рассмотренном выше случае, покроем эту область прямоугольной сеткой и построим интегральную сумму 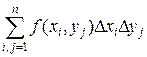 . Суммирование ведется по тем прямоугольникам, которые лежат внутри области и не имеют общих точек с границей. Если предположить, что граница области − спрямляемая кривая, то предельный переход при
. Суммирование ведется по тем прямоугольникам, которые лежат внутри области и не имеют общих точек с границей. Если предположить, что граница области − спрямляемая кривая, то предельный переход при 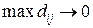 приведет к той же формуле (2).
приведет к той же формуле (2).
Для всякой ли функции 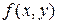 существует двойной интеграл? На этот вопрос отвечает теорема.
существует двойной интеграл? На этот вопрос отвечает теорема.
Теорема (достаточное условие интегрируемости функции).
Если функция 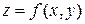 непрерывна в замкнутой области
непрерывна в замкнутой области  , то она интегрируема в этой области.
, то она интегрируема в этой области.
- Геометрический и физический смысл двойного интеграла
Рассмотрим две задачи, приводящие к двойному интегралу.
Объем цилиндрического тела
Пусть тело ограничено сверху поверхностью 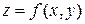
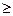 0, снизу — замкнутой областью
0, снизу — замкнутой областью  плоскости
плоскости 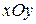 , с боков — цилиндрической поверхностью, образующая которой параллельна оси
, с боков — цилиндрической поверхностью, образующая которой параллельна оси 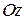 , а направляющей служит граница области
, а направляющей служит граница области  . Такое тело называется цилиндрическим (
. Такое тело называется цилиндрическим (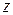 -цилиндрическим). Найдем его объем
-цилиндрическим). Найдем его объем 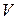 . Для этого разобьем область
. Для этого разобьем область  (проекция поверхности
(проекция поверхности 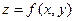 на плоскость
на плоскость 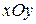 ) произвольным образом на
) произвольным образом на 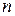 областей
областей 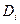 , площади которых равны
, площади которых равны 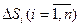 . Рассмотрим цилиндрические столбики с основаниями
. Рассмотрим цилиндрические столбики с основаниями 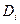 , ограниченные сверху кусками поверхности
, ограниченные сверху кусками поверхности 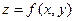 . В своей совокупности они составляют все тело. Обозначим объем столбика с основанием
. В своей совокупности они составляют все тело. Обозначим объем столбика с основанием 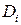 через
через 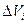 , тогда
, тогда
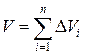
Возьмем на каждой площадке 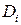 произвольную точку
произвольную точку 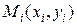 . Заменим каждый столбик цилиндром с тем же основанием
. Заменим каждый столбик цилиндром с тем же основанием 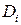 (площадь которого равна
(площадь которого равна 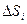 ), а в качествевысоты возьмем значение функции в точке
), а в качествевысоты возьмем значение функции в точке 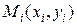 , то есть
, то есть 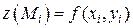 . Объем этого цилиндра приближенно равен объему
. Объем этого цилиндра приближенно равен объему 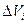 цилиндрического столбика, т. е.
цилиндрического столбика, т. е. 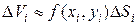 Тогда:
Тогда:
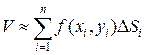 .
.
Это равенство тем точнее, чем больше число 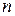 и чем меньше размеры «элементарных областей»
и чем меньше размеры «элементарных областей» 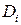 . Естественно принять предел этой суммы при условии, что число площадок
. Естественно принять предел этой суммы при условии, что число площадок 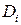 неограниченно увеличивается (
неограниченно увеличивается (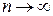 ), а каждая площадка стягивается в точку (
), а каждая площадка стягивается в точку (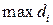
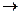 0), за объем
0), за объем 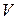 цилиндрического тела, то есть
цилиндрического тела, то есть
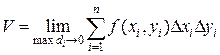 или
или 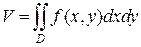
Итак, двойной интеграл от неотрицательной функции равен объему цилиндрического тела. В этом состоит геометрический смысл двойного интеграла.
Двойные интегралы
- Основные понятия и определения
Обобщением определенного интеграла на случай функций двух переменных является так называемый двойной интеграл.
Пусть в прямоугольной области 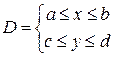 задана непрерывная функция
задана непрерывная функция 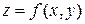 .Разобьем область
.Разобьем область  прямоугольной сеткой
прямоугольной сеткой
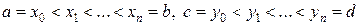
на «элементарные области» 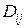 (
(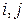 =
= 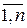 ), площади которых равны
), площади которых равны 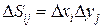 . Диаметром элементарной области
. Диаметром элементарной области 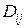 будем называть диагональ прямоугольника
будем называть диагональ прямоугольника 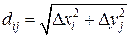 . В каждой такой области выберем произвольную точку
. В каждой такой области выберем произвольную точку 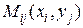 , умножим значение функции
, умножим значение функции 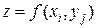 в этой точке на
в этой точке на 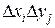 и составим сумму всех таких произведений:
и составим сумму всех таких произведений:
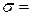
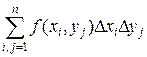 . (1)
. (1)
Эта сумма называется интегральной суммой функции 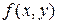 .Рассмотрим предел интегральной суммы (1), когда
.Рассмотрим предел интегральной суммы (1), когда 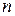 стремится к бесконечности таким образом, что
стремится к бесконечности таким образом, что 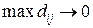 . Если этот предел существует и не зависит ни от способа разбиения области
. Если этот предел существует и не зависит ни от способа разбиения области  на части, ни от выбора точек в них, то он называется двойным интегралом от функции
на части, ни от выбора точек в них, то он называется двойным интегралом от функции 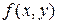 по области
по области  и обозначается
и обозначается 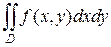 . В этом случае функция
. В этом случае функция 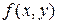 называется интегрируемой в области
называется интегрируемой в области  ;
;  – область интегрирования;
– область интегрирования; 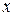 и
и 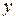 – переменные интегрирования.
– переменные интегрирования.
Таким образом, двойной интегралопределяется равенством
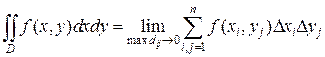 (2)
(2)
Здесь 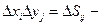 площадь элементарной области.
площадь элементарной области.
Перейдем от прямоугольной области к произвольной. Пусть  – замкнутая ограниченная область. Как и в рассмотренном выше случае, покроем эту область прямоугольной сеткой и построим интегральную сумму
– замкнутая ограниченная область. Как и в рассмотренном выше случае, покроем эту область прямоугольной сеткой и построим интегральную сумму 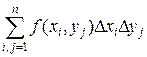 . Суммирование ведется по тем прямоугольникам, которые лежат внутри области и не имеют общих точек с границей. Если предположить, что граница области − спрямляемая кривая, то предельный переход при
. Суммирование ведется по тем прямоугольникам, которые лежат внутри области и не имеют общих точек с границей. Если предположить, что граница области − спрямляемая кривая, то предельный переход при 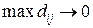 приведет к той же формуле (2).
приведет к той же формуле (2).
Для всякой ли функции 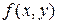 существует двойной интеграл? На этот вопрос отвечает теорема.
существует двойной интеграл? На этот вопрос отвечает теорема.
Теорема (достаточное условие интегрируемости функции).
Если функция 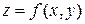 непрерывна в замкнутой области
непрерывна в замкнутой области  , то она интегрируема в этой области.
, то она интегрируема в этой области.
- Геометрический и физический смысл двойного интеграла
Рассмотрим две задачи, приводящие к двойному интегралу.
Объем цилиндрического тела
Пусть тело ограничено сверху поверхностью 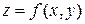
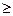 0, снизу — замкнутой областью
0, снизу — замкнутой областью  плоскости
плоскости 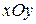 , с боков — цилиндрической поверхностью, образующая которой параллельна оси
, с боков — цилиндрической поверхностью, образующая которой параллельна оси 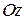 , а направляющей служит граница области
, а направляющей служит граница области  . Такое тело называется цилиндрическим (
. Такое тело называется цилиндрическим (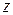 -цилиндрическим). Найдем его объем
-цилиндрическим). Найдем его объем 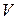 . Для этого разобьем область
. Для этого разобьем область  (проекция поверхности
(проекция поверхности 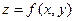 на плоскость
на плоскость 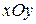 ) произвольным образом на
) произвольным образом на 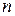 областей
областей 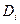 , площади которых равны
, площади которых равны 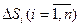 . Рассмотрим цилиндрические столбики с основаниями
. Рассмотрим цилиндрические столбики с основаниями 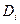 , ограниченные сверху кусками поверхности
, ограниченные сверху кусками поверхности 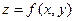 . В своей совокупности они составляют все тело. Обозначим объем столбика с основанием
. В своей совокупности они составляют все тело. Обозначим объем столбика с основанием 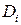 через
через 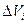 , тогда
, тогда
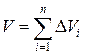
Возьмем на каждой площадке 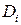 произвольную точку
произвольную точку 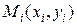 . Заменим каждый столбик цилиндром с тем же основанием
. Заменим каждый столбик цилиндром с тем же основанием 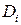 (площадь которого равна
(площадь которого равна 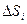 ), а в качествевысоты возьмем значение функции в точке
), а в качествевысоты возьмем значение функции в точке 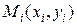 , то есть
, то есть 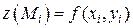 . Объем этого цилиндра приближенно равен объему
. Объем этого цилиндра приближенно равен объему 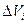 цилиндрического столбика, т. е.
цилиндрического столбика, т. е. 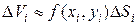 Тогда:
Тогда:
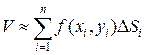 .
.
Это равенство тем точнее, чем больше число 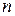 и чем меньше размеры «элементарных областей»
и чем меньше размеры «элементарных областей» 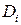 . Естественно принять предел этой суммы при условии, что число площадок
. Естественно принять предел этой суммы при условии, что число площадок 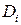 неограниченно увеличивается (
неограниченно увеличивается (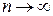 ), а каждая площадка стягивается в точку (
), а каждая площадка стягивается в точку (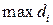
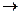 0), за объем
0), за объем 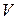 цилиндрического тела, то есть
цилиндрического тела, то есть
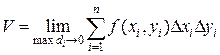 или
или 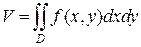
Итак, двойной интеграл от неотрицательной функции равен объему цилиндрического тела. В этом состоит геометрический смысл двойного интеграла.



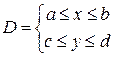 задана непрерывная функция
задана непрерывная функция 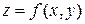 .Разобьем область
.Разобьем область  прямоугольной сеткой
прямоугольной сеткой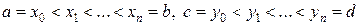
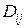 (
(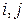 =
= 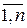 ), площади которых равны
), площади которых равны 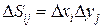 . Диаметром элементарной области
. Диаметром элементарной области 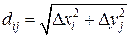 . В каждой такой области выберем произвольную точку
. В каждой такой области выберем произвольную точку 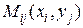 , умножим значение функции
, умножим значение функции 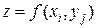 в этой точке на
в этой точке на 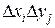 и составим сумму всех таких произведений:
и составим сумму всех таких произведений: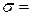
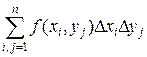 . (1)
. (1)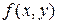 .Рассмотрим предел интегральной суммы (1), когда
.Рассмотрим предел интегральной суммы (1), когда 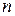 стремится к бесконечности таким образом, что
стремится к бесконечности таким образом, что 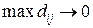 . Если этот предел существует и не зависит ни от способа разбиения области
. Если этот предел существует и не зависит ни от способа разбиения области 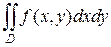 . В этом случае функция
. В этом случае функция 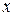 и
и 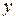 – переменные интегрирования.
– переменные интегрирования.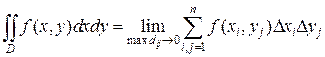 (2)
(2)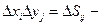 площадь элементарной области.
площадь элементарной области.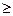 0, снизу — замкнутой областью
0, снизу — замкнутой областью 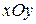 , с боков — цилиндрической поверхностью, образующая которой параллельна оси
, с боков — цилиндрической поверхностью, образующая которой параллельна оси 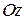 , а направляющей служит граница области
, а направляющей служит граница области 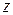 -цилиндрическим). Найдем его объем
-цилиндрическим). Найдем его объем 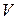 . Для этого разобьем область
. Для этого разобьем область 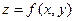 на плоскость
на плоскость 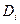 , площади которых равны
, площади которых равны 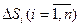 . Рассмотрим цилиндрические столбики с основаниями
. Рассмотрим цилиндрические столбики с основаниями 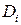 через
через 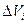 , тогда
, тогда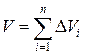
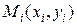 . Заменим каждый столбик цилиндром с тем же основанием
. Заменим каждый столбик цилиндром с тем же основанием 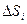 ), а в качествевысоты возьмем значение функции в точке
), а в качествевысоты возьмем значение функции в точке 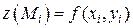 . Объем этого цилиндра приближенно равен объему
. Объем этого цилиндра приближенно равен объему 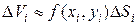 Тогда:
Тогда: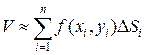 .
.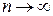 ), а каждая площадка стягивается в точку (
), а каждая площадка стягивается в точку (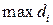
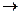 0), за объем
0), за объем 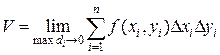 или
или