или Прошлое и будущее машинного обучения

__________________ TL;DR _____________________________________

В этой достаточно математически насыщенной главе будет дано краткое и по­верхностное введение в то, как сочетаются в современном машинном обучении нейронные сети и байесовский вывод. Мы:

• подробно разберем общий вид алгоритма ЕМ для обучения моделей со скры­тыми переменными;

• увидим на простых примерах основные идеи вариационных приближений;

• поговорим о конструкции вариационного автокодировщика, еще одной важ­ной порождающей модели с глубокими нейронными сетями;

• отметим, как байесовский вывод помогает построить новые формы дропаута;

• закончим книгу нашими размышлениями о том, куда все это катится и что ждет нас в будущем.

10.1. Теорема Байеса и нейронные сети

О святая математика, в общении с тобой хотел бы я про­вести остаток дней своих, забыв людскую злобу и неспра­ведливость Вседержителя.

Лотреамон

В главе 2 мы говорили о теореме Байеса и ее роли в машинном обучении, дол­го обсуждали пример с априорными и апостериорными распределениями броска монетки. А на протяжении всей книги не раз упоминали, что байесовский вывод в нейронных сетях тоже присутствует, и ссылались на какие-то загадочные вариа­ционные приближения, которые якобы делают возможным вывод в очень сложных моделях. В этой главе мы на простых примерах поймем, что это такое. Но сначала давайте ненадолго вернемся к самой теореме Байеса:

₌ ммщ ₌ мю®

* ' ’ P(D)                          f_ee_ep(D\0)p(J)d0-

В машинном 'обучении теорема Байеса позволяет из правдоподобия, которое обычно задается структурой модели, и априорного распределения, которое выра­жает наши представления об окружающем модель мире, получить апостериорное распределение, а затем, при желании, делать байесовские предсказания, интегри­руя по всем возможным значениям параметров в. С точки зрения нейронных сетей важно, что с помощью теоремы Байеса мы можем легко строить сложные вероят­ностные модели из простых, уточняя распределение скрытых параметров. Кроме того, выбирая априорное распределение, легко проводить регуляризацию. Более того, мы можем легко вводить модели с латентными (скрытыми) переменными и обучать их ЕМ-алгоритмом или вариационными методами, как мы увидим в этой главе. Задача байесовской оценки непрерывных скрытых переменных — это что-то вроде задачи понижения размерности: надо хорошо восстановить латентные пере­менные, и они станут важными признаками, кратко описывающими каждый объ­ект обучающей выборки.

Может показаться, что вся эта байесовская машинерия для нас не так уж важ­на, и можно обойтись максимальным правдоподобием. В главе 2 мы рассматрива­ли пример подбрасывания монетки: конечно, если бросков монетки один-два, без байесовских методов получится ерунда, но после тысячи бросков уже не так важно, каким было априорное распределение. А когда мы говорим о глубоких нейронных сетях, наборы данных исчисляются даже не тысячами, а миллионами и миллиар­дами — сколько пикселей в ImageNet? Однако проблема в том, что роль априор­ного распределения определяется не общим числом точек A^ata, а числом точек на каждый свободный параметр сети Ad[ata/A_model- И в реальности оказывается, что как только А^а1а увеличивается, мы тут же хотим подтянуть к ней и Amo deb чтобы сделать модель выразительнее. Сверточные сети, которые обучаются на ImageNet, могут иметь десятки миллионов параметров. Так что на самом деле машинное обу­чение все время находится в «зоне актуальности» байесовских методов.

На этом месте достаточно подготовленный читатель может подумать, что даль­ше мы будем говорить о том, как добавить в нейронную сеть априорные распре­деления и как сделать байесовский вывод в нейронной сети. Это действительно заслуживающая внимания тема, и мы к ней вернемся в разделе 10.5. Байесовский подход на самом деле может дать возможность не только получить веса в локаль­ном минимуме функции ошибки, но и оценить их дисперсию, а также и все апосте­риорное распределение p(w | D). Более того, в разделе 10.5 мы увидим, что такой подход дает совсем другой взгляд на дропаут, объяснив его с байесовской стороны.

Но по большей части далее мы будем говорить о совсем других вещах. Задача этой главы — постараться улучшить методы, использующиеся в байесовском выво­де, особенно вариационные приближения к сложным апостериорным распределе­ниям, с помощью «магии глубокого обучения». В качестве основных источников мы здесь рекомендуем исходную статью о байесовских автокодировщиках [280] и недавно появившееся подробное введение в тему [124].

Здесь появляется существенная разница в постановке задачи по сравнению со всем тем, что мы делали раньше. В машинном обучении модели часто имеют ве­роятностный смысл: мы обучаем не просто какую-то разделяющую поверхность, а распределение р(х), которое показывает, насколько, по мнению обученной мо­дели, вероятно появление той или иной точки в качестве точки данных. Уметь считать р(х) вполне достаточно для того, чтобы решать, например, задачу клас­сификации: чтобы распознавать рукописные цифры, мы обучаем десять моделей Рс,ръ • • • ,Р9> а потом для классификации просто сравниваем pq(xYpx(x), ..., pq ( x ): какая вероятность больше, ту цифру мы и выдадим в качестве ответа.

А в разделе 8.2 мы говорили о том, что часто хочется не просто распознавать уже взятые откуда-то объекты, но и создавать их самостоятельно. Например, мы бы хотели научиться не только распознавать рукописные цифры на основе датасе­та MNIST, но и самостоятельно их генерировать, «писать от руки». Или генериро­вать картины в узнаваемом стиле известного художника, как в сервисах DeepArt и Prisma. Или... но здесь оставим читателю место, чтобы он мог дать волю соб­ственной фантазии. Для этого нужно научиться не просто вычислять распределе­ние р(х), а сэмплировать из него, порождать точки по распределению р(х).

Эта задача решалась, конечно, и в классическом байесовском обучении: есть, например, большая область методов Монте-Карло на основе марковских цепей (Markov chain Monte-Carlo), которые предназначены как раз для того, чтобы на­учиться сэмплировать из распределений, которые мы умеем только вычислять. Мы сейчас не будем углубляться в эту тему и отошлем читателя к соответствующим учебникам [44, 343, 381], а сами только скажем, что эти методы для очень слож­ных распределений (таких, как, например, распределение человеческих лиц в про­странстве фотографий) работают крайне медленно или не работают вовсе.

В этой главе мы будем обучать модель сэмплировать (порождать точки) из сложного распределения с помощью нейронных сетей, которые будут здесь иг­рать роль черного ящика для приближения какой угодно функции — в данном слу­чае как раз плотности нужного распределения. Точнее говоря, нейронные сети бу­дут обучаться преобразовывать. какое-нибудь простое распределение, обычно нор­мальное со. стандартными параметрами, в то, которое нам нужно. Если кратко опи­сать предстоящую главу с математической точки зрения, мы рассмотрим способ строить приближения к сложным распределениям, в котором приближение берет­ся из некоторого класса функций, а потом начнем в качестве этого класса функ­ций подставлять нейронные сети. В результате получатся очень хорошо идейно мотивированные модели, которые многим исследователям представляются буду­щим глубокого обучения.

Сразу предупредим, что легко не будет — это, наверное, самая математически плотная глава во всей книге. С одной стороны, при первом чтении остаток главы, наверное, можно пропустить, да и на практике никто вас пока что не заставит при­менять именно эти методы. Но с другой стороны, эту главу можно считать своеоб­разной лакмусовой бумажкой: если вы можете ее прочесть и понять, у вас не долж­но возникнуть проблем с тем, чтобы читать самые современные статьи о глубоком обучении, и основную цель, которую мы ставим в этой книге, можно будет считать достигнутой. Итак, в путь!    *

10.2. Алгоритм ЕМ

Бедный Карлсон! Ему не позавидуешь. Алгоритм заставит его съесть пятьсот плюшек. Все до единой! И он наверняка умрет от обжорства.

В. Паронджааов. Дружелюбные алгоритмы, понятные каждому

Чтобы применить байесовские методы к нейронным сетям (точнее, как мы увидим ниже, наоборот — нейронные сети к байесовским методам), сначала придется разо­браться в том, как эти самые байесовские методы вообще работают. Мы начнем с того, что дадим байесовское обоснование одного из главных методов классиче­ского обучения без учителя, алгоритма Expectation-Maximization, который обычно называют просто ЕМ-алгоритмом.

Идея ЕМ-алгоритма довольно проста. Представьте себе, к примеру, задачу кла­стеризации на обычной плоскости R2: у вас есть набор точек, и вы хотите разбить их на подмножества так, чтобы внутри каждого из них точки были «похожи» друг на друга, то есть находились бы близко друг от друга, а точки из разных подмно­жеств как можно более существенно различались бы, то есть были бы далеки на плоскости.

Задачу кластеризации, конечно, можно решать очень многими разными спосо­бами [5,573], и ЕМ не всегда будет лучшим (как минимум он довольно медленный по сравнению с другими), но этот метод применим и к массе других задач,,а кла­стеризация — хороший способ его проиллюстрировать.

Чтобы применить ЕМ к кластеризации, нужно представить себе все данные о решении задачи кластеризации, которые могли бы у нас быть. В полном набо­ре данных у каждой точки будет написано, какие у нее координаты (это мы знали и раньше) и какому кластеру она должна принадлежать — а вот это как раз та ин­формация, которую мы должны получить. В этом представлении один тестовый пример — это пара           где zt показывает, какому кластеру принадлежит эта

точка, и мы не знаем значений Z{.

Заметьте разницу: в «обычной» модели тоже всегда есть веса или параметры, которые мы пытаемся обучать, но их, как правило, относительно мало, меньше, чем данных, а тут мы видим, что на каждую точку в данных приходится целая своя переменная. Именно в таких ситуациях, когда в имеющихся данных некото­рые переменные нам известны, а некоторые отсутствуют, и пригождается обычно ЕМ-алгоритм.

Далее, чтобы применить ЕМ-алгоритм, нужно сделать какие-то вероятностные предположения о том, как были порождены эти самые данные со скрытыми пере­менными. В случае кластеризации, проще говоря, нужно сделать предположения о форме кластеров. Давайте рассмотрим самый простой случай, когда точки лежат даже не на плоскости, а на прямой, и мы предполагаем, что они порождены двумя кластерами в виде нормальных распределений; более того, давайте предполагать, что дисперсия у этих распределений одинакова и равна а: ~ Ы[х \; р>,сг²) в пер­вом кластере, Х2 ~ М{х 2; дь<т²) во втором кластере.

А это значит, что распределение точек из обоих кластеров вместе представляет собой смесь двух нормальных распределений:

х ~ аЯ(х; m i#² ) 4- (1 - а)ЛГ(х; Л2,&²),

где а показывает сравнительный вес кластеров друг относительно друга, то, на­сколько больше точек попадает в один кластер, чем в другой. То есть, математи­чески говоря, наша задача состоит в том, чтобы найти параметры максимального правдоподобия (а, дь №2) У этой смеси распределений.

Заметьте, что никаких скрытых переменных г пока что в модели нет. И мы сей­час можем записать эту задачу поиска параметров максимального правдоподобия в виде обычной задачи оптимизации:

N

a,Mi> A2 = arg                             х^цсС) + (1 - а)Л/(хц Ц2,а² где si,.. ,х^ — это точки из имеющегося набора данных.

Проблема здесь состоит в том, что эта функция слишком сложна; посмотри­те — это огромное произведение сумм, и если раскрыть в нем скобки, слагаемых будет экспоненциально много. А если перейти к логарифмам, то мы получим боль­шую сумму логарифмов сумм, что тоже не очень помогает. Как все это оптимизи­ровать — непонятно.

Но если бы мы знали, какая точка из какого кластера была взята, С\ или С2, то легко подсчитали бы параметры максимального правдоподобия. Мы тогда просто разделили бы точки по соответствующим кластерам, и оценили среднее нормаль­ного распределения в каждом и долю каждого кластера:

 

Или формально — давайте введем переменную которая равна нулю, если точ­ка была взята из С\, и единице, если из С2. Тогда наш вероятностный процесс, по­рождающий точки, становится двухступенчатым, разбивается на две независимые части^[97]: сначала мы случайно выбираем переменные zi с вероятностью а, то есть общим правдоподобием:

N

p(Z | а) = JJ a^Zi(i — a)¹ ~Z,

i =1

а потом с уже известными Z{ набрасываем точки из соответствующих кластеров:

N

i =1

Иначе говоря, мы теперь решаем такую задачу оптимизации (давайте для удобства сразу перейдем к логарифмам):

N

а = arg max   fa In а + (1 - zA In (1 - а)),

а

i=1

£2 (bPfa/W ^[98] ) + (1 - Zi')p(x;p2,cA, l=l

гдер(х;р,а) — плотность нормального распределения, р(х; /х,сг) =                               •

Обратите внимание, что теперь эта задача оптимизации распадается на три со­вершенно независимые и по отдельности довольно простые задачи:

• найти а как arg max_Q Y a L i ( ha -h (1 - zi) In (1 - a)); это всего лишь по­

иск параметра максимального правдоподобия для подбрасывания монетки, и найти оптимальное а легко: а =                                                                              = 1^1;

• найти р\ как arg max_M1 J2iz=i Р         М1>^²) (обратите внимание, что в сумме

только те слагаемые, для которых Zi = 1, зависят от pi, и — чудесное совпаде­ние — они-то как раз и не зависят от даХэто всего лишь поиск параметра мак­симального правдоподобия для нормального распределения, и тут тоже р ц легко найти просто как среднее точек в первом кластере: fa. =      YJx^^Ci

• и, аналогично, зависящие от Ц2 слагаемые теперь не содержат /21, мы решаем

задачу arg max_M1М2,ст²) и находим д =                                 Е®г?С₂ ^хг

На данный момент у нас получилось, что если zi известны, то задача сразу раз­бивается на простые подзадачи и решается легко и непринужденно. Но что делать в реальной ситуации, когда Z{ неизвестны?

Идея алгоритма ЕМ состоит в том, чтобы притвориться, будто бы мы знаем z^ а затем попеременно уточнять то скрытые переменные, то параметры модели. ЕМ означает Expectation-Maximization, и в полном соответствии с названием алгоритм ЕМ повторяет в цикле два шага:                                              *

•
Е-гиаг: для известных параметров модели a^/xi,/Х подсчитать ожидания скры­тых переменных z% для кластеризации мы этого еще не делали, но это тоже несложно — если все параметры известны, то чтобы подсчитать, с какой веро­ятностью точка принадлежит тому или иному кластеру, нужно просто найти плотности распределений одного и другого кластера в этой точке:

p(x = Xi I |/z = щ) + p(x = Xi ||д =                          '

e-

• М-гиаг: зафиксировать Zj — E [;zi] и пересчитать параметры модели по уже известным формулам:

_Xi eCi

Получился итеративный алгоритм, который сначала инициализирует парамет­ры модели случайными значениями (в случае кластеризации разумно выбрать две случайные точки из данных и объявить их центрами кластеров), а затем постепен­но уточняет и параметры, и оценки скрытых переменных, пока не сойдется.

Итак, мы поняли, как работает ЕМ-алгоритм, на примере задачи кластериза­ции. Мы получили некий метод, который выглядит разумно и дает хорошие ре­зультаты (по крайней мере на этой задаче), но звучит он пока что довольно по­дозрительно: с какой стати такое «вытягивание самого себя за уши» из случай­ных значений латентных переменных или параметров модели должно приводить к успеху? Давайте теперь разберемся не только в том, как работает ЕМ в общем виде, но и почему он работает.

Для этого придется перейти к той самой обещанной «сложной математике». Сейчас мы дадим формальное обоснование алгоритма ЕМ в общем виде; формул будет много, и для читателя, который раньше их не видел, у нас есть такой совет: по­старайтесь «протащить» через эти формулы интуицию из примера, который мы не случайно так подробно рассмотрели. Пример с кластеризацией (то есть со смесью нормальных распределений) достаточно полно отражает все особенности задачи, и на нем можно понять и то, что происходит ниже.

Как и в примере с кластеризацией, мы будем решать задачу поиска парамет­ров максимального правдоподобия в по данным X = { х...,ждг}; правдоподобие можно записать так:

Ы Р \хэ = р(*\0) = П |К^\в),

ч

а максимизировать, понятное дело, можно не само правдоподобие, а его логарифм £(в | X) = logL(0 | X), ЕМ может помочь, если этот максимум трудно найти аналитически.

Давайте предположим, что в данных есть латентные переменные (скрытые пе­ременные, скрытые компоненты), причем модель устроена так, что если бы мы их знали, задача стала бы проще, а то и допускала бы аналитическое решение. На са­мом деле, совершенно не обязательно, чтобы эти переменные имели какой-то фи­зический смысл, может быть, так просто удобнее, но физический смысл (такой, как номер кластера в предыдущем примере), конечно, обычно помогает их придумать. Например, представьте себе задачу порождения картинок с изображением цифр (мы рассмотрим этот пример в разделе 10.4). В этой задаче нам нужно породить всю картинку целиком так, чтобы она была «посвящена» одной и той же цифре, ведь половинка двойки плюс половинка восьмерки дадут скорее что-то похожее на рукописный твердый знак, чем на конкретную цифру. И это удобнее всего выра­зить именно так: сначала мы порождаем скрытую переменную г, которая соответ­ствует тому, какую цифру хочется породить, а потом все распределение видимых данных р(х | z) будет уже зависеть от значения z [124].

В любом случае совместная плотность набора данных У = (X,Z) такова:

Р(У I в) = p(x,z | 0) = p{z | х,0)р(х | 0),

и полное правдоподобие данных теперь составляет Ь(в | Z) = р(Х,У \ в).

Это случайная величина (потому что У неизвестно), а настоящее правдоподо­бие можно вычислить как ожидание полного правдоподобия по скрытым перемен­ным У:

ЬО=ЕурХУ\0)1Хв]-

Теперь Е-шаг алгоритма ЕМ вычисляет условное ожидание (логарифма) пол­ного правдоподобия при условии X и текущих оценок параметров в_п:

Q(0,0n)=E\logp(X,yi0)IX,O_n].

Здесь вп — текущие оценки параметров модели, а 0 — неизвестные значения, которые мы хотим получить в конечном счете; это значит, что <2(0, в_п) — это функ­ция от 0. Условное ожидание можно переписать так:

Е [\о%р(Х,У | в) | Х,вп] = J log p(X,z | в)р(г | X,0n)dz,

где p(z | Хвп) — маргинальное распределение скрытых компонентов данных.

ЕМ лучше всего применять, когда это выражение легко подсчитать, может быть, даже можно подсчитать аналитически. Вместо p(z | Х0п) можно подставить p(z,X | вп) = p(z | Х,вп)р(Х | вп), от этого ничего не изменится.

В итоге после Е-шага алгоритма ЕМ мы получаем функцию Q(0, вп). А на М-шаге максимизируем функцию <2 по параметрам модели, получая новую оцен­ку 0п+1:

0n+i = arg max<2(0,0_n).

и

Затем эта процедура повторяется до сходимости.

Осталось понять, что же, собственно, означает эта таинственная функция Q(0, 0п) и почему все это работает.

Мы хотели перейти от вп к 0, для которого £(в) > £(вп). Давайте оценим раз­ность этих двух величин. Дальше мы будем вести достаточно длинную цепочку равенств, которые будем по ходу комментировать:

=...

(по определению и одной из предыдущих формул)

... = log (у р{Х I z,0)p(z I 0)dz) - log р(Х I вп) =...

(домножим и разделим на p(z | Х,впУ)

■ •■=*(//* I                                                            ¹ «^г ■

Рис. 10.1. Алгоритмы миноризации-максимизации

(по неравенству Йенсена: логарифм — выпуклая функция, а математическое ожи­дание — линейное преобразование, так что \ogEpX)f (х) > Е_р(_ж) log f (х), а у нас берется ожидание по распределению p(z | A",0n))

(занесем теперь р{Х | в_п) под интеграл и под логарифм — в нем z не участвует, так что для математического ожидания по z это просто константа)

 

Итак, мы получили, что

 

Кроме того, легко доказать, что 1(0пвп) = Иначе говоря, мы нашли ниж­

нюю оценку для функции £(6), которая касается, оказывается равной £(в) в точ­ке в_п. Это значит, что в рамках ЕМ-алгоритма мы сначала нашли нижнюю оценку для функции правдоподобия, которая касается самого правдоподобия в текущей точке, а потом сместились туда, где она максимальна; естественно, при этом сама функция правдоподобия тоже увеличится, ей просто деваться некуда (рис. 10.1). Такая общая схема оптимизации, при которой максимизируют нижнюю оценку на оптимизируемую функцию, иногда еще называется ММ-алгоритмом, от слов Minorization- Maximization.

Осталось только понять, что максимизировать можно Q. И снова придется вы­терпеть цепочку равенств:

0_n+1 = arg max/(0,0_n) =...

0

(перепишем по формуле выше)

... arg max {«(»„) ₊               |         log                                            <*} = '''

(выбросим из-под arg max все, что не зависит от в — от этого точка, где достигается максимум, не изменится)

... arg max fj p(z | X,0n) log (p(X | z,0)p(z | 0))dz| =...

(свернем опять произведение p(x | z)p(z) в совместную вероятность p(x,z))

=... arg max 1У p(zl X,0_n) \ogp(X,z I 0)d* j = arg max {Q(0,0n)} •

Вот и получился ЕМ-алгоритм.

Заметим, что для того, чтобы ЕМ-алгоритм сработал, в принципе достаточно просто находить 0n+i, для которого <?(0п+ь вп) > Q(6n, Bn)i чтобы £(в) увеличи­валось, не обязательно находить именно максимум ее нижней оценки, достаточно сместиться туда, где нижняя оценка просто хоть на сколько-нибудь увеличится. Такая схема называется обобщенным ЕМ-алгоритмом (Generalized ЕМ).

10.3. Вариационные приближения

Бах решил, что тут, пожалуй, лучше всего подойдут вариации, хотя до сих пор считал, что это дело неблагодарное... Тем не менее, эти ва­риации, как и все, что он создавал в то время, получились у него вели­колепными... Граф называл этот цикл своими вариациями. Он никак не мог ими насладиться, и долго еще, как только у него начиналась бессонница, он, бывало, говорил: «Любезный Гольдберг, сыграй-ка мне какую-нибудь из моих вариаций».

И. Форкель. О жизни, искусстве и о произведениях Иоганна Себастьяна Баха

Следующая важная идея байесовского вывода, которую нам нужно осознать и для которой, собственно, и предназначены описанные в этой главе методы, — это вари­ационные приближения. Их рассмотрение будет очень похоже на то, что мы говори­ли о ЕМ-алгоритме, и мы сможем еще раз обсудить всю эту ситуацию со скрытыми параметрами с немножко другого угла зрения.

Мы по-прежнему находимся в той же общей ситуации, что и в предыдущем раз­деле, где нам помогал ЕМ-алгоритм: предположим, что набор данных X = был порожден двухступенчатым процессом с параметрами модели в: сначала из
какого-то ' априорного распределения p(z | в) породили вектор скрытых перемен­ных z, а затем из условного распределения р(х | zQ) породили собственно точку х. Мы знаем распределения p(z | в) и р(х | z,d), но распределение р(х | в):

р(х | в) = J р(х | z,0)p(z | 0)dz

для нас слишком сложное, мы не можем его подсчитать напрямую.

ЕМ-алгоритм применялся в ситуациях, когда мы можем либо аналитически, либо численно подсчитать распределение скрытых переменных при фиксирован­ных параметрах p(z | ж, в); обычно его можно подсчитать по теореме Байеса:

р(х I z,0)p(z I 0)
р(«| 0)

Тогда мы считаем это распределение на Е-шаге ЕМ-алгоритма, получаем оцен­ки ожиданий z, максимизируем целевую функцию на М-шаге по в с фиксирован­ными оценками и так далее, как в предыдущем разделе.

Но что если даже распределение p(z | х, в) подсчитать не получается? Это не такой уж редкий случай: представим себе, например, что распределение р(х | z,0) задано привычной нам нейронной сетью. Даже обычная двухслойная нейронная сеть с нелинейным скрытым уровнем — это настолько сложное распределение, что просто взять и умножить его на априорное распределение p{z | в) не получится.

В математическом моделировании есть универсальный ответ на все подобные затруднения: если структура объекта слишком сложна, значит, нужно просто при­близить его с помощью какого-нибудь более простого объекта. Суть вариационно­го метода при этом состоит в том, что более простое приближение мы ищем среди некоторого класса функций (распределений), и пытаемся найти в этом более про­стом классе элемент, который наиболее похож на тот «сложный» элемент, который мы приближаем. Если этот класс будет задан параметрически, значит, у нас по­явятся новые вариационные параметры, по которым мы, будем надеяться, сможем оптимизировать приближение. Впрочем, одна из ключевых особенностей метода, который мы сейчас рассматриваем, как раз в том, что приближение мы ищем вовсе не параметрически.

Однако в целом смысл происходящего точно такой же: мы приближаем слож­ное распределение более простой формой, выбирая то распределение из более про­стого семейства, которое лучше всего приближает сложное распределение. «Похо­жесть» можно определить по расстоянию Кульбака — Лейблера:

Чтобы объяснить, как все это работает в реальности, вернемся сначала к од­ному из взглядов, на ЕМ-алгоритм: пусть X — наблюдаемые переменные, a Z — латентные. ЕМ-алгоритм предполагает, что мы умеем считать плотность совмест­ного распределения р(Х, Z | в), а хотим максимизировать р(Х | в). Они связаны, например, так:

p(X,Z\e)=p(X\OPp(Z\Xf),

а значит,

In р(Х | в) = lnp(X, Z | в) - In p(Z | Xfi).

Рассмотрим новое распределение q(Z), которое и будет служить тем самым приближением. Давайте просто механически добавим его в наши формулы. Рас­смотрим формулу выше и возьмем в ее левой и правой частях ожидание по рас­пределению q(Z):

j q(Z)\np(X | 0)dZ = f q(Z)\np(X,Z \ 9)dZ - f q{Z) lnp{Z \ X,0)dZ.

«Z                                      J Z                                         j z

Ho In p(X | 0) от Z не зависит, так что ожидание слева равно самому In р(Х \ в):

I np C X^^ [ q(Z)lnp(X,Z\0)dZ- [ q(Z)\np(Z \ X,e)dz.

Jz                                           Jz

А теперь справа давайте под интегралом добавим и вычтем q(Z) In q(Z) (да, это выглядит как непонятная магия — спокойствие, сейчас все прояснится); в резуль­тате у нас получится:

lnp(X|0) = J q(Z) (1пр(Х, Z \ в) - l n q(Z)+ln q(Z)-\np(Z\X,&))dZ

= £(q,e) + KLqpziX,*)),

raeC(q,e) =                                           — некий функционал уже от p(X,Z \ 0> от сов­

местного распределения, которое, по нашему предположению, достаточно простое.

Посмотрите, что у нас получилось: KL(q\|p(Z | X, в)) — это расстояние Куль­бака — Лейблера; оно всегда неотрицательно, и равно нулю только если q = р. По­этому C(q, в) — это нижняя оценка на 1п р(Х \ в). И в ЕМ-алгоритме, получается, мы для текущего в п:

• на Е-шаге максимизируем C(q, 0п) по q для фиксированного 0п\ максимум достигается, когда KL(q\|p(Z | X, в)) = 0, то есть когда q(Z) = p(Z \ X, вп);

• на М-шаге фиксируем q{Z) и максимизируем нижнюю оценку правдоподо­бия £(д, в) по в, получая 0n+i-

Нижняя оценка £(д, в) — это один из важнейших объектов в теории вариаци­онных приближений. Она называется вариационной нижней оценкой (variational

lower bound, evidence lower bound, ELBO). А сами вариационные методы рабо­тают так: пусть мы хотим максимизировать р(Х) со скрытыми переменными Z, и p(Z | X) — сложное распределение. Давайте искать приближение к нему в виде распределения более простой структуры q(Z). Тогда по тем же соображениям

1п р(Х) = C(q) + KL(q||p(Z | X)), где

C(q) = j q(Z) 1n                            KL(g||p) = - f q(Z) 1n ^P^_q^ dZ.

И мы снова можем максимизировать вариационную нижнюю оценку C(q), при­ближая q(Z) Kp(Z | X). Здесь получился редкий частный случай функциональ­ной оптимизации: казалось бы, нам нужно было решить нереально сложную зада­чу, максимизировать £(д, вП) по функции, по распределению q. Но в результате нехитрых преобразований оказалось, что для этого достаточно всего лишь подсчи­тать q(Z) = p(Z | X, в п), или хотя бы приблизить q(Z) «p(Z | X, 0_П). Если бы мы брали q(Z) из параметрического семейства, то поиск q(Z) свелся бы к (возможно, приближенному) решению некоторой задачи оптимизации, но прелесть вариаци­онных приближений в том, что часто параметрическое семейство и вовсе не нужно!

Рассмотрим сначала главный частный случай вариационных приближений — случай, когда q полностью факторизуется, раскладывается на множители, завися­щие от одной переменной или непересекающихся подмножеств переменных:

м

q(Z) = ]TJ qi(Zi), Zi A Zj = 9 для всех i,j.

i=l

Ключевой момент здесь в том, что мы никак не ограничиваем q \! Никаких пред­положений о форме распределений, никакого параметрического семейства. Одна­ко теперь мы просто должны максимизировать C(q), сделав предположение о фор­ме q(Z\. q(Z) = P[f£i qi(Zi)' Оставим то, что зависит от одного фактора q^

 

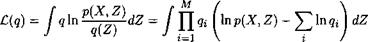
— / Qj f 1 nP(X, Z) JQ qidZi dZj - f qj 1n qjdZj + const =

L                         J

— f qj lnp(X, Zj)dZj — f qj 1n qjdZj + const,

где lnp(X, Zj) = Ey [lnp(X, Z)] + const.

Как теперь максимизировать такую величину:

qj lnp(X, Zj)dZj - У qj InqjdZ j + const

no qj при фиксированных qi,i Ф jl Эта формула - просто KL-расстояние между

qj(Zj) и р(Х, Zj)l Значит, можно брать q * так, чтобы:

In q*(Zj) = Etyj [In p(X, Z)l + const,

а эта задача обычно решается достаточно просто.

Давайте разберем конкретный пример: приблизим двумерное нормальное рас­пределение произведением одномерных. Рассмотрим двумерный гауссиан:

Л=(>п

Это распределение не раскладывается на независимые множители, но давайте приблизим его распределением, которое раскладывается: q(zf = qi(zi)q2(z2).

Воспользуемся выведенной выше формулой In q*(Zj) = E/j [lnp(X, Z)l 4- +const; когда мы подсчитываем qi(zi), в const попадает все, что не зависит от z^:

 

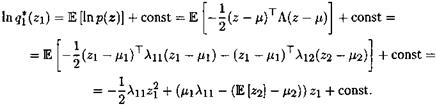
Смотрите — в качестве приближения у нас получилось нормальное распределе­ние, причем получилось само по себе, без нашего участия! Выделяя полный квад­рат:

9*(*1) =Af(zi | n^i,Af₁¹), где mi = щ - А[/А12(Е [z₂| - т)-

Аналогично,

/2(22) = M(z2 | m2, A^^i), где m2 = М2 - А-^А^Е [zi] - mi).

Здесь Е [zi| = mi, Е [22] = m2, и нам надо просто решить систему; получится, естественно, mi = щ, m2 = /2-

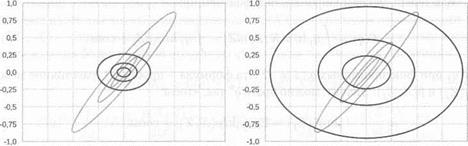
-1,0 -0,75 -0,5 -0,25  0,0  0,25  0,5   0,75  1,0          -1,0  -0,75 -0,5 -0,25  0,0   0,25  0,5  0,75   1,0

а                                                                          б

Рис. 10.2. Вариационные приближения к двумерному гауссиану

 

Сравним теперь это с обычным маргиналом (проекцией): на рис. 10.2, а мы изобразили полученное вариационное приближение, а на рис. 10.2, б — произведе­ние проекций на оси X и Y. Мы видим здесь тот самый эффект, который мы обсуж­дали в разделе 8.5 (вспомните рис. 8.11) для разных вариантов расстояния Куль­бака — Лейблера: в то время как произведение маргиналов дает широкое «накры­вающее» распределение, вариационные приближения выбирают один конкретный пик, что для задач машинного обучения обычно предпочтительнее.

А важный для нашего дальнейшего рассмотрения конкретный пример — это метод главных компонент (principal components analysis, РСА). Это простейшая модель с непрерывными латентными переменными; возможно, вы слышали о ней в «обычных» курсах статистики или машинного обучения. Смысл РСА состоит в том, чтобы сократить размерность, потеряв как можно меньше информации о да- тасете; формально это значит, что мы пытаемся найти такое подпространство мень­шей • размерности, проекция на которую сохраняет как можно большую часть дис­персии исходного набора точек. Алгоритмически обычный РСА сводится к диаго­нализации эмпирической ковариационной матрицы датасета, то есть к подсчету ее собственных векторов.

Но сейчас нас интересует байесовский взгляд на то, что происходит в методе главных компонент. Итак, пусть наши исходные объекты находятся в пространстве размерности Д, а латентные переменные — в пространстве размерности d: X е R^D, Z е Rd. Запишем распределения:

т                       т

p(X,Z \0) =                       | в) == ]~[р(.т:* | ъ6)р(& | в).

i=1                      г=1

Будем предполагать, что латентные переменные z] берутся из нормального рас­пределения вокруг нуля, а собственно наблюдаемые переменные получаются из них линейным преобразованием с нормально распределенным шумом:

т

p(X,Z | «> = П"(%i\f + Wzi,aI)A/'(zi \ 0,I). i= 1

Здесь матрица W размерности Dxd и вектор /х е — это и ессь искомые веса. Задача та же: максимизировать р(Х \ в) по в. Ее можно, конечно, решить явно, как в исходном методе главных компонент, а можно и ЕМ-алгоритмом: на Е-шаге искать p(zi | х*,0), а на М-шаге максимизировать Ez log p{X,Z | в); в этом простом частном случае и Е-, и М-шаг можно выразить явно! аналитически.

Казалось бы, странно: зачем запускать итеративный процесс, если можно про­сто явно все посчитать через собственные векторы? Оказывается, что иногда так действительно лучше: сложность метода главных компонент в явном виде состав­ляет O(nD ² f D 3) (искать собственные векторы у больших матриц недешево!), а сложность одной итерации ЕМ-алгор<