Глава II. Волны
§ 2.1. Упругие волны
 Колебания, возбуждаемые в какой-либо области пространства, могут передаваться соседним областям, удаляясь от источника. Такой процесс распространения колебаний называется волной. Область пространства, занятую волной, называют волновым полем. Все точки волнового поля колеблются согласованно друг с другом. Волновое поле может увеличиваться в размерах и перемещаться в пространстве. Это явление широко распространено в природе и технике: достаточно вспомнить, что звук - упругие, а свет - электромагнитные волны.
Колебания, возбуждаемые в какой-либо области пространства, могут передаваться соседним областям, удаляясь от источника. Такой процесс распространения колебаний называется волной. Область пространства, занятую волной, называют волновым полем. Все точки волнового поля колеблются согласованно друг с другом. Волновое поле может увеличиваться в размерах и перемещаться в пространстве. Это явление широко распространено в природе и технике: достаточно вспомнить, что звук - упругие, а свет - электромагнитные волны.
Рассмотрим процесс распространения колебаний в упругом стержне, по торцу которого бьют молотком (рис. 2.1). Будем считать стержень достаточно длинным, теоретически бесконечно длинным. В момент удара деформируется, а именно, сжимается только ближайший к торцу элемент объема стержня. Возникшая в нем упругая сила стремится вернуть этот объем в исходное положение, при этом левое сечение рассматриваемого объема движется влево, правое - вправо. Смещение правого сечения сжимает прилегающий к нему следующий элемент объема, который упруго деформируется, создавая возвращающую силу, растягивающую сжатый объем. В результате вдоль стержня распространяются процессы сжатия и растяжения, сопровождающиеся колебаниями его точек вдоль оси l.. Мысленно выделим малый объем стержня D V=S D l, заключенный между сечениями 1 и 2, где S- площадь сечения стержня (рис. 2.2). При деформации сечение 1 сместится на величину x 1, сечение 2 - на величину- x 2, при этом возникнут упругие силы F1 и F2, так что уравнение движения (второй закон Ньютона) рассматриваемого объема D V примет вид: F2 - F1 = r D Va, где r - плотность материала стержня, a - ускорение. Поделив обе части уравнения движения на площадь стержня S и учитывая, что нормальное напряжение s = F/S, получим:
 s 2 - s 1 = r a D x (2.1)
s 2 - s 1 = r a D x (2.1)
Согласно закону Гука s =E e, где E - модуль Юнга, e -деформация, т.е. относительное удлинение. В исходном состоянии рассматриваемый нами участок стержня имел длину D l. При распространении колебаний вследствие различия смещений сечений 1 и 2 его удлинение составило величину D x = x 2 - x 1, соответственно относительное удлинение - D x./ D l. При D l ®0 относительное удлинение называется деформацией e =d x /d l;деформации e 1 =(d x /dx)1 и e 2 =(d x /dx)2 в сечениях 1 и 2соответственно могут различаться. C учетом рассмотренного, уравнение (2.1) примет вид:
E ((d x / dx)2 - (d x / dx)1)= E D (d x / dl) = r a D l (2.2)
Учитывая, что ускорение a= d2 x /dt2 при малых D l примерно одинаково для всех точек рассматриваемого малого объема D V, а также преобразовав изменение деформации следующим образом: (d x /dx)2 - (d x /dx)1= D (d x /dx)= (d2 x /dx2) D x, получим уравнение движения в виде:
E(d2 x /d l 2)= r (d2 x /dt2) (2.3)
Найдем решение этого уравнения, исходя из физических соображений. Пусть левый торец стержня (l = 0), изображенного на рис.2.1, колеблется по закону x (0,t)=Asin w t и является источником колебаний.Распространяясь со скоростью u, эти колебания достигнут сечения стержня с координатой l спустя время t = l / u, так что закон движения этих точек имеет вид:
x (x,t)=Asin w (t- t)= Asin w (t-l/ u) (2.4)
Прямой подстановкой убеждаемся, что (2.4) является решением (2.3) при условии, что
u =  (2.5)
(2.5)
Из вывода формулы (2.4) следует, что u имеет смысл скорости распространения фазы и называется фазовой скоростью. Используя (2.5), перепишем уравнение (2.3) в виде:
d2 x /d l 2 = (1 / u 2)(d2 x /dt 2) (2.6)
Уравнение (2.6) называется волновым уравнением. Запомним, если какой-либо физический процесс описывается уравнением, где частная производная второго порядка по координате пропорциональна частной производной второго порядка по времени, то это волновой процесс, то-есть процесс распространения колебаний с фазовой скоростью, определяющейся коэффициентом пропорциональности между этими частными производными. Позднее мы еще не раз встретимся с волновым уравнением.
Направление распространения волны (ось l) называется лучом. Уравнение (2.4) описывает закон колебаний разных точек луча, причем все точки колеблются с одинаковой частотой w, одинаковой амплитудой A и собственной фазой j = w (t- l / u), величина которой зависит от времени t и расстояния l точки от источника колебаний. Точки, колеблющиеся в одинаковой фазе, образуют поверхность, называемую волновой. “Передовая” волновая поверхность, отделяющая волновое поле от невозмущенной области пространства, называется фронтом волны. В нашем случае волновые поверхности и фронт волны имеют вид плоскостей l =const, поэтому формула (2.4) называется уравнением плоской бегущей волны или луча. Источником плоской волны является гармонически колеблющаяся плоскость - левый конец стержня (рис. 2.1). Если источником колебания в однородной изотропной среде является точка, то по аналогии с (2.4) получим:
x (r,t)=Asin w (t- t)= Asin w (t-r/ u) (2.7)
где r- расстояние от точечного источника. Волновые поверхности и фронт волны являются сферами, поэтому волна называется сферической. У цилиндрической волны фронт и волновые поверхности имеют вид коаксиальных цилиндров, их осью является источник.
 Из уравнений (2.4) и (2.7) видно, что каждая точка волнового поля колеблется гармонически, и что в каждый момент времени смещения разных точек луча являются гармонической функцией координаты. Таким образом, волна - периодический процесс в пространстве и во времени. На рис. 2.2 представлена “фотография“ волны, бегущей вдоль оси х. Характеристикой пространственной периодичности служит длина волны l. Длиной волны называется расстояние между двумя ближайшими точками, лежащими на одном луче и колеблющимися одинаково.
Из уравнений (2.4) и (2.7) видно, что каждая точка волнового поля колеблется гармонически, и что в каждый момент времени смещения разных точек луча являются гармонической функцией координаты. Таким образом, волна - периодический процесс в пространстве и во времени. На рис. 2.2 представлена “фотография“ волны, бегущей вдоль оси х. Характеристикой пространственной периодичности служит длина волны l. Длиной волны называется расстояние между двумя ближайшими точками, лежащими на одном луче и колеблющимися одинаково.
Фазы колебаний этих точек отличаются на 2p:
j 1 - j 2 = w (t-x1/ u)- w (t-x2/ u)= 2p. Учитывая, что l =x2-x1, получим,
l = u T = u / n (2.8)
Таким образом, за время, равное периоду колебаний, волна (ее фронт) успевает распространиться на расстояние, равное длине волны. Используя понятие длины волны, уравнение луча можно записать в виде:
x (x,t)=A sin(w t- 2p x/ l)= A sin(w t-kx) (2.9)
где k= 2p x/ l = w / u - волновое число. Оно показывает, сколько длин волн (пространственных периодов) укладывается на 2pметрах и аналогично круговой частоте w, показывающей, сколько временных периодов T укладывается в промежутке времени 2p секунд.
Упругая волна, возбуждаемая в стержне (рис.2.1), представляет собой распространение деформаций сжатия и растяжения, так что колебания точек стержня происходят вдоль направления распространения волны. Такая волна называется продольной. Формула (2.5) выражает скорость распространения упругих продольных волн в твердом теле. Распространение деформаций сдвига в твердых телах, например, волны в струне, связано с колебаниями точек в перпендикулярном к лучу направлении. Такая волна называется поперечной. Ее скорость распространения
u =  (2.10)
(2.10)
(G - модуль сдвига) может быть получена тем же способом, что и формула (2.5).
В жидкостях и газах могут распространяться только продольные волны, так как в этих средах возможны упругие деформации сжатия и разрежения, но не бывает деформаций сдвига. При распространении упругих волн в газах, например, звука в воздухе, чередование сжатия и разрежения в локальных областях происходит настолько быстро, что эти процессы можно считать адиабатическими. Скорость распространения упругих волн в газе выражается формулой
u =  (2.11)
(2.11)
где g =Сp/Cv - показатель адиабаты, R - молярная газовая постоянная, T - абсолютная температура, M - молярная масса. В частности, скорость звука в воздухе вычисляется по формуле u = 20,1  и при температуре t= 0оC равна 332 м/с.
и при температуре t= 0оC равна 332 м/с.
§ 2.2. Электромагнитные волны
Электромагнитные волны представляют собой распространяющееся в пространстве электромагнитное поле. Теоретически их существование было предсказано в 1865 г. Дж. К. Максвеллом, их экспериментальное наблюдение впервые осуществил Г. Герц в 1888 г.
Законы электромагнетизма, записанные в виде знаменитых уравнений Максвелла, констатируют механизм возникновения электрических и магнитных полей:
- электрическое поле создают во-первых, электрические заряды (это выражает теорема Гаусса), во-вторых, изменяющееся со временем магнитное поле (явление электромагнитной индукции);
- магнитное поле создают во-первых, движущиеся электрические заряды (токи), во-вторых, изменяющееся со временем электрическое поле.
Таким образом, электрические и магнитные поля взаимосвязаны друг с другом. Если в какой-либо области пространства возникнет переменное электрическое поле, то оно создаст переменное магнитное поле, которое, в свою очередь, индуцирует переменное электрическое поле и т. д. “Цепляясь” друг за друга, они образуют две неразрывные составляющие единого электромагнитного поля, которое может существовать в свободном пространстве (где нет ни зарядов, ни токов) в форме электромагнитных волн как самостоятельного вида материи. Применение уравнений Максвелла к подобной ситуации дает такие уравнения:
 (2.12 a)
(2.12 a)
 (2.12 б)
(2.12 б)
Напомним, что E и H - соответственно напряженности электрического и магнитного полей, e 0 и m 0 - электрическая и магнитная постоянные, e и m - диэлектрическая и магнитная проницаемость среды соответственно. Сравнивая формулы (2.12 a) и (2.12 б) с формулой (2.6), видим, что E и H представляют собой плоские бегущие волны вида (2.9), распространяющиеся с фазовой скоростью
u = 1/  (12.13)
(12.13)
В вакууме e =1, m =1, так что u = 1/  =1/
=1/  =3.10 8 м/с, т.е. любая электромагнитная волна в свободном пространстве распространяется со скоростью света с =3.108 м/с. Из этого свойства, в частности, следует, что в отличие от других видов материи, свободное электромагнитное поле не может находиться в состоянии покоя. В веществе скорость распространения u =с /
=3.10 8 м/с, т.е. любая электромагнитная волна в свободном пространстве распространяется со скоростью света с =3.108 м/с. Из этого свойства, в частности, следует, что в отличие от других видов материи, свободное электромагнитное поле не может находиться в состоянии покоя. В веществе скорость распространения u =с /  . Решения волновых уравнений (2.12 a) и (2.12 б) имеют вид:
. Решения волновых уравнений (2.12 a) и (2.12 б) имеют вид:
E=Em sin(w t - 2 p x/ l) (2.14 a)
H=Hm sin(w t - 2 p x/ l) (2.14 б)
и являются плоской бегущей электромагнитной волной. Ее ”фотография”, т. е. распределение векторов напряженности электрического E и магнитного H полейвдоль луча в один и тот же момент времени представлена на рис. 2.3.

Рис. 2.3
Перечислим свойства плоской электромагнитной волны:
1) В электромагнитной волне обязательно присутствуют оба поля E и H, при этом E ^ H.
2) Колебания электрического и магнитного полей в плоской электромагнитной волне происходят синфазно, при этом  E =
E =  H. Таким образом, для описания волны достаточно одного из двух уравнений (2.4a) или (2.4б).
H. Таким образом, для описания волны достаточно одного из двух уравнений (2.4a) или (2.4б).
3) Электромагнитные волны поперечные. Это означает, что колебания векторов E и H происходят перпендикулярно вектору скорости распространения волны u. Векторы u, E, H образуют правую тройку подобно ортам i, j, k, указывающим направление декартовых осей координат.
4) В вакууме скорость распространения электромагнитных волн любой частоты равна скорости света с= 3.108 м/с. Это, а также другие свойства электромагнитных волн доказывают, что свет является электромагнитной волной.
5) Электромагнитная волна, как и упругая, переносит энергию (возмущение)
§ 2.3. Энергия волн
Волна переносит энергию от источника колебаний к приемнику, который превращает волновую энергию в другой вид энергии (механическую, электрическую, тепловую и т.п.). Для определенности рассмотрим упругую волну в стержне (рис. 2.1). При ее распространении точки среды колеблются со скоростью υ кол=d x /dt, создавая в каждой единице объема волнового поля дополнительную кинетическую энергию с объемной плотностью
w к =1/2 r υ кол =1/2 r (d x /dt)2 (2.15 a)
Деформации сжатия и растяжения создают дополнительную потенциальную энергию с объемной плотностью
wn=1/2E e 2 =1/2E(d x /dx)2 (2.15 б)
Из формул (2.4) и (2.5) следует, что wк = wn, так что каждая единица объема волны содержит энергию
w=w к +wn= r A2 w 2 cos2(w (t-x/v)) (2.16)
Из формулы (2.16) видно, что объемная плотность энергии в каждой точке пространства, например, вблизи приемника, изменяется с частотой 2 w. Так, звуковая частота, к которой наиболее восприимчиво человеческое ухо, составляет порядка 103Гц. Обычно приемники вследствие своей инерционности регистрируют не мгновенное, а среднее по времени значение энергии. Среднее значение квадрата косинуса равно 1/2, так что среднее значение объемной плотности энергии в каждой точке пространства составляет
< w>=1/2 r A2 w 2. (2.17)
 Выделим небольшой объем волнового поля D V (рис.2.4) в виде прямоугольного параллелепипеда. Его боковая грань площадью D S ^ перпендикулярна скорости распространения волны υ. Содержащаяся в этом объеме энергия D W =w D V =w D S ^ υ D t за время D t будет перенесена волной через поверхность D S ^.. Количество энергии, переносимое волной в единицу времени через поверхность единичнойплощади, перпендикулярную лучу, называется плотностью потока энергии:
Выделим небольшой объем волнового поля D V (рис.2.4) в виде прямоугольного параллелепипеда. Его боковая грань площадью D S ^ перпендикулярна скорости распространения волны υ. Содержащаяся в этом объеме энергия D W =w D V =w D S ^ υ D t за время D t будет перенесена волной через поверхность D S ^.. Количество энергии, переносимое волной в единицу времени через поверхность единичнойплощади, перпендикулярную лучу, называется плотностью потока энергии:
J = D W /(D S ^ D t)= wυ (2.18а)
Плотность потока энергии является вектором, направленным вдоль луча, он называется вектором Умова:
J = w υ (2.18б)
Электромагнитная волна переносит энергию электрического и магнитного полей, и ее объемная плотность энергии w = w э + w м =  . В плоской электромагнитной волне электрическое и магнитное поля колеблются синфазно, а их напряженности взаимосвязаны (см. в предыдущем параграфе свойства электромагнитной волны), так что w =
. В плоской электромагнитной волне электрическое и магнитное поля колеблются синфазно, а их напряженности взаимосвязаны (см. в предыдущем параграфе свойства электромагнитной волны), так что w = 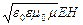 . Подставляя этот результат в формулу (2.12) и учитывая, что скорость распространения электромагнитной волны v =
. Подставляя этот результат в формулу (2.12) и учитывая, что скорость распространения электромагнитной волны v =  , получаем, что плотность потока энергии электромагнитной волны J = EH. Вектор плотности потока энергии электромагнитной волны называют вектором Пойнтинга (так исторически сложилось) и обозначают S. Вектор плотности потока энергии направлен по вектору скорости v, который с векторами Е и Н образует правую тройку, так что вектор Пойнтинга равен векторному произведению векторов напряженности электрического и магнитного полей:
, получаем, что плотность потока энергии электромагнитной волны J = EH. Вектор плотности потока энергии электромагнитной волны называют вектором Пойнтинга (так исторически сложилось) и обозначают S. Вектор плотности потока энергии направлен по вектору скорости v, который с векторами Е и Н образует правую тройку, так что вектор Пойнтинга равен векторному произведению векторов напряженности электрического и магнитного полей:
S = [ EH ] (2.19)
§ 2.4. Волны и передача информации
Информацию об окружающем мире мы получаем с помощью своих органов чувств: слуха, зрения, осязания и т.д. Волны механические в определенном диапазоне частот мы осязаем и слышим, электромагнитные видим. Приборы позволяют очень сильно расширить диапазон частот регистрируемых волн. Каждая монохроматическая волна сообщает приемнику информацию о частоте (высоте звука или цвете света) и об амплитуде (энергии, т.е. интенсивности сигнала). Для передачи конкретной информации волну модулируют, изменяя по определенному закону ее амплитуду, частоту или фазу. В § 1.3, рассматривая биения, мы получили пример амплитудной модуляции волны. Если складывать не две волны, а группу волн с разными частотами, то можно получить так называемый волновой пакет. Он представляет собой распространяющееся в пространстве волновое поле малого объема, переносящее энергию от источника к приемнику в виде импульса малой длительности Δ t. Волновой пакет используется как целое и не несет «внутри себя» никакой информации. Его можно считать единицей информации. Варьируя длительность пакетов или пауз между ними, можно передавать большой объем информации. Именно так работает азбука Морзе. Современные способы передачи информации основаны на «уплотнении» ее во времени и соответственном повышении скорости передачи. Для этого длительность «точек» и «тире» должна быть как можно меньше, а так как она не может быть меньше периода колебаний, то «несущая» частота должна быть как можно выше. Поэтому от радиоволн (108 Гц) переходят к оптическому диапазону (1015 Гц), при этом существенно возрастает емкость телевизионных и телефонных каналов и быстродействие ЭВМ. Резюмируя, отметим, что волны – универсальный и главный способ передачи информации.
Р А З Д Е Л 1. Ф И З И К А К О Л Е Б А Н И Й И В О Л Н
Глава I. Свободные колебания.
§ 1.1. Гармонический осциллятор.
 Рассмотрим груз, закрепленный на упругой пружине. Эта физическая система называется пружинным маятником, если груз можно считать материальной точкой, а пружину - невесомой и идеально упругой. При деформации пружины груз движется вдоль оси x, начало которой (х= 0) совместим с положением равновесия груза (рис1 - а). Растяжению пружины соответствует х >0, сжатию - х< 0. Сместим груз из положения равновесия (рис1 - б)., отпустим его и рассчитаем его дальнейшее движение. Для этого составим и решим уравнение движения. Для материальной точки таковым является уравнение второго закона Ньютона: m a = S F. Будем считать, что трение при движении груза пренебрежимо мало. На груз действуют три силы: тяжести m g, реакция опоры N и упругости пружины F. Движение груза одномерное. Проекции на ось x силы тяжести и реакции опоры равны нулю, силы упругости F= -kx, так что уравнение движения в проекции на ось x примет вид: ma = - kx. Учитывая, что a=d2x/dt2, получили md2x/dt2 = -kx, где m -масса и k -коэффициент жесткости - постоянные. Введем новую постоянную:
Рассмотрим груз, закрепленный на упругой пружине. Эта физическая система называется пружинным маятником, если груз можно считать материальной точкой, а пружину - невесомой и идеально упругой. При деформации пружины груз движется вдоль оси x, начало которой (х= 0) совместим с положением равновесия груза (рис1 - а). Растяжению пружины соответствует х >0, сжатию - х< 0. Сместим груз из положения равновесия (рис1 - б)., отпустим его и рассчитаем его дальнейшее движение. Для этого составим и решим уравнение движения. Для материальной точки таковым является уравнение второго закона Ньютона: m a = S F. Будем считать, что трение при движении груза пренебрежимо мало. На груз действуют три силы: тяжести m g, реакция опоры N и упругости пружины F. Движение груза одномерное. Проекции на ось x силы тяжести и реакции опоры равны нулю, силы упругости F= -kx, так что уравнение движения в проекции на ось x примет вид: ma = - kx. Учитывая, что a=d2x/dt2, получили md2x/dt2 = -kx, где m -масса и k -коэффициент жесткости - постоянные. Введем новую постоянную:
w 2 = k/m (1.1)
Уравнение движения примет вид дифференциального уравнения второго порядка с постоянными коэффициентами без правой части:
 (1.2)
(1.2)
Из математики известно[1], что его решение имеет вид гармонической функции:
x=A sin(w t + j 0)=A cos(wt + j 0 ’) (1.3)
где A, j 0, j 0 ’ - постоянные, зависящие от начальных условий, при этом j 0 = j 0 ’ + p /2.
Выясним физический смысл полученного результата.
x - координата, т.е. смещение груза из положения равновесия представляет собой знакопеременную величину. Почему? Упругая сила всегда направлена к положению равновесия и, казалось бы, должна вернуть груз в точку x= 0. Однако по мере приближения к ней скорость груза растет, он по инерции минует эту точку, и его смещение меняет знак, увеличиваясь по модулю. Теперь направления упругой силы и скорости противоположны, так что движение замедляется, пока скорость не уменьшится до нуля. После этого груз, ускоряясь, начинает двигаться к положению равновесия, и рассмотренный процесс повторяется. Такое многократно повторяющееся изменение состояния физической системы называют колебаниями.
Колебания свойственны различным формам движения материи и хорошо знакомы нам. Примеры механических колебаний - движения маятников, шатунов, рессор, морские приливы и отливы, звук. Примеры электромагнитных колебаний - переменный электрический ток, процессы в колебательных контурах различных приемников и передатчиков электромагнитных средств связи, свет и т. д. По образному выражению крупного российского физика начала ХХ века Мандельштама в физике есть языки “национальные”- механики, акустики, оптики, электродинамики и есть “интернациональный” язык теории колебаний. Колебания любой физической природы описываются одинаковым математическим аппаратом, поэтому мы подробно рассмотрим только механические колебания и используем упомянутую аналогию при рассмотрении колебаний другой физической природы.
Общими для возникновения колебаний любой природы являются два условия. Первое состоит в том, что система имеет положение устойчивого равновесия. Это означает, что такому положению соответствует минимум потенциальной энергии системы, и что при отклонении от него возникает возвращающая сила F= -kx (в рассматриваемом случае это упругая сила), стремящаяся вернуть систему в равновесие. Второе условие - это инерционность системы, которая не позволяет ей остановиться в положении равновесия.
Колебания, которые совершает система, выведенная из положения равновесия и предоставленная самой себе, называются свободными. Если система колеблется под действием только внутренних сил (силами трения можно пренебречь), как в рассмотренном примере пружинного маятника, то ее колебания называются собственными.
Движение (процесс) называется периодическим, если каждое состояние системы повторяется через определенный промежуток времени. Его называют периодом - Т. Из этого определения следует:
x(t)=x(t+nT) (1.4)
где n -любое целое число.
Другая характеристика периодических процессов - частота n равна числу колебаний в единицу времени. Следовательно,
n = 1 /T (1.5)
Простейшим типом периодических колебаний являются гармонические, при которых изменение характеристик состояния системы происходит по гармоническому закону, т.е. по закону синуса или косинуса (1.3). Этот тип колебаний часто встречается в природе и в технике, он наиболее прост с точки зрения математического описания и, что особенно важно, периодический процесс любого вида (и даже не периодический) может быть представлен как сумма конечного или бесконечного числа гармонических колебаний с разными частотами. В математике такому гармоническому анализу соответствует разложение в ряд Фурье, в физике - разложение в спектр. Спектральный анализ широко применяется в науке и в технике. Таким образом, изучение гармонических колебаний открывает широкие возможности анализа и понимания различных физических процессов.
Система, совершающая колебания, называется осциллятором (от латинского oscillare -колебаться). Закон движения гармонического осциллятора выберем в виде (см.формулу 1.3):
x =A sin(w t+ j 0) (1.6)
и вспомним известный из школы смысл входящих в него величин.
x - смещение, т.е. отклонение колеблющейся величины от положения равновесия, принятого за начало отсчета.
A - амплитуда, т.е. максимальное смещение, A=const. В нашем примере (рис.1) амплитуда равна начальному смещению груза из положения равновесия, т.е. величину амплитуды задает сообщенная системе энергия колебаний,
j =(w t+ j 0) - фаза колебаний, аргумент гармонической функции, в СИ измеряется в радианах j 0 - значение фазы при t =0 называют начальной фазой. Фаза определяет состояние системы в каждый момент времени и является линейной функцией времени. Если два колебания имеют разные фазы, то говорят, что они сдвинуты по фазе. При сдвиге по фазе на p говорят, что колебания происходят в противофазе. Колебания с одинаковыми фазами или с разностью фаз, кратной 2p, называют синфазными.
w - круговая или циклическая частота, в СИ измеряется в рад/с. Из формулы (1.2) видно, что частота определяется параметрами колебательной системы: упругостью и массой маятника и не зависит от величины начального смещения. Используя соотношения (1.4) и (1.5), самостоятельно убедитесь в том, что
w = 2p/ T= 2p n (1.7)
Таким образом, круговая (циклическая) частота равна числу колебаний за 2p единиц времени и является аналогом угловой скорости при вращательном движении, если под T понимать период вращения.
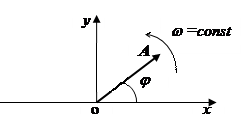 Аналогию между колебательным и вращательным движениями можно продолжить, рассматривая фазу колебаний как угол поворота и изображая гармоническое колебание вектором (рис. 1.2). Пусть вектор, модуль которого равен амплитуде колебаний A, равномерно вращается в плоскости xy вокруг неподвижного центра O с постоянной угловой скоростью w. Угол j, образованный им с осью диаграммы, равен фазе колебаний. Проекции вектора на оси диаграммы x и y изменяются по гармоническому закону, причем закону в форме (1.6) соответствует проекция на ось y.
Аналогию между колебательным и вращательным движениями можно продолжить, рассматривая фазу колебаний как угол поворота и изображая гармоническое колебание вектором (рис. 1.2). Пусть вектор, модуль которого равен амплитуде колебаний A, равномерно вращается в плоскости xy вокруг неподвижного центра O с постоянной угловой скоростью w. Угол j, образованный им с осью диаграммы, равен фазе колебаний. Проекции вектора на оси диаграммы x и y изменяются по гармоническому закону, причем закону в форме (1.6) соответствует проекция на ось y.
Вернемся к рассмотрению пружинного маятника. Как следует из формул (1.1) и (1.7), его период колебаний:
T =2p  (1.8)
(1.8)
В рассматриваемом нами примере пружинного маятника его движение задано внутренними силами, поэтому формулы (11.1) и (11.8) выражают соответственно круговую частоту и период собственных колебаний. Обратите внимание, что они заданы собственными параметрами колебательной системы - m и k и не зависят от начальных условий, в частности, от амплитуды колебаний. Чем больше инертность (масса) маятника, тем медленнее изменяется его движение. С другой стороны, чем больше жесткость пружины, тем быстрее реагирует груз на ее воздействие.
Проанализируем другие характеристики гармонического колебательного движения, используя известные из механики соотношения u =dx/dt, a=d u /dt, F=ma. Помимо смещения - x гармонически изменяются скорость - u, ускорение - a, возвращающая сила - F, причем, все они колеблются с одинаковыми частотами. Убедитесь в этом самостоятельно, а также в том, что соответствующие амплитуды равны:
u max =A v, amax=A v 2, Fmax=ma v 2 (1.9)
и что сдвиг по фазе между скоростью и смещением составляет p/2, ускорение и смещение колеблются в противофазе, а колебания возвращающей силы и ускорения синфазны.
Для возбуждения колебаний систему надо вывести из положения равновесия, т.е. сообщить ей дополнительную энергию. Возвращающая сила F= -kx создает потенциальную энергию:
W п = kx2/2 = (kA2/2) sin2(w t+ j 0 ) (1.10)
Движущееся тело обладает энергией кинетической
Wк =m u 2 /2 = (mA2 v 2 /2) cos2(v t+ j 0). (1.11)
Значения потенциальной и кинетической энергий при колебаниях изменяются, при этом полная механическая энергия сохраняется:
W=Wк+Wп = kA2/2 = mA2/2 (1.12)
Это закономерно, так как колебания осциллятора происходят под действием консервативной силы. Проанализируйте самостоятельно, в каких состояниях осциллятор имеет только потенциальную энергию, а в каких только кинетическую, и как происходят взаимные превращения этих видов энергии друг в друга.
Подведем итоги:
1. Система, уравнение движения которой имеет вид
 (1.13)
(1.13)
является гармоническим осциллятором, совершающим колебания с круговой частотой w=  .
.
2. Частота собственных колебаний определяется параметрами колебательной системы и не зависит от внешних условий, в частности, от запаса энергии, сообщенной осциллятору при возбуждении колебаний.
3. При гармонических колебаниях механического осциллятора гармонически колеблются с одинаковыми частотами и согласованными амплитудами и фазами смещение, скорость, ускорение, возвращающая сила при сохранении полной энергии, тогда как кинетическая и потенциальная энергии колеблются с удвоенной частотой.
§ 1.2. Примеры гармонических осцилляторов.
Реальные физические системы при малых отклонениях от положения равновесия можно считать гармоническими осцилляторами, если силы сопротивления малы. Рассмотрим такие системы.
 1) Физический маятник
1) Физический маятник
Тело, подвешенное на горизонтальной оси, не проходящей через его центр тяжести, и выведенное из положения равновесия, качается под действием силы тяжести m g.. Такое твердое тело и есть физический маятник (рис.1.3) Неподвижная горизонтальная ось перпендикулярна плоскости рисунка и проходит через точку O. Центр тяжести тела – точка C. Расстояние OC обозначим b. Составим уравнение движения этого тела, для чего используем основной закон динамики вращательного движения: I e = S M, где I - момент инерции тела относительно оси O, e - угловое ускорение, e =d2 a /dt2, где a - угол отклонения прямой OC от вертикали, M - момент силы относительно оси O. На тело действует сила тяжести m g, приложенная в центре тяжести C, и сила реакции опоры, приложенная в точке O. В положении равновесия эти силы направлены вдоль прямой OC в противоположные стороны и уравновешивают друг друга, если тело покоится. При отклонении тела на угол a сила тяжести создает момент M = - mgb sin a.. Знак “ минус “ обусловлен противоположными направлениями векторов d a и M. Пренебрегая трением в подвесе и сопротивлением воздуха, получим:
d2 a /dt2 = - mgbsin a (1.14)
Для малых углов sin a» a, так что уравнение движения примет вид:
d2 a /dt2 + (mgb/ I) a = 0 (1.15)
Сравнивая (1.13) и (1.15), видим, что малые колебания физического маятника являются гармоническими с периодом
T=2 p  (1.16)
(1.16)
Примерами физических маятников могут служить маятники часов, раскачиваемые ветром линии электропередач, здания, поднимаемые грузы, перевозимые в цистернах жидкости и т. п.
2) Математический маятник - маленький груз (материальная точка) массы m, подвешенный на невесомой нерастяжимой нити длиной l. Он является частным случаем физического маятника с моментом инерции I =ml2 и расстоянием от точки подвеса до центра тяжести b=l, так что
T = 2 p  (1.17)
(1.17)
Формулу (1.17) используют для определения с высокой точностью ускорения свободного падения g, зависящего от плотности залегающих в земле пород, и применяют в геологоразведке.
Физический маятник характеризуют приведенной длиной L. Она равна длине математического маятника, колеблющегося с тем же периодом, что и физический маятник. Из сравнения формул (1.16) и (1.17) следует: L= I /mb.
Роль возвращающей силы при колебаниях физического и математического маятников играет составляющая силы тяжести, которая является консервативной, поэтому полная механическая энер



 Колебания, возбуждаемые в какой-либо области пространства, могут передаваться соседним областям, удаляясь от источника. Такой процесс распространения колебаний называется волной. Область пространства, занятую волной, называют волновым полем. Все точки волнового поля колеблются согласованно друг с другом. Волновое поле может увеличиваться в размерах и перемещаться в пространстве. Это явление широко распространено в природе и технике: достаточно вспомнить, что звук - упругие, а свет - электромагнитные волны.
Колебания, возбуждаемые в какой-либо области пространства, могут передаваться соседним областям, удаляясь от источника. Такой процесс распространения колебаний называется волной. Область пространства, занятую волной, называют волновым полем. Все точки волнового поля колеблются согласованно друг с другом. Волновое поле может увеличиваться в размерах и перемещаться в пространстве. Это явление широко распространено в природе и технике: достаточно вспомнить, что звук - упругие, а свет - электромагнитные волны. s 2 - s 1 = r a D x (2.1)
s 2 - s 1 = r a D x (2.1) (2.5)
(2.5) Из уравнений (2.4) и (2.7) видно, что каждая точка волнового поля колеблется гармонически, и что в каждый момент времени смещения разных точек луча являются гармонической функцией координаты. Таким образом, волна - периодический процесс в пространстве и во времени. На рис. 2.2 представлена “фотография“ волны, бегущей вдоль оси х. Характеристикой пространственной периодичности служит длина волны l. Длиной волны называется расстояние между двумя ближайшими точками, лежащими на одном луче и колеблющимися одинаково.
Из уравнений (2.4) и (2.7) видно, что каждая точка волнового поля колеблется гармонически, и что в каждый момент времени смещения разных точек луча являются гармонической функцией координаты. Таким образом, волна - периодический процесс в пространстве и во времени. На рис. 2.2 представлена “фотография“ волны, бегущей вдоль оси х. Характеристикой пространственной периодичности служит длина волны l. Длиной волны называется расстояние между двумя ближайшими точками, лежащими на одном луче и колеблющимися одинаково.  (2.10)
(2.10) (2.11)
(2.11) и при температуре t= 0оC равна 332 м/с.
и при температуре t= 0оC равна 332 м/с. (2.12 a)
(2.12 a) (2.12 б)
(2.12 б) (12.13)
(12.13) =1/
=1/  =3.10 8 м/с, т.е. любая электромагнитная волна в свободном пространстве распространяется со скоростью света с =3.108 м/с. Из этого свойства, в частности, следует, что в отличие от других видов материи, свободное электромагнитное поле не может находиться в состоянии покоя. В веществе скорость распространения u =с /
=3.10 8 м/с, т.е. любая электромагнитная волна в свободном пространстве распространяется со скоростью света с =3.108 м/с. Из этого свойства, в частности, следует, что в отличие от других видов материи, свободное электромагнитное поле не может находиться в состоянии покоя. В веществе скорость распространения u =с /  . Решения волновых уравнений (2.12 a) и (2.12 б) имеют вид:
. Решения волновых уравнений (2.12 a) и (2.12 б) имеют вид:
 E =
E =  H. Таким образом, для описания волны достаточно одного из двух уравнений (2.4a) или (2.4б).
H. Таким образом, для описания волны достаточно одного из двух уравнений (2.4a) или (2.4б). Выделим небольшой объем волнового поля D V (рис.2.4) в виде прямоугольного параллелепипеда. Его боковая грань площадью D S ^ перпендикулярна скорости распространения волны υ. Содержащаяся в этом объеме энергия D W =w D V =w D S ^ υ D t за время D t будет перенесена волной через поверхность D S ^.. Количество энергии, переносимое волной в единицу времени через поверхность единичнойплощади, перпендикулярную лучу, называется плотностью потока энергии:
Выделим небольшой объем волнового поля D V (рис.2.4) в виде прямоугольного параллелепипеда. Его боковая грань площадью D S ^ перпендикулярна скорости распространения волны υ. Содержащаяся в этом объеме энергия D W =w D V =w D S ^ υ D t за время D t будет перенесена волной через поверхность D S ^.. Количество энергии, переносимое волной в единицу времени через поверхность единичнойплощади, перпендикулярную лучу, называется плотностью потока энергии: . В плоской электромагнитной волне электрическое и магнитное поля колеблются синфазно, а их напряженности взаимосвязаны (см. в предыдущем параграфе свойства электромагнитной волны), так что w =
. В плоской электромагнитной волне электрическое и магнитное поля колеблются синфазно, а их напряженности взаимосвязаны (см. в предыдущем параграфе свойства электромагнитной волны), так что w = 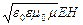 . Подставляя этот результат в формулу (2.12) и учитывая, что скорость распространения электромагнитной волны v =
. Подставляя этот результат в формулу (2.12) и учитывая, что скорость распространения электромагнитной волны v =  , получаем, что плотность потока энергии электромагнитной волны J = EH. Вектор плотности потока энергии электромагнитной волны называют вектором Пойнтинга (так исторически сложилось) и обозначают S. Вектор плотности потока энергии направлен по вектору скорости v, который с векторами Е и Н образует правую тройку, так что вектор Пойнтинга равен векторному произведению векторов напряженности электрического и магнитного полей:
, получаем, что плотность потока энергии электромагнитной волны J = EH. Вектор плотности потока энергии электромагнитной волны называют вектором Пойнтинга (так исторически сложилось) и обозначают S. Вектор плотности потока энергии направлен по вектору скорости v, который с векторами Е и Н образует правую тройку, так что вектор Пойнтинга равен векторному произведению векторов напряженности электрического и магнитного полей:  Рассмотрим груз, закрепленный на упругой пружине. Эта физическая система называется пружинным маятником, если груз можно считать материальной точкой, а пружину - невесомой и идеально упругой. При деформации пружины груз движется вдоль оси x, начало которой (х= 0) совместим с положением равновесия груза (рис1 - а). Растяжению пружины соответствует х >0, сжатию - х< 0. Сместим груз из положения равновесия (рис1 - б)., отпустим его и рассчитаем его дальнейшее движение. Для этого составим и решим уравнение движения. Для материальной точки таковым является уравнение второго закона Ньютона: m a = S F. Будем считать, что трение при движении груза пренебрежимо мало. На груз действуют три силы: тяжести m g, реакция опоры N и упругости пружины F. Движение груза одномерное. Проекции на ось x силы тяжести и реакции опоры равны нулю, силы упругости F= -kx, так что уравнение движения в проекции на ось x примет вид: ma = - kx. Учитывая, что a=d2x/dt2, получили md2x/dt2 = -kx, где m -масса и k -коэффициент жесткости - постоянные. Введем новую постоянную:
Рассмотрим груз, закрепленный на упругой пружине. Эта физическая система называется пружинным маятником, если груз можно считать материальной точкой, а пружину - невесомой и идеально упругой. При деформации пружины груз движется вдоль оси x, начало которой (х= 0) совместим с положением равновесия груза (рис1 - а). Растяжению пружины соответствует х >0, сжатию - х< 0. Сместим груз из положения равновесия (рис1 - б)., отпустим его и рассчитаем его дальнейшее движение. Для этого составим и решим уравнение движения. Для материальной точки таковым является уравнение второго закона Ньютона: m a = S F. Будем считать, что трение при движении груза пренебрежимо мало. На груз действуют три силы: тяжести m g, реакция опоры N и упругости пружины F. Движение груза одномерное. Проекции на ось x силы тяжести и реакции опоры равны нулю, силы упругости F= -kx, так что уравнение движения в проекции на ось x примет вид: ma = - kx. Учитывая, что a=d2x/dt2, получили md2x/dt2 = -kx, где m -масса и k -коэффициент жесткости - постоянные. Введем новую постоянную: (1.2)
(1.2)
 Аналогию между колебательным и вращательным движениями можно продолжить, рассматривая фазу колебаний как угол поворота и изображая гармоническое колебание вектором (рис. 1.2). Пусть вектор, модуль которого равен амплитуде колебаний A, равномерно вращается в плоскости xy вокруг неподвижного центра O с постоянной угловой скоростью w. Угол j, образованный им с осью диаграммы, равен фазе колебаний. Проекции вектора на оси диаграммы x и y изменяются по гармоническому закону, причем закону в форме (1.6) соответствует проекция на ось y.
Аналогию между колебательным и вращательным движениями можно продолжить, рассматривая фазу колебаний как угол поворота и изображая гармоническое колебание вектором (рис. 1.2). Пусть вектор, модуль которого равен амплитуде колебаний A, равномерно вращается в плоскости xy вокруг неподвижного центра O с постоянной угловой скоростью w. Угол j, образованный им с осью диаграммы, равен фазе колебаний. Проекции вектора на оси диаграммы x и y изменяются по гармоническому закону, причем закону в форме (1.6) соответствует проекция на ось y. (1.8)
(1.8) (1.13)
(1.13) .
. 1) Физический маятник
1) Физический маятник (1.16)
(1.16) (1.17)
(1.17)

