Подобный же анализ можно выполнить для экстремально ретроградного профиля легирования вместо ранее предполагаемого однородного легирования. При таком профиле легирования толщина обедненного слоя равна нелегированной толщине слоя, независимо от напряжения затвора. Анализ проще, чем в случае однородного легирования, поскольку 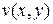 есть просто непрерывная линейная функция х для всей области
есть просто непрерывная линейная функция х для всей области 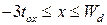 . Он также более точен, поскольку полное нижнее граничное условие
. Он также более точен, поскольку полное нижнее граничное условие 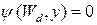 вдоль BE на рис.С1.4 удовлетворяется
вдоль BE на рис.С1.4 удовлетворяется 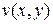 без необходимости для
без необходимости для 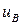 ряда. Результат подобен выражению (С1.27) с параметром а, замененным на m / 2. Так как в общем случае
ряда. Результат подобен выражению (С1.27) с параметром а, замененным на m / 2. Так как в общем случае 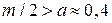 , экстремально ретроградно легированные МОПТ имеют слегка лучший ККЭ, чем в случае однородного легирования для тех же самых
, экстремально ретроградно легированные МОПТ имеют слегка лучший ККЭ, чем в случае однородного легирования для тех же самых 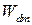 и
и 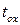 .
.
С1.10 Обобщенная характеристическая длинадля high - k диэлектриков
Когда длина канала КМОПТ уменьшается до 20-30нм, толщина оксида до ≈1нм, возникает необходимость в контроле ККЭ. Туннельный ток затвора мог быть неприемлемо высоким для таких атомарно тонких оксидов. Проблема могла быть решена путем использования диэлектриков с высокой диэлектрической проницаемостью (high-k диэлектриков) в качестве подзатворных диэлектриков. Нормальное поле (в кремнии) и емкость затвора при использовании high-k диэлектрика с диэлектрической проницаемостью 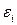 и толщиной
и толщиной
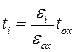 (С1.32)
(С1.32)
таковые же, как при использовании окисного слоя с диэлектрической проницаемостью 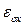 и толщиной
и толщиной 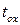 . Если
. Если 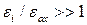 , физическая толщина high-k диэлектрика
, физическая толщина high-k диэлектрика 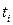 много больше, чем
много больше, чем 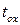 , следовательно, значительно уменьшая туннельный ток (квантово-механическое туннелирование не имеет никакого отношения к диэлектрической константе материала). На практике довольно трудно разработать high-k диэлектрик для затвора с приемлемыми характеристиками для использования в КМОП приборах. High-k диэлектрики в настоящее время одни из наиболее исследуемых объектов в области СБИС.
, следовательно, значительно уменьшая туннельный ток (квантово-механическое туннелирование не имеет никакого отношения к диэлектрической константе материала). На практике довольно трудно разработать high-k диэлектрик для затвора с приемлемыми характеристиками для использования в КМОП приборах. High-k диэлектрики в настоящее время одни из наиболее исследуемых объектов в области СБИС.
Из модели характеристической длиныдля одной области ожидается, что 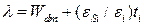 для high-k диэлектриков. Однако это справедливо только для
для high-k диэлектриков. Однако это справедливо только для 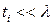 , когда преобладают нормальные (вертикальные) поля. Когда возрастают и
, когда преобладают нормальные (вертикальные) поля. Когда возрастают и 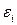 , и
, и 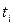 с одинаковым коэффициентом, то есть при постоянной емкости
с одинаковым коэффициентом, то есть при постоянной емкости 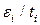 , продольные поля становятся более важными, поскольку высокая диэлектрическая постоянная их не улучшает. При произвольных диэлектрической постоянной и толщине необходимо использовать обобщенную модель двух областей для длины масштабирования, описанную в Приложении 1. При согласовании граничных условий для нормальных и тангенциальных полей на границе кремний-диэлектрик, собственные значения характеристической длиныполучаются из уравнения:
, продольные поля становятся более важными, поскольку высокая диэлектрическая постоянная их не улучшает. При произвольных диэлектрической постоянной и толщине необходимо использовать обобщенную модель двух областей для длины масштабирования, описанную в Приложении 1. При согласовании граничных условий для нормальных и тангенциальных полей на границе кремний-диэлектрик, собственные значения характеристической длиныполучаются из уравнения:
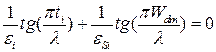 . (С1.33)
. (С1.33)
Это уравнение имеет бесконечное число решений с уменьшающейся степенью 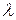 . Наименьшая степень собственного значения, или наименьшее
. Наименьшая степень собственного значения, или наименьшее 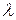 , преобладает, так как короткоканальная компонента потенциала пропорциональна
, преобладает, так как короткоканальная компонента потенциала пропорциональна 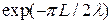 , как и в модели одной области. Уравнение (С1.33) не может быть решено аналитически. Численное решение для наибольших
, как и в модели одной области. Уравнение (С1.33) не может быть решено аналитически. Численное решение для наибольших 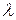 показано в нормализованных единицах на рис.С1.6 для некоторых типичных значений
показано в нормализованных единицах на рис.С1.6 для некоторых типичных значений 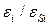 .
.
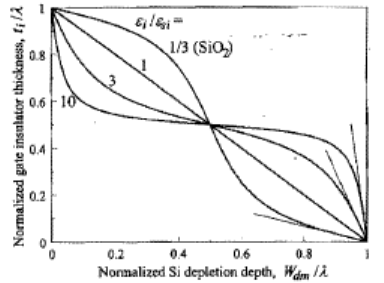
Рис.С1.6. Численное решение уравнение (С1.33) для различных значений 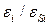 . Пунктирные линии в правом нижнем углу показывают поведение асимптотического решения
. Пунктирные линии в правом нижнем углу показывают поведение асимптотического решения 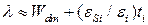 для
для 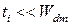 [3].
[3].
Важность  остается прежней: она предписывает минимальную длину канала,
остается прежней: она предписывает минимальную длину канала, 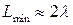 , как предсказывалось с модели одной области, обсуждавшейся выше.
, как предсказывалось с модели одной области, обсуждавшейся выше.
На рис С1.6 наблюдаются следующие особенности решения уравнения (С1.33):
· 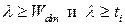 , если
, если  больше, чем
больше, чем 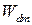 ,
, 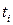 .
.
· в особом случае 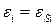 ,
, 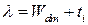 , физической высоте в боксе на
, физической высоте в боксе на
рис. С4.1.
· в особом случае 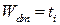 ,
, 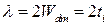 , независимо от
, независимо от 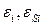 .
.
· если 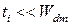 (нижний правый угол на рис.3.26),
(нижний правый угол на рис.3.26), 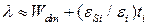 . Это приближенное решение получается в модели одной области.
. Это приближенное решение получается в модели одной области.
· если 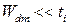 (верхний левый угол на рис.3.26),
(верхний левый угол на рис.3.26), 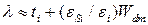 .
.
В то время как выражение (С1.33)и рис.С1.6. симметричны относительно 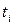 и
и 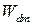 , анализ
, анализ 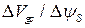 или m -фактора требуют, чтобы
или m -фактора требуют, чтобы 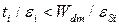 . Другими словами, для
. Другими словами, для 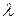 приемлемо только решение в нижнем правом углу рис.С1.6.. В этой области high-k диэлектрик помогает, так как
приемлемо только решение в нижнем правом углу рис.С1.6.. В этой области high-k диэлектрик помогает, так как 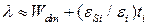 , и для того же самого
, и для того же самого 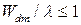 более высокое
более высокое 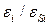 позволяет большее отношение
позволяет большее отношение 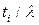 . Однако, вследствие чрезвычайной нелинейности кривой для
. Однако, вследствие чрезвычайной нелинейности кривой для 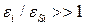 решение для
решение для  быстро отклоняется от выше рассмотренной модели одной области (линейная аппроксимация – пунктиры на рис.С1.6.), когда
быстро отклоняется от выше рассмотренной модели одной области (линейная аппроксимация – пунктиры на рис.С1.6.), когда 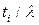 возрастает. Существует предел
возрастает. Существует предел 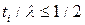 или
или 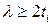 , где
, где 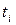 − физическая толщина изолятора независимо от того, как велика его диэлектрическая постоянная. Физически это обусловлено продольными полями, в отличие от вертикальных полей, не затрагиваемых диэлектрической константой материала. В приборах с очень толстым и с очень высокой диэлектрической константой high-k диэлектриком доминируют продольные поля, так что характеристическая длинаопределяется главным образом физической толщиной пленки.
− физическая толщина изолятора независимо от того, как велика его диэлектрическая постоянная. Физически это обусловлено продольными полями, в отличие от вертикальных полей, не затрагиваемых диэлектрической константой материала. В приборах с очень толстым и с очень высокой диэлектрической константой high-k диэлектриком доминируют продольные поля, так что характеристическая длинаопределяется главным образом физической толщиной пленки.
Заметим, что для 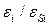 <1, то есть SiO2, кривизна кривой на рис.С1.6. противоположна той, что при
<1, то есть SiO2, кривизна кривой на рис.С1.6. противоположна той, что при 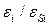 >1. Это значит, что
>1. Это значит, что  всегда ниже (лучше), чем аппроксимация одной областью,
всегда ниже (лучше), чем аппроксимация одной областью, 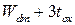 , так как
, так как 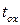 увеличивается.
увеличивается.
Литература
1. Taur, Y., Hu, G. J., Dennard, R H., Terman, L. M., Ting, C. Y. and Petrillo, K. E. (1985), A selfaligned 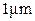 channel CMOS technology with retrograde n-well and thin epitaxy, IEEE Trans. Electron Devices ED-32, 203-209.
channel CMOS technology with retrograde n-well and thin epitaxy, IEEE Trans. Electron Devices ED-32, 203-209.
2. Troutman, R. R (1979). VLSI limitations from drain-induced barrier lowering, IEEE Trans. Electron Devices ED-26, 461-469.
3. Yuan Taur, Tak H. Ning, Fundamentals of Modern VLSI Device, Cambridge University Press, 2009.
4. Taur, Y., CMOS design near the limit of scaling, IBM J. RES. & DEV. VOL. 46 NO. 2/3 MARCH/MAY 2002, р. 213-221.
5. Nguyen, T. N. (1984). Small-geometry MOS transistors: physics and modeling of surface-and buried-channel MOSFETs. Ph. D. thesis, Stanford University.
6. Приложение 1. Обобщенная модель длины масштабирования МОПТ.
Задание для СРС
1. Ознакомиться с методические указаниями студентам по изучению дисциплины «Физика наноразмерных полупроводниковых структур» (Приложение 2).
2. Пользуясь материалом семинара №1 рассчитать величину короткоканального спада порогового напряжения и величину подпорогового размаха пМОПТ со следующими параметрами областей: 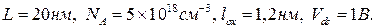
3. Самостоятельно изучить материал Приложения 1 к семинару 1.
4. Получить у преподавателя индивидуальное задание для подготовки реферата и выступления на семинаре.
Приложение 1 к семинару 1
Обобщенная модель характеристической длиныМОПТ
Рассмотренная на семинаре 1 модель характеристической длины называется моделью одной области. Она заменяет толщину окисла эквивалентной областью с той же диэлектрической проницаемостью, что и у кремния. но с толщиной, равной 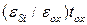 или
или 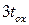 . Как указывалось, это корректно определяет нормальное поле (
. Как указывалось, это корректно определяет нормальное поле (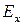 ), но тангенциальное поле (
), но тангенциальное поле (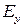 ) – некорректно. Модель одной области справедлива, только если толщина окисла много тоньше, чем характеристическая длина
) – некорректно. Модель одной области справедлива, только если толщина окисла много тоньше, чем характеристическая длина  , при котором в окисле преобладает нормальная компонента. В [1] опубликована модель обобщенной характеристической длины,которая распространяет модель одной области на две и три области с произвольными диэлектрическими постоянными и толщинами. Она рассматривает различные граничные условия для нормальных и тангенциальных полей отдельно на диэлектрических границах. Эти соотношения тогда приводят к уравнениям на собственные значения, которые могут быть решены для характеристической длины
, при котором в окисле преобладает нормальная компонента. В [1] опубликована модель обобщенной характеристической длины,которая распространяет модель одной области на две и три области с произвольными диэлектрическими постоянными и толщинами. Она рассматривает различные граничные условия для нормальных и тангенциальных полей отдельно на диэлектрических границах. Эти соотношения тогда приводят к уравнениям на собственные значения, которые могут быть решены для характеристической длины  в таких общих структурах.Обобщенная модель характеристической длиныочень важна для high-k диэлектриков, которые могут быть физически толстыми, а также и для КНИ и двухзатворных МОПТ.
в таких общих структурах.Обобщенная модель характеристической длиныочень важна для high-k диэлектриков, которые могут быть физически толстыми, а также и для КНИ и двухзатворных МОПТ.
П1.1 Уравнение для характеристической длиныв модели двух областей
В этом приложении описывается вывод обобщенной характеристической длиныМОПТ. Рассмотрим модель двух областей МОПТ, представленную на рис.П1.1. Предполагается, что область подзатворного изолятора имеет диэлектрическую проницаемость 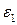 и толщину t 1. Обедненная область полупроводника имеет диэлектрическую проницаемость
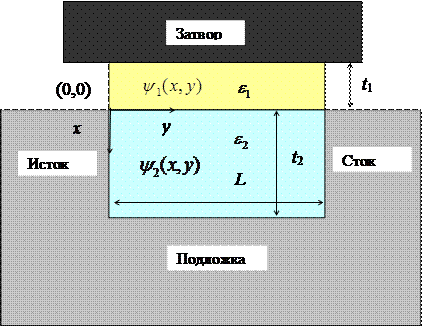
и толщину t 1. Обедненная область полупроводника имеет диэлектрическую проницаемость 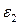 и толщину t 2. Заметим, что нижняя граница обедненной области упрощена до прямой линии тем же образом, как на рис.С1.4. В подпороговой области пренебрегается подвижными носителями в инверсной области. Электрический потенциал находится из решения двумерного уравнения Пуассона, примененного к прямоугольной области на рис П1.1.Существует проблема граничного условия, в которой требуется точно определить потенциал на четырех проводящих сторонах прямоугольника, левой (исток), верхней (затвор), правой (сток), нижней (подложка). Имеется реально два малых зазора, не огороженных проводниками: наверху слева между затвором и истоком и наверху справа между затвором и стоком. Когда эти зазоры не чрезмерно велики (по сравнению с, например,
и толщину t 2. Заметим, что нижняя граница обедненной области упрощена до прямой линии тем же образом, как на рис.С1.4. В подпороговой области пренебрегается подвижными носителями в инверсной области. Электрический потенциал находится из решения двумерного уравнения Пуассона, примененного к прямоугольной области на рис П1.1.Существует проблема граничного условия, в которой требуется точно определить потенциал на четырех проводящих сторонах прямоугольника, левой (исток), верхней (затвор), правой (сток), нижней (подложка). Имеется реально два малых зазора, не огороженных проводниками: наверху слева между затвором и истоком и наверху справа между затвором и стоком. Когда эти зазоры не чрезмерно велики (по сравнению с, например,  ), хорошим приближением является задание потенциала в виде линейной интерполяции между потенциалами затвора и истока для левого зазора и между потенциалами затвора и стока для правого зазора.
), хорошим приближением является задание потенциала в виде линейной интерполяции между потенциалами затвора и истока для левого зазора и между потенциалами затвора и стока для правого зазора.
 Используя тот же метод суперпозиции, что и в семинаре 1, решение для потенциала внутри выделенных областей,
Используя тот же метод суперпозиции, что и в семинаре 1, решение для потенциала внутри выделенных областей, 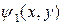 для области 1 и
для области 1 и 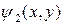 для области 2, может быть разложено на несколько компонент.
для области 2, может быть разложено на несколько компонент.
Рис П1.1Схематическая диаграмма МОПТ в модели двух областей.
Первая компонента – решение одномерного уравнения Пуассона в направлении х, которое удовлетворяет неоднородному (длинноканальному) уравнению и верхнему и нижнему граничным условиям. Другие два компонента являются решениями однородного двумерного уравнения Лапласа и выбраны для того, чтобы удовлетворить левому (исток) и правому (сток) граничным условиям, соответственно. В семинаре 1 показано, что последние члены ответственны за ККЭ. Левая (исток) и правая (сток) компоненты 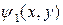 могут быть записаны как
могут быть записаны как
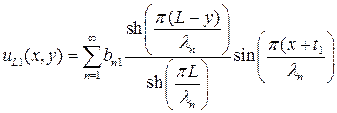 (П1.1)
(П1.1)
и 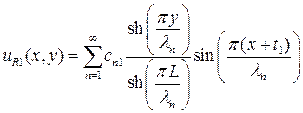 (П1.2)
(П1.2)
Заметим, что каждый член рядов 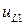 и
и 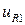 удовлетворяет уравнению Лапласа, например,
удовлетворяет уравнению Лапласа, например, 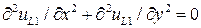 для любого
для любого  . Также заметим, что
. Также заметим, что 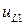 принимает нулевое значение на верхней (
принимает нулевое значение на верхней (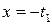 ) и правой (
) и правой (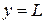 ) границах, в то время как
) границах, в то время как 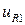 принимает нулевое значение на верхней и левой (
принимает нулевое значение на верхней и левой (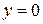 ) границах. Подобным же образом, левая и правая компоненты
) границах. Подобным же образом, левая и правая компоненты 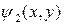 равны
равны
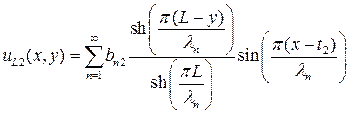 (П1.3)
(П1.3)
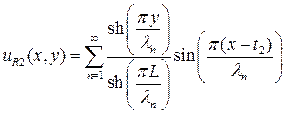 , (П1.4)
, (П1.4)
так что 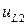 принимает нулевое значение на нижней (
принимает нулевое значение на нижней (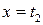 ) и правой (
) и правой (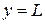 ) границах, в то время как
) границах, в то время как 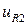 принимает нулевое значение на нижней и левой (
принимает нулевое значение на нижней и левой (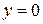 ) границах.
) границах.
На общей границе совместно для 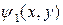 и
и 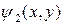 ,
, 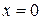 , при нормальном перемещении через границу величина
, при нормальном перемещении через границу величина 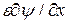 , также как потенциал
, также как потенциал 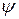 (следовательно, тангенциальное поле,
(следовательно, тангенциальное поле, 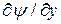 ) должны быть непрерывны при переходе из одной диэлектрической среды в другую. Вследствие различия формы функций от у, каждый член в
) должны быть непрерывны при переходе из одной диэлектрической среды в другую. Вследствие различия формы функций от у, каждый член в 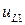 и
и 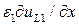 должен быть равен их аналогу в
должен быть равен их аналогу в 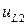 и
и 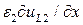 при
при 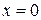 . Следовательно, получаем
. Следовательно, получаем
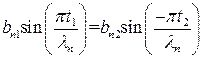 (П1.5)
(П1.5)
и 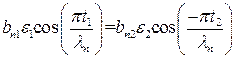 . (П1.6)
. (П1.6)
Подобные же соотношения получаются для 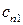 и
и 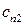 из
из 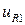 и
и 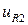 и их производных. Для ненулевых решений
и их производных. Для ненулевых решений 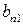 и
и 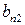 выражения (П1.5) и (П1.6) могут быть поделены друг на друга, чтобы получить уравнение для собственных значений
выражения (П1.5) и (П1.6) могут быть поделены друг на друга, чтобы получить уравнение для собственных значений 
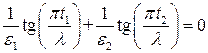 . (П1.7)
. (П1.7)
Здесь собственные значения, обозначенные как  , имеют дискретный ряд решений,
, имеют дискретный ряд решений, 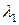 ,
, 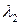 ,
, 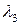 ,
, 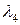 , в нисходящем порядке. Наибольшее собственное значение является и наиболее важным, так как каждый член короткоканального вклада в потенциал пропорционален
, в нисходящем порядке. Наибольшее собственное значение является и наиболее важным, так как каждый член короткоканального вклада в потенциал пропорционален  [смотри семинар 1, например, выражение (С1.26)]. В полной короткоканальной части потенциала доминирует член с наибольшим
[смотри семинар 1, например, выражение (С1.26)]. В полной короткоканальной части потенциала доминирует член с наибольшим  , то есть
, то есть 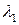 . Члены более высокого порядка в выражениях (П1.1) - (П1.4) пренебрежимо малы при условии, что длина канала не сравнима или короче, чем
. Члены более высокого порядка в выражениях (П1.1) - (П1.4) пренебрежимо малы при условии, что длина канала не сравнима или короче, чем 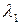 .
.
Для данных 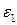 ,
, 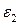 ,
, 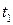 ,
, 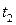 уравнение (П1.7) может бать решено относительно характеристической длины
уравнение (П1.7) может бать решено относительно характеристической длины  (используемой попеременно с
(используемой попеременно с 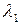 ), которая является эквивалентом двух областей вместо
), которая является эквивалентом двух областей вместо 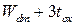 . ККЭ приемлемы, если
. ККЭ приемлемы, если 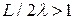 . Другими словами,
. Другими словами, 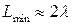 . Два важных случая нужно обсудить. Во-первых, для
. Два важных случая нужно обсудить. Во-первых, для 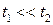 могут быть использованы приближения
могут быть использованы приближения 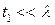 и
и 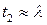 в уравнении (П1.7), чтобы получить
в уравнении (П1.7), чтобы получить 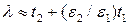 , что является приближением одной области на семинаре 1. Во-вторых, если
, что является приближением одной области на семинаре 1. Во-вторых, если 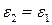 , наибольшее решение для
, наибольшее решение для  в (П1.7) есть просто
в (П1.7) есть просто 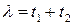 , полная физическая высота прямоугольного бокса на рис П1.1, как можно было и ожидать. В общем случае это позволяет интерпретировать
, полная физическая высота прямоугольного бокса на рис П1.1, как можно было и ожидать. В общем случае это позволяет интерпретировать  как диэлектрический эквивалент высоты полного бокса из двух областей, так что контроль ККЭ эквивалентен сохранению низкого аспектного отношения самого бокса.
как диэлектрический эквивалент высоты полного бокса из двух областей, так что контроль ККЭ эквивалентен сохранению низкого аспектного отношения самого бокса.
П1.2 Уравнение для характеристической длинымодели трех областей
Модель двух областей может быть распространена на структуру МОПТ с тремя областями, показанную на рис.П1.2. Следуя методу, изложенному выше, левые (исток) компоненты однородной части решения 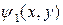 ,
, 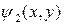 ,
, 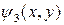 могут быть записаны как
могут быть записаны как
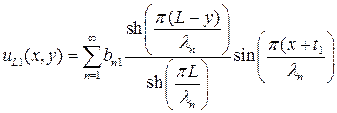 (П1.8)
(П1.8)
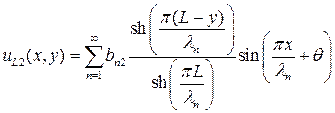 (П1.9)
(П1.9)
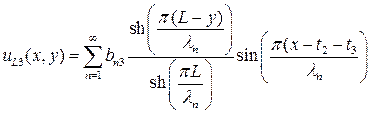 . (П1.10)
. (П1.10)
Заметим, что фаза синуса выбрана так, что 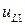 принимает нулевое значение на верхней границе, а
принимает нулевое значение на верхней границе, а 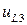 принимает нулевое значение на нижней границе. Фаза в
принимает нулевое значение на нижней границе. Фаза в 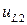 содержит дополнительную переменную
содержит дополнительную переменную 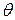 , определяемую позднее из граничных условий. Стоковые компоненты однородного решения могут быть выражены в форме, подобной выражениям (П1.2) и (П1.4). Они дают избыточные результаты, что касается уравнения для собственных значений.
, определяемую позднее из граничных условий. Стоковые компоненты однородного решения могут быть выражены в форме, подобной выражениям (П1.2) и (П1.4). Они дают избыточные результаты, что касается уравнения для собственных значений.
На границе между 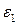 и
и 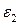 выполняются условия
выполняются условия 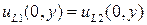 и
и 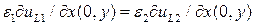 . Эти равенства к каждой паре соответствующих членов в двух рядах. Тогда их отношение дает
. Эти равенства к каждой паре соответствующих членов в двух рядах. Тогда их отношение дает
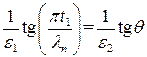 (П1.11)
(П1.11)
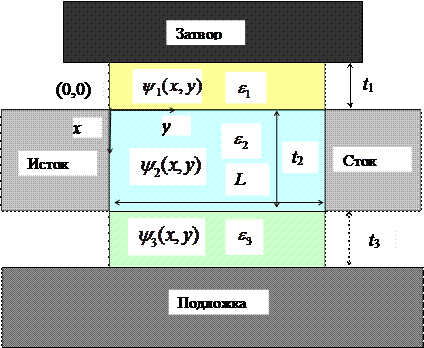
Рис.П1.2 Схематическая диаграмма МОПТ в модели трех областей.
На границе между 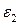 и
и 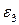 выполняются условия
выполняются условия 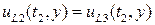 и
и 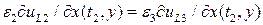 . Отношение соответствующих членов в двух рядах дает
. Отношение соответствующих членов в двух рядах дает
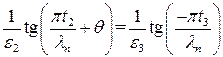 . (П1.12)
. (П1.12)
Исключая 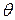 из выражений (П1.11) и (П1.12), получаем в результате уравнение собственных значений
из выражений (П1.11) и (П1.12), получаем в результате уравнение собственных значений  (или
(или  ) для трех областей
) для трех областей
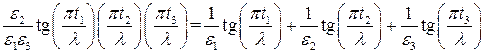 (П1.12)
(П1.12)
Решения есть 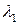 ,
, 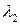 ,
, 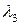 ,
, 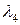 , в нисходящем порядке. Наибольшее собственное значение
, в нисходящем порядке. Наибольшее собственное значение 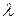 (используемое попеременно с
(используемое попеременно с 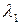 в лекциях и семинарах) есть эквивалентная длина масштабирования для трехслойной структуры на рис.П1.2. В специальном случае, когда
в лекциях и семинарах) есть эквивалентная длина масштабирования для трехслойной структуры на рис.П1.2. В специальном случае, когда 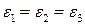 ,можно показать, что фундаментальное решение есть
,можно показать, что фундаментальное решение есть 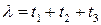 , как и ожидалось.
, как и ожидалось.
Модель характеристической длинытрех областей применима, например, для двухзатворных МОПТ и КНИ приборов с очень тонкими скрытыми слоями. Она может быть также применима в других случаях, замечая, что в то время как исток и сток предполагаются с диэлектрической постоянной 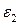 на рис П1.2, выражение (П1.13) равным образом справедливо, если исток и сток имеют диэлектрическую постоянную
на рис П1.2, выражение (П1.13) равным образом справедливо, если исток и сток имеют диэлектрическую постоянную 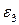 . Например, слой 3 может быть обедненной областью в объеме кремния, где находятся также исток и сток, и слои 1,2 представляют комбинированный изолятор затвора с различными диэлектрическими постоянными. В качестве альтернативы слой 2 может быть основанием изолятора затвора и слой 1 обедненной областью поликремниевого затвора.
. Например, слой 3 может быть обедненной областью в объеме кремния, где находятся также исток и сток, и слои 1,2 представляют комбинированный изолятор затвора с различными диэлектрическими постоянными. В качестве альтернативы слой 2 может быть основанием изолятора затвора и слой 1 обедненной областью поликремниевого затвора.



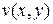 есть просто непрерывная линейная функция х для всей области
есть просто непрерывная линейная функция х для всей области 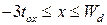 . Он также более точен, поскольку полное нижнее граничное условие
. Он также более точен, поскольку полное нижнее граничное условие 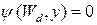 вдоль BE на рис.С1.4 удовлетворяется
вдоль BE на рис.С1.4 удовлетворяется 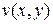 без необходимости для
без необходимости для 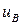 ряда. Результат подобен выражению (С1.27) с параметром а, замененным на m / 2. Так как в общем случае
ряда. Результат подобен выражению (С1.27) с параметром а, замененным на m / 2. Так как в общем случае 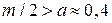 , экстремально ретроградно легированные МОПТ имеют слегка лучший ККЭ, чем в случае однородного легирования для тех же самых
, экстремально ретроградно легированные МОПТ имеют слегка лучший ККЭ, чем в случае однородного легирования для тех же самых 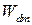 и
и 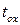 .
.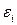 и толщиной
и толщиной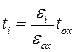 (С1.32)
(С1.32)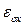 и толщиной
и толщиной 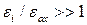 , физическая толщина high-k диэлектрика
, физическая толщина high-k диэлектрика 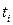 много больше, чем
много больше, чем 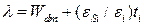 для high-k диэлектриков. Однако это справедливо только для
для high-k диэлектриков. Однако это справедливо только для 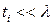 , когда преобладают нормальные (вертикальные) поля. Когда возрастают и
, когда преобладают нормальные (вертикальные) поля. Когда возрастают и 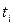 с одинаковым коэффициентом, то есть при постоянной емкости
с одинаковым коэффициентом, то есть при постоянной емкости 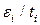 , продольные поля становятся более важными, поскольку высокая диэлектрическая постоянная их не улучшает. При произвольных диэлектрической постоянной и толщине необходимо использовать обобщенную модель двух областей для длины масштабирования, описанную в Приложении 1. При согласовании граничных условий для нормальных и тангенциальных полей на границе кремний-диэлектрик, собственные значения характеристической длиныполучаются из уравнения:
, продольные поля становятся более важными, поскольку высокая диэлектрическая постоянная их не улучшает. При произвольных диэлектрической постоянной и толщине необходимо использовать обобщенную модель двух областей для длины масштабирования, описанную в Приложении 1. При согласовании граничных условий для нормальных и тангенциальных полей на границе кремний-диэлектрик, собственные значения характеристической длиныполучаются из уравнения: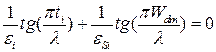 . (С1.33)
. (С1.33)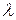 . Наименьшая степень собственного значения, или наименьшее
. Наименьшая степень собственного значения, или наименьшее 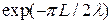 , как и в модели одной области. Уравнение (С1.33) не может быть решено аналитически. Численное решение для наибольших
, как и в модели одной области. Уравнение (С1.33) не может быть решено аналитически. Численное решение для наибольших 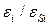 .
.
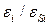 . Пунктирные линии в правом нижнем углу показывают поведение асимптотического решения
. Пунктирные линии в правом нижнем углу показывают поведение асимптотического решения 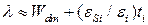 для
для 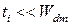 [3].
[3]. остается прежней: она предписывает минимальную длину канала,
остается прежней: она предписывает минимальную длину канала, 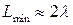 , как предсказывалось с модели одной области, обсуждавшейся выше.
, как предсказывалось с модели одной области, обсуждавшейся выше.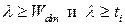 , если
, если 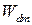 ,
, 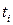 .
.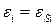 ,
, 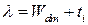 , физической высоте в боксе на
, физической высоте в боксе на 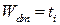 ,
, 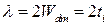 , независимо от
, независимо от 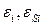 .
.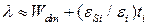 . Это приближенное решение получается в модели одной области.
. Это приближенное решение получается в модели одной области.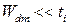 (верхний левый угол на рис.3.26),
(верхний левый угол на рис.3.26), 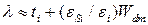 .
.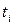 и
и 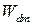 , анализ
, анализ 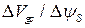 или m -фактора требуют, чтобы
или m -фактора требуют, чтобы 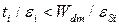 . Другими словами, для
. Другими словами, для 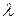 приемлемо только решение в нижнем правом углу рис.С1.6.. В этой области high-k диэлектрик помогает, так как
приемлемо только решение в нижнем правом углу рис.С1.6.. В этой области high-k диэлектрик помогает, так как 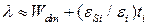 , и для того же самого
, и для того же самого 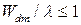 более высокое
более высокое 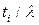 . Однако, вследствие чрезвычайной нелинейности кривой для
. Однако, вследствие чрезвычайной нелинейности кривой для 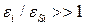 решение для
решение для 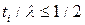 или
или 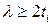 , где
, где 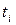 − физическая толщина изолятора независимо от того, как велика его диэлектрическая постоянная. Физически это обусловлено продольными полями, в отличие от вертикальных полей, не затрагиваемых диэлектрической константой материала. В приборах с очень толстым и с очень высокой диэлектрической константой high-k диэлектриком доминируют продольные поля, так что характеристическая длинаопределяется главным образом физической толщиной пленки.
− физическая толщина изолятора независимо от того, как велика его диэлектрическая постоянная. Физически это обусловлено продольными полями, в отличие от вертикальных полей, не затрагиваемых диэлектрической константой материала. В приборах с очень толстым и с очень высокой диэлектрической константой high-k диэлектриком доминируют продольные поля, так что характеристическая длинаопределяется главным образом физической толщиной пленки.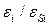 <1, то есть SiO2, кривизна кривой на рис.С1.6. противоположна той, что при
<1, то есть SiO2, кривизна кривой на рис.С1.6. противоположна той, что при 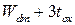 , так как
, так как 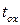 увеличивается.
увеличивается.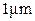 channel CMOS technology with retrograde n-well and thin epitaxy, IEEE Trans. Electron Devices ED-32, 203-209.
channel CMOS technology with retrograde n-well and thin epitaxy, IEEE Trans. Electron Devices ED-32, 203-209.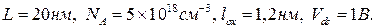
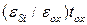 или
или 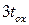 . Как указывалось, это корректно определяет нормальное поле (
. Как указывалось, это корректно определяет нормальное поле (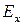 ), но тангенциальное поле (
), но тангенциальное поле (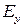 ) – некорректно. Модель одной области справедлива, только если толщина окисла много тоньше, чем характеристическая длина
) – некорректно. Модель одной области справедлива, только если толщина окисла много тоньше, чем характеристическая длина 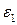 и толщину t 1. Обедненная область полупроводника имеет диэлектрическую проницаемость
и толщину t 1. Обедненная область полупроводника имеет диэлектрическую проницаемость 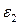 и толщину t 2. Заметим, что нижняя граница обедненной области упрощена до прямой линии тем же образом, как на рис.С1.4. В подпороговой области пренебрегается подвижными носителями в инверсной области. Электрический потенциал находится из решения двумерного уравнения Пуассона, примененного к прямоугольной области на рис П1.1.Существует проблема граничного условия, в которой требуется точно определить потенциал на четырех проводящих сторонах прямоугольника, левой (исток), верхней (затвор), правой (сток), нижней (подложка). Имеется реально два малых зазора, не огороженных проводниками: наверху слева между затвором и истоком и наверху справа между затвором и стоком. Когда эти зазоры не чрезмерно велики (по сравнению с, например,
и толщину t 2. Заметим, что нижняя граница обедненной области упрощена до прямой линии тем же образом, как на рис.С1.4. В подпороговой области пренебрегается подвижными носителями в инверсной области. Электрический потенциал находится из решения двумерного уравнения Пуассона, примененного к прямоугольной области на рис П1.1.Существует проблема граничного условия, в которой требуется точно определить потенциал на четырех проводящих сторонах прямоугольника, левой (исток), верхней (затвор), правой (сток), нижней (подложка). Имеется реально два малых зазора, не огороженных проводниками: наверху слева между затвором и истоком и наверху справа между затвором и стоком. Когда эти зазоры не чрезмерно велики (по сравнению с, например,  Используя тот же метод суперпозиции, что и в семинаре 1, решение для потенциала внутри выделенных областей,
Используя тот же метод суперпозиции, что и в семинаре 1, решение для потенциала внутри выделенных областей, 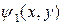 для области 1 и
для области 1 и 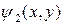 для области 2, может быть разложено на несколько компонент.
для области 2, может быть разложено на несколько компонент.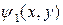 могут быть записаны как
могут быть записаны как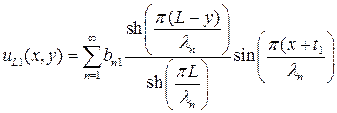 (П1.1)
(П1.1)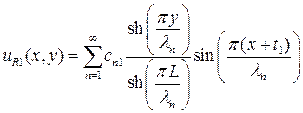 (П1.2)
(П1.2)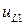 и
и 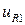 удовлетворяет уравнению Лапласа, например,
удовлетворяет уравнению Лапласа, например, 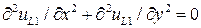 для любого
для любого  . Также заметим, что
. Также заметим, что 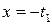 ) и правой (
) и правой (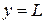 ) границах, в то время как
) границах, в то время как 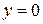 ) границах. Подобным же образом, левая и правая компоненты
) границах. Подобным же образом, левая и правая компоненты 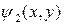 равны
равны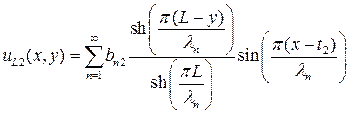 (П1.3)
(П1.3)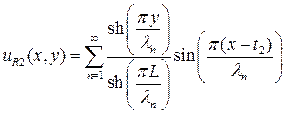 , (П1.4)
, (П1.4)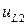 принимает нулевое значение на нижней (
принимает нулевое значение на нижней (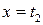 ) и правой (
) и правой (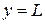 ) границах, в то время как
) границах, в то время как 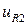 принимает нулевое значение на нижней и левой (
принимает нулевое значение на нижней и левой (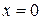 , при нормальном перемещении через границу величина
, при нормальном перемещении через границу величина 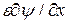 , также как потенциал
, также как потенциал 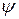 (следовательно, тангенциальное поле,
(следовательно, тангенциальное поле, 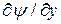 ) должны быть непрерывны при переходе из одной диэлектрической среды в другую. Вследствие различия формы функций от у, каждый член в
) должны быть непрерывны при переходе из одной диэлектрической среды в другую. Вследствие различия формы функций от у, каждый член в 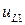 и
и 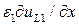 должен быть равен их аналогу в
должен быть равен их аналогу в 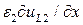 при
при 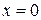 . Следовательно, получаем
. Следовательно, получаем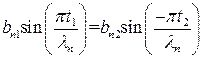 (П1.5)
(П1.5)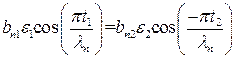 . (П1.6)
. (П1.6)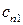 и
и 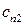 из
из 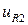 и их производных. Для ненулевых решений
и их производных. Для ненулевых решений 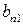 и
и 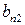 выражения (П1.5) и (П1.6) могут быть поделены друг на друга, чтобы получить уравнение для собственных значений
выражения (П1.5) и (П1.6) могут быть поделены друг на друга, чтобы получить уравнение для собственных значений 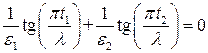 . (П1.7)
. (П1.7)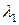 ,
, 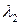 ,
, 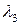 ,
, 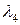 , в нисходящем порядке. Наибольшее собственное значение является и наиболее важным, так как каждый член короткоканального вклада в потенциал пропорционален
, в нисходящем порядке. Наибольшее собственное значение является и наиболее важным, так как каждый член короткоканального вклада в потенциал пропорционален  [смотри семинар 1, например, выражение (С1.26)]. В полной короткоканальной части потенциала доминирует член с наибольшим
[смотри семинар 1, например, выражение (С1.26)]. В полной короткоканальной части потенциала доминирует член с наибольшим 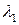 . Члены более высокого порядка в выражениях (П1.1) - (П1.4) пренебрежимо малы при условии, что длина канала не сравнима или короче, чем
. Члены более высокого порядка в выражениях (П1.1) - (П1.4) пренебрежимо малы при условии, что длина канала не сравнима или короче, чем 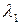 .
.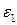 ,
, 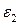 ,
, 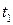 ,
, 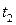 уравнение (П1.7) может бать решено относительно характеристической длины
уравнение (П1.7) может бать решено относительно характеристической длины 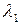 ), которая является эквивалентом двух областей вместо
), которая является эквивалентом двух областей вместо 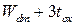 . ККЭ приемлемы, если
. ККЭ приемлемы, если 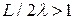 . Другими словами,
. Другими словами, 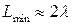 . Два важных случая нужно обсудить. Во-первых, для
. Два важных случая нужно обсудить. Во-первых, для 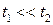 могут быть использованы приближения
могут быть использованы приближения 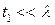 и
и 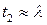 в уравнении (П1.7), чтобы получить
в уравнении (П1.7), чтобы получить 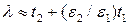 , что является приближением одной области на семинаре 1. Во-вторых, если
, что является приближением одной области на семинаре 1. Во-вторых, если 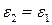 , наибольшее решение для
, наибольшее решение для 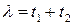 , полная физическая высота прямоугольного бокса на рис П1.1, как можно было и ожидать. В общем случае это позволяет интерпретировать
, полная физическая высота прямоугольного бокса на рис П1.1, как можно было и ожидать. В общем случае это позволяет интерпретировать 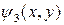 могут быть записаны как
могут быть записаны как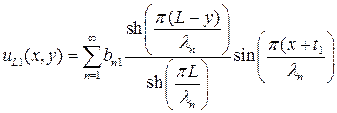 (П1.8)
(П1.8)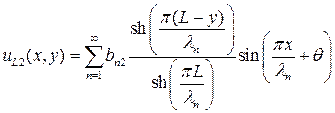 (П1.9)
(П1.9)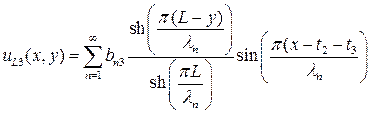 . (П1.10)
. (П1.10)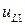 принимает нулевое значение на верхней границе, а
принимает нулевое значение на верхней границе, а 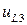 принимает нулевое значение на нижней границе. Фаза в
принимает нулевое значение на нижней границе. Фаза в 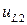 содержит дополнительную переменную
содержит дополнительную переменную 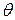 , определяемую позднее из граничных условий. Стоковые компоненты однородного решения могут быть выражены в форме, подобной выражениям (П1.2) и (П1.4). Они дают избыточные результаты, что касается уравнения для собственных значений.
, определяемую позднее из граничных условий. Стоковые компоненты однородного решения могут быть выражены в форме, подобной выражениям (П1.2) и (П1.4). Они дают избыточные результаты, что касается уравнения для собственных значений.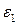 и
и 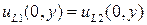 и
и 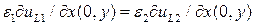 . Эти равенства к каждой паре соответствующих членов в двух рядах. Тогда их отношение дает
. Эти равенства к каждой паре соответствующих членов в двух рядах. Тогда их отношение дает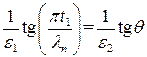 (П1.11)
(П1.11)
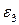 выполняются условия
выполняются условия 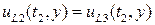 и
и 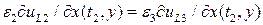 . Отношение соответствующих членов в двух рядах дает
. Отношение соответствующих членов в двух рядах дает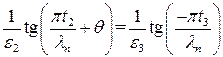 . (П1.12)
. (П1.12)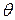 из выражений (П1.11) и (П1.12), получаем в результате уравнение собственных значений
из выражений (П1.11) и (П1.12), получаем в результате уравнение собственных значений 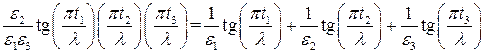 (П1.12)
(П1.12)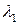 ,
, 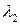 ,
, 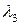 ,
, 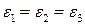 ,можно показать, что фундаментальное решение есть
,можно показать, что фундаментальное решение есть 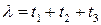 , как и ожидалось.
, как и ожидалось.


