В терминах системного подхода, ТП и комплекс условий, в которых он движется, представляет собой типичный пример сложной системы (СС). Под СС понимают большое количество взаимно связанных и взаимодействующих между собой элементов, организованных таким образом, чтобы наиболее эффективно достичь поставленной цели. При разработке проблемы, связанной с движением ТП следует рассматривать СС «водитель – средства управления автомобилем – автомобиль – дорога – средства организации движения – среда». Особенностью этой системы является функционирование в условиях действия большого количества случайных факторов.
В настоящее время однозначного, четкого определения сложной системы нет. Известны различные подходы и предложены различные формальные признаки ее определения. Так, советский ученый Г.Н. Поворов предлагает относить к сложным системы имеющие 104-107 элементов; к ультросложным - системы, состоящие из 107-1030 элементов; и к суперсистемам – системы из 1030-10200 элементов.
Такой подход имеет тот недостаток, что данное определение сложности является относительным, а не абсолютным.
Английский кибернетик С. Бир предлагает к сложным относить системы, описываемые на языке теоретико-вероятностных методов (мозг, экономика, форма и т.п.).
Наиболее четким определением сложных систем является определение: Сложной системой называется система, в модели которой недостаточно информации для эффективного управления этой системой.
Таким образом, признаком простоты системы является достаточность информации для ее управления. Если же результат управления, полученный с помощью модели, будет неожиданным, то такую систему относят к сложной.
От сложных систем необходимо отличать большие системы.
Система, для моделирования которой в целях управления недостает материальных ресурсов (машинного времени, емкости памяти, других материальных средств моделирования) называется большой.
К таким системам относятся экономические, организационно-управленческие, нейрофизиологические, биологические и т.п. системы.
Способом перевода больших систем в простые является создание новых более мощных средств вычислительной техники.
Движение ТП является результатом непрерывного взаимодействия между отдельными элементами системы, как в пространстве, так и во времени. Подсистемами ТП как СС могут быть: подсистема потока автомобилей, подсистемы дорожных условий и средств организации движения, подсистемы управления автомобилем и т.д. (рис.1). Каждая из этих подсистем также является СС, требующей применения тех же методов анализа и оценки функционирования, как вся сложная система «В-СУА-А-Д-СОД-С».
Чтобы обеспечить наиболее эффективное функционирование системы, т.е. наиболее безопасные, удобные и экономичные условия ДД, необходимо определить количественные связи внутри системы (построить модель структуры) и установить их влияние на поведение всей системы как единого целого – выявить интегративные (эмерджентные) свойства.
Основная концепция системного подхода – это представление исследуемого объекта или процесса в виде системы S и ее последующий анализ с целью выявления основных закономерностей функционирования. Этапы методики системного подхода: формулировка целей функционирования, выделение системы из среды ее функционирования, моделирование, разработка структуры системы управления, обеспечивающей достижение заданных целей.
Система, по В.Н. Согатовскому, – это «конечное множество функциональных элементов A и отношений между ними R, выделенное из среды SR в соответствии с определенной целью Z в рамках определенного временного интервала DT».
Sº<A, R, Z, SR, DT> (1.1)
Для описания ТП как СС могут быть использованы: теория вероятностей, математическая статистика, вычислительная техника, теория массового обслуживания, теория игр, линейное программирование, моделирование, теория информации и психофизиология человека [4].

Рисунок 1.2 ДД как СС
Известные и нашедшие практическое применение ММ в ОДД можно разделить на две группы: детерминированные и стохастические.

Рисунок 1.3 Модели ТП
К детерминированным (динамическим) относятся модели, в основу которых заложена функциональная зависимость между отдельными показателями ТП, например, связь между скоростью и дистанцией, интенсивностью и скоростью и т.д. В случаях, часто наблюдаемых в большом городе или на скоростной дороге, когда много автомобилей движутся в группе, транспортный поток может быть рассмотрен как детерминированный и непрерывный. Таким образом, с помощью детерминированных моделей исследуют ТП высокой плотности, в которых автомобили находятся в тесном взаимодействии между собой и решающую роль играет человек как оператор.
Стохастические (вероятностные) модели рассматривают ТП как вероятностный, случайный процесс, например, распределение интервалов между автомобилями в ТП может приниматься не строго определенным, а случайным. ТП, движущийся по УДС, состоит из множества автомобилей, которые управляются по более или менее свободному желанию водителей, и маневры каждого автомобиля могут быть расценены как вероятностные события. Таким образом, с помощью стохастических моделей исследуют ТП низкой плотности.
Если обсуждаются условия, влияющие на безопасность движения на дороге, или стартовые характеристики автомобилей, начинающих движение от регулируемого перекрестка, то следует использовать вероятностный подход и микроскопические модели, которые представляют движение отдельных автомобилей. C другой стороны, имея дело с ТП, движущимся по УДС, оборудованных множеством регулируемых перекрестков, возможно, что выгоднее пользоваться макроскопической моделью, которая отображает ТП как стационарное явление, представляемое общей средней скоростью, плотностью потока и интенсивностью, поскольку микроскопическая модель слишком детальна для представления потоков с высокой плотностью.
Вопросы для повторения
- Что такое сложная система?
- Почему ТП относят к СС?
- В чем состоит основная концепция системного подхода?
- Какие элементы включает система по Согатовскому?
- Перечислите основные виды математических моделей ТП.
- Чем детерминированные модели ТП отличаются от стохастических?
- В каких случаях используют макроскопические модели, а в каких микроскопические?
Макроскопические модели ТП
Макроскопические модели рассматривают ТП как сплошную среду, состоящую из большого количества близко расположенных друг к другу автомобилей. Для математического описания состояния движущегося ТП как сплошной среды необходимо использовать следующие основные законы: уравнение состояния потока автомобилей, уравнение неразрывности, закон сохранения количества движения, закон сохранения энергии. Процессы, происходящие внутри ТП, не могут быть исследованы с помощью данной теории. Основное практическое значение имеет анализ волнового движения ТП с точки зрения выявления степени влияния препятствий.
Макроскопическая модель ТП определяется как модель, представляющая средние характеристики ТП (средняя скорость v, плотность q и интенсивность N), состоящего из автомобилей, каждый из которых имеет стохастические характеристики.
Под уравнением состояния ТП как сплошной среды понимают следующее уравнение:
 . (1.2)
. (1.2)
Получим уравнение неразрывности ТП, основанное на принципах закона сохранения масс. Анализируя ТП, рассматривается постоянство общего числа автомобилей во времени dK/dt=0. Изменение общего числа автомобилей на участке дороги dx за время dt может происходить как в результате изменения плотности q, так и в результате изменения интенсивности N.
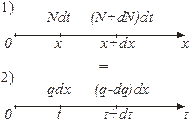
Рисунок 1.4
Если рассматривать ТП как стационарную систему, то изменение между числом автомобилей по длине дороги dx за время dt должно быть равно разности между числом автомобилей входящих на участок x и числом автомобилей, выходящих с участка x+dx.
Пусть x – расстояние вдоль дороги. Рассмотрим бесконечно малый участок дороги dx. Изменение количества автомобилей dK за время dt может быть найдено как разность между прибывающими автомобилями в точку x и убывающими из точки x+dx.
 , (1.3)
, (1.3)
где dN – бесконечно малое изменение интенсивности на участке dx.
С другой стороны изменение количества автомобилей dK можно выразить через изменение плотности q за время dt.
 . (1.4)
. (1.4)
Приравняем выражения (1.3) и (1.4)
 , (1.5)
, (1.5)
и получим «закон сохранения автомобилей»
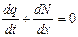 , (1.6)
, (1.6)
выведенный при условии, что на участке дороги нет въездов и съездов. Смысл этого уравнения следующий: количество автомобилей, входящих в момент времени dt на участок dx, равно количеству автомобилей, выходящих с этого участка.
Рассмотрим связь между характеристиками ТП: скоростью v плотностью q. Получим уравнение движения ТП.
Будем считать, что скорость v в точке x определяется только плотностью q в x: 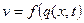 . Определим v’ как:
. Определим v’ как:
 . (1.7)
. (1.7)
Примем среднее ускорение наблюдателя таким, какое обычно имеет патрульный автомобиль дорожной службы, двигающийся со скоростью, равной средней скорости потока v.
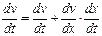 . (1.8)
. (1.8)
Выполним следующие преобразования
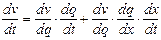 . (1.9)
. (1.9)
С учетом (1.6.6) получим:
 . (1.10)
. (1.10)
Учитывая, что N=ν*ϥ и с учетом выражения (1.6), а также пользуясь правилами дифференцирования произведения, получим
 . (1.11)
. (1.11)
Подставим (1.11) в выражение (1.10) и получим уравнение движения ТП
 , (1.12)
, (1.12)
где отрицательный коэффициент  можно интерпретировать, как коэффициент трения в случае динамики жидкостей. Для классической сжимаемой жидкости уравнение (1.12) носит название уравнения движения и имеет вид:
можно интерпретировать, как коэффициент трения в случае динамики жидкостей. Для классической сжимаемой жидкости уравнение (1.12) носит название уравнения движения и имеет вид:
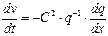 , (1.13)
, (1.13)
где С – неотрицательная константа с размерностью скорости.
Однако гипотеза о рассмотрении ТП аналогично классической жидкости излишне груба и следует рассматривать более общий класс моделей, таких как:
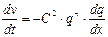 . (1.14)
. (1.14)
Уравнение (1.13) соответствует случаю, когда n=-1, следовательно, мы предполагаем, что
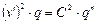 . (1.15)
. (1.15)
Учитывая (1.7), выразим 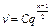 , выполним разделение переменных и проинтегрируем
, выполним разделение переменных и проинтегрируем
 . (1.16)
. (1.16)
Следует отметить, что при n=-1 (15) имеет вид
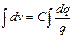 . (1.17)
. (1.17)
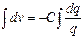
 начальные условия q=qmax, при v=0
начальные условия q=qmax, при v=0

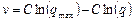

| 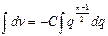 ; ;  начальные условия q=qmax, при v=0
начальные условия q=qmax, при v=0
 ; ; 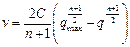
|
Приведенные уравнения имеют следующие решения:
при n=-1
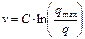 , (1.18)
, (1.18)
при n¹-1
 , (1.19)
, (1.19)
где qmax – максимально возможная плотность ТП на дороге, при которой v=0.
Модель, выраженная уравнением (1.18) была впервые получена Гринбергом в 1959 г. Результаты расчетов по данной модели достаточно хорошо сходятся с экспериментальными данными для плотностей потока отличных от нуля (рис. 1.6).
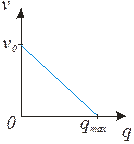
Рисунок 1.5 Приближенная связь между v и q
(модель Гриншильдса)
Для модели с n³0 обозначим через v0 скорость при q=0:

Рисунок 1.6. Модель Гринберга и экспериментальные данные
 (1.20)
(1.20)
Модель, представленная на рис. 1.5, получается, как частный случай из уравнения (1.20), при n=1 (линейно зависит от q) и называется моделью Гриншильдса, которая впервые была получена в 1934 г.
Рассмотрим взаимосвязь между v, q, N. Подставим N=q×v в уравнения (1.18) и (1.20) и получим:
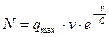 . (1.21)
. (1.21)
 . (1.22)
. (1.22)
 (1.23)
(1.23)
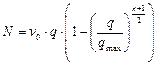 (1.24)
(1.24)

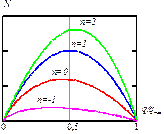
Рисунок 1.7 Влияние параметра n на вид модели
Величина скорости v1 и плотности q1, которые максимизируют интенсивность потока N, могут быть получены путем дифференцирования вышеприведенных моделей (1.23), (1.24) и даны ниже:
n=-1 (модель Гринберга) v1=C, q1=qmax/e, Nmax=C×qmax/e;
n=1 (модель Гриншильдса) v1=v0/2, q1=qmax/2, Nmax= v0×qmax/4;
n¹-1 (обобщенная модель) v1=(n+1)v0/(n+3), q1=qmax((n+3)/2)2/(n+1),
Nmax= v0×qmax((n+1)/(1/22/n+1(n+3)2/(n+1)+1));
Рассмотрим уравнение сохранения количества движения. При движении ТП по аналогии с движением жидкости количество движения характеризуется величиной qv. Данное уравнение получается умножением на v уравнения неразрывности (1.6.5) и умножением на q уравнения движения (1.6.13). Затем, складывая полученные уравнения, получаем уравнение сохранения количества движения.
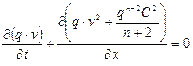 . (1.25)
. (1.25)
Рассмотрим уравнение, характеризующее энергетическое состояние ТП. Общее энергетическое состояние ТП, пользуясь гидродинамической аналогией, можно характеризовать суммой кинетической Ek и внутренней U энергии.
E=Ek + U (1.26)
Уравнение (1.26) является законом сохранения энергии ТП. При этом кинетическая энергия ТП определяется как:
Ek=gqv2, (1.27)
где g - постоянная.
Внутренняя энергия характеризует степень устойчивости движения ТП, от которой зависит величина этой энергии. Потеря внутренней энергии может быть вызвана неблагоприятными дорожными условиями или увеличением плотности потока. Величиной внутренней энергии считают среднеквадратичную величину ускорения движения автомобилей sа на участке дороги S.
E=gqv2 + sа. (1.28)
Граничными условиями закона являются:
при v®0,
E=gqmaxv2max; (1.29)
при Ek®0,
Е=(sа)max. (1.30)
Исходя из граничных условий (26) получим g как
g=(sа)max/(qmaxv2max). (1.31)
Таким образом, уравнение (1.27) примет окончательный вид:
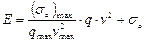 . (1.32)
. (1.32)
Основная диаграмма ТП. Основные уравнения движения ТП как сплошной среды можно использовать для анализа возникновения волн в потоке, вызывающих качественные изменения в нем. Скорость распространения кинематической волны определяют с помощью основной диаграммы ТП.

Рисунок 1.8 Основная диаграмма ТП
При этом средняя скорость vcp движения ТП и мгновенная скорость vм будут определяться как:
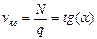 (1.33)
(1.33)
 (1.34)
(1.34)
Скорость распространения кинематической волны vм равна тангенсу угла наклона к оси х касательной к кривой N(q). С увеличением плотности q угол наклона b касательной уменьшается, вызывая уменьшение скорости потока vср. Как следует из уравнения (1.34) величина vм принимает меньшие значения, чем vср при условии отрицательного отношения dv/dq. Скорости vм и vср принимают равные значения только при интенсивности, при которой начинает сказываться взаимное влияние автомобилей в ТП. В этой точке кривой N(q) отношение dv/dq=0.
Рассматриваемые волны можно назвать волнами изменения интенсивности ТП по длине дороги. При максимальной интенсивности движения, соответствующей пропускной способности, возникает стационарная волна. Наложение более быстрых волн на более медленные, приводит к образованию ударной волны.
Ударные волны в ТП. Рассмотрение макроскопической модели ТП показывает, что в ней, т.е. на кривых N(v) существуют области неустойчивости. Получим уравнение в приращениях для модели Гриншильдса (n=1), путем придания приращения Dv, отбрасывания составляющих второго порядка и составляющих не содержащих Dv:
 . (1.35)
. (1.35)

Рисунок 1.9 Влияние положительной обратной связи (ПОС)

Рисунок 1.10 Движение границ плотности ТП
Считаем что скорость vÎ[0, v0] и dv/dq>0, тогда если по любой причине скорость некоторой части потока понизится на Dv, то интенсивность N, в соответствии с (1.35) понизится на DN. Следовательно, плотность этой части потока повысится, и скорость дальше будет снижаться. Таким образом, вследствие воздействия контура положительной обратной связи, возмущение скорости является незатухающим, что и демонстрирует неустойчивость поведения ТП. В этих случаях автомобили вынуждены неоднократно трогаться с места и останавливаться. Такое явление носит название ударная волна.
Как показано на рис. 1.10 примем, что плотности соседних участков 1 и 2 дороги различны, и обозначим плотность и скорость движения через q1, q2 и v1, v2. Если С – скорость движущейся границы между 1 и 2, то исходя из уравнения неразрывности (5), имеем:
 (1.36)
(1.36)
Решая уравнение относительно С, получим:
 (1.37)
(1.37)
В случае малых изменений плотности q мы можем легко получить скорость с передвижения граничной точки из уравнения (1.37) т.е. с=dN/dq. Учитывая уравнение состояния ТП, получим:
 . (1.38)
. (1.38)
Например, для модели Гриншильдса (соотношения (1.23), (1.24) при n=1) величины с и С определяют по формулам:
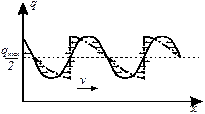
Рисунок 1.11 Образование ударной волны
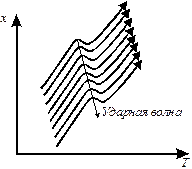
Рисунок 1.12 Ударная волна

. 1.39)
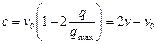 . (1.40)
. (1.40)
Из уравнения (1.40) следует, что скорость граничной точки с при пренебрежимо малом изменении q (или v) удовлетворяет условиям:
 (1.41)
(1.41)
Таким образом, в ТП, показанном сплошной линией на рис. 1.11, часть волны над линией q=qmax/2 будет двигаться назад против потока, а часть волны ниже линии – вперед в направлении потока. Поэтому исходная форма волны транспортного потока изменяется и в пределе приобретает форму, показанную пунктиром, при которой существуют резкие изменения в плотности. Эта точка разрыва плотности называется ударным фронтом ТП, который после образования движется со скоростью, определяемой уравнением (31). Когда образуется ударная волна, автомобили начинают вести себя в соответствии с рис. 1.12 и вынуждены замедлять скорость или останавливаться.
Вопросы для повторения
1. Перечислите основные уравнения транспортного потока при описании его на макроуровне.
2. Постройте график зависимости плотности от скорости ТП для модели Гриншилдса.
3. Запишите зависимость интенсивности от плотности потока для модели Гринберга.
4. Как из обобщенной модели ТП получить модели Гриншилдса и Гринберга?
5. Запишите уравнение состояния ТП.
6. В чем суть уравнения неразрывности ТП?
7. Что такое основная диаграмма ТП? Изобразите график основной диаграммы ТП.
8. Какие характеристики можно вычислить, пользуясь основной диаграммой ТП?
Микроскопические модели ТП
При учете взаимодействия между автомобилями возникают задачи установления закономерностей режима движения одиночных автомобилей и механизма передачи воздействия автомобилей друг на друга. При этом необходимо детально рассматривать систему «водитель-автомобиль», основным регулятором которой является человек. При разработке теоретических моделей движения плотных ТП учитывают показатели, характеризующие действия водителей. На основе изучения взаимодействия между автомобилями можно определить такие общие характеристики, как пропускная способность, средняя скорость, плотность. Данная теория особенно эффективна при решении задач, связанных со сравнительно короткими участками дорог.
Дистанция между автомобилями является основным параметром, зависящим от действий водителя при взаимодействии в плотном ТП. Первые динамические теории ТП строились на гипотезе о существовании определенной закономерности взаимодействия автомобилей, движущихся друг за другом на близком расстоянии, и позволяли определять среднюю дистанцию между автомобилями при различных скоростях движения.
Развитием теории упрощенных динамических моделей является теория «следования за лидером», основанная на гипотезе о существовании определенной закономерности взаимодействия автомобилей, движущихся друг за другом на близком расстоянии. Дифференциальное уравнение теории «следования за лидером» получено исходя из предпосылки, что все автомобили движутся в колонне на расстоянии, требуемом правилами дорожного движения.

Рисунок 1.13 Координаты положения автомобилей при движении в колонне
Из рис. 1.13 видно, что при соблюдении требований правил движения положения n-ного и (n+1) автомобилей можно выразить зависимостью:
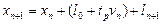 , (1.42)
, (1.42)
где l0 – минимальное расстояние между стоящими автомобилями, tpvn – расстояния между автомобилями, устанавливаемые в зависимости от скорости движения, ln+1 – длина автомобиля, n – порядковый номер автомобиля.
Дифференцируя (1.42) по времени получим:
 , (1.43)
, (1.43)
где n=1, 2, 3…N.
Выразим соотношение (1.43) через скорость v следующим образом:
 (1.44)
(1.44)
или
 , (1.45)
, (1.45)
где dvn/dt – ускорение заднего автомобиля, vn и vn+1 – скорости заднего и переднего автомобилей, a=1/tp, tp – продолжительность реакции.
Уравнение (1.45) является первым дифференциальным уравнением теории «следования за лидером» (или линейной теории «следования за лидером») и формулируется следующим образом: при следовании двух автомобилей друг за другом на достаточно близком расстоянии, когда сказывается их взаимное влияние, ускорение заднего автомобиля прямо пропорционально разности скоростей переднего и заднего автомобилей (относительной скорости). Коэффициент a называют чувствительностью водителя.
Следует отметить, что на практике коэффициент a не является постоянной величиной, а принимает меньшие значения при появлении больших величин пространственных интервалов по отношению к автомобилю лидеру и большие значения при высоких скоростях. Кроме того, чувствительность зависит от скорости автомобиля, чем скорость движения выше, тем чувствительность также становится выше. С этой точки зрения преобразуем уравнение (1.45) к виду:
 . (1.46)
. (1.46)
Соотношение (1.45) является вторым уравнением теории «следования за лидером» (нелинейная теория «следования за лидером») и формулируется следующим образом: «ускорение заднего автомобиля прямо пропорционально разности скоростей переднего и заднего автомобиля и обратно пропорционально расстоянию между ними».
На основании соотношений (1.45) и (1.46) запишем обобщенное уравнение теории «следования за лидером»:
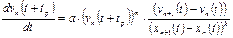 , (1.47)
, (1.47)
где а – постоянная, m, k – показатели степени.
В простейшем случае m=0, k=1, соотношение (1.47) примет вид:
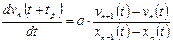 . (1.48)
. (1.48)
Проинтегрируем уравнение (1.48), путем выполнения разделения переменных и выполнения следующих преобразований:
 . (1.49)
. (1.49)
 . (1.50)
. (1.50)
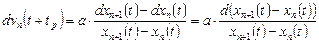 . (1.51)
. (1.51)
После интегрирования (1.51) получим:
 , (1.52)
, (1.52)
где С – постоянная интегрирования.
Дальнейшее преобразование (1.52) даст нам следующую зависимость:
 . (1.53)
. (1.53)
Когда ТП является стационарным, то плотность q выражается следующим соотношением:
 . (1.54)
. (1.54)
Учитывая (1.54) и то, что скорость v в стационарном режиме постоянна, то получим:
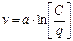 . (1.55)
. (1.55)
Выражение (1.55) идентично уравнению (1.22), и мы из микроскопической модели «следования за лидером» получаем макроскопическую модель Гринберга.
Основные выводы и общая оценка детерминированных моделей ТП.
Условия гидродинамической теории предполагают существование однородного ТП, состоящего из автомобилей одного типа. Однако на практике такие потоки наблюдаются редко. С практической точки зрения наиболее реальной является ТСЛ, которая описывает взаимодействие между автомобилями и учитывает психофизиологические особенности водителей.
Несмотря на различные начальные модели, все детерминированные (динамические) теории тесно связаны между собой. Теоретические исследования показывают, что решение уравнений ТСЛ приводит к конечному уравнению гидродинамической теории. Кроме того, с помощью каждой из детерминированных теорий можно построить основную диаграмму движения ТП «интенсивность-плотность», в которой связаны между собой характеристики движения ТП.
По диаграмме «N-q» можно определить все характеристики движения ТП: скорость, плотность, интенсивность, скорость распространения ударной волны и т.п.
Часть кривой расположенная слева от линии 0,5 соответствует нормальным условиям движения без образования заторов, правая часть кривой – движению автомобилей при возникновении заторов.

Рисунок 1.14 Основная диаграмма ТП
Максимальная интенсивность, получаемая по диаграмме соответствует пропускной способности рассматриваемого участка дороги. По основной диаграмме можно определить среднюю скорость ТП и скорость распространения кинематической волны в ТП.
Кроме того, из основной диаграммы ТП можно оценить среднюю величину интервала во времени между следующими друг за другом автомобилями Dt и интервала во времени между заднем бампером переднего автомобиля и передним бампером заднего автомобиля dt.
Общий вид уравнения «N-q», полученный на основе теории следования за лидером следующий
 (1.56)
(1.56)
Таким образом, результаты, полученные по различным теориям совпадают.
Вопросы для повторения
1. Для решения каких задач применяют микроскопические модели ТП?
2. В чем состоит основная гипотеза МСЛ?
3. Что описывает первое дифференциальное уравнение ТСЛ?
4. Запишите и объясните смысл второго уравнения ТСЛ?
5. Какие результаты дают детерминированные модели ТП?





 . (1.2)
. (1.2)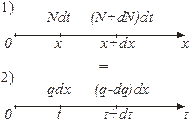
 , (1.3)
, (1.3) . (1.4)
. (1.4) , (1.5)
, (1.5)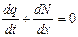 , (1.6)
, (1.6)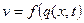 . Определим v’ как:
. Определим v’ как: . (1.7)
. (1.7)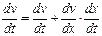 . (1.8)
. (1.8)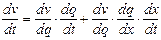 . (1.9)
. (1.9) . (1.10)
. (1.10) . (1.11)
. (1.11) , (1.12)
, (1.12) можно интерпретировать, как коэффициент трения в случае динамики жидкостей. Для классической сжимаемой жидкости уравнение (1.12) носит название уравнения движения и имеет вид:
можно интерпретировать, как коэффициент трения в случае динамики жидкостей. Для классической сжимаемой жидкости уравнение (1.12) носит название уравнения движения и имеет вид: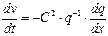 , (1.13)
, (1.13)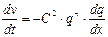 . (1.14)
. (1.14)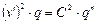 . (1.15)
. (1.15)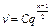 , выполним разделение переменных и проинтегрируем
, выполним разделение переменных и проинтегрируем . (1.16)
. (1.16)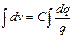 . (1.17)
. (1.17)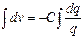
 начальные условия q=qmax, при v=0
начальные условия q=qmax, при v=0

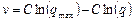

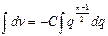 ;
;  начальные условия q=qmax, при v=0
начальные условия q=qmax, при v=0
 ;
; 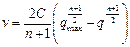
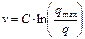 , (1.18)
, (1.18) , (1.19)
, (1.19)

 (1.20)
(1.20)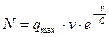 . (1.21)
. (1.21) . (1.22)
. (1.22) (1.23)
(1.23)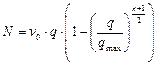 (1.24)
(1.24)

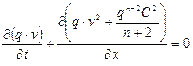 . (1.25)
. (1.25)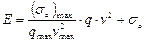 . (1.32)
. (1.32)
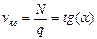 (1.33)
(1.33) (1.34)
(1.34) . (1.35)
. (1.35)

 (1.36)
(1.36) (1.37)
(1.37) . (1.38)
. (1.38)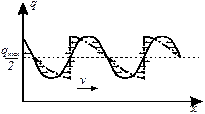
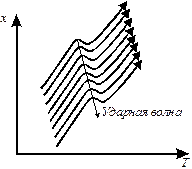
 . 1.39)
. 1.39)
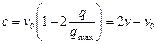 . (1.40)
. (1.40) (1.41)
(1.41)
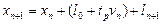 , (1.42)
, (1.42) , (1.43)
, (1.43) (1.44)
(1.44) , (1.45)
, (1.45) . (1.46)
. (1.46)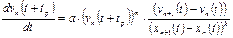 , (1.47)
, (1.47)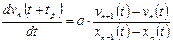 . (1.48)
. (1.48) . (1.49)
. (1.49) . (1.50)
. (1.50)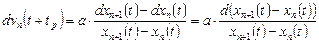 . (1.51)
. (1.51) , (1.52)
, (1.52) . (1.53)
. (1.53) . (1.54)
. (1.54)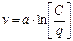 . (1.55)
. (1.55)
 (1.56)
(1.56)


