Пусть распределение возбуждения в линейном излучателе имеет вид
 , (10.8)
, (10.8)
ряда из некоторых известных функций 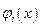 . Подставим этот ряд в выражение для характеристики направленности антенны (10.6)
. Подставим этот ряд в выражение для характеристики направленности антенны (10.6)
 (10.9)
(10.9)
Здесь зависящая от текущего номера (i) функция
 ,
, 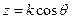
представляет собой парциальную диаграмму направленности, соответствующую функции распределения возбуждения 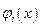 . Теперь заданная функция диаграммы направленности
. Теперь заданная функция диаграммы направленности 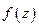 может быть аппроксимирована с помощью ряда (10.9). Для этого потребуется вычислить необходимые коэффициенты (
может быть аппроксимирована с помощью ряда (10.9). Для этого потребуется вычислить необходимые коэффициенты ( ) и затем найти функцию распределения возбуждения излучателя с помощью формулы (10.8). Все эти действия и представляют сущность метода синтеза ДН с помощью парциальных диаграмм направленности.
) и затем найти функцию распределения возбуждения излучателя с помощью формулы (10.8). Все эти действия и представляют сущность метода синтеза ДН с помощью парциальных диаграмм направленности.
Наиболее просто этот метод реализуется при среднеквадратичном приближении, а в качестве системы функций  берутся любые полные функции, удовлетворяющие условию ортогональности на интервале
берутся любые полные функции, удовлетворяющие условию ортогональности на интервале 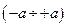 .
.



 .
.
В этом случае коэффициенты аппроксимации [  ] могут быть вычислены по заданной ДН
] могут быть вычислены по заданной ДН 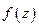 как коэффициенты Фурье разложения:
как коэффициенты Фурье разложения:
 (10.10)
(10.10)
Функция  является преобразованием Фурье от функции распределения
является преобразованием Фурье от функции распределения 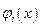 , отличным от нуля на интервале
, отличным от нуля на интервале  . Поэтому функции
. Поэтому функции  будут представлять собой целые функции степени, не превышающей
будут представлять собой целые функции степени, не превышающей  .
.
В качестве парциальных ДН и в качестве соответствующих гармоник возбуждения в антенной технике, широко используется следующая система парциальных диаграмм:
 (10.11)
(10.11)
Эти функции образуют ортогональную систему диаграмм и ортогональную систему распределения возбуждения на интервале  .
.
Выразим заданную функцию диаграммы направленности 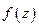 в виде ряда:
в виде ряда:
 (10.12)
(10.12)
Фактически ряд (10.12) представляет собой интерполяционный ряд Котельникова для целых функций степени, не превышающей ( ) на всей оси (z).
) на всей оси (z).
Особенностью системы парциальных диаграмм (10.11) является то, что в точках  , только одна диаграмма с номером
, только одна диаграмма с номером  имеет максимум, а все остальные парциальные диаграммы в этой точке равны нулю. В силу этого, неизвестные коэффициенты разложения (
имеет максимум, а все остальные парциальные диаграммы в этой точке равны нулю. В силу этого, неизвестные коэффициенты разложения ( ), входящие в формулу (10.12), будут являться равноотстоящими выборками заданной функции направленности
), входящие в формулу (10.12), будут являться равноотстоящими выборками заданной функции направленности 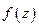 :
:
 ,
,  (10.13)
(10.13)
Для определения всех коэффициентов ( ) функция
) функция 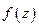 должна быть известна на всей оси (z). Тут возможно два подхода определения функции:
должна быть известна на всей оси (z). Тут возможно два подхода определения функции:
· функцию 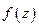 аналитически продолжена на всю ось z, как целая функция степени не выше
аналитически продолжена на всю ось z, как целая функция степени не выше  , что ведет к точному воспроизведению направленности, но решение может оказаться некорректным;
, что ведет к точному воспроизведению направленности, но решение может оказаться некорректным;
· заданная функция 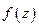 приравнивается к нулю вне интервале
приравнивается к нулю вне интервале  .
.
Но, это дает возможность найти только первые  коэффициенты ряда Котельникова и синтезируемая диаграмма направленности будет определяться так:
коэффициенты ряда Котельникова и синтезируемая диаграмма направленности будет определяться так:
 , (10.14)
, (10.14)
где  , а N равна целому числу отношения (L/λ), f(idz) = ai.
, а N равна целому числу отношения (L/λ), f(idz) = ai.
Необходимое распределение возбуждения, для получения синтезируемой ДН, определяется конечным рядом Фурье:
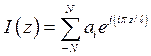 (10.15)
(10.15)
Решение задачи в виде уравнений (10.14), (10.15) будет удовлетворять условию корректности, однако полученная ДН будет совпадать с заданной функцией 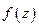 только в точках отсчета.
только в точках отсчета.



 , (10.8)
, (10.8)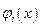 . Подставим этот ряд в выражение для характеристики направленности антенны (10.6)
. Подставим этот ряд в выражение для характеристики направленности антенны (10.6) (10.9)
(10.9) ,
, 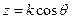
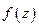 может быть аппроксимирована с помощью ряда (10.9). Для этого потребуется вычислить необходимые коэффициенты (
может быть аппроксимирована с помощью ряда (10.9). Для этого потребуется вычислить необходимые коэффициенты ( ) и затем найти функцию распределения возбуждения излучателя с помощью формулы (10.8). Все эти действия и представляют сущность метода синтеза ДН с помощью парциальных диаграмм направленности.
) и затем найти функцию распределения возбуждения излучателя с помощью формулы (10.8). Все эти действия и представляют сущность метода синтеза ДН с помощью парциальных диаграмм направленности. берутся любые полные функции, удовлетворяющие условию ортогональности на интервале
берутся любые полные функции, удовлетворяющие условию ортогональности на интервале 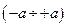 .
.


 .
. (10.10)
(10.10) . Поэтому функции
. Поэтому функции  .
. (10.11)
(10.11) .
. (10.12)
(10.12) ) на всей оси (z).
) на всей оси (z). , только одна диаграмма с номером
, только одна диаграмма с номером  имеет максимум, а все остальные парциальные диаграммы в этой точке равны нулю. В силу этого, неизвестные коэффициенты разложения (
имеет максимум, а все остальные парциальные диаграммы в этой точке равны нулю. В силу этого, неизвестные коэффициенты разложения ( ,
,  (10.13)
(10.13) ) функция
) функция  коэффициенты ряда Котельникова и синтезируемая диаграмма направленности будет определяться так:
коэффициенты ряда Котельникова и синтезируемая диаграмма направленности будет определяться так: , (10.14)
, (10.14) , а N равна целому числу отношения (L/λ), f(idz) = ai.
, а N равна целому числу отношения (L/λ), f(idz) = ai.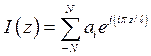 (10.15)
(10.15)


