

Механическое удерживание земляных масс: Механическое удерживание земляных масс на склоне обеспечивают контрфорсными сооружениями различных конструкций...

Индивидуальные и групповые автопоилки: для животных. Схемы и конструкции...

Механическое удерживание земляных масс: Механическое удерживание земляных масс на склоне обеспечивают контрфорсными сооружениями различных конструкций...

Индивидуальные и групповые автопоилки: для животных. Схемы и конструкции...
Топ:
Характеристика АТП и сварочно-жестяницкого участка: Транспорт в настоящее время является одной из важнейших отраслей народного...
Когда производится ограждение поезда, остановившегося на перегоне: Во всех случаях немедленно должно быть ограждено место препятствия для движения поездов на смежном пути двухпутного...
Генеалогическое древо Султанов Османской империи: Османские правители, вначале, будучи еще бейлербеями Анатолии, женились на дочерях византийских императоров...
Интересное:
Наиболее распространенные виды рака: Раковая опухоль — это самостоятельное новообразование, которое может возникнуть и от повышенного давления...
Национальное богатство страны и его составляющие: для оценки элементов национального богатства используются...
Мероприятия для защиты от морозного пучения грунтов: Инженерная защита от морозного (криогенного) пучения грунтов необходима для легких малоэтажных зданий и других сооружений...
Дисциплины:
|
из
5.00
|
Заказать работу |
|
|
|
|
Свойства сходящихся рядов.
· Если сходится ряд:  , то сходится и ряд:
, то сходится и ряд:  , и обратно. Другими словами на сходимость ряда не влияет отбрасывание любого конечного числа его первых членов.
, и обратно. Другими словами на сходимость ряда не влияет отбрасывание любого конечного числа его первых членов.
Сходящиеся ряды можно умножать на число, почленно складывать и вычитать так же, как и конечные суммы:
· Если сходится ряд:  и его сумма равна S, то и ряд
и его сумма равна S, то и ряд  где С = const, сходится и его сумма равна СS.
где С = const, сходится и его сумма равна СS.
· Если сходятся ряды:  и
и  и их суммы равны Sа и Sb, то и ряд
и их суммы равны Sа и Sb, то и ряд  , сходится и его сумма равна Sа ± Sb.
, сходится и его сумма равна Sа ± Sb.
Необходимое условие сходимости ряда:
Если ряд  сходится, то его общий член стремится к нулю, то есть
сходится, то его общий член стремится к нулю, то есть 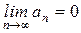 . Данное условие не является достаточным.
. Данное условие не является достаточным.
Рассмотрим гармонический ряд:  и он расходится.
и он расходится.
Задание 2. Написать первые пять членов ряда и исследовать ряд на сходимость:
 Необходимое условие сходимости ряда выполняется:
Необходимое условие сходимости ряда выполняется:  .
Данный ряд является геометрической прогрессией, в которой .
Данный ряд является геометрической прогрессией, в которой
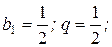 Так как
Так как  , то ряд сходится. , то ряд сходится.
| 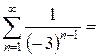 Необходимое условие сходимости ряда
_________________:
Необходимое условие сходимости ряда
_________________:  Данный ряд является геометрической прогрессией, в которой
Данный ряд является геометрической прогрессией, в которой
 Так как
Так как  , то ряд ________________. , то ряд ________________.
|
 Необходимое условие сходимости ряда выполняется:
Необходимое условие сходимости ряда выполняется:  .
Данный ряд является геометрической прогрессией, в которой .
Данный ряд является геометрической прогрессией, в которой
 Так как
Так как  , то ряд сходится. , то ряд сходится.
|  Необходимое условие сходимости ряда
_________________:
Необходимое условие сходимости ряда
_________________:  Данный ряд является геометрической прогрессией, в которой
Данный ряд является геометрической прогрессией, в которой
 Так как
Так как  , то ряд _______________. , то ряд _______________.
|

| 
|
Знакопеременный ряд. Признак Лейбница
Ряд называется знакопеременным, если его члены поочерёдно положительны и отрицательны:  , где аn>0.
, где аn>0.
Признак Лейбница: Знакопеременный ряд сходится, если его члены стремятся к нулю всё время убывая по абсолютному значению. Итак, должны выполняться два условия:
1)  ;
;
2)  .
.
Замечание: остаток такого ряда имеет тот же знак, что и первый отбрасываемый член, и меньше его по абсолютному значению.
Задание 6. Исследовать ряд на сходимость по признаку Лейбница:
 Применим признак Лейбница для знакопеременного ряда.
Так как члены ряда стремятся к нулю всё время убывая по абсолютному значению, следовательно, ряд сходится:
Применим признак Лейбница для знакопеременного ряда.
Так как члены ряда стремятся к нулю всё время убывая по абсолютному значению, следовательно, ряд сходится:
 Ответ: ряд сходится.
Ответ: ряд сходится.
|  Ответ: ряд _________________.
Ответ: ряд _________________.
|

| 
|
Степенной ряд.
Степенным рядом называется ряд вида (1): ао+а1х+а2х2+...+апхп+...,
а также ряд более общего вида (2): ао+а1 (х-х0) +а2х2 (х-х0) 2+...+апхп (х-х0) n+...,
говорят, что он расположен соответственно по степеням х, о или по степеням х - х0.
Постоянные а0, a1,..., ап,... называются коэффициентами степенного ряда.
Если обозначить х-х0 через z, то ряд (2) окажется расположенным по степеням z, т. е. примет вид (1). Поэтому в дальнейшем, если особо не оговорено, степенным рядом именуется ряд вида (1). Степенной ряд всегда сходится при х =0.
Относительно сходимости его в других точках могут представиться три случая
1) степенной ряд может расходится во всех точках, кроме х =0, например,
11х1+22х2+33х3+…+ ппхп+...,
2) степенной ряд может сходиться во всех точках, например,

3) степенной ряд может сходиться в одних точках и расходится в других.
Ответ: (-3; -1).
Тест 5. Ряды.
| Вопрос 1Укажите гармонический ряд | |||
а.) 
| б.) 
| в.) 
| г.) |
| Вопрос 2Укажите ряд, относящийся к обобщённому гармоническому ряду | |||
а.) 
| б.) 
| в.) 
| г.) |
| Вопрос 3Укажите ряд, относящийся к геометрической прогрессии | |||
а.) 
| б.) 
| в.) 
| г.) |
| Вопрос 4Выберите сходящиеся ряды | |||
а.) 
| б.) 
| в.) 
| г.) |
| Вопрос 5Выберите сходящиеся ряды | |||
а.) 
| б.) 
| в.) 
| г.) |
| Вопрос 6Выберите расходящиеся ряды | |||
а.) 
| б.) 
| в.) 
| г.) |
| Вопрос 7Выберите расходящиеся ряды | |||
а.) 
| б.) 
| в.) 
| г.) |
Вопрос 8Найдите радиус сходимости степенного ряда 
| |||
а.) 
| б.) 7 | в.) 
| г.) |
Вопрос 9Найдите радиус сходимости степенного ряда 
| |||
а.) 
| б.) 6 | в.) 
| г.) |
Вопрос 10Найдите интервал сходимости степенного ряда 
| |||
| а.) (0; 3) | б.) (-3; 3) | в.) 
| г.) |
Вопрос 11Найдите интервал сходимости степенного ряда 
| |||
| а.) (-5; 5) | б.) (-3; 7) | в.) (-7; 3) | г.) |
Вопрос 12Найдите интервал сходимости степенного ряда 
| |||
| а.) (-1; 7) | б.) (-4; 4) | в.) (-7; 1) | г.) |
| Вопрос 13Укажите знакопеременный ряд | |||
а.) 
| б.) 
| в.) 
| г.) |
| Вопрос 14Укажите положительный ряд | |||
а.) 
| б.) 
| в.) 
| г.) |
Свойства сходящихся рядов.
· Если сходится ряд:  , то сходится и ряд:
, то сходится и ряд:  , и обратно. Другими словами на сходимость ряда не влияет отбрасывание любого конечного числа его первых членов.
, и обратно. Другими словами на сходимость ряда не влияет отбрасывание любого конечного числа его первых членов.
Сходящиеся ряды можно умножать на число, почленно складывать и вычитать так же, как и конечные суммы:
· Если сходится ряд:  и его сумма равна S, то и ряд
и его сумма равна S, то и ряд  где С = const, сходится и его сумма равна СS.
где С = const, сходится и его сумма равна СS.
· Если сходятся ряды:  и
и  и их суммы равны Sа и Sb, то и ряд
и их суммы равны Sа и Sb, то и ряд  , сходится и его сумма равна Sа ± Sb.
, сходится и его сумма равна Sа ± Sb.
Необходимое условие сходимости ряда:
Если ряд  сходится, то его общий член стремится к нулю, то есть
сходится, то его общий член стремится к нулю, то есть 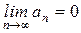 . Данное условие не является достаточным.
. Данное условие не является достаточным.
Рассмотрим гармонический ряд:  и он расходится.
и он расходится.
Задание 2. Написать первые пять членов ряда и исследовать ряд на сходимость:
 Необходимое условие сходимости ряда выполняется:
Необходимое условие сходимости ряда выполняется:  .
Данный ряд является геометрической прогрессией, в которой .
Данный ряд является геометрической прогрессией, в которой
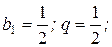 Так как
Так как  , то ряд сходится. , то ряд сходится.
| 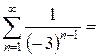 Необходимое условие сходимости ряда
_________________:
Необходимое условие сходимости ряда
_________________:  Данный ряд является геометрической прогрессией, в которой
Данный ряд является геометрической прогрессией, в которой
 Так как
Так как  , то ряд ________________. , то ряд ________________.
|
 Необходимое условие сходимости ряда выполняется:
Необходимое условие сходимости ряда выполняется:  .
Данный ряд является геометрической прогрессией, в которой .
Данный ряд является геометрической прогрессией, в которой
 Так как
Так как  , то ряд сходится. , то ряд сходится.
|  Необходимое условие сходимости ряда
_________________:
Необходимое условие сходимости ряда
_________________:  Данный ряд является геометрической прогрессией, в которой
Данный ряд является геометрической прогрессией, в которой
 Так как
Так как  , то ряд _______________. , то ряд _______________.
|

| 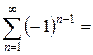
|
Достаточные признаки сходимости положительных рядов
Необходимое и достаточное условие сходимости положительного ряда: Для того чтобы ряд  с неотрицательными членами сходился необходимо и достаточно, чтобы последовательность частичных сумм этого ряда была ограничена.
с неотрицательными членами сходился необходимо и достаточно, чтобы последовательность частичных сумм этого ряда была ограничена.
Признаки сравнения:
· (сходимости) - Пусть даны два ряда с неотрицательными членами  и
и  и для всех n выполняется неравенство
и для всех n выполняется неравенство  . Тогда если ряд
. Тогда если ряд  сходится, то ряд
сходится, то ряд  тоже сходится;
тоже сходится;
· (расходимости) - Пусть даны два ряда с неотрицательными членами  и
и  и для всех n выполняется неравенство
и для всех n выполняется неравенство 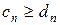 . Тогда если ряд
. Тогда если ряд  расходится, то ряд
расходится, то ряд  тоже расходится.
тоже расходится.
Признак Даламбера: Пусть дан ряд с положительными членами  и существует
и существует  .
.
· если q<1 – ряд сходится;
· если q>1 – ряд расходится;
· если q=1 – ряд может и сходиться и расходиться, то есть данный признак неприменим.
Признак Коши: Пусть дан ряд с положительными членами  и существует
и существует  .
.
· если q<1 – ряд сходится;
· если q>1 – ряд расходится;
· если q=1 – ряд может и сходиться и расходиться, то есть данный признак неприменим.
Интегральный признак: Пусть дан ряд  с положительными членами, являющимися значениями некоторой функции f (x), непрерывной и убывающей на полуинтервале [1; +¥). Тогда ряд
с положительными членами, являющимися значениями некоторой функции f (x), непрерывной и убывающей на полуинтервале [1; +¥). Тогда ряд  будет сходиться в том случае, если сходится несобственный интеграл:
будет сходиться в том случае, если сходится несобственный интеграл: 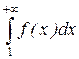 и расходиться в случае его расходимости.
и расходиться в случае его расходимости.
Обобщённый гармонический ряд:  :
:
· сходится при a>1;
· расходится при 0<a£1.
| Ряд | Геометрическая прогрессия | Обобщённый гармонический ряд |

| 
| |
| Сходится | |q|<1 | a>1 |
| Расходится | |q|³1 | 0<a£1 |
Задание 3. Исследовать ряд на сходимость, используя признаки сравнения:

| 
|

| 
|

| 
|

| 
|
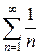
| 
|

| 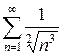
|

| 
|
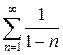
| 
|

| 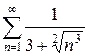
|

| 
|

| 
|
Задание 4. Исследовать ряд на сходимость по признаку Даламбера:
 Применим признак Даламбера для данного положительного ряда:
Применим признак Даламбера для данного положительного ряда:
 Имеем:
Имеем:
 Итак, ряд _____________________________.
Итак, ряд _____________________________.
| 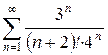 Итак, ряд _____________________________.
Итак, ряд _____________________________.
|

| 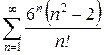
|
Задание 5. Исследовать ряд на сходимость по признаку Коши:
 Применим признак Коши:
Применим признак Коши:
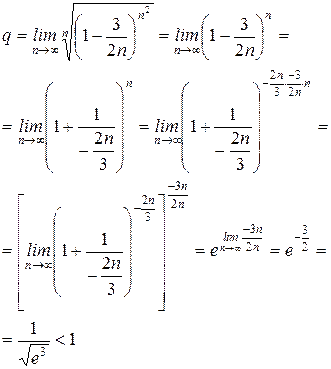 Итак, ряд______________________________.
Итак, ряд______________________________.
|  Применим признак Коши:
Итак, ряд____________________________.
Применим признак Коши:
Итак, ряд____________________________.
|

| 
|
|
|
|

Состав сооружений: решетки и песколовки: Решетки – это первое устройство в схеме очистных сооружений. Они представляют...

История развития хранилищ для нефти: Первые склады нефти появились в XVII веке. Они представляли собой землянные ямы-амбара глубиной 4…5 м...

Археология об основании Рима: Новые раскопки проясняют и такой острый дискуссионный вопрос, как дата самого возникновения Рима...

Своеобразие русской архитектуры: Основной материал – дерево – быстрота постройки, но недолговечность и необходимость деления...
© cyberpedia.su 2017-2025 - Не является автором материалов. Исключительное право сохранено за автором текста.
Если вы не хотите, чтобы данный материал был у нас на сайте, перейдите по ссылке: Нарушение авторских прав. Мы поможем в написании вашей работы!