Estimated Autocorrelations for Y1

 

			Lower 95,0%	Upper 95,0%
Lag	Autocorrelation	Stnd. Error	Prob. Limit	Prob. Limit
	0,449877	0,119523	-0,234261	0,234261
	0,535451	0,141662	-0,277654	0,277654
	0,220373	0,168107	-0,329484	0,329484
	0,207219	0,172184	-0,337476	0,337476
	0,194737	0,175711	-0,344388	0,344388
	0,310867	0,178767	-0,350378	0,350378
	0,233097	0,18633	-0,365201	0,365201
	0,40425	0,19045	-0,373276	0,373276
	0,201049	0,202337	-0,396575	0,396575
	0,201652	0,205171	-0,402129	0,402129
	0,0235754	0,207983	-0,407641	0,407641
	0,0532864	0,208022	-0,407716	0,407716
	-0,0220809	0,208216	-0,408098	0,408098
	0,0198663	0,20825	-0,408163	0,408163
	-0,0106041	0,208277	-0,408216	0,408216
	0,00121957	0,208285	-0,408231	0,408231
	-0,0234093	0,208285	-0,408232	0,408232
	0,00678961	0,208322	-0,408305	0,408305
	-0,0436647	0,208326	-0,408311	0,408311
	-0,024831	0,208456	-0,408568	0,408568
	-0,0443627	0,208499	-0,40865	0,40865
	-0,060177	0,208633	-0,408915	0,408915
	-0,0694362	0,208881	-0,4094	0,4094

 

Автокорреляции есть т.к. значения выходят за пределы доверительного интервала.

Ряд Y1 является нестационарным т.к. дисперсии не равны

Y2: цена закрытия:

1. График динамики временного ряда

Рисунок 7:HorizontalTimeSeriesPlot – график динамики временного ряда

Проверка на стационарность рада Y2:

Проверка гипотезы о равенстве дисперсий

Comparison of Means for Y2

95,0% confidence interval for mean of Col_5<=35=0: 41,9021 +/- 1,31224 [40,5899; 43,2144]

95,0% confidence interval for mean of Col_5<=35=1: 31,0509 +/- 3,54555 [27,5053; 34,5964]

95,0% confidence interval for the difference between the means

assuming equal variances: 10,8513 +/- 3,71218 [7,13907; 14,5634]

 

t test to compare means

Null hypothesis: mean1 = mean2

Alt. hypothesis: mean1 NE mean2

assuming equal variances: t = 5,83306 P-value = 1,66052E-7

Reject the null hypothesis for alpha = 0,05.

Принимаем гипотезу H1: дисперсии не равны

Это признак нестационарности процесса.

Проверка гипотезы о равенстве средних (при неравных дисперсиях)

Comparison of Standard Deviations for Y2

	Col_5<=35=0	Col_5<=35=1
Standard deviation	3,82006	10,3215
Variance	14,5929	106,533
Df

Ratio of Variances = 0,13698

 

95,0% Confidence Intervals

Standard deviation of Col_5<=35=0: [3,08994; 5,00505]

Standard deviation of Col_5<=35=1: [8,34874; 13,5232]

Ratio of Variances: [0,069143; 0,271375]

 

F-test to Compare Standard Deviations

Null hypothesis: sigma1 = sigma2

Alt. hypothesis: sigma1 NE sigma2

F = 0,13698 P-value = 8,06996E-8

Reject the null hypothesis for alpha = 0,05.

Принимаем гипотезу H1: средние не равны

Это признак нестационарности процесса.

Проверка на автокорреляцию

2. График автокорреляционной функции (АКФ)

Рисунок 8: AutocorrelationFunction – график автокорреляционной функции

3 График частной автокорреляционной функции (ЧАКФ)

Рисунок 9: Partial Autocorrelation Function – график частной автокорреляционной функции

 

 

Estimated Autocorrelations for Y2

 

			Lower 95,0%	Upper 95,0%
Lag	Autocorrelation	Stnd. Error	Prob. Limit	Prob. Limit
	0,933555	0,119523	-0,234261	0,234261
	0,856271	0,197956	-0,387987	0,387987
	0,778122	0,245224	-0,480632	0,480632
	0,696092	0,27827	-0,5454	0,5454
	0,614816	0,302123	-0,592151	0,592151
	0,545849	0,319497	-0,626204	0,626204
	0,486009	0,332553	-0,651792	0,651792
	0,422506	0,342549	-0,671385	0,671385
	0,352582	0,349915	-0,685821	0,685821
	0,280722	0,354954	-0,695698	0,695698
	0,211646	0,358111	-0,701886	0,701886
	0,144822	0,359894	-0,70538	0,70538
	0,08675	0,360725	-0,70701	0,70701
	0,0761256	0,361023	-0,707594	0,707594
	0,0641558	0,361252	-0,708043	0,708043
	0,0495364	0,361415	-0,708362	0,708362
	0,0311312	0,361512	-0,708552	0,708552
	0,0154962	0,36155	-0,708627	0,708627
	0,00109189	0,36156	-0,708646	0,708646
	-0,0124333	0,36156	-0,708646	0,708646
	-0,0287448	0,361566	-0,708658	0,708658
	-0,0465625	0,361599	-0,708722	0,708722
	-0,0615572	0,361684	-0,70889	0,70889

 

Автокорреляция 5 порядка т.к. 5 значения выходят за пределы доверительного интервала.

Ряд Y2 не является стационарным т.к. дисперсии не равны и присутствует автокорреляция 5 порядка.

 

Y3: Средневзвешенная цена

1. График динамики временного ряда

Рисунок 10:HorizontalTimeSeriesPlot – график динамики временного ряда

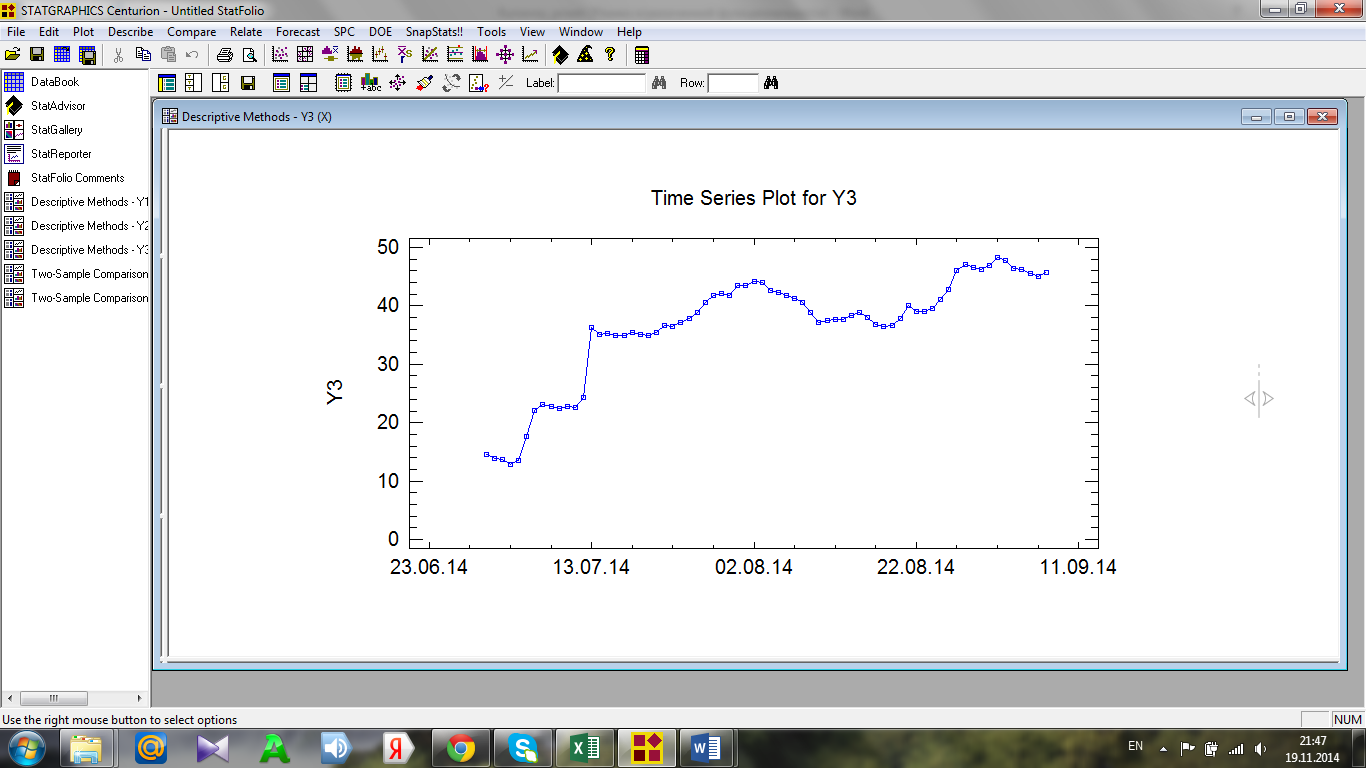
Проверка на стационарность рада Y3:

Проверка гипотезы о равенстве дисперсий

Comparison of Means for Y3

95,0% confidence interval for mean of Col_5<=35=0: 41,6927 +/- 1,33806 [40,3546; 43,0307]

95,0% confidence interval for mean of Col_5<=35=1: 31,1935 +/- 3,53333 [27,6602; 34,7269]

95,0% confidence interval for the difference between the means

assuming equal variances: 10,4991 +/- 3,70983 [6,78931; 14,209]

 

t test to compare means

Null hypothesis: mean1 = mean2

Alt. hypothesis: mean1 NE mean2

assuming equal variances: t = 5,64736 P-value = 3,47377E-7

Reject the null hypothesis for alpha = 0,05.

Принимаем гипотезу H1: дисперсии не равны

Это признак нестационарности процесса.

Проверка гипотезы о равенстве средних (при неравных дисперсиях)