Существует несколько номенклатур для обозначения симметрии кристаллов. Мы рассмотрим три из них:
- кристаллографическая (по Бравэ);
- международная (интернациональная);
- по Шенфлису.
Обозначение видов симметрии по номенклатуре Бравэ составляется следующим образом: записывается весь набор элементов симметрии, который реализуется в данном кристалле (см. табл.1), сначала записываются оси симметрии начиная с наибольшего порядка, затем плоскости симметрии в конце отмечается наличие центра симметрии. Если одинаковых элементов
симметрии несколько, то их количество ставится перед обозначением этого элемента арабской цифрой.
Например: 3L44L36L29PC – в кристалле есть 3 поворотные оси симметрии 4-го порядка, 4 поворотные оси симметрии 3-го порядка, 6 осей 2-го порядка, 9 плоскостей симметрии и центр; аксиально-центральный вид симметрии, кубическая сингония, высшая категория.
Обозначение кристаллов по международной (интернациональной) символике, в этой номенклатуре записываются только основные «порождающие» элементы симметрии, а остальные «порожденные», которые можно с помощью теорем о сложении и сочетании элементов симметрии можно вывести из «порождающих» не записываются. В качестве «порождающих» предпочтение отдается плоскостям. Правила записи международного символа представлены в табл.
Таблица 4
Причем используют следующие символы помимо представленных ранее (см.табл.1): 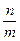 , n/m - ось симметрии n-го порядка и перпендикулярная ей плоскость симметрии.
, n/m - ось симметрии n-го порядка и перпендикулярная ей плоскость симметрии.
Например: 4/mmm – можно прочитать так: ось 4-го порядка (вдоль Z) и перпендикулярная ей плоскость («порождающие»), дают центр симметрии (теорема 2); mm – плоскость симметрии (в направлении X,Y и по диагонали) вдоль оси 4 («порождающие») – по теореме 4, таких плоскостей четыре, таким образом имеем горизонтальные и вертикальные плоскости (перпендикулярные друг другу), а значит линиями их пересечений (теорема 1) будут оси 2, расположенные перпендикулярно оси 4, значит таких осей 2-го порядка будет 4 (теорема 3), по номенклатуре Бравэ данный вид симметрии записывается так: L44L24PC.
Обозначение кристаллов по номенклатуре Шенфлиса строится следующим образом табл. Таблица 5,Таблица 6.
Таблица 4 – Правила записи международного символа
| Сингония
| Позиция в символе
|
| 1-я
| 2-я
| 3-я
|
| Триклинная
| Только один символ, соответствующий любому направлению в кристалле
|
| Моноклинная
| Единственная ось 2 или плоскость m в соответствии с правилами установки
|
| Ромбическая
| Ось 2 или плоскость m вдоль оси X
| Ось 2 или плоскость m вдоль оси Y
| Ось 2 или плоскость m вдоль оси Z
|
| Тригональная
| Главная ось симметрии
| Оси 2 или плоскость m вдоль X, Y, Y'
| Диагональные оси 2 или плоскости m
|
| Гексагональная
|
| Тетрагональная
| Оси 2 или плоскость m вдоль X, Y
|
| Кубическая
| Координатные* оси симметрии
| Оси 3
| Диагональные* элементы симметрии
|
Таблица 5 - Обозначение классов (видов) симметрии средней и низшей категорий по Шенфлису

Таблица 6 – Обозначение классов (видов) симметрии кристаллов высшей категории по Шенфлису

Вида симметрии
Все 32 вида симметрии с обозначениями по трем известным номенклатурам представлены в табл.Таблица 7,Таблица 8 иТаблица 9.
Можно заметить, что некоторые кристаллы могут быть отнесены одновременно к двум видам (классам) симметрии. Например, инверсионно-примитивный и центральный для триклинной и тригональной сингоний.
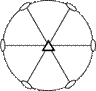
Вид симметрии инверсионно-примитивный гексагональной сингонии может быть отнесен к тригональной сингонии. При изображении стереографической проекции инверсионно-планального вида симметрии гексагональной сингонии принято не отмечать существование горизонтальной плоскости симметрии (см. табл.Таблица 8). Существуют сочетания элементов симметрии, которые однозначно (тождественно) заменяются третьим:
- 3 + С º 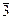 (ось 3-го порядка и центр симметрии дают ось инверсии 3 го порядка);
(ось 3-го порядка и центр симметрии дают ось инверсии 3 го порядка);
- 3 + ^m º 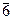 (ось 3-го порядка и перпендикулярная плоскость дают ось инверсии 6 го порядка).
(ось 3-го порядка и перпендикулярная плоскость дают ось инверсии 6 го порядка).
Таблица 7 – Виды симметрии кристаллов низшей категории
| Сингония
| Вид симметрии
|
| Примитивный
| Инверсионно-примитивный
| Центральный
| Аксиальный
| Планальный
| Инверсионно-планальный
| Аксиально-центральный
|
| Триклинная
| 
| L1
1
C1
| 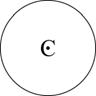
| Li1
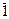 C
C 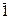
|
|
|
|
|
| Моноклинная
|
|
|
| 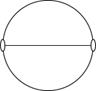
| L2
2
C2
| 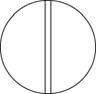
| P
m
C1h, (Cs)
|
| 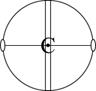
| L2PC
2/m
C2h
|
| Ромбическая
|
|
|
| 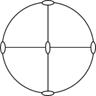
| 3L2
22, (222)
D2
| 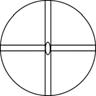
| L22P
2m, (mm2, 2mm)
C2v
|
| 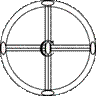
| 3L23PC
2/mm, (mmm)
D2h
|
| | | | | | | | | | | | | | | |
Таблица 8 – Виды симметрии кристаллов средней категории
| Cингония
| Вид симметрии
|
| Примитивный
| Инверсионно-примитивный
| Центральный
| Аксиальный
| Планальный
| Инверсионно-планальный
| Аксиально-центральный
|
| Тригональная
| 
| L3
3
C3
| 
| Li3
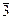
C 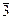 , S3 , S3
| 
| Li3
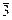 C
C 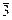 , S3 , S3
| 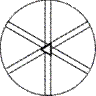
| L33L2
32
D3
| 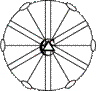
| Li33L23P
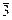 m
D3d m
D3d
|
| Тетрагональная
| 
L4
4
C4
| 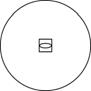
Li4
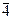
C 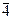 , S4 , S4
|  L4PC
4/m
C4h
L4PC
4/m
C4h
| 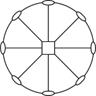
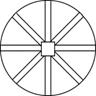
L44L2
42
D4
| 
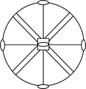
L44P
4m
C4v
|  Li42L22P
Li42L22P
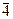 m
D2d m
D2d
| 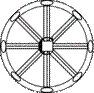
L44L24PC
4/mm (4/mmm)
D4h
|
| Гексагональная
| 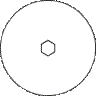
L6
6
C6
| 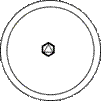
L3P
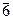
C3h
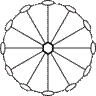
| 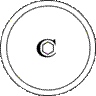 L6PC
6/m
C6h
L6PC
6/m
C6h
| 
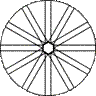
L66L2
62, (622)
D6
| 
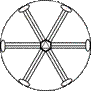
L66P
6m, (6mm)
C6v
|  Li63L23P
Li63L23P
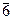 2m, ( 2m, (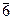 m2)
D3h m2)
D3h
| 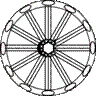
L66L26PC
6/mm, (6/mmm)
D6h
|
| | | | | | | | | | | | | |
Таблица 9 – Виды симметрии кристаллов высшей категории (кубическая сингония)
| Вид симметрии
| Стереографическая проекция
| Обозначения
|
| Примитивный
| 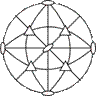
| 4L33L2
23
T
|
| Инверсионно-примитивный
|
|
|
| Центральный
| 
| 4L3 3L23P
m3
Th
|
| Аксиальный
| 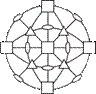
| 3L44L36L2
432
O
|
| Планальный
|
|
|
| Инверсионно-планальный
| 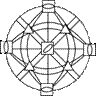
| 3Li44L36P
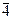 3m
Td 3m
Td
|
| Аксиально-центральный
| 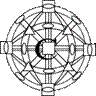
| 3L44L36L29PC
m3m
Oh
|
Простые формы
Простой (идеальной) формой кристалла называется многогранник, все грани которого модно получить из одной грани с помощью преобразований симметрии, свойственных классу симметрии (точечной группе) данного кристалла. Все грани одной простой формы одинаковы по форме и площади, скорости роста граней одной простой формы равны.
Существуют частные и общие простые формы:
- Частная простая форма получается, если исходная грань располагается параллельно или перпендикулярно осям или плоскостям симметрии кристалла или если она образует одинаковые углы с двумя равными элементами симметрии. Частных простых форм в кристалле может быть несколько
- Общая простая форма получается, если исходная грань задана в общем положении, т.е. не на элементах симметрии. Общая простая форма в кристалле может быть одна.
Всего существует 47 простых форм. Сначала рассмотрим простые формы кристаллов низшей и средней категорий:
- Моноэдр (от греч. "моно"- один, "эдра"- грань) – простая форма, представленная одной единственной гранью (рис.Рисунок 6 (1)). Моноэдром является, например, основание пирамиды.
- Пинакоид (от греч."пинакс"- доска) – простая форма, состоящая из двух равных параллельных граней, часто обратно ориентированных (рис.Рисунок 6 (2)).
- Диэдр (от греч."ди" - два, "эдр"- грань) – простая форма, образованная двумя равными пересекающимися (иногда на своем продолжении) гранями, образующими "прямую крышу" (рис.Рисунок 6 (3)). Существует осевой (грани пересекаются по оси 2-го порядка) и плоскостной диэдр (грани связаные между собой плоскостью симметрии).
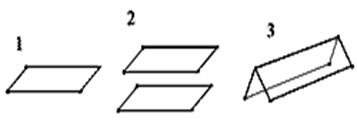
Рисунок 6 – простые формы 1 – моноэдр; 2 – пинакоид; 3 – диэдр
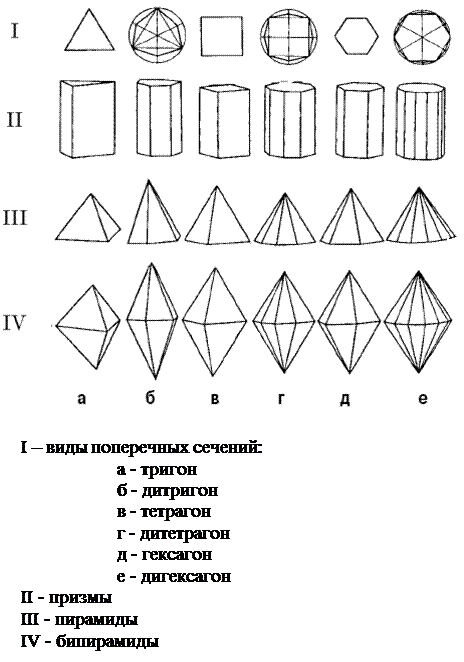
- Призма – простая форма, которая состоит из равных граней параллельных какой либо из осей координат (Приложение 1, ряд II). В низшей категории призмы могут быть только ромбическими (в сечении - ромб). Грани призмы кристаллов средней категории параллельны главной оси высшего порядка, а в зависимости от формы сечения, которое при этом получается могут называться:
- тригональной – если в сечении треугольник (тригон);
- дитригональной * – если в сечении дитригон;
- тетрагональной – в сечении квадрат (тетрагон);
- дитетрагональной * – в сечении дитетрагон;
- гексагональной – в сечении шестиугольник (гексагон);
- дигексагональной* – в сечении дигексагон.
- Пирамида – простая форма состоит из нескольких равных граней, пересекающих координатную ось в одной точке; в зависимости от формы сечения (основания) также могут быть (Приложение 1, ряд III):
- ромбической – в сечении ромб;
- тригональной – если в сечении треугольник (тригон);
- дитригональной – если в сечении дитригон;
- тетрагональной – в сечении квадрат (тетрагон);
- дитетрагональной – в сечении дитетрагон;
- гексагональной – в сечении шестиугольник (гексагон);
- дигексагональной – в сечении дигексагон.
- Бипирамида – простая форма, которую можно представить как удвоенную пирамиду, состоит из нескольких граней, пересекающих координатную ось в двух точках, реализуется в видах симметрии, которые имеют горизонтальную плоскость симметрии (Приложение 1, ряд IV). Бипирамиды, как призмы и пирамиды могут быть ромбическими, тригональными, дитригональными, тетрагональными, дитетрагональными, гексагональными и дигексагональными.
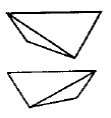
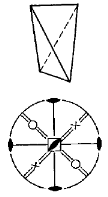
- Тетраэдр – простая форма, грани которой имеют форму треугольников и замыкают пространство, пересекают координатную ось в двух точках. Если грани в форме косоугольных треугольников, то тетраэдр ромбический (низшая категория) рис.Рисунок 7,а, если в форме равнобедренных – то тетраэдр тетрагональный (средняя категория, тетрагональная сингония) рис.Рисунок 7,б, если грани – равносторонние треугольники – тетраэдр (высшая категория).
| 
б
|
а
|
Рисунок 7 – Простая форма – тетраэдр, а – ромбический, б – тетрагональный
- Ромбоэдр – простая форма, состоящая из 6 граней, пересекающих главную ось в двух точках. Грани имеют форму ромба, три верхние и три нижние, причем нижние грани расположены симметрично между двумя верхними (рис.
- Рисунок 8,а).
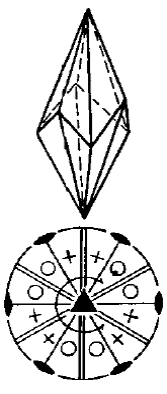
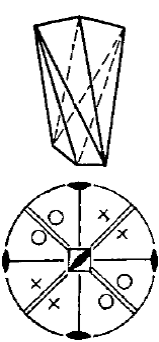
- Скаленоэдр – простая форма, грани которой имеют форму неравносторонних треугольников, пересекают главную ось в двух точках, пара нижних граней расположены симметрично между двумя парами верхних. Скаленоэдры могут быть тригональными (рис.
- Рисунок 8 ,б) и тетрагональными (рис.
-Рисунок 8 ,в).
а
|  б б
|  в в
|
Рисунок 8 – Простые формы средней категории: а – ромбоэдр, б – тригональный скаленоэдр, тетрагональный скаленоэдр
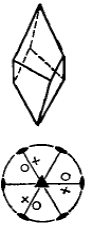
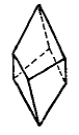
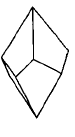
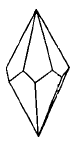
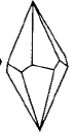
- Трапецоэдр – простая форма, грани которой имеют форму четырехугольника с двумя равными смежными сторонами, пересекают главную ось в двух точках (рис.Рисунок 9). Трапецоэдры могут быть тригональными (а,б), тетрагональными (в,г) и гексагональными (д,е), а также левыми и правыми.
левый
 а а
|
 правый
б правый
б
|
 правый
в правый
в
|
левый 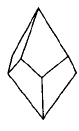 г
г
|
 правый
д правый
д
|
 левый
е левый
е
|
Рисунок 9 – Простые формы средней категории. Трапецоэдры: а, б – тригональный, в,г - тетрагональный, д,е – гексагональный
. В кристаллах кубической сингонии описанные выше простые формы не могут присутствовать. Всего имеется 15 простых форм, которые принадлежат только кристаллам кубической сингонии. Мы рассмотрим пять главных, а остальные являются производными от них. В высшей категории основные простые формы куб (гексаэдр), октаэдр и тетраэдр рис.Рисунок 10 и ромбододекаэдр и пентагондодекаэдр рис.Рисунок 11. Остальные можно получить из основных удвоением, утроением и ушестирением их граней.
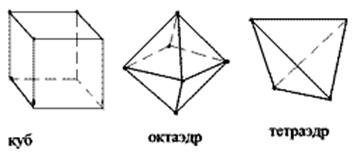
Рисунок 10 – Основные простые формы кубической сингонии
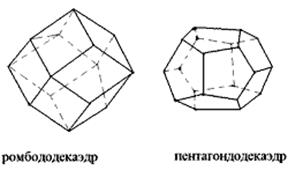
Рисунок 11 - Основные простые формы кристаллов высшей категории
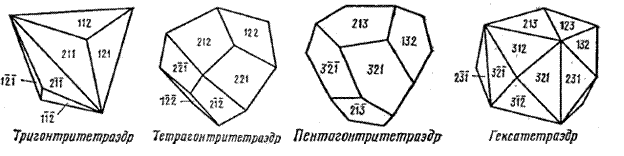
- Кубический тетраэдр - простая форма, образованная четырьмя равными равносторонними треугольными гранями, перпендикулярными осям 3-го порядка. «Надстраивая» на гранях тетраэдра по три треугольника, четырехугольника, пятиугольника получаем тригонтритетраэдр, тетрагонтритетраэдр и пентагонтритетраэдр соответственно. Если на грани тетраэдра надстроить шесть треугольников, то получим гексатетраэдр.
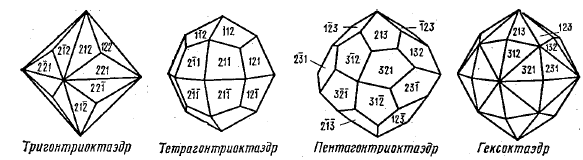
- Октаэдр (от греч."окта"- восемь,"эдр"- грань) - простая форма, образованная восемью равными равносторонними треугольными попарно параллельными гранями, перпендикулярными осям третьего порядка (L3). Надстраивая на гранях октаэдра, аналогично тетраэдру по три треугольника, четырех- или пятиугольника получим следующие простые формы: тригонтриоктаэдр, тетрагонтриоктаэдр или пентагонтриоктаэдр и гексаоктаэдр (шесть треугольников на каждой грани октаэдра).
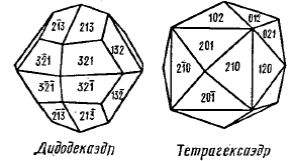
- Куб (гексаэдр) - простая форма, образованная шестью равными попарно параллельными квадратными гранями, образующими друг с другом углы 90о. Грани куба перпендикулярны осям четвертого порядка (L4). Надстраивая на гранях куба правильные четырехскатные крыши получим тетрагексаэдр,
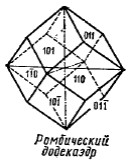
- Ромбододекаэдр (от греч."додека" - двенадцать) - простая форма, образованная 12 равными гранями, имеющими форму ромба. Ромбододекаэдр можно «получить» из куба притупляя его ребра.
- Пентагондодекаэдр (от греч."пента"- пять) - закрытая простая форма, которая состоит из 12 равных граней, имеющих форму неправильных пятиугольников. Удваивая каждую грань пентагондодекаэдра получим дидодекаэдр. Остальные простые формы кристаллов высшей категории приведены в Приложение 2.
В кристалле могут присутствовать одна или несколько простых форм. Сочетание нескольких простых форм называется комбинацией. Простые формы могут быть закрытыми и открытыми:
- Закрытыми называют такие формы, грани которых полностью замыкают заключенное между ними пространство, как, например, тетраэдры, дипирамиды, ромбоэдры, трапецоэдры, скаленоэдры, все простые формы высшей категории;
- Открытые простые формы (например, моноэдр, пинакоид, призма, пирамида и т.д.) не замыкают пространство и не могут существовать самостоятельно, а только в комбинациях. Например, призма + пинакоид.
Рекомендуемая литература:
1. Шаскольская М.П. Кристаллография. М., 1984.
2. Бокий Г.Б. Кристаллохимия. М., 1971.
Приложение 1
Приложение 2
[1] ГАЮИ (Аюи) Рене Жюст (1743-1822), французский кристаллограф и минералог, иностранный почетный член Петербургской АН (1806). Открыл один из основных законов кристаллографии (закон Гаюи).
[2] ШУБНИКОВ Алексей Васильевич (1887-1970), российский физик, академик АН СССР (1953), Герой Социалистического Труда (1967). Основатель и 1-й директор Института кристаллографии АН СССР (1944-62, ныне имени Шубникова). Труды по симметрии, физике и росту кристаллов. Вывел 58 точечных кристаллографических групп антисимметрии (т. н. шубниковские группы). Под руководством Шубникова организовано производство синтетических кристаллов. Государственная премия СССР (1947, 1950)
[3] БЕЛОВ Николай Васильевич (1891-1982), кристаллограф и геохимик, академик АН СССР (1953), Герой Социалистического Труда (1969). Фундаментальные труды по теории плотнейшей упаковки атомов в кристаллах, кристаллохимии силикатов, методам расшифровки структур минералов; под руководством Белова выяснена структура св. 100 силикатов и их аналогов. Ленинская премия (1974), Государственная премия СССР (1952), Золотая медаль им. Ломоносова АН СССР (1965)
[4] СТЕНОН (Стено, Стенсен) (Steno, Steensen) Николай (Николаус, Нильс) (1638-86), датский естествоиспытатель, один из основоположников геотектоники. Открыл проток околоушной слюнной железы (1660), описал строение мышц.
[5] ЛАУЭ (Laue) Макс фон (1879-1960), немецкий физик, иностранный член-корреспондент РАН (1924) и иностранный почетный член РАН АН СССР (1929). Разработал теорию дифракции рентгеновских лучей на кристаллах и предложил метод, с помощью которого она была открыта (1912). Труды по сверхпроводимости, теории относительности квантовой теории, атомной физике, истории физики. Нобелевская премия (1914).
[6] БРАВЭ (Bravais) Огюст (1811-63), французский кристаллограф. Положил начало геометрической теории пространственных решеток кристаллов (решетки Бравэ).
* - такие расположения осей симметрии не реализуются ни в одном виде симметрии
[8] Более подробно о стереографических проекциях см. §5 М.П.Шаскольская Кристаллография учеб.пособие для втузов – М.:Высш.шк., 1984.
[9] Единичное (особое) направление – это единственное, неповторяющееся в многограннике направление.
* подробнее доказательство см. §4 Шаскольская М.П. Кристаллография
[10] ВЕЙС Пьер Эрнест (1865-1940), французский физик. В 1907 высказал гипотезу о существовании в ферромагнетиках внутреннего магнитного поля (молекулярное поле Вейса) и областей самопроизвольной намагниченности. Один из авторов закона Кюри — Вейса. Открыл магнетокалорический эффект.
* координатные, элементы симметрии, проходящие вдоль координатных плоскостей, диагональные - по биссектрисам углов между ними.
* дитригональные, дитетрагональные и дигексагональныепростые формы реализуюьмя только в планальных видах симметрии, в которых есть диагональные плоскости.



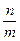 , n/m - ось симметрии n-го порядка и перпендикулярная ей плоскость симметрии.
, n/m - ось симметрии n-го порядка и перпендикулярная ей плоскость симметрии.

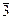 (ось 3-го порядка и центр симметрии дают ось инверсии 3 го порядка);
(ось 3-го порядка и центр симметрии дают ось инверсии 3 го порядка);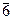 (ось 3-го порядка и перпендикулярная плоскость дают ось инверсии 6 го порядка).
(ось 3-го порядка и перпендикулярная плоскость дают ось инверсии 6 го порядка).

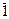 C
C 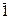









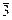 C
C 



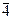
 L4PC
4/m
C4h
L4PC
4/m
C4h


 Li42L22P
Li42L22P
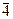 m
D2d
m
D2d



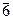
 L6PC
6/m
C6h
L6PC
6/m
C6h


 Li63L23P
Li63L23P
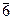 m2)
D3h
m2)
D3h





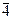 3m
Td
3m
Td




 б
б
 в
в
 а
а
 правый
б
правый
б
 правый
в
правый
в
 г
г
 правый
д
правый
д
 левый
е
левый
е










