Элементарное изложение отдельных фрагментов теории подгрупповых функторов
Исполнитель:
Студентка группы М-42
Ларченко А.Ю.
Научный руководитель:
Канд. физ-мат. наук, доцент
Зверева Т.Е.
Гомель 2006
Содержание
Введение
Перечень условных обозначений
1. Общие определения и обозначения
2. Используемые результаты
3. Определения и основные примеры подгрупповых функторов
4. Решетки подгрупповых функторов
5. Классы групп с заданными решетками подгрупповых функторов
Заключение
Список использованных источников
Введение
Согласно теореме о соответствии между подгруппами основной группы, содержащие нормальную подгруппу 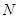 и подгруппами из факторуппы
и подгруппами из факторуппы  существует взаимнооднозначное соответствие, при котором нормальным подгруппам соответствуют нормальные подгруппы, субнормальным подгруппам соответствуют субнормальные и т.д.
существует взаимнооднозначное соответствие, при котором нормальным подгруппам соответствуют нормальные подгруппы, субнормальным подгруппам соответствуют субнормальные и т.д.
Этот факт лежит в основе следующего определения, введеного в монографии А.Н. Скибы "Алгебра формаций." (Мн.: Беларуская навука, 1997).
Пусть  некоторый класс групп. Составим с каждой группой
некоторый класс групп. Составим с каждой группой  некоторую систему ее подгрупп
некоторую систему ее подгрупп  . Будем говорить, что
. Будем говорить, что  - подгрупповой
- подгрупповой  -функтор или подгрупповой функтор на
-функтор или подгрупповой функтор на  , если выполняются следующие условия:
, если выполняются следующие условия:
1)  для всех
для всех  ;
;
2) для любого эпиморфизма  , где А,
, где А,  и для любых групп
и для любых групп  и
и  имеет место
имеет место  и
и 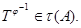
Значение этого понятия связано прежде всего с тем, что подгрупповой функтор выделяет в группе те системы подгрупп, которые инвариантны относительно гомоморфизма и поэтому удобны при проведении индуктивных рассуждений.
Целью данной дипломной работы является элементарное изложение отдельных фрагментов теории подгрупповых функтороф, доступное для понимания в рамках специальных курсов математических факультетов.
Дипломная работа состоит из введения, общей части, включающей 5 параграфов, заключения и списка используемой литературы.
В первом параграфе приводятся общие определения и обозначения.
Во втором параграфе даются те известные результаты теории групп, которые используются в основном тексте дипломной работы.
Третий параграф посвящен изучению основных понятий подгрупповых функторов и рассмотрению примеров. Здесь из различных источников собраны и систематизированы основные определения и примеры подгрупповых функторов.
В параграфе четыре систематизирован теоретический материал по теме "Решетки подгрупповых функторов".
Параграф пять изучает свойства конечных групп в зависимости от свойств соответствующих решеток подгрупповых функторов.
Используемые результаты
Теорема 1.1 (Теорема о соответствии) Пусть  - нормальная подгруппа группы
- нормальная подгруппа группы  . Тогда:
. Тогда:
( 1) если  - подгруппа группы
- подгруппа группы  и
и  , то
, то  - подгруппа факторгруппы
- подгруппа факторгруппы  ;
;
(2) каждая подгруппа факторгруппы  имеет вид
имеет вид 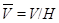 , где
, где  - подгруппа группы
- подгруппа группы  и
и  ;
;
(3) отображение  является биекцией множества S
является биекцией множества S 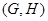 на множество S
на множество S  ;
;
(4) если  S
S  , то
, то  - нормальная подгруппа группы
- нормальная подгруппа группы 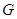 тогда и только тогда, когда
тогда и только тогда, когда  - нормальная подгруппа факторгруппы
- нормальная подгруппа факторгруппы  .
.
Лемма 1.2 Пусть  - гомоморфизм группы
- гомоморфизм группы  в группу
в группу 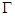 . Тогда:
. Тогда:
( 1) единичный элемент  группы
группы  переходит в единичный элемент
переходит в единичный элемент  группы
группы  , т.е.
, т.е.  ;
;
(2) обратный элемент переходит в обратный, т.е.  для всех
для всех 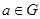 ;
;
(3) образ гомоморфизма является подгруппой группы  , т.е.
, т.е.  ;
;
(4) ядро гомоморфизма является нормальной подгруппой группы 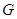 , т.е.
, т.е.  ;
;
(5) тогда и только тогда  где
где  когда
когда  .
.
Лемма 1.3 Пусть  - гомоморфизм группы
- гомоморфизм группы  в группу
в группу 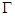 . Тогда:
. Тогда:
( 1) если  , то
, то 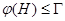 ;
;
(2) если  , то
, то  ;
;
(3) если подмножества 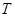 и
и  сопряжены в
сопряжены в  , то
, то  и
и  сопряжены в
сопряжены в  .
.
Теорема 1.4 (Основная теорема о гомоморфизме) При гомоморфизме групп факторгруппа по ядру изоморфна образу, т.е. если  - гомоморфизм, то
- гомоморфизм, то  .
.
Теорема 1.5 (первая о изоморфизме) Пусть  - нормальная подгруппа группы
- нормальная подгруппа группы  . Тогда для любой подгруппы
. Тогда для любой подгруппы  пересечение
пересечение  является нормальной подгруппой в подгруппе
является нормальной подгруппой в подгруппе  , а отображение
, а отображение 
является изоморфизмом групп  и
и 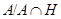 .
.
Теорема 1.6 (вторая о изоморфизме) Если  и
и  - нормальные подгруппы группы
- нормальные подгруппы группы  , причем
, причем  , то
, то  изоморфна
изоморфна  .
.
Лемма 3.1 Пусть  - формация,
- формация,  . Тогда
. Тогда

Лемма 20.6. Пусть 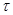 - подгрупповой функтор и
- подгрупповой функтор и  - группа. Если
- группа. Если  и
и  , тогда
, тогда  .
.
Лемма 20.7. Пусть  ,
,  - элементарно абелевы
- элементарно абелевы  -группы с
-группы с 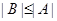 . Тогда
. Тогда  имеет подгруппу
имеет подгруппу  такую, что
такую, что  .
.
Теорема. Пусть  - такой набор конгруэнций
- такой набор конгруэнций  -алгебры A, что
-алгебры A, что  . Пусть
. Пусть  прямое произведение факторалгебр
прямое произведение факторалгебр  и
и 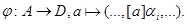
Тогда  - мономорфизм алгебры
- мономорфизм алгебры  в алгебру
в алгебру  и
и  входит подпрямо в
входит подпрямо в  .
.
Теорема 20.8. Пусть 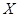 - конечное многообразие локально конечных групп, причем каждая группа из
- конечное многообразие локально конечных групп, причем каждая группа из 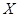 либо счетна, либо конечна. Тогда в том и только в том случае решетка
либо счетна, либо конечна. Тогда в том и только в том случае решетка 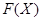 является цепью, когда существует такое простое число
является цепью, когда существует такое простое число  , что каждая группа в
, что каждая группа в 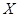 является элементарно абелевой
является элементарно абелевой  -группой.
-группой.
Теорема 20.9. Пусть  - конечная группа и
- конечная группа и  - конечное многообразие, порожденное
- конечное многообразие, порожденное  . Тогда в том и только в том случае
. Тогда в том и только в том случае 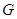 является элементарной абелевой
является элементарной абелевой  -группой, когда решетка
-группой, когда решетка  является цепью.
является цепью.
Лемма 24.9 Пусть 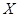 - наследственный гомоморф конечных групп. Пусть
- наследственный гомоморф конечных групп. Пусть 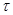 - замкнутый подгрупповой функтор на
- замкнутый подгрупповой функтор на 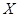 Пусть
Пусть  - нильпотентная группа в
- нильпотентная группа в 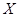 и
и 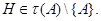 Предположим, что
Предположим, что  , где
, где  - простое число. Пусть
- простое число. Пусть  - нильпотентная группа в
- нильпотентная группа в 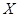 такая, что
такая, что  и
и 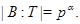 Тогда
Тогда 
Лемма 24.10 Пусть 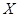 - наследственный гомоморф конечных нильпотентных групп и
- наследственный гомоморф конечных нильпотентных групп и  Пусть
Пусть  Если
Если 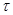 - идемпотент в
- идемпотент в  , удовлетворяющий условию
, удовлетворяющий условию  и
и 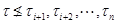 , где
, где 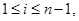 тогда
тогда 
Теорема 24.11 Пусть 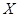 - конечное многообразие групп. И пусть каждая группа в
- конечное многообразие групп. И пусть каждая группа в 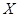 конечная. Тогда ширина
конечная. Тогда ширина  решетки
решетки  всех идемпотентов в
всех идемпотентов в 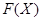 конечна и
конечна и  в том и только в том случае, когда
в том и только в том случае, когда 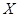 состоит из нильпотентных групп и
состоит из нильпотентных групп и 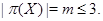
3. Определения и основные примеры подгрупповых функторов
Пусть  некоторый класс групп. Составим с каждой группой
некоторый класс групп. Составим с каждой группой  некоторую систему ее подгрупп
некоторую систему ее подгрупп  . Будем говорить, что
. Будем говорить, что 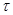 - подгрупповой
- подгрупповой  -функтор или подгрупповой функтор на
-функтор или подгрупповой функтор на  , если выполняются следующие условия: 1)
, если выполняются следующие условия: 1)  для всех
для всех 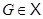 ;
;
2) для любого эпиморфизма  , где А,
, где А,  и для любых групп
и для любых групп  и
и  имеет место
имеет место  и
и 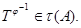
Подгрупповой  -функтор
-функтор 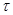 называется:
называется:
1) замкнутым, если для любых двух групп 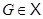 и
и  имеет место
имеет место 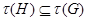 ;
;
2) тривиальным, если для любой группы 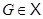 имеет место
имеет место
 ;
;
3) единичным, если для любой группы 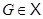 система
система  состоит из всех подгрупп группы G.
состоит из всех подгрупп группы G.
Тривиальный подгрупповой  -функтор обозначается символом
-функтор обозначается символом  , а единичный - символом
, а единичный - символом  .
.
Если  и
и  - подгрупповой
- подгрупповой 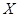 -функтор, то
-функтор, то  - такой подгрупповой
- такой подгрупповой  -функтор, что
-функтор, что  для всех
для всех  . Такой функтор называется ограничением функтора
. Такой функтор называется ограничением функтора  на классе
на классе 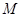 .
.
Рассмотрим несколько примеров подгрупповых функторов. В случае, когда  - класс всех групп, подгрупповые
- класс всех групп, подгрупповые  -функторы мы будем называть просто подгрупповыми функторами.
-функторы мы будем называть просто подгрупповыми функторами.
Пример 1. Пусть для любой группы  ,
, 


Понятно, что  - замкнутый подгрупповой функтор. Для обозначения такого подгруппового функтора мы применяем запись
- замкнутый подгрупповой функтор. Для обозначения такого подгруппового функтора мы применяем запись  .
.
Пример 2. Пусть  - совокупность всех нормальных подгрупп группы
- совокупность всех нормальных подгрупп группы  для каждой группы
для каждой группы  . Такой функтор в общем случае замкнутым не является.
. Такой функтор в общем случае замкнутым не является.
Пример 3. Пусть  - произвольное натуральное число. Для каждой группы
- произвольное натуральное число. Для каждой группы  через
через  обозначим совокупность всех таких подгрупп
обозначим совокупность всех таких подгрупп  , для которых
, для которых  . Понятно, что
. Понятно, что  - подгрупповой
- подгрупповой 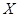 -функтор. Для обозначения такого функтора мы будем применять запись
-функтор. Для обозначения такого функтора мы будем применять запись  .
.
Пример 4. Пусть  - произвольное кардинальное число. И пусть для любой группы
- произвольное кардинальное число. И пусть для любой группы 





 .
.
Понятно, что такой подгрупповой функтор в общем случае не является замкнутым. Для обозначения такого функтора мы применяем запись  .
.
Если  - подгруппа группы
- подгруппа группы  , то символом
, то символом  обозначается мощность множества
обозначается мощность множества  .
.
Пример 5. Пусть 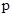 - простое число и пусть для любой группы
- простое число и пусть для любой группы 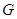 система
система  в
в  нет такой подгруппы
нет такой подгруппы  , что
, что  ,
, 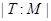 - натуральное число, взаимнопростое с
- натуральное число, взаимнопростое с  .
.
Покажем, что 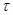 - подгрупповой функтор.
- подгрупповой функтор.
Действительно, пусть 
 и
и 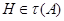 . Предположим, что
. Предположим, что 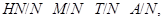
где 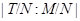 - натуральное число. Тогда
- натуральное число. Тогда  - натуральное число и
- натуральное число и 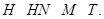
Следовательно, 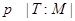 , и поэтому
, и поэтому  . Это означает, что
. Это означает, что  . Аналогично, мы видим, что если
. Аналогично, мы видим, что если 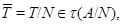
то  . Таким образом,
. Таким образом, 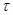 - подгрупповой функтор. Для обозначения такого подгруппового функтора мы используем запись
- подгрупповой функтор. Для обозначения такого подгруппового функтора мы используем запись  . Заметим, что если
. Заметим, что если 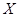 - некоторый класс конечных групп и
- некоторый класс конечных групп и  , то
, то  - замкнутый подгрупповой функтор.
- замкнутый подгрупповой функтор.
Пример 6. Пусть  . И пусть для каждой группы
. И пусть для каждой группы 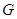 множество
множество  совпадает с совокупностью всех тех подгрупп из
совпадает с совокупностью всех тех подгрупп из  , индексы которых не делятся на числа из
, индексы которых не делятся на числа из  . Понятно, что
. Понятно, что 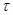 - замкнутый подгрупповой функтор. Для обозначения такого функтора мы будем применять запись
- замкнутый подгрупповой функтор. Для обозначения такого функтора мы будем применять запись  .
.
Напомним, что подгруппа  группы
группы  называется абнормальной в
называется абнормальной в 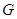 , если всегда из
, если всегда из  следует, что
следует, что  .
.
Пример 7. Пусть для любой группы  множество
множество 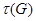 совпадает с совокупностью всех абнормальных подгрупп группы
совпадает с совокупностью всех абнормальных подгрупп группы  . Легко видеть, что
. Легко видеть, что 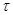 - незамкнутый подгрупповой функтор. Для обозначения такого функтора мы будем применять запись
- незамкнутый подгрупповой функтор. Для обозначения такого функтора мы будем применять запись  .
.
Пример 8. Пусть  - произвольный класс групп. Подгруппа
- произвольный класс групп. Подгруппа  группы
группы 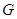 называется
называется  - абнормальной в
- абнормальной в  , если выполняется одно из следующих двух условий:
, если выполняется одно из следующих двух условий:
1)  ;
;
2)  и для любых двух подгрупп
и для любых двух подгрупп  и
и  из
из  , где
, где  и
и  - максимальная подгруппа в
- максимальная подгруппа в  имеет место
имеет место  .
.
Легко видеть, если группа  разрешима, то ее подгруппа
разрешима, то ее подгруппа  абнормальна в
абнормальна в 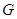 тогда и только тогда, когда она
тогда и только тогда, когда она  -абнормальна в
-абнормальна в  .
.
Сопоставляя каждой группе  множество всех ее
множество всех ее  -абнормальных подгрупп
-абнормальных подгрупп 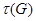 , получаем подгрупповой функтор, для которого мы будем применять запись
, получаем подгрупповой функтор, для которого мы будем применять запись  .
.
Пример 9. Подгруппа  группы
группы  называется
называется  -субнормальной в
-субнормальной в 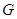 , если выполняется одно из следующих двух условий:
, если выполняется одно из следующих двух условий:
1)  ;
;
2)  и в
и в  имеется такая цепь подгрупп
имеется такая цепь подгрупп  где
где  - максимальная в
- максимальная в  подгруппа, содержащая
подгруппа, содержащая  ,
,  .
.
Пусть  - некоторая непустая формация и для каждой группы
- некоторая непустая формация и для каждой группы  система
система  состоит из всех
состоит из всех  -субнормальных в
-субнормальных в 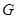 подгрупп.
подгрупп.
Покажем, что 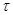 - подгрупповой функтор. Пусть
- подгрупповой функтор. Пусть 
 -субнормальна в
-субнормальна в  . И пусть
. И пусть  и
и  - такие члены цепи (1), что
- такие члены цепи (1), что  , где
, где  - нормальная в
- нормальная в  подгруппа.
подгруппа.
Покажем, что 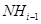 - максимальная подгруппа в
- максимальная подгруппа в 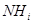 . Допустим, что
. Допустим, что  для некоторой подгруппы
для некоторой подгруппы  . Тогда поскольку
. Тогда поскольку  максимальна в
максимальна в 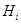 , то либо
, то либо  , либо
, либо  .
.
Пусть имеет место первое. Тогда поскольку  , то
, то  . Противоречие. Значит,
. Противоречие. Значит,  , т.е.
, т.е.  . Поэтому
. Поэтому  . Противоречие. Итак, ряд
. Противоречие. Итак, ряд  таков, что в нём для любого
таков, что в нём для любого  имеет место одно из двух условий:
имеет место одно из двух условий:
1)  ;
;
2)  - максимальная подгруппа в
- максимальная подгруппа в  . He теряя общности, мы можем считать, что все члены ряда (2) различны. Заметим, что поскольку
. He теряя общности, мы можем считать, что все члены ряда (2) различны. Заметим, что поскольку  то
то 
Итак,  -
-  -субнормальная подгруппа в
-субнормальная подгруппа в  . Понятно также, что если
. Понятно также, что если  -
-  -субнормальная подгруппа в
-субнормальная подгруппа в  , то
, то  -
-  -субнормальная подгруппа в
-субнормальная подгруппа в  . Таким образом,
. Таким образом, 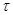 - подгрупповой функтор. Для обозначения такого функтора мы будем применять запись
- подгрупповой функтор. Для обозначения такого функтора мы будем применять запись  .
.
Класс групп называется гомоморфом, если он содержит все гомоморфные образы всех своих групп. Гомоморф конечных групп  называется формацией, если каждая конечная группа
называется формацией, если каждая конечная группа 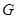 обладает наименьшей по включению нормальной подгруппой (обозначаемой символом
обладает наименьшей по включению нормальной подгруппой (обозначаемой символом  ) со свойством
) со свойством 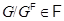 .
.
Лемма 3.1 Пусть  - формация,
- формация,  . Тогда
. Тогда 
Доказательство. Пусть 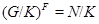 . Тогда
. Тогда 
Отсюда следует, что  . С другой стороны, поскольку
. С другой стороны, поскольку  - гомоморф, то
- гомоморф, то 
Откуда получаем  . Из
. Из  и
и 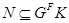 следует равенство
следует равенство  .
.
Лемма доказана.
Пример 10. Пусть 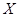 - некоторый класс конечных групп и
- некоторый класс конечных групп и  - формация. Пусть для любой группы
- формация. Пусть для любой группы 

Покажем, что 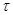 - подгрупповой
- подгрупповой 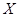 - функтор.
- функтор.
Действительно, пусть  и
и  . Тогда
. Тогда 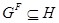 , и поэтому, согласно лемме 3.1, мы имеем
, и поэтому, согласно лемме 3.1, мы имеем 
Следовательно,  . Аналогично, если
. Аналогично, если 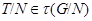 , то
, то  . Следовательно,
. Следовательно, 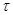 - подгрупповой
- подгрупповой 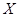 -функтор. Для обозначения такого функтора мы применяем запись
-функтор. Для обозначения такого функтора мы применяем запись  .
.
Пример 11. Для каждой группы  через
через 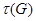 обозначим совокупность всех абнормальных максимальных подгрупп из
обозначим совокупность всех абнормальных максимальных подгрупп из  . Понятно, что
. Понятно, что 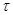 - подгрупповой функтор. Для обозначения такого функтора мы будем применять запись
- подгрупповой функтор. Для обозначения такого функтора мы будем применять запись  .
.
Заключение
Отметим, что теория подгрупповых функторов уже нашла много примениний при иследовании внутреннего строения конечных групп [1, 2, 3, 4]. Но еще один аспект применения подгупповых функторов состоит в сопоставлении группе некоторой решетки подгупповых функторов свойства которой тесно связаны со свойствами самой группы. Это позволяет использовать строение группы в зависимости от условий налогаемых на соответствующую решетку подгупповых функторов.
Следует отметить также, что используя понятие подгуппового функтора можно строить новые типы решеток, что указывает на полезность этого понятия и для теории решеток.
Элементарное изложение отдельных фрагментов теории подгрупповых функторов
Исполнитель:
Студентка группы М-42
Ларченко А.Ю.
Научный руководитель:
Канд. физ-мат. наук, доцент
Зверева Т.Е.
Гомель 2006
Содержание
Введение
Перечень условных обозначений
1. Общие определения и обозначения
2. Используемые результаты
3. Определения и основные примеры подгрупповых функторов
4. Решетки подгрупповых функторов
5. Классы групп с заданными решетками подгрупповых функторов
Заключение
Список использованных источников
Введение
Согласно теореме о соответствии между подгруппами основной группы, содержащие нормальную подгруппу 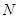 и подгруппами из факторуппы
и подгруппами из факторуппы  существует взаимнооднозначное соответствие, при котором нормальным подгруппам соответствуют нормальные подгруппы, субнормальным подгруппам соответствуют субнормальные и т.д.
существует взаимнооднозначное соответствие, при котором нормальным подгруппам соответствуют нормальные подгруппы, субнормальным подгруппам соответствуют субнормальные и т.д.
Этот факт лежит в основе следующего определения, введеного в монографии А.Н. Скибы "Алгебра формаций." (Мн.: Беларуская навука, 1997).
Пусть  некоторый класс групп. Составим с каждой группой
некоторый класс групп. Составим с каждой группой  некоторую систему ее подгрупп
некоторую систему ее подгрупп  . Будем говорить, что
. Будем говорить, что  - подгрупповой
- подгрупповой  -функтор или подгрупповой функтор на
-функтор или подгрупповой функтор на  , если выполняются следующие условия:
, если выполняются следующие условия:
1)  для всех
для всех  ;
;
2) для любого эпиморфизма  , где А,
, где А,  и для любых групп
и для любых групп  и
и  имеет место
имеет место  и
и 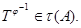
Значение этого понятия связано прежде всего с тем, что подгрупповой функтор выделяет в группе те системы подгрупп, которые инвариантны относительно гомоморфизма и поэтому удобны при проведении индуктивных рассуждений.
Целью данной дипломной работы является элементарное изложение отдельных фрагментов теории подгрупповых функтороф, доступное для понимания в рамках специальных курсов математических факультетов.
Дипломная работа состоит из введения, общей части, включающей 5 параграфов, заключения и списка используемой литературы.
В первом параграфе приводятся общие определения и обозначения.
Во втором параграфе даются те известные результаты теории групп, которые используются в основном тексте дипломной работы.
Третий параграф посвящен изучению основных понятий подгрупповых функторов и рассмотрению примеров. Здесь из различных источников собраны и систематизированы основные определения и примеры подгрупповых функторов.
В параграфе четыре систематизирован теоретический материал по теме "Решетки подгрупповых функторов".
Параграф пять изучает свойства конечных групп в зависимости от свойств соответствующих решеток подгрупповых функторов.



 и подгруппами из факторуппы
и подгруппами из факторуппы  существует взаимнооднозначное соответствие, при котором нормальным подгруппам соответствуют нормальные подгруппы, субнормальным подгруппам соответствуют субнормальные и т.д.
существует взаимнооднозначное соответствие, при котором нормальным подгруппам соответствуют нормальные подгруппы, субнормальным подгруппам соответствуют субнормальные и т.д. некоторый класс групп. Составим с каждой группой
некоторый класс групп. Составим с каждой группой  некоторую систему ее подгрупп
некоторую систему ее подгрупп  . Будем говорить, что
. Будем говорить, что  - подгрупповой
- подгрупповой  для всех
для всех  , где А,
, где А,  и для любых групп
и для любых групп  и
и  имеет место
имеет место  и
и 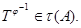
 - нормальная подгруппа группы
- нормальная подгруппа группы  . Тогда:
. Тогда: - подгруппа группы
- подгруппа группы  , то
, то  - подгруппа факторгруппы
- подгруппа факторгруппы  ;
;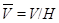 , где
, где  - подгруппа группы
- подгруппа группы  ;
; является биекцией множества S
является биекцией множества S 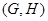 на множество S
на множество S  ;
; S
S  , то
, то  - нормальная подгруппа группы
- нормальная подгруппа группы 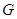 тогда и только тогда, когда
тогда и только тогда, когда  - нормальная подгруппа факторгруппы
- нормальная подгруппа факторгруппы  .
. - гомоморфизм группы
- гомоморфизм группы 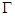 . Тогда:
. Тогда: группы
группы  группы
группы  , т.е.
, т.е.  ;
; для всех
для всех 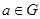 ;
; ;
; ;
; где
где  когда
когда  .
. , то
, то 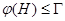 ;
; , то
, то  ;
;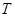 и
и  сопряжены в
сопряжены в  и
и  сопряжены в
сопряжены в  .
. .
. пересечение
пересечение  является нормальной подгруппой в подгруппе
является нормальной подгруппой в подгруппе 
 и
и 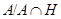 .
. , то
, то  изоморфна
изоморфна  .
. - формация,
- формация,  . Тогда
. Тогда
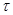 - подгрупповой функтор и
- подгрупповой функтор и  и
и  , тогда
, тогда  .
. - элементарно абелевы
- элементарно абелевы  -группы с
-группы с 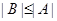 . Тогда
. Тогда  имеет подгруппу
имеет подгруппу  .
. - такой набор конгруэнций
- такой набор конгруэнций  -алгебры A, что
-алгебры A, что  . Пусть
. Пусть  прямое произведение факторалгебр
прямое произведение факторалгебр  и
и 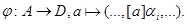
 - мономорфизм алгебры
- мономорфизм алгебры  и
и  входит подпрямо в
входит подпрямо в 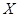 - конечное многообразие локально конечных групп, причем каждая группа из
- конечное многообразие локально конечных групп, причем каждая группа из 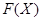 является цепью, когда существует такое простое число
является цепью, когда существует такое простое число  является цепью.
является цепью.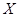 и
и 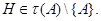 Предположим, что
Предположим, что  , где
, где  - нильпотентная группа в
- нильпотентная группа в  и
и 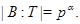 Тогда
Тогда 
 Пусть
Пусть  Если
Если  , удовлетворяющий условию
, удовлетворяющий условию  и
и 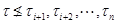 , где
, где 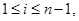 тогда
тогда 
 решетки
решетки  всех идемпотентов в
всех идемпотентов в  в том и только в том случае, когда
в том и только в том случае, когда 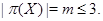
 некоторый класс групп. Составим с каждой группой
некоторый класс групп. Составим с каждой группой  некоторую систему ее подгрупп
некоторую систему ее подгрупп  . Будем говорить, что
. Будем говорить, что  -функтор или подгрупповой функтор на
-функтор или подгрупповой функтор на  для всех
для всех 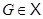 ;
; , где А,
, где А,  и для любых групп
и для любых групп  и
и  и
и 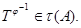
 имеет место
имеет место 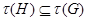 ;
; ;
; , а единичный - символом
, а единичный - символом  .
. и
и  - подгрупповой
- подгрупповой  - такой подгрупповой
- такой подгрупповой  -функтор, что
-функтор, что  для всех
для всех  . Такой функтор называется ограничением функтора
. Такой функтор называется ограничением функтора 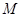 .
.


 .
. - совокупность всех нормальных подгрупп группы
- совокупность всех нормальных подгрупп группы  . Такой функтор в общем случае замкнутым не является.
. Такой функтор в общем случае замкнутым не является. - произвольное натуральное число. Для каждой группы
- произвольное натуральное число. Для каждой группы  обозначим совокупность всех таких подгрупп
обозначим совокупность всех таких подгрупп  , для которых
, для которых  . Понятно, что
. Понятно, что  .
.



 .
. .
. - подгруппа группы
- подгруппа группы  обозначается мощность множества
обозначается мощность множества  .
.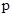 - простое число и пусть для любой группы
- простое число и пусть для любой группы  в
в  , что
, что  ,
, 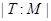 - натуральное число, взаимнопростое с
- натуральное число, взаимнопростое с  .
.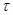 - подгрупповой функтор.
- подгрупповой функтор.
 и
и 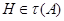 . Предположим, что
. Предположим, что 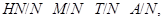
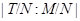 - натуральное число. Тогда
- натуральное число. Тогда  - натуральное число и
- натуральное число и 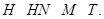
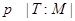 , и поэтому
, и поэтому  . Это означает, что
. Это означает, что  . Аналогично, мы видим, что если
. Аналогично, мы видим, что если 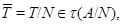
 . Таким образом,
. Таким образом,  . Заметим, что если
. Заметим, что если  , то
, то  - замкнутый подгрупповой функтор.
- замкнутый подгрупповой функтор. . И пусть для каждой группы
. И пусть для каждой группы  совпадает с совокупностью всех тех подгрупп из
совпадает с совокупностью всех тех подгрупп из  . Понятно, что
. Понятно, что  .
. следует, что
следует, что  .
.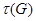 совпадает с совокупностью всех абнормальных подгрупп группы
совпадает с совокупностью всех абнормальных подгрупп группы 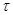 - незамкнутый подгрупповой функтор. Для обозначения такого функтора мы будем применять запись
- незамкнутый подгрупповой функтор. Для обозначения такого функтора мы будем применять запись  .
. ;
; и для любых двух подгрупп
и для любых двух подгрупп  и
и  и
и  - максимальная подгруппа в
- максимальная подгруппа в  .
. -абнормальна в
-абнормальна в  .
. где
где  - максимальная в
- максимальная в  подгруппа, содержащая
подгруппа, содержащая  ,
,  .
. система
система  состоит из всех
состоит из всех 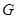 подгрупп.
подгрупп. -субнормальна в
-субнормальна в  и
и  , где
, где 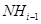 - максимальная подгруппа в
- максимальная подгруппа в 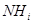 . Допустим, что
. Допустим, что  для некоторой подгруппы
для некоторой подгруппы  . Тогда поскольку
. Тогда поскольку 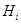 , то либо
, то либо  , либо
, либо  .
. , то
, то  . Противоречие. Значит,
. Противоречие. Значит,  . Поэтому
. Поэтому  . Противоречие. Итак, ряд
. Противоречие. Итак, ряд  таков, что в нём для любого
таков, что в нём для любого  имеет место одно из двух условий:
имеет место одно из двух условий: ;
; - максимальная подгруппа в
- максимальная подгруппа в  . He теряя общности, мы можем считать, что все члены ряда (2) различны. Заметим, что поскольку
. He теряя общности, мы можем считать, что все члены ряда (2) различны. Заметим, что поскольку  то
то 
 -
-  -
-  .
. называется формацией, если каждая конечная группа
называется формацией, если каждая конечная группа  ) со свойством
) со свойством 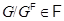 .
. . Тогда
. Тогда 
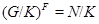 . Тогда
. Тогда 
 . С другой стороны, поскольку
. С другой стороны, поскольку 
 . Из
. Из  и
и 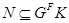 следует равенство
следует равенство  .
.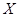 - некоторый класс конечных групп и
- некоторый класс конечных групп и 
 и
и  . Тогда
. Тогда 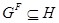 , и поэтому, согласно лемме 3.1, мы имеем
, и поэтому, согласно лемме 3.1, мы имеем 
 . Аналогично, если
. Аналогично, если 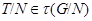 , то
, то  . Следовательно,
. Следовательно,  .
. через
через  .
.


