Сопоставляя классу конечных групп 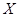 решетки
решетки 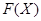 и
и 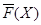 можно изучать свойства групп из
можно изучать свойства групп из 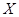 в зависимости от свойств решеток
в зависимости от свойств решеток 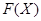 и
и 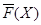 .
.
Лемма 20.6. Пусть 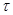 - подгрупповой функтор и
- подгрупповой функтор и 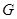 - группа. Если
- группа. Если 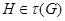 и
и  , тогда
, тогда 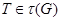 .
.
Доказательство. Если 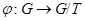 - канонический эпиморфизм
- канонический эпиморфизм 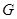 на
на 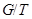 , то
, то 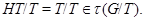
Так как 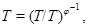 мы видим по определению подгрупповых функторов, что
мы видим по определению подгрупповых функторов, что 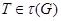 .
.
Лемма доказана.
Пусть 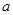 - элемент группы
- элемент группы 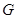 . Тогда если для некоторого натурального числа
. Тогда если для некоторого натурального числа 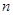 имеет место
имеет место 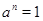 , то наименьшее натуральное число
, то наименьшее натуральное число 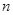 с таким свойством называется порядком элемента
с таким свойством называется порядком элемента 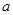 . Говорят, что
. Говорят, что 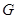 - группа экспоненты
- группа экспоненты 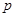 , если каждый ее неединичный элемент имеет порядок
, если каждый ее неединичный элемент имеет порядок 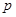 .
.
Пусть 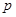 - простое число. Тогда группа
- простое число. Тогда группа 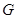 называется элементарно абелевой
называется элементарно абелевой 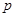 -группой, если
-группой, если 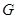 - абелева группа экспоненты
- абелева группа экспоненты  .
.
Лемма 20.7. Пусть 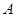 ,
, 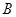 - элементарно абелевы
- элементарно абелевы  -группы с
-группы с 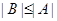 . Тогда
. Тогда 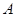 имеет подгруппу
имеет подгруппу  такую, что
такую, что 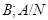 .
.
Доказательство. Нам необходимо рассмотреть лишь случай, когда 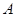 - бесконечная группа.
- бесконечная группа.
Пусть 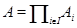 и
и 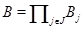 , где
, где 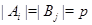 для всех
для всех 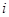 и
и 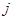 . Пусть
. Пусть 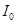 - подмножество в
- подмножество в 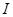 такое, что
такое, что 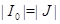 . И пусть
. И пусть 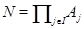 , где
, где 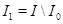 и
и 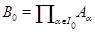 . Тогда ясно, что
. Тогда ясно, что 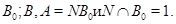
Следовательно, 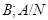 .
.
Лемма доказана.
Напомним, что класс групп называется наследственным, если он содержит все подгруппы всех своих групп. Класс групп называется конечным многообразием, если он наследственен, является гомоморфом и содержит прямое произведение (с конечным числом сомножителей) любых своих групп.
Пусть  - простое число, делящее порядок группы
- простое число, делящее порядок группы 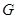 . Подгруппа
. Подгруппа 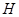 группы
группы 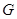 называется силовской
называется силовской  -подгруппой в
-подгруппой в 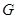 , если
, если 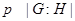 и
и 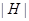 - степень числа
- степень числа 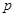 . Известная в теории групп теорема Силова утверждает, что для любого простого числа
. Известная в теории групп теорема Силова утверждает, что для любого простого числа  в любой конечной группе
в любой конечной группе 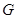 с
с 

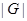 имеется силовская
имеется силовская 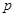 -подгруппа. Конечная группа
-подгруппа. Конечная группа 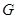 называется
называется  -группой, если ее порядок является степенью числа
-группой, если ее порядок является степенью числа  .
.
Обозначим через 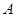 - класс всех конечных абелевых групп. Ввиду теоремы
- класс всех конечных абелевых групп. Ввиду теоремы
Теорема. Пусть 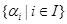 - такой набор конгруэнций
- такой набор конгруэнций 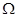 -алгебры A, что
-алгебры A, что 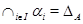 . Пусть
. Пусть 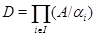 прямое произведение факторалгебр
прямое произведение факторалгебр 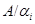 и
и 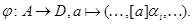
Тогда 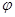 - мономорфизм алгебры
- мономорфизм алгебры 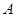 в алгебру
в алгебру 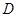 и
и 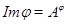 входит подпрямо в
входит подпрямо в 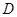 ., класс
., класс 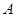 является формацией. Обычно вместо
является формацией. Обычно вместо 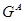 пишут
пишут 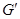 . Подгруппа
. Подгруппа 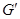 называется коммутантом группы
называется коммутантом группы 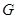 . В теории групп хорошо известно, что если
. В теории групп хорошо известно, что если 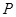 - конечная
- конечная  -группа, то
-группа, то 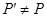 . Легко проверить, что если
. Легко проверить, что если 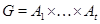 , то
, то 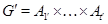
Теорема 20.8. Пусть 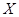 - конечное многообразие локально конечных групп, причем каждая группа из
- конечное многообразие локально конечных групп, причем каждая группа из 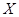 либо счетна, либо конечна. Тогда в том и только в том случае решетка
либо счетна, либо конечна. Тогда в том и только в том случае решетка 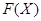 является цепью, когда существует такое простое число
является цепью, когда существует такое простое число 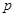 , что каждая группа в
, что каждая группа в 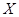 является элементарно абелевой
является элементарно абелевой  -группой.
-группой.
Доказательство. Мы сначала предположим, что каждая группа в 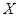 является элементарно абелевой
является элементарно абелевой  -группой. Тогда для каждого кардинального числа
-группой. Тогда для каждого кардинального числа 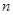 , мы полагаем
, мы полагаем 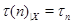 (см. пример 20.2). Понятно, что
(см. пример 20.2). Понятно, что 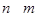 влечет, что
влечет, что 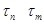 . Для доказательства того, что
. Для доказательства того, что 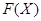 является цепью нам необходимо только показать, что для любого подгруппового функтора
является цепью нам необходимо только показать, что для любого подгруппового функтора 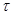 со свойством
со свойством 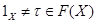 найдется кардинальное число
найдется кардинальное число 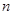 такое, что
такое, что 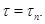
Предположим, что 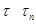 для всех кардинальных чисел
для всех кардинальных чисел 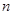 . Тогда
. Тогда 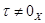 . Поскольку
. Поскольку 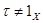 , то найдется группа
, то найдется группа 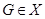 такая, что для некоторой ее подгруппы
такая, что для некоторой ее подгруппы 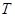 мы имеем
мы имеем 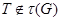 . Пусть
. Пусть 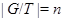 . Поскольку
. Поскольку 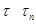 , найдется группа
, найдется группа 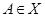 такая, что для некоторой ее подгруппы
такая, что для некоторой ее подгруппы 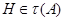 мы имеем
мы имеем 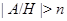 . По лемме 20.6, мы видим, что для всех подгрупп
. По лемме 20.6, мы видим, что для всех подгрупп 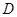 из
из 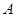 , удовлетворяющих условию
, удовлетворяющих условию 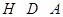 , мы имеем
, мы имеем 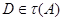 . Следовательно,
. Следовательно, 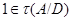 . Используя лемму 20.7, мы видим, что имеется подгруппа
. Используя лемму 20.7, мы видим, что имеется подгруппа 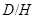 в группе
в группе 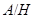 такая, что
такая, что 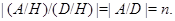
Но 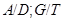 , и поэтому
, и поэтому 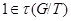 . Если
. Если 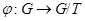 - канонический эпиморфизм, который отображает
- канонический эпиморфизм, который отображает 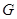 на
на 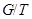 , то
, то 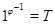 , и поэтому
, и поэтому 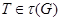 . Это противоречие показывает, что для некоторого кардинального числа
. Это противоречие показывает, что для некоторого кардинального числа 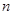 имеем место
имеем место 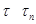 .
.
Так как 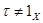 и так как каждая группа в
и так как каждая группа в 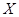 - либо конечна, либо счетна, то найдется натуральное число
- либо конечна, либо счетна, то найдется натуральное число 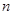 такое, что
такое, что 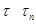 . Пусть
. Пусть 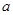 - наименьшее натуральное число такое, что
- наименьшее натуральное число такое, что 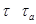 . Мы покажем, что
. Мы покажем, что 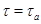 . Предположим, что
. Предположим, что 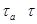 и пусть
и пусть 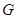 - группа из
- группа из 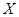 такая, что
такая, что 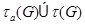 . В этом случае пусть
. В этом случае пусть 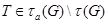 . Тогда
. Тогда 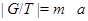 . Теперь, по выбору числа
. Теперь, по выбору числа 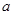 , мы имеем
, мы имеем 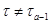 . Это означает, что найдется группа
. Это означает, что найдется группа 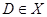 такая, что
такая, что 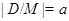 для некоторой подгруппы
для некоторой подгруппы 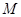 из
из 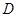 с
с 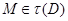 . Пусть
. Пусть  - подгруппа в
- подгруппа в 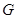 такая, что
такая, что 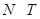 и
и 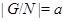 . Тогда
. Тогда 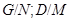 . Так как
. Так как 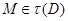 , мы имеем
, мы имеем 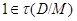 , и поэтому
, и поэтому 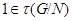 . Но тогда
. Но тогда 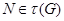 , и поэтому
, и поэтому 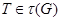 , противоречие. Следовательно
, противоречие. Следовательно 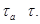 Значит,
Значит, 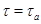 .
.
Теперь мы предположим, что решетка 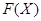 является цепью. Пусть
является цепью. Пусть  и
и 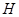 - конечная группа. Предположим, что порядок
- конечная группа. Предположим, что порядок 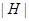 группы
группы 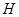 делится по крайней мере на два простых числа
делится по крайней мере на два простых числа  и
и 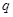 . Пусть
. Пусть 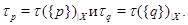
И пусть 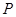 - силовская
- силовская  -подгруппа в
-подгруппа в 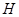 и
и 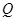 - силовская
- силовская 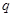 -подгруппа в
-подгруппа в 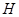 , соответственно. Тогда
, соответственно. Тогда 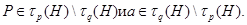
Значит, 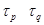 и
и 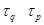 . Это показывает, что
. Это показывает, что 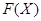 не является цепью, что противоречит нашему предположению. Следовательно, найдется такое простое число
не является цепью, что противоречит нашему предположению. Следовательно, найдется такое простое число  , что каждая конечная группа из
, что каждая конечная группа из 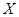 является
является  -группой.
-группой.
Мы теперь покажем, что каждая группа в 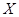 является абелевой. Предположим, что это не так и пусть
является абелевой. Предположим, что это не так и пусть 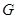 - неабелева группа в
- неабелева группа в 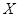 . В этом случае некоторая ее подгруппа
. В этом случае некоторая ее подгруппа 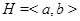 , порожденная элементами
, порожденная элементами 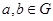 , является конечной неабелевой
, является конечной неабелевой  -группой. Так как по условию класс
-группой. Так как по условию класс 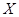 является наследственным, то
является наследственным, то  . Пусть
. Пусть 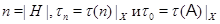 , где
, где 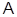 - класс всех абелевых групп. Поскольку
- класс всех абелевых групп. Поскольку 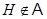 , то
, то 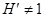 , и поэтому
, и поэтому  . Следовательно, мы имеем
. Следовательно, мы имеем 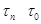 . Теперь пусть
. Теперь пусть 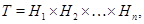 где
где 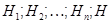 . И пусть
. И пусть 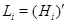 - коммутант подгруппы
- коммутант подгруппы 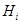 ,
, 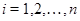 . Тогда
. Тогда 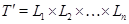 и ясно, что
и ясно, что 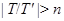 . Значит,
. Значит, 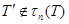 . Но поскольку
. Но поскольку 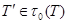 , мы имеем
, мы имеем 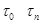 . Таким образом,
. Таким образом, 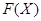 не является цепью. Полученное противоречие показывает, что каждая группа в
не является цепью. Полученное противоречие показывает, что каждая группа в 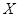 является абелевой. Аналогично можно показать, что экспонента каждой группы из
является абелевой. Аналогично можно показать, что экспонента каждой группы из 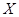 делит число
делит число 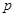 .
.
Теорема доказана.
Пересечение всех конечных многообразий, содержащих данную группу 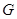 , называется конечным многообразием, порожденным
, называется конечным многообразием, порожденным 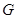 . Из теоремы 20.8 вытекает
. Из теоремы 20.8 вытекает
Теорема 20.9. Пусть 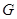 - конечная группа и
- конечная группа и 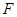 - конечное многообразие, порожденное
- конечное многообразие, порожденное 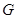 . Тогда в том и только в том случае
. Тогда в том и только в том случае 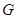 является элементарной абелевой
является элементарной абелевой  -группой, когда решетка
-группой, когда решетка 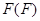 является цепью.
является цепью.
Пусть 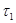 и
и 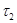 - подгрупповые
- подгрупповые 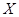 -функторы. Определим произведение
-функторы. Определим произведение 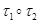 при помощи следующего правила
при помощи следующего правила 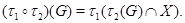
Понятно, что подгрупповой 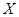 -функтор
-функтор 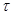 является замкнутым тогда и только тогда, когда
является замкнутым тогда и только тогда, когда 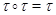 . Мы используем символ
. Мы используем символ 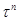 для обозначения произведения
для обозначения произведения 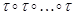 , в котором имеется
, в котором имеется 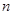 сомножителей.
сомножителей.
Пусть 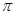 - произвольное непустое множество простых чисел. Подгруппа
- произвольное непустое множество простых чисел. Подгруппа 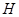 группы
группы 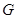 называется
называется 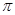 -холловской, если ее индекс
-холловской, если ее индекс 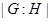 в
в 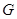 не делится ни на одно число из
не делится ни на одно число из 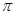 , а среди простых делителей ее порядка
, а среди простых делителей ее порядка 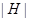 нет ни одного не входящего в
нет ни одного не входящего в 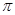 . Символом
. Символом 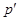 обозначают множество всех простых чисел, отличных от
обозначают множество всех простых чисел, отличных от 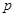 .
.
Конечная группа 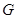 называется нильпотентной, если выполняется одно из эквивалентных условий:
называется нильпотентной, если выполняется одно из эквивалентных условий:
а) все силовские подгруппы нормальны в 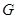 ;
;
б) все максимальные подгруппы (т.е. коатомы решетки 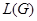 ) нормальны в
) нормальны в 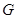 .
.
Лемма 24.9 Пусть 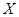 - наследственный гомоморф конечных групп. Пусть
- наследственный гомоморф конечных групп. Пусть 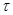 - замкнутый подгрупповой функтор на
- замкнутый подгрупповой функтор на 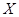 Пусть
Пусть 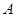 - нильпотентная группа в
- нильпотентная группа в 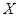 и
и 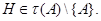 Предположим, что
Предположим, что 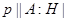 , где
, где  - простое число. Пусть
- простое число. Пусть 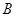 - нильпотентная группа в
- нильпотентная группа в 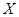 такая, что
такая, что 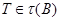 и
и 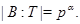 Тогда
Тогда 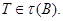
Доказательство. Пусть 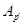 - холловская
- холловская  -подгруппа в
-подгруппа в 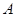 и
и 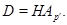 Предположим, что
Предположим, что 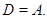 Тогда
Тогда 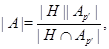
и поэтому 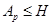 , где
, где 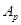 - силовская
- силовская  -подгруппа в
-подгруппа в 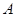 . Тогда
. Тогда 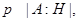 противоречие. Следовательно,
противоречие. Следовательно, 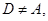 и поэтому найдется максимальная подгруппа
и поэтому найдется максимальная подгруппа 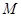 в
в 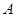 така1я, что
така1я, что 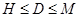 и
и 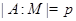 . Так как
. Так как 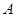 - нильпотентная группа, то
- нильпотентная группа, то 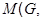 и поэтому согласно лемме 24.6, мы имеем
и поэтому согласно лемме 24.6, мы имеем 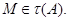 Теперь мы докажем, что
Теперь мы докажем, что 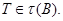 Если
Если 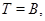 то по определению подгруппового функтора мы сразу имеем
то по определению подгруппового функтора мы сразу имеем 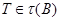 . Пусть
. Пусть 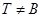 и пусть
и пусть 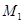 - максимальная подгруппа в
- максимальная подгруппа в 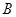 такая, что
такая, что 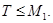 Тогда
Тогда 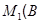 и так как
и так как 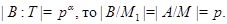
Так как 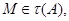 мы видим, что
мы видим, что 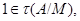 и поэтому
и поэтому 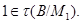 Следовательно,
Следовательно, 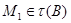 . Если
. Если 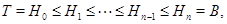 где
где 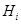 - максимальная подгруппа в
- максимальная подгруппа в 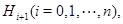 то
то 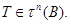 Но
Но 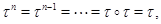 и поэтому мы видим, что
и поэтому мы видим, что 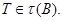 Лемма доказана.
Лемма доказана.
Лемма 24.10 Пусть 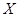 - наследственный гомоморф конечных нильпотентных групп и
- наследственный гомоморф конечных нильпотентных групп и 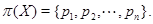 Пусть
Пусть 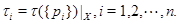 Если
Если 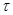 - идемпотент в
- идемпотент в 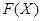 , удовлетворяющий условию
, удовлетворяющий условию 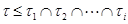 и
и 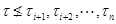 , где
, где 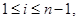 тогда
тогда 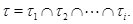
Доказательство. Предположим, что 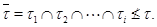 Тогда найдется группа
Тогда найдется группа 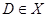 с
с 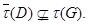 Мы можем предполагать, что
Мы можем предполагать, что 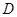 - группа минимального порядка с этим свойством. Следовательно,
- группа минимального порядка с этим свойством. Следовательно, 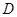 содержит подгруппу
содержит подгруппу 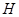 такую, что
такую, что 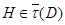 , но
, но 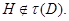 Ясно, что
Ясно, что 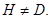 Пусть
Пусть 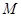 - максимальная подгруппа в
- максимальная подгруппа в 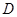 такая, что
такая, что 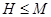 и пусть
и пусть  Так как
Так как 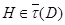 для каждого
для каждого 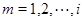 , мы имеем
, мы имеем 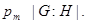 Понятно, что
Понятно, что 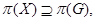 и поэтому
и поэтому 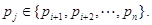 Так как группа
Так как группа 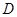 нильпотентна, то
нильпотентна, то  и поэтому по лемме 24.6,
и поэтому по лемме 24.6, 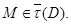 Так как
Так как 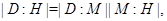 мы видим, что
мы видим, что 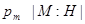 для всех
для всех 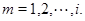 Следовательно,
Следовательно, 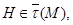 и поэтому по выбору группы
и поэтому по выбору группы 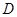 , мы имеем
, мы имеем 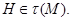 Так как по условию
Так как по условию 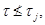 то найдется такая группа
то найдется такая группа 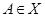 , что для некоторой ее подгруппы
, что для некоторой ее подгруппы 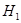 мы имеем
мы имеем 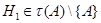 и
и 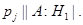 Используя теперь лемму 24.9, мы видим, что
Используя теперь лемму 24.9, мы видим, что 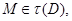 и поэтому
и поэтому 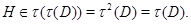
Полученное противоречие показывает, что 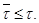 Но согласно нашему предположению, мы имеем
Но согласно нашему предположению, мы имеем 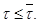 Следовательно,
Следовательно, 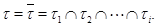
Пусть 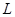 - решетка. Подмножество
- решетка. Подмножество 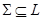 называется антицепью в
называется антицепью в 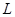 если для любых различных элементов
если для любых различных элементов 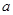 и
и 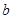 из
из 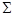 , мы имеем
, мы имеем 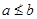 и
и 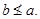 Если
Если 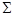 - антицепь в
- антицепь в 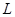 такая, что
такая, что 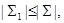 для любой другой антицепи
для любой другой антицепи 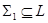 , тогда кардинальное число
, тогда кардинальное число 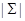 называется шириной решетки
называется шириной решетки 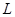 .
.
Если 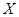 - произвольная совокупность групп, то символом
- произвольная совокупность групп, то символом 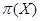 обозначается множество всех простых делителей порядков групп из
обозначается множество всех простых делителей порядков групп из 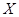 .
.
Теорема 24.11 Пусть 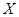 - конечное многообразие групп. И пусть каждая группа в
- конечное многообразие групп. И пусть каждая группа в 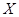 конечная. Тогда ширина
конечная. Тогда ширина 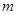 решетки
решетки 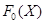 всех идемпотентов в
всех идемпотентов в 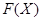 конечна и
конечна и  в том и только в том случае, когда
в том и только в том случае, когда 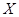 состоит из нильпотентных групп и
состоит из нильпотентных групп и 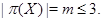
Доказательство. Прежде мы предположим, что формация 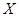 нильпотентна и
нильпотентна и 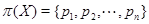 , где
, где 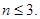 Пусть
Пусть 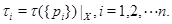 Предположим, что имеется замкнытый функтор
Предположим, что имеется замкнытый функтор 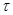 в
в 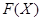 такой, что
такой, что 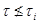 и
и 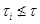 для
для 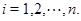 Мы покажем, что
Мы покажем, что 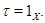 Действительно, если
Действительно, если 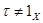 , тогда найдется группа
, тогда найдется группа 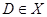 такая, что для некоторой подгруппы
такая, что для некоторой подгруппы 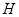 из
из 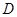 , мы имеем
, мы имеем 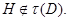 Мы можем считать, что
Мы можем считать, что 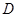 - группа минимального порядка с этим свойством. Понятно, что
- группа минимального порядка с этим свойством. Понятно, что 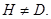 Пусть
Пусть 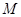 - такая максимальная подгруппа в
- такая максимальная подгруппа в 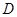 , что
, что 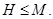 . Согласно условию, класс
. Согласно условию, класс 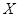 является наследственным. Следовательно,
является наследственным. Следовательно, 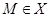 , и поэтому ввиду выбора группы
, и поэтому ввиду выбора группы 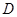 , мы имеем
, мы имеем 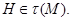 Пусть
Пусть 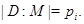 Так как
Так как 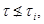 то найдется группа
то найдется группа 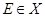 такая, что
такая, что 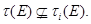 Таким образом, для некоторой подгруппы
Таким образом, для некоторой подгруппы 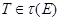 мы имеем
мы имеем 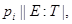 и поэтому по лемме 4.9,
и поэтому по лемме 4.9, 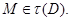 Это означает, что
Это означает, что 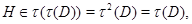 противоречие. Следовательно,
противоречие. Следовательно, 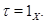 Значит, если
Значит, если 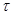 - замкнутый функтор в
- замкнутый функтор в 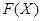 и
и 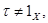 то для некоторого
то для некоторого 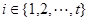 мы имеем
мы имеем 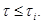 По лемме мы видим, что ширина
По лемме мы видим, что ширина 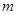 решетки
решетки 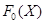 равна
равна 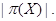
Теперь мы предположим, что ширина 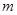 решетки
решетки 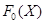 конечна и
конечна и 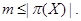 Пусть
Пусть 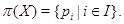 Если
Если 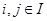 и
и 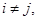 тогда
тогда 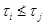 и
и 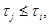 и поэтому
и поэтому 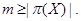 Это означает, что
Это означает, что 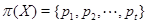 - конечное множество. Теперь мы покажем, что
- конечное множество. Теперь мы покажем, что 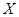 - класс нильпотентных групп. Предположим, что
- класс нильпотентных групп. Предположим, что 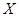 имеет ненильпотентную
имеет ненильпотентную 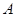 . Пусть
. Пусть 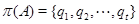 и пусть
и пусть 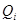 - силовская
- силовская 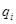 -подгруппа в
-подгруппа в 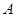 . Тогда
. Тогда 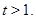 Так как
Так как 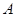 - ненильпотентная группа, то для некоторого
- ненильпотентная группа, то для некоторого 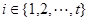 имеет место
имеет место 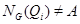 . Хорошо известно (см., например, [], теорема), что
. Хорошо известно (см., например, [], теорема), что 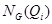 не является субнормальной подгруппой в
не является субнормальной подгруппой в 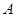 , и поэтому
, и поэтому 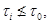 где
где 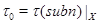 (см. пример 21.4). С другой стороны, мы видим, что
(см. пример 21.4). С другой стороны, мы видим, что 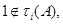 и поэтому
и поэтому 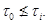 Это показывает, что
Это показывает, что 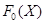 антицепь
антицепь 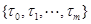 с
с 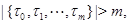 противоречие. Таким образом,
противоречие. Таким образом, 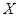 - формация, состоящая из нильпотентных групп. А по лемме 4.10,
- формация, состоящая из нильпотентных групп. А по лемме 4.10, 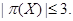 Теорема доказана.
Теорема доказана.
Заключение
Отметим, что теория подгрупповых функторов уже нашла много примениний при иследовании внутреннего строения конечных групп [1, 2, 3, 4]. Но еще один аспект применения подгупповых функторов состоит в сопоставлении группе некоторой решетки подгупповых функторов свойства которой тесно связаны со свойствами самой группы. Это позволяет использовать строение группы в зависимости от условий налогаемых на соответствующую решетку подгупповых функторов.
Следует отметить также, что используя понятие подгуппового функтора можно строить новые типы решеток, что указывает на полезность этого понятия и для теории решеток.



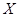 решетки
решетки 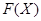 и
и 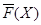 можно изучать свойства групп из
можно изучать свойства групп из 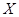 в зависимости от свойств решеток
в зависимости от свойств решеток 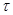 - подгрупповой функтор и
- подгрупповой функтор и 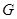 - группа. Если
- группа. Если 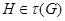 и
и  , тогда
, тогда 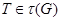 .
.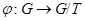 - канонический эпиморфизм
- канонический эпиморфизм 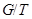 , то
, то 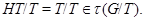
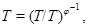 мы видим по определению подгрупповых функторов, что
мы видим по определению подгрупповых функторов, что 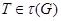 .
.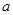 - элемент группы
- элемент группы 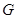 . Тогда если для некоторого натурального числа
. Тогда если для некоторого натурального числа 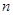 имеет место
имеет место 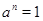 , то наименьшее натуральное число
, то наименьшее натуральное число 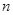 с таким свойством называется порядком элемента
с таким свойством называется порядком элемента 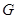 - группа экспоненты
- группа экспоненты 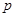 , если каждый ее неединичный элемент имеет порядок
, если каждый ее неединичный элемент имеет порядок 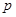 .
.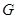 - абелева группа экспоненты
- абелева группа экспоненты  .
.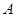 ,
, 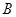 - элементарно абелевы
- элементарно абелевы 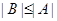 . Тогда
. Тогда 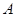 имеет подгруппу
имеет подгруппу  такую, что
такую, что 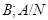 .
.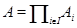 и
и 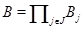 , где
, где 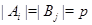 для всех
для всех 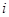 и
и 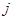 . Пусть
. Пусть 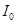 - подмножество в
- подмножество в 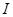 такое, что
такое, что 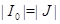 . И пусть
. И пусть 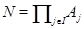 , где
, где 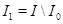 и
и 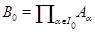 . Тогда ясно, что
. Тогда ясно, что 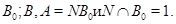
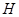 группы
группы 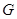 называется силовской
называется силовской 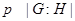 и
и 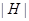 - степень числа
- степень числа 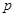 . Известная в теории групп теорема Силова утверждает, что для любого простого числа
. Известная в теории групп теорема Силова утверждает, что для любого простого числа 
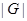 имеется силовская
имеется силовская 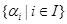 - такой набор конгруэнций
- такой набор конгруэнций  -алгебры A, что
-алгебры A, что 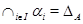 . Пусть
. Пусть 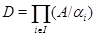 прямое произведение факторалгебр
прямое произведение факторалгебр 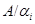 и
и 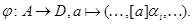
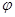 - мономорфизм алгебры
- мономорфизм алгебры 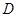 и
и 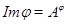 входит подпрямо в
входит подпрямо в 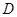 ., класс
., класс 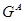 пишут
пишут 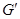 . Подгруппа
. Подгруппа 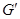 называется коммутантом группы
называется коммутантом группы 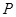 - конечная
- конечная 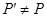 . Легко проверить, что если
. Легко проверить, что если 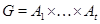 , то
, то 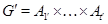
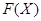 является цепью, когда существует такое простое число
является цепью, когда существует такое простое число 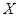 является элементарно абелевой
является элементарно абелевой 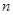 , мы полагаем
, мы полагаем 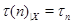 (см. пример 20.2). Понятно, что
(см. пример 20.2). Понятно, что 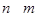 влечет, что
влечет, что 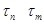 . Для доказательства того, что
. Для доказательства того, что 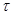 со свойством
со свойством 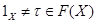 найдется кардинальное число
найдется кардинальное число 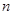 такое, что
такое, что 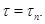
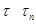 для всех кардинальных чисел
для всех кардинальных чисел 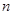 . Тогда
. Тогда 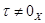 . Поскольку
. Поскольку 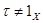 , то найдется группа
, то найдется группа 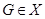 такая, что для некоторой ее подгруппы
такая, что для некоторой ее подгруппы 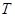 мы имеем
мы имеем 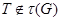 . Пусть
. Пусть 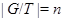 . Поскольку
. Поскольку 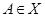 такая, что для некоторой ее подгруппы
такая, что для некоторой ее подгруппы 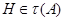 мы имеем
мы имеем 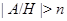 . По лемме 20.6, мы видим, что для всех подгрупп
. По лемме 20.6, мы видим, что для всех подгрупп 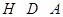 , мы имеем
, мы имеем 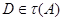 . Следовательно,
. Следовательно, 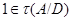 . Используя лемму 20.7, мы видим, что имеется подгруппа
. Используя лемму 20.7, мы видим, что имеется подгруппа 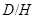 в группе
в группе 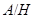 такая, что
такая, что 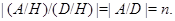
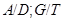 , и поэтому
, и поэтому 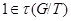 . Если
. Если 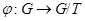 - канонический эпиморфизм, который отображает
- канонический эпиморфизм, который отображает 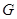 на
на 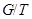 , то
, то 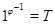 , и поэтому
, и поэтому 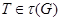 . Это противоречие показывает, что для некоторого кардинального числа
. Это противоречие показывает, что для некоторого кардинального числа 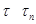 .
.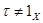 и так как каждая группа в
и так как каждая группа в 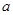 - наименьшее натуральное число такое, что
- наименьшее натуральное число такое, что 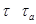 . Мы покажем, что
. Мы покажем, что 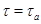 . Предположим, что
. Предположим, что 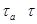 и пусть
и пусть 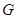 - группа из
- группа из 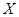 такая, что
такая, что 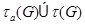 . В этом случае пусть
. В этом случае пусть 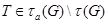 . Тогда
. Тогда 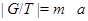 . Теперь, по выбору числа
. Теперь, по выбору числа 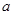 , мы имеем
, мы имеем 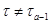 . Это означает, что найдется группа
. Это означает, что найдется группа 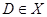 такая, что
такая, что 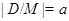 для некоторой подгруппы
для некоторой подгруппы 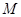 из
из 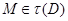 . Пусть
. Пусть 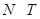 и
и 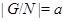 . Тогда
. Тогда 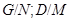 . Так как
. Так как 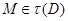 , мы имеем
, мы имеем 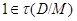 , и поэтому
, и поэтому 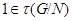 . Но тогда
. Но тогда 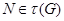 , и поэтому
, и поэтому 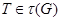 , противоречие. Следовательно
, противоречие. Следовательно 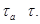 Значит,
Значит,  и
и 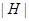 группы
группы 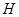 делится по крайней мере на два простых числа
делится по крайней мере на два простых числа 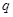 . Пусть
. Пусть 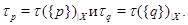
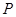 - силовская
- силовская  и
и 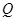 - силовская
- силовская 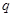 -подгруппа в
-подгруппа в 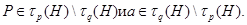
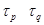 и
и 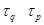 . Это показывает, что
. Это показывает, что 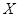 . В этом случае некоторая ее подгруппа
. В этом случае некоторая ее подгруппа 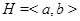 , порожденная элементами
, порожденная элементами 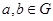 , является конечной неабелевой
, является конечной неабелевой 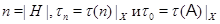 , где
, где 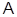 - класс всех абелевых групп. Поскольку
- класс всех абелевых групп. Поскольку 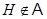 , то
, то 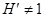 , и поэтому
, и поэтому  . Следовательно, мы имеем
. Следовательно, мы имеем 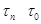 . Теперь пусть
. Теперь пусть 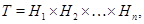 где
где 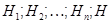 . И пусть
. И пусть 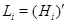 - коммутант подгруппы
- коммутант подгруппы 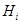 ,
, 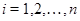 . Тогда
. Тогда 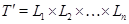 и ясно, что
и ясно, что 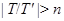 . Значит,
. Значит, 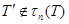 . Но поскольку
. Но поскольку 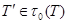 , мы имеем
, мы имеем 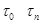 . Таким образом,
. Таким образом, 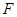 - конечное многообразие, порожденное
- конечное многообразие, порожденное 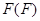 является цепью.
является цепью.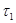 и
и 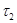 - подгрупповые
- подгрупповые 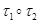 при помощи следующего правила
при помощи следующего правила 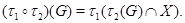
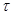 является замкнутым тогда и только тогда, когда
является замкнутым тогда и только тогда, когда 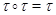 . Мы используем символ
. Мы используем символ 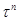 для обозначения произведения
для обозначения произведения 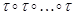 , в котором имеется
, в котором имеется 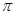 - произвольное непустое множество простых чисел. Подгруппа
- произвольное непустое множество простых чисел. Подгруппа 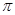 -холловской, если ее индекс
-холловской, если ее индекс 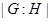 в
в 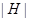 нет ни одного не входящего в
нет ни одного не входящего в 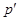 обозначают множество всех простых чисел, отличных от
обозначают множество всех простых чисел, отличных от 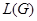 ) нормальны в
) нормальны в 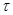 - замкнутый подгрупповой функтор на
- замкнутый подгрупповой функтор на 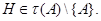 Предположим, что
Предположим, что 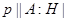 , где
, где 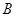 - нильпотентная группа в
- нильпотентная группа в 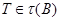 и
и 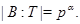 Тогда
Тогда 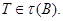
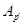 - холловская
- холловская 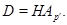 Предположим, что
Предположим, что 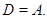 Тогда
Тогда 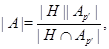
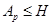 , где
, где 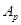 - силовская
- силовская 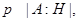 противоречие. Следовательно,
противоречие. Следовательно, 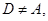 и поэтому найдется максимальная подгруппа
и поэтому найдется максимальная подгруппа 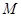 в
в 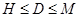 и
и 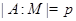 . Так как
. Так как 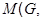 и поэтому согласно лемме 24.6, мы имеем
и поэтому согласно лемме 24.6, мы имеем 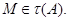 Теперь мы докажем, что
Теперь мы докажем, что 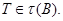 Если
Если 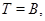 то по определению подгруппового функтора мы сразу имеем
то по определению подгруппового функтора мы сразу имеем 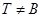 и пусть
и пусть 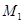 - максимальная подгруппа в
- максимальная подгруппа в 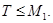 Тогда
Тогда 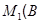 и так как
и так как 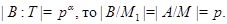
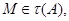 мы видим, что
мы видим, что 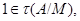 и поэтому
и поэтому 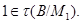 Следовательно,
Следовательно, 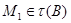 . Если
. Если 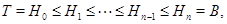 где
где 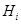 - максимальная подгруппа в
- максимальная подгруппа в 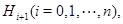 то
то 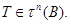 Но
Но 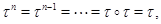 и поэтому мы видим, что
и поэтому мы видим, что 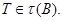 Лемма доказана.
Лемма доказана.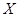 - наследственный гомоморф конечных нильпотентных групп и
- наследственный гомоморф конечных нильпотентных групп и 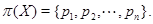 Пусть
Пусть 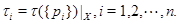 Если
Если 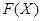 , удовлетворяющий условию
, удовлетворяющий условию 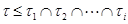 и
и 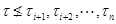 , где
, где 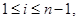 тогда
тогда 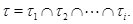
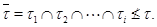 Тогда найдется группа
Тогда найдется группа 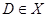 с
с 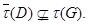 Мы можем предполагать, что
Мы можем предполагать, что 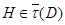 , но
, но 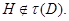 Ясно, что
Ясно, что 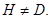 Пусть
Пусть 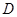 такая, что
такая, что 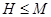 и пусть
и пусть  Так как
Так как 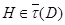 для каждого
для каждого 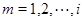 , мы имеем
, мы имеем 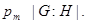 Понятно, что
Понятно, что 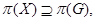 и поэтому
и поэтому 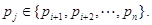 Так как группа
Так как группа 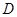 нильпотентна, то
нильпотентна, то  и поэтому по лемме 24.6,
и поэтому по лемме 24.6, 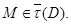 Так как
Так как 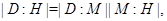 мы видим, что
мы видим, что 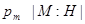 для всех
для всех 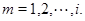 Следовательно,
Следовательно, 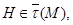 и поэтому по выбору группы
и поэтому по выбору группы 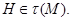 Так как по условию
Так как по условию 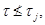 то найдется такая группа
то найдется такая группа 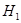 мы имеем
мы имеем 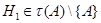 и
и 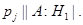 Используя теперь лемму 24.9, мы видим, что
Используя теперь лемму 24.9, мы видим, что 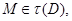 и поэтому
и поэтому 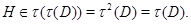
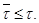 Но согласно нашему предположению, мы имеем
Но согласно нашему предположению, мы имеем 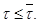 Следовательно,
Следовательно, 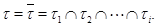
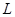 - решетка. Подмножество
- решетка. Подмножество 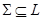 называется антицепью в
называется антицепью в 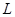 если для любых различных элементов
если для любых различных элементов 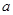 и
и 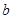 из
из 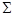 , мы имеем
, мы имеем 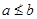 и
и 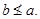 Если
Если 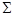 - антицепь в
- антицепь в 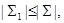 для любой другой антицепи
для любой другой антицепи 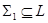 , тогда кардинальное число
, тогда кардинальное число 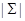 называется шириной решетки
называется шириной решетки 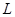 .
.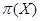 обозначается множество всех простых делителей порядков групп из
обозначается множество всех простых делителей порядков групп из 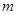 решетки
решетки 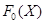 всех идемпотентов в
всех идемпотентов в 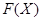 конечна и
конечна и  в том и только в том случае, когда
в том и только в том случае, когда 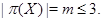
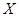 нильпотентна и
нильпотентна и 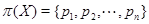 , где
, где 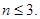 Пусть
Пусть 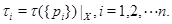 Предположим, что имеется замкнытый функтор
Предположим, что имеется замкнытый функтор 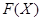 такой, что
такой, что 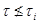 и
и 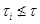 для
для 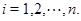 Мы покажем, что
Мы покажем, что 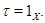 Действительно, если
Действительно, если 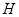 из
из 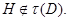 Мы можем считать, что
Мы можем считать, что 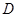 - группа минимального порядка с этим свойством. Понятно, что
- группа минимального порядка с этим свойством. Понятно, что 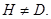 Пусть
Пусть 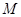 - такая максимальная подгруппа в
- такая максимальная подгруппа в 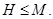 . Согласно условию, класс
. Согласно условию, класс 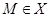 , и поэтому ввиду выбора группы
, и поэтому ввиду выбора группы 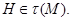 Пусть
Пусть 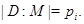 Так как
Так как 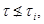 то найдется группа
то найдется группа 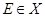 такая, что
такая, что 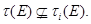 Таким образом, для некоторой подгруппы
Таким образом, для некоторой подгруппы 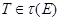 мы имеем
мы имеем 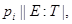 и поэтому по лемме 4.9,
и поэтому по лемме 4.9, 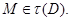 Это означает, что
Это означает, что 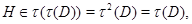 противоречие. Следовательно,
противоречие. Следовательно, 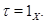 Значит, если
Значит, если 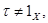 то для некоторого
то для некоторого 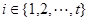 мы имеем
мы имеем 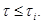 По лемме мы видим, что ширина
По лемме мы видим, что ширина 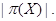
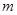 решетки
решетки 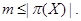 Пусть
Пусть 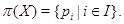 Если
Если 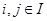 и
и 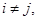 тогда
тогда 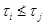 и
и 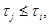 и поэтому
и поэтому 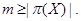 Это означает, что
Это означает, что 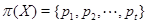 - конечное множество. Теперь мы покажем, что
- конечное множество. Теперь мы покажем, что 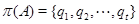 и пусть
и пусть 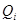 - силовская
- силовская 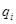 -подгруппа в
-подгруппа в 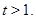 Так как
Так как 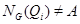 . Хорошо известно (см., например, [], теорема), что
. Хорошо известно (см., например, [], теорема), что 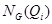 не является субнормальной подгруппой в
не является субнормальной подгруппой в 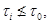 где
где 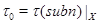 (см. пример 21.4). С другой стороны, мы видим, что
(см. пример 21.4). С другой стороны, мы видим, что 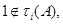 и поэтому
и поэтому 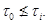 Это показывает, что
Это показывает, что 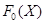 антицепь
антицепь 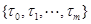 с
с 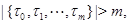 противоречие. Таким образом,
противоречие. Таким образом, 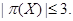 Теорема доказана.
Теорема доказана.