Пусть функция f (x) непрерывна и положительна на [ a; b ]. Рассмотрим криволинейную трапецию ABCD, интегральная сумма

дает сумму площадей прямоугольников с основаниями  . Ее можно принять за приближенное значение площади криволинейной трапеции ABCD, т.е.
. Ее можно принять за приближенное значение площади криволинейной трапеции ABCD, т.е.

Данное равенство будет тем точнее, чем мельче дробление, и в пределе при 

В этом и заключается геометрический смысл определенного интеграла.
1.4. Свойства определенного интеграла
1. Постоянный множитель выносим за знак интеграла, т.е. если c – некоторое число, то

Доказательство:


2. Определенный интеграл от суммы нескольких функций равен сумме определенных интегралов от слагаемых

Доказательство:



3. Для любых трех чисел a, b, c справедливо следующее равенство

если все эти интегралы существуют.
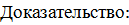
 составим интегральную сумму так, чтобы точка с была точкой деления, тогда:
составим интегральную сумму так, чтобы точка с была точкой деления, тогда:

Переходя к пределу при  получили доказательство.
получили доказательство.
Если a<b<c, то, по только что доказанному получим:

Или
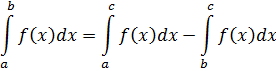


4. Если на [ a; b ] (a < b) f (x)≤ g (x), то





Следствия:
1. Если a < b и 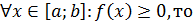

2. Если a<b 

3. Теорема об оценке определенного интеграла
Если m и M – наименьшее и наибольшее значения функции f (x) на [ a; b ], a < b, то
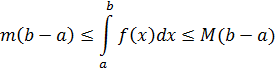
Доказательство:
т.к. 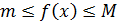 , то по 4 свойству
, то по 4 свойству

отсюда мы знаем, что

Следовательно:
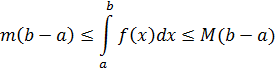
4. Теорема о среднем
Если функция f(x) непрерывна на [a;b], то на этом отрезке найдется такая точка 

Доказательство:
Пусть a<b, m и M – наименьшее и наибольшее значения функции f (x) на [a;b]. По свойству 5 получаем:


Тогда

Так как функция f (x) Непрерывна на [a;b], она принимает на нем все промежуточные значения между m и M, то есть существует 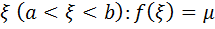 . Тогда:
. Тогда:

Глава 2. Вычисление определенного интеграла
Теорема об интеграле с переменным верхним пределом
(теорема Барроу)
Теорема.
Если функция f(x) непрерывна на [a;b], то интеграл с переменным верхним пределом

имеет производную, равную значению подынтегральной функции при верхнем пределе, т.е.

Доказательство.
Пусть  - приращение аргумента x. тогда по свойству 3 определенного интеграла
- приращение аргумента x. тогда по свойству 3 определенного интеграла


По теореме о среднем (свойство 6)  , при чем
, при чем 

При  и по непрерывности функции
и по непрерывности функции 

Таким образом, 
Замечание.
Из теоремы следует, что определенный интеграл с переменным верхним пределом  является первообразной для подынтегральной функции f(x) на отрезке [a;b]:
является первообразной для подынтегральной функции f(x) на отрезке [a;b]:

То есть, установлена связь между неопределенным и определенным интегралами.
Формула Ньютона-Лейбница
В предыдущем пункте показано, что функция f(x), непрерывная на отрезке [a;b], имеет первообразную. В качестве первообразной можно взять следующую функцию

то есть интеграл с переменным верхним пределом.
Теперь поставим обратную задачу, то есть зная одну из первообразных Ф(х) функции f (x) на [ a; b ], вычислить определенный интеграл от f(x) на этом отрезке или найти определенный интеграл по известному неопределенному.
Следующая теорема показывает основную формулу интегрального исчисления, то есть формулу Ньютона-Лейбница (выражает определенный интеграл, через неопределенный).
Теорема.
Если F (x) является первообразной непрерывной функции f (x), то справедлива формула:

Доказательство.
По теореме Барроу  - первообразная функции f (x), поэтому F (x) и
- первообразная функции f (x), поэтому F (x) и  отличаются на константу C, то есть
отличаются на константу C, то есть

Пусть x = a, тогда 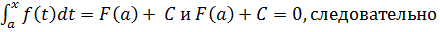
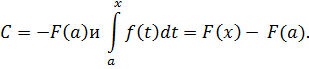
Но приняв в этом равенстве x = b, получается формула Ньютона – Лейбница:

Символ  называется двойной подстановкой в функцию F(x) в пределах от a до b, таким образом формулу:
называется двойной подстановкой в функцию F(x) в пределах от a до b, таким образом формулу:

Можно записать в виде:

Пример 1.

Пример 2.
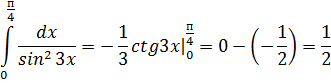
Пример 3.
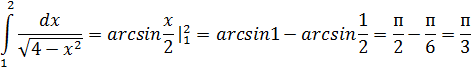
Замена переменных
Теорема.
Рассмотрим

где f (x) непрерывна на [a,b]. Введем новую функцию 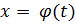 , заданную на
, заданную на  и удовлетворяющую следующим условиям:
и удовлетворяющую следующим условиям:
1.  непрерывны на
непрерывны на  ;
;
2. может быть определена сложная функция  ;
;
3.  .
.
Тогда:

Доказательство.
Для проверки можно заметить, что если F(x) является первообразной для f(x), то очевидно 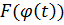 - первообразная для подынтегральной функции в правой части полученной формулы, значит:
- первообразная для подынтегральной функции в правой части полученной формулы, значит:
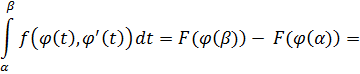

Пример 1.

Сделаем замену  . Найдем
. Найдем 
 и вычислим новые пределы интегрирования
и вычислим новые пределы интегрирования  Тогда:
Тогда:

Пример 2.

Сделаем замену  . Вычислим новые пределы интегрирования
. Вычислим новые пределы интегрирования  Тогда:
Тогда:
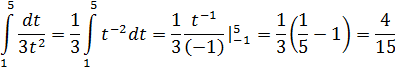
Интегрирование по частям
Теорема.
Пусть функции u(x) и v(x) дифференцируемы на отрезке [a;b], то справедлива следующая формула:

Или в компактной форме можно записать:

Эта формула называется формулой интегрирования по частям для определенного интеграла.
Доказательство.
Применим формулу Ньютона – Лейбница и формулу интегрирования по частям в неопределенном интеграле:


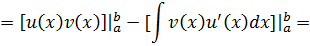

Теорема доказана.
Пример 1.Вычислить:

Решение: пусть  , тогда
, тогда  . По формуле интегрирования по частям:
. По формуле интегрирования по частям:
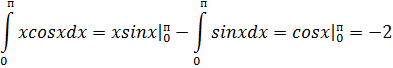
Пример 2. Найти:
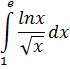
Решение:  , тогда
, тогда  , и по формуле интегрирования по частям:
, и по формуле интегрирования по частям:






 . Ее можно принять за приближенное значение площади криволинейной трапеции ABCD, т.е.
. Ее можно принять за приближенное значение площади криволинейной трапеции ABCD, т.е.










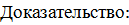
 составим интегральную сумму так, чтобы точка с была точкой деления, тогда:
составим интегральную сумму так, чтобы точка с была точкой деления, тогда:
 получили доказательство.
получили доказательство.
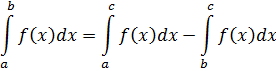







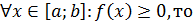



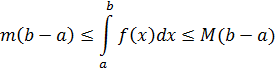
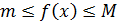 , то по 4 свойству
, то по 4 свойству






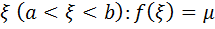 . Тогда:
. Тогда:


 - приращение аргумента x. тогда по свойству 3 определенного интеграла
- приращение аргумента x. тогда по свойству 3 определенного интеграла

 , при чем
, при чем 

 и по непрерывности функции
и по непрерывности функции 


 является первообразной для подынтегральной функции f(x) на отрезке [a;b]:
является первообразной для подынтегральной функции f(x) на отрезке [a;b]:


 - первообразная функции f (x), поэтому F (x) и
- первообразная функции f (x), поэтому F (x) и 
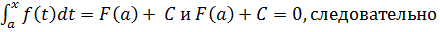
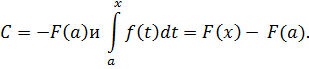

 называется двойной подстановкой в функцию F(x) в пределах от a до b, таким образом формулу:
называется двойной подстановкой в функцию F(x) в пределах от a до b, таким образом формулу:

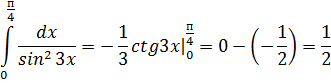
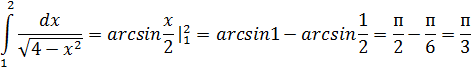

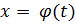 , заданную на
, заданную на  и удовлетворяющую следующим условиям:
и удовлетворяющую следующим условиям: непрерывны на
непрерывны на  ;
; .
.
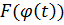 - первообразная для подынтегральной функции в правой части полученной формулы, значит:
- первообразная для подынтегральной функции в правой части полученной формулы, значит: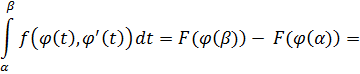


 . Найдем
. Найдем 
 и вычислим новые пределы интегрирования
и вычислим новые пределы интегрирования  Тогда:
Тогда:

 . Вычислим новые пределы интегрирования
. Вычислим новые пределы интегрирования  Тогда:
Тогда: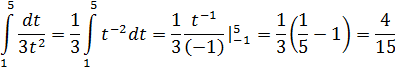




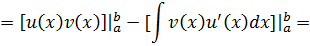


 , тогда
, тогда  . По формуле интегрирования по частям:
. По формуле интегрирования по частям: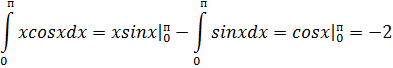
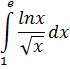
 , тогда
, тогда  , и по формуле интегрирования по частям:
, и по формуле интегрирования по частям:




