Цели олимпиад по программированию:
· выявить на ранней стадии одаренных детей для того, чтобы можно было продолжать работу с ними в дальнейшем в ВУЗах;
· для школьников же наличие элемента соревновательности, стимулирует их дальнейший интерес в области программирования и самоутверждения.
При проведении олимпиады по программированию нужно выявить три фактора у участника олимпиады:
1. умение квалифицированной работы на компьютере,
2. усвоение технологии программирования,
3. уровень алгоритмического мышления.
Технология программирования содержит следующие этапы:
1. Определение технического задания,
2. Алгоритмизация,
3. Выбор языка программирования,
4. Выбор структуры данных,
5. Описание алгоритма,
6. Оптимизация (глобальная, локальная, техническая),
7. Подготовка отладки,
8. Подготовка тестов,
9. Программирование,
10. Тестирование и отладка,
11. Документирование.
При определении уровня освоения технологии программирования появляется необходимость выделения двух туров:
1) теоретического тура, который может содержать 2,3,4,5,9 и 10 этапы технологии программирования,
2) практический тур на ЭВМ, который может содержать со 2-го по 11 этапы.
На олимпиаде можно проверить следующие способности:
· разработка эффективного алгоритма;
· методы программирования конкретного алгоритма на языке программирования;
· программирование данного алгоритма;
· отладка программы;
· тестирование программы;
· модификация существующей программы.
Поскольку в олимпиаде должен присутствовать элемент соревновательности, то надо вносить меру для оценки решенной задачи участником олимпиады, что позволит произвести ранжировку участников.
Предварительно оценим технические возможности ученика при написании и отладке 4-5 программ на олимпиаде. Квалифицированная машинистка при наборе текста в течении рабочего дня набирает около 25 страниц текста. За полдня около 12. Таким образом, в среднем объем текста, одной решенной задачи, не более 2 страниц.
Олимпиадная задача для ученика состоит из трех компонент:
1. Условие задачи (легенда), которое для восприятия обычно по объему не превышает 1/3 страницы. По структуре для улучшения контроля результата решения определяется формат входных и выходных данных и для уточнения условия задачи предлагаются примеры по условию задачи с ожидаемыми правильными ответами,
2. решение задачи, которое, исходя из возможности записи текста ученика, не должна превышать 2-х страниц,
3. ответ, полученный в результате работы программы участника олимпиады.
При работе жюри на олимпиаде если участвует свыше 70 учеников и они пишут текст около 8 страниц, то набирается свыше 500 страниц текста. Если все члены жюри будут просматривать при проверке все работы, то необходимо только прочтение работ одним человеком займет несколько дней. Поэтому эту работу необходимо разделить по членам жюри, Возможны различные способы разделения:
— Раздача работ по членам жюри. Этот метод не позволяет обеспечить определение единой шкалы при оценке работ. Результат будет зависить от того, к кому попадет конкретная работа. Соответственно, сможет ли он адекватно определить правильность работы и дать ей объективную оценку,
— Разбиение членов жюри по задачам, что позволяет обеспечить единый подход в оценке решения конкретной задачи и более адекватном определении правильности программ. Хотя остается проблема относительной объективности оценок.
В данном случае наиболее приемлем второй подход. При этом подходе обеспечивается сокращение проверяемого текста решения задач до 120-150 страниц.
Этот подход при внимательном изучении работ и оценке результата требует также много времени.
Так, для облегчения процесса проверки работы можно предложить выделение наиболее вероятного множества призеров через проверку правильности ответа. Если ученик во всех решаемых задачах формулирует неправильные ответы, то его можно исключать из множества возможных призеров и дать оценку по работе по наличию фрагментов наиболее вероятного варианта правильного решения не более половины допустимого числа баллов по данной задаче или не более половины минимального балла среди предложенных по всем задачам.
При этом подходе преимущество получают участники, решившие наибольшее число задач. Но из поля зрения выпадают остальные участники, которые возможно имеют оригинальные решения.
Для того, чтобы этот метод сработал более эффективно, необходимо разноплановость решаемых задач, чтобы каждая задача была трудной для большей части участников и разных групп участников. Тогда число наиболее вероятных претендентов будет около 1/10 или наиболее внимательно надо будет анализировать около 15-20 страниц текста решения задач, что уже более реально.
Для облегчения контроля ответов введем понятие F-простой задачи в данной теории Т.
Определение: Пусть задана теория Т. Задача Z называется F-простой задачей в теории Т, если длина записи условия задачи Z -короткая и ответ задачи имеет короткую длину записи.
Набор олимпиадных задач по математике или по физике имеет обычно свойство F-простоты.
Это свойство F-простоты олимпиадных задач позволяет членам жюри легко отсекать участников олимпиады, не решивших задачу, по полученному ответу. Основное внимание уделяется только небольшой группе участников олимпиады, у которых имеются правильные ответы, и только среди них удается более четко провести ранжирование участников по местам. Остальная же группа участников олимпиады очень грубо оценивается и полученое ранжирование плохо отражает реальную расстановку мест в середине таблицы. При оценке методов решения в основном учитывается только наличие метода решения и многие технические погрешности игнорируются.
В задачах по программированию по сравнению с задачами по математике или по физике как результат решения рассматривается метод решения задачи. Естественно для каждой задачи существует большое многообразие методов решения задач и те традиционные методы подбора задач, которые могут использоваться в математических или физических олимпиадах не приемлемы для олимпиад по программированию, поскольку члены жюри не смогут квалифицированно ранжировать участников олимпиады.
При оценке решения задач по программированию важную роль играют два фактора:
— правильноcть решения данной программой поставленной задачи;
— метод решения задачи.
При наличии большого парка компьютеров эта проблема может решаться традиционными методами. Т.е. в начале можно проверить правильность программы тестированием, которые могут отсечь большую группу участников, но затем можно рассматривать у остальных примененные методы решения. Затем как в математической олимпиаде провести ранжирование мест. На олимпиадах, где большое число участников, оценка результатов производится по пройденным тестам, хотя из-за некоторой несобранности участника олимпиады определивший правильный алгоритм может оказаться с нулевым числом баллов, а участник, рассмотревший только очевидные частные случаи получить высокие результаты.
Эта специфика осложняет процесс оценки задачи поэтому появляется необходимость определения принципа подбора задач, которая специфична для олимпиад по программированию.
Для данных олимпиад можно предложить решение F-простой задачи, чтобы участник олимпиады мог определить исходное условие данной задачи. В такой постановке задача остается F-простой.
Организаторы современных олимпиад, начиная с городского уровня, стараются, используя задачи из класса F-простых, автоматизировать проверку работ участников олимпиад. Процесс проверки и оценки предъявленных работ сводится к сумме баллов полученным по пройденным тестам. И работа жюри сводится к разработке системы тестов и их ценности.
При подборе задач для олимпиад по программированию нужен такой набор задач, который позволил бы охватить основной класс задач и позволил бы легко организовать проверку. Т.е. многообразие решений, которых было бы ограниченно и их решения были бы “прозрачны”.
Данный подход имеет два недостатка:
1) Система тестов может оказаться неполной и неправильная программа может быть оценена выше более правильной, которая имеет некоторые погрешности в учтенных ветвях решения, или не получила дополнительных баллов в неучтенных ветвях;
2) Поскольку при данной системе оценки работы не рассматривается метод решения, соответственно, оригинальность решения задачи остается за пределами поля зрения жюри.
Для использования в олимпиадах с данными требованиями к работе жюри наиболее подходящими и многократно опробованными являются следующие классы задач:
—определение задачи, решаемой заданной программой;
—задачи на сортировки с учетом различных особенностей заданной последовательности или сложностных характеристик;
—задачи – фильтры, которые позволяют организовать быстрое тестирование правильности программы;
—алгоритмические задачи, которые не имеют аналитического решения но решаются алгоритмически;
и т.п.
Примеры олимпиадных задач
Определение алгоритма
Например, рассмотрим следующий пример:
Для построения на алфавитно-цифровом дисплее прямой линии написана следующая программа:
For X:=X1 to X2 do
Begin
Y:=Y1+(Y2-Y1)*(X-X1)/(X2-X1)
Gotoxy(x,y);
Write(‘█’)
End;
Y=[Y1+(Y2-Y1)*(X-X1)/(X2-X1)]
Эта прямая (X1,Y1,X2,Y2) представляется такой ступенчатой функцией. Но если соотношение между координатами —
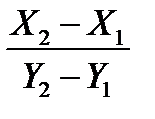 < 1, то у этой прямой получится следующий вид
< 1, то у этой прямой получится следующий вид
 т.е. проводник размыкается из-за того, что между ступенями расстояние больше 1.
т.е. проводник размыкается из-за того, что между ступенями расстояние больше 1.
При построении прямой такого вида нужно строить вертикальные линии следующего вида
Здесь строится прямая при фиксированном X:
от Y=[Y1+(Y2-Y1)*(X-X1)/(X2-X1)]
до Y=[Y1+(Y2-Y1)*(X-X1+1)/(X2-X1)]
Но при X1=X2, т.е. при вертикальной линии, эта прямая не может быть представлена такими линиями, поэтому нужно строить в этом сечении X=X1=X2 прямую от Y1 до Y2.
А при Y1=Y2, линию Y=Y1.
Здесь для построения сечения можно предложить следующий фрагмент программы
...
Var x1,x2,y1,y2: integer; …
{две координаты прямой, которую нужно изобразить на экране}
procedure harefxy(x,y:integer);
begin Gotoxy(x,y); Write(‘█’) end; …
Begin
Write('Введите через пробел координаты концов прямой:');
Read(x1,x2,y1,y2);{предполагается, что данные корректно вводятся, т.е. 0<x1,x2<81 и 0<y1,y2<25}
If Y1=Y2 Then {горизонталь}
If X1<X2 then
For X:=X1 to X2 do harefxy(x,y1)
else
For X:=X2 to X1 do harefxy(x,y1)
else
If X1=X2 Then {вертикаль}
If Y1<Y2 then
For Y:=Y1 to Y2 do harefxy(x1,y)
else
For Y:=Y2 to Y1 do harefxy(x1,y)
else
begin
If x1>x2 then
Begin
x1+=x2;x2:=x1-x2;x1:=x1-x2;
y1+=y2;y2:=y1-y2;y1:=y1-y2
end;
If abs((X1-X2)/(Y1-Y2))>=1 Then
for x:=x1 to x2 do
harefxy(x< y1+(y2-y1)*(x-x1) div (x2-x1))
Else
if y1<y2 then
for y:=y1 to y2 do
harefxy(x1+(x2-x1)*(y-y1) div (y2-y1),y)
End
...
end.
Игровые программы
На олимпиадах часто используются задачи связаннные с играми. Рассмотрим серию игр, в которых по очереди берутся спички или камни из кучи
Игра N1.
Правила игры:
— играют два игрока,
— задано 3 спички,
— игроки по очереди берут не более 3-х спичек,
— выигрывает тот, кто берет последний.
Выигрышная стратегия:
В этой игре первый игрок при желании забрав все спички выигрывает. В данном случае размер кучи для первого игрока может быть до трех спичек.
Игра N2.
Правила игры:
— играют два игрока,
— задано 4 спички,
— игроки по очереди берут не более 3-х спичек,
— выигрывает тот, кто берет последний.
Выигрышная стратегия:
В данном случае второй игрок при желании может выиграть после хода первого, забрав все спички.
Игра N3.
Правила игры:
— играют два игрока,
— задано 4*n спички,
— игроки по очереди берут не более 3-х спичек,
— выигрывает тот, кто берет последний.
Выигрышная стратегия:
В данном случае второй игрок при желании может выиграть после хода первого, забирая число спичек, дополняющих до четырех ход противника.
Игра N4.
Правила игры:
— играют два игрока,
— задано (k+1)*n спички,
— игроки по очереди берут не более k спичек,
— выигрывает тот, кто берет последний.
Выигрышная стратегия:
В данном случае второй игрок при желании может выиграть после хода первого, забирая число спичек, дополняющих до k+1 ход противника
Для усвоения игр можно их проводить в классе следующим образом
Принести спички в класс. Раздать в начале спички для Игры N4, затем предложить соседям по парте сыграть, После чего организовать соревнование по соседним партам в ряду. Затем по соседним рядам. Затем в конце концов по олимпийской системе победитель определиться в классе.
Данный метод игры позволит быстро провести турнир и держать учеников в определенной активности.
Если ученики осознают игру, можно организовать разбор метода решения. Если же метод решения не определится, то предложить сыграть с победителем. Что позволит повысить Ваш авторитет и возможно позволит ученикам увидеть выигрышную стратегию игры.
Если же и в этом случае ученики не определят стратегию, нужно перейти к рзбору Игр N1, N2 и N3.
После чего переходим к усложненой формулировке этих игр.
Игра N5.
Правила игры:
— играют два игрока,
— задано n спичек,
— игроки по очереди берут не более k спичек,
— выигрывает тот, кто берет последний.
Выигрышная стратегия:
При решении этой задачи решение нужно привести к правилам Игры N4. Для этого необходимо определить n кратно (k+1) или нет. Если n кратно (k+1), то это условия игры N4. Если же нет, то первым (n mod (k+1)) ходом можно привести к условиям игры N4.
Игра N6.
Правила игры:
— играют два игрока,
— задано n спичек,
— игроки по очереди берут не более k спичек,
— проигрывает тот, кто берет последний.
Выигрышная стратегия:
В данном случае нужно рассмотреть рассуждения игры N1 для четырех спичек. Если мы будем оставлять по одной спичкеЮ то мы выиграем. Поэтому выигрывает тот, кто после своего хода оставляет число спичек кратное (k+1) и еще 1. Поэтому для выигрыша необходимо определить (n mod (k+1))=1 или нет. Если равно, то надо ходить вторым и своим ходом обеспечивать это равенство, иначе надо сделать первый ход обепечивающий выполнение этого равенства, а затем играть как уже рассматривалось.
Игра «Гонки»
Как модификация данной игры можно рассмотреть игру «Гонки».
Правила игры:
— играют два игрока,
— задано n клеток на линии,
— игроки по очереди могут продвигать свою фишку от 1 до k клеток вправо или влево, не занимая место с фишкой противника и не перескакивая фишку противника,
— проигрывает тот, кто не сможет произвести ход.
В данной игре также как, в предыдущей, нужно привести свой ход к расстоянию между фишками кратному (k+1). Далее при движении навстречу наступит момент когда ваш ход приведет к встрече с фишкой противника. В последствии противник будет отходить к своему краю и наступит момент, когда он окажется на крайней позиции и не сможет произвести действие!
Игра «Ним»
Далее заданное множество камней можно разбить на кучи и третье правило можно сменить на то, что можно брать любое число только изодной кучи. Тогда это будет игра НИМ.
Правила игры:
— играют два игрока,
— задано n куч камней,
— игроки по очереди берут любое число камней изодной кучи,
— выигрывает тот, кто берет последний.
Выигрышная стратегия:
Для решения этой задачи используется двоичное представления чисел камней в каждой кучи: k1,k2,…kn. Далее их складывают поразрядно по модулю 2,
|
| Десятичное представление
| Двоичное представление
| сумма
|
| начало
| 5
| 3
| 2
| 111
| 11
| 10
| 110
|
| Ход1-1
| 4®1
| 3
| 2
| 1
| 11
| 10
| 0
|
| Ход1-2
| 1
| 2®1
| 2
| 1
| 1
| 2
| 10
|
| Ход2-1
| 1
| 1
| 2®0
| 1
| 1
| 0
| 0
|
| Ход2-2
| 1®0
| 1
| 0
| 0
| 1
| 0
| 1
|
| Ход3-1
| 0
| 1®0!
| 0
| 0
| 0
| 0
| 0!
|
При последнем ходе у выигравшего сумма равна 0. Поэтому для выигрыша надо после своего хода делать так, чтобы сумма получалась 0. Противник же всегда будет получать не 0. Исходя из этого, выбор первого хода определяется начальной суммой: если она оказывается равной 0, то нужно ходить вторым, иначе первым ходом нужно привести к нулевой ситуации и выиграть.
Вычисление полиномов
Рассмотрим несколько методов вычисления полиномов и оценку cкорости вычисления значения
Program polinom1;
{вычисление полинома= P0+P1 X+P2 X2 +...Pn-1 Xn-1 +Pn Xn }
Const n=8;
Var
i:integer;
p:array[0..n] of real;
natiga, {результат}
daraga:real; {степень}
Begin
read(x);
For i:=0 to n do read(p[i]);
natiga:=p[0];
| For i:=0 to n do
Begin { 1 }
daraga:=1;
For i:=1 to i do
daraga:=daraga*x
natiga:=natiga+daraga*p[i]
End;
| daraga:=1;
For i:=0 to n do
Begin { 2 }
natiga:=natiga+daraga*p[i];
daraga:=daraga*x
End;
|
write(natiga)
End.
При вычислении полинома в составном операторе {1} операции + и * выполняются 2n+n*(n+1)/2 раз.
При вычислении полинома в составном операторе {2} 3(n+1) раз выполняются операции + и * из них (n+1) операций + (более быстрые)..
Program polinom3; {вычисление полинома методом Горнера =P0+X(P1+X(P2+...X(Pn-1+ XPn)...)) }
Const n=8;
Var
i:integer;
p:array[0..n] of real;
natiga:real; {результат}
Begin
read(x);
For i:=0 to n do read(p[i]);
natiga:=0;
For i:=0 to n do natiga:=natiga*x+p[n-i] { 3 };
write(natiga)
End.
При вычислении полинома в операторе { 3 } 3(n+1) раз выполняются операции + и *. Из них 2(n+1) операций + (более быстрые).
Program polinom4; {вычисление полинома методом Горнера = P0+X(P1+X(P2+...X(Pn-1+XPn)...)) }
Const n=8;
Var
i:integer;
p:array[0..n] of real;
natiga:real; {результат}
Begin
read(x);
For i:=0 to n do read(p[i]);
natiga:=0;
For i:=0 downto n do natiga:=natiga*x+p[i] { 4 };
write(natiga)
End.
При вычислении полинома в операторе { 3 } 2(n+1) раз выполняются операции + и *. Из них n+1 операций + (более быстрые).
Факториал
Y=n!
Var y,n,i:integer;
Begin
Read(n);
| y:=1;
For i:=1 to n do y*=i;
| y:=n;
While n>1 do Begin
n-=1; y*=n
End;
|
write(y)
End.
Но при n>13 значение Y не представимо типом integer, поэтому можно применить int64. Но и здесь мы быстро дойдем до предела. Для этого типа n допустимо до 20.
Для решения этой задачи при больших значений необходимо самому написать фрагмент программы реализующий операцию умножения. Эта реализация требует определенный тип данных для представления получившегося числа. Так например, разряды этого числа могут представлятся как символы десятичных цифр в строковой переменной, либо как десятичные числа в массиве целых чисел. Далее рассмотрим вариант реализации через массив на языке Pascal и через длиную арифметику н языке Python.
| Pascal
| Python
|
| Const m=100;
Var I,n,j,k,kucher:integer;
factor:array[1..m]of integer;
Begin
Read(n);
For I:=1 to n do factor[I]:=0;
factor[100]:=1;
For I:=2 to n do {умножение}
Begin
Kucher:=0; // перенос
J:=i;
K:=m;
While j>0 do begin
factor[k]:=(factor[k]*(j mod 10)+kucher) mod 10;
Kucher:= (factor[k]*(j mod 10)+kucher) div 10;
J:=j div 10;
K-=1
end
End;
{печать результата}
K:=1;
While factor[k]=0 do k+=1;
While k<=m do begin
write(factor[k]);
k+=1;
end
End.
| n=int(input)
f=1
while n>1:
f*=n
print(n)
|
При m=100 n может принимать значение до 70. Если вектор фактор объявить array[1..m] of byte, то m может принимать значение до 64000. При появлении ограничений по аппаратной реализации арифметки арифметические задачи можно решать с помощью программной реализации необходимых арифметических операций.
Сортировка
Существуют сотни методов решения задач сортировки последовательности чисел.
Их можно классифицировать в следующие четыре типа:
1. универсальный комбинаторный метод – перебор;
2. исключая по одному элементы из процесса решения;
3. разбивая элементы по группам и отдельно решая задачу сортировки для подмножества, затем объединяя упорядоченные множества вместе;
4. сортировать с учетом особенностей заданной последовательсти элементов.
Рассмотрим примеры этих методов.
Program1 perebor;
Const k=4; { длина вектора}
Var variant:array[1..k] of 1..k; {перестановка}
Procedure perebor_i(j:Integer; {номер ответа в подстановке}
zapr:set of 1..k {множество выбранных элементов});
Var i:Integer; { подбираемый элемент}
Bar:integer; { }
Begin { в j-ую позицию перестановки}
Bar:=true;
For I:=2 to k do if varint[I-1]>variant[I] then bar:=false
if bar then
begin
For I:=1 to k do write(varint[I]);
Halt
End;
If j>0 Then
For i:=1 to k do
If not (i in zapr) Then
Begin variant[j]:=i;perebor_i(j-1,zapr+[i]) End;
End;
Begin perebor_i(k,[ ]) End.
Время работы при переборе равно n!.
Сортировка отделением элемента от последовательности.
Program maximum;
{Поиск максимального элемента и установка в конец}
Const n=10;
Var y,max,i,j:integer;
x:array[0..n] of real;
Begin
For i:=0 to n do Read(x[i]);
For j:=0 to n-1 do
Begin
max:=j;
For i:=j+1 to n do If (x[max]>x[i] then max:=i
{смена значений}
y:=x[max]; x[max]:=x[j]; x[j]:=y;
Write(x[j],' ')
End
End.
Время работы при данном методе равно n*(n-1)/2.
Упорядочение последовательности методом слияния.
Program slianie;
Const n=8;
Var x,y:Array[1..n] of >Integer;
i,j1,j2,h:Integer;
Procedure joint(i1,i2:integer);
{Слияние двух упорядоченных последовательностей.}
Var L,i,j:integer;
Begin
L:=0;
j:=0;
For i:=0 to 2*h-L do
If j>=h Then
Begin y[i1+i]:=x[i1+L]; L+=1 End
Else
If L>=h Then
Begin y[i1+i]:=x[i2+j];j+=1 End
Else
If x[i1+L]>x[i2+j] Then
Begin y[i1+i]:=x[i1+L]; L+=1 End
Else Begin y[i1+i]:=x[i2+j]; j+=1 End
End;
Begin
For i:=1 to n do Read(x[i]);
h:=1;
While h<n do
Begin
j1:=1;
For i:=1 to n do y[i]:=0;
While j1+h<=n do
Begin j2:=j1+h; joint(j1,j2); j1:=j1+2*h End;
If j1<=n Then
For i:=j1 to n do y[i]:=x[i];
x:=y;
h+=h
End;
Write('вектор=');
For i:=1 to n do Write(x[i]:3)
End.
Время работы при использовании метода слияния равно n log2n.
Последовательности с ограничениями
Program raznie;
{ Задана последовательность из различных значений. Для каждого элемента исходной последовательности определяется его порядковый номер в упорядоченной последовательности и ставится в соответствующее место упорядоченного массива.}
Const n=10;
Var i,j,k:Integer;
y,x:array[0..n] of Real;
Begin
For i:=0 to n do Read(x[i]);
For i:=0 to n do
Begin
k:=0;
For j:=0 to n do
If x[i]>x[j] then k:=k+1;
y[k]:=x[i]
End;
For i:=1 to n do Write(y[i])
End.
Время работы при данном методе равно n*n.
Program achkich;
{ Задана последовательность чисел X1,X2,...,Xn, где Xi принимает значения 1, 2 или 3. При решении этой задачи используется вектор R, где подсчитываются число элементов равных его индексу.}
Const n=10;
Var i,j:Integer;
r:array[1..3] of Integer;
x:array[1..n] of integer;
Begin
For i:=1 to n do Read(x[i]);
For i:=1 to 3 do R[i]:=0;
For i:=1 to n do
R[x[I]]:= R[x[I]]+1;
Write('Упорядоченная последовательность (');
For i:=1 to n do Write(x[I],' ');
Write(') = (')
For j:=1 to 3 do For i:=1 to r[j] do Write(j,' ');
Write(')')
End.
Время работы при данном методе равно n действий по вводу, счету числа значений от 1 до 3 и выводу.
13.2.  6. Фальшивая монета
6. Фальшивая монета
Решение этой задачи приведем на татарском языке.
I. n бер төрле акча бирелгән. Шуларның берсе ялган акча. Калганнардан ул үзенең авырлыгы белән аерылып тора. Шулай ук, ике аяклы үлчәү бирелгән. Кимендә ничә тапкыр үлчәүдә бу ялган акчаны ачыкларга була?
А)Ялган акчаның авырлыгы ким, йә артык булуы билгеле булса
Чишелеш:
1) n =2.
Бер үлчәүдә ачыклана. (ответ:1).
2) n =3.
Икесен алып үлчәүнең төрле аякларына куярга. Үлчәү авырлыгын бер итеп күрсәтсә өченчесе ялган була. Әгәр бер тигез булмаса ялган акчаны авырлыгыннан танып була.
Бер үлчәүдә ачыклана. (ответ: 1)
3) n =3 k.
Булган акчаны өчкә булеп икесен алып үлчәүнең төрле аякларына куярга. Үлчәү авырлыгын бер итеп күрсәтсә өченче өлешендә ялган акча була. Әгәр бер тигез булмаса ялган акчаны кайсы өлешендә булганын авырлыгыннан танып була.
Ялган акчалы өлештә тануны дәвам итәргә кирәк. Өчәү калгач бер үлчәүдә ялган акча таныла.
Ялган акча k үлчәүдә ачыклана. (ответ: k)
4) 3 k -1 < n <3 k.
Булган акчаны өчкә булеп [5] икесен алып үлчәүнең төрле аякларына куярга. Үлчәү авырлыгын бер итеп күрсәтсә өченче өлешендә ялган акча була. Әгәр бер тигез булмаса ялган акчаны кайсы өлешендә булганын авырлыгыннан танып була.
Ялган акча өченче өлештә булса 3 k -1 гә кадәр чын акча белән тулыландырып куярга кирәк.
Ялган акчалы өлештә А.3) тәгечә тануны дәвам итәргә кирәк.
Ялган акча k үлчәүдә ачыклана. (ответ: k)
Б) Әгәр ялган акчаның авырлыгы ким, йә артык булуы билгеле булмаган очрактагы чишелеш:
1) n =2.
мәсьәләне чишеп булмый. (ответ: нет решения)
2) n =3.
Икесен алып үлчәүнең төрле аякларына куярга.
Үлчәү авырлыгын бер итеп күрсәтсә өченчесе ялган була. Әгәр бертигез булмаса өченчесе чын акча була. Шуннан үлчәүдәге бер акчаны өченчесе белән алмаштырып үлчәргә кирәк. Үлчәү авырлыгын бер итеп күрсәтсә алынганы ялган була, Авырлыгы бертигез булмаса үлчәүдән калганы ялган була.
Өч акча арасында ике үлчәүдә ялган акча табыла. (ответ: 2)
3) n =4.
Икесен алып үлчәүнең төрле аякларына куярга.
Үлчәү авырлыгын бертигез итеп күрсәтсә ялган акча үлчәнмәгән өлешендә була. Шуларның берсен чын акчага алмаштырып үлчәп алырга кирәк. Үлчәү авырлыгын бер итеп күрсәтсә үлчәүгә салынмаган акча ялган була. Бертигез булмаса үлчәүгә соңгы салынган акча ялган була.
Әгәр беренче үлчәүдә бертигез булмаса үлчәүдәге бер акчаны өченчесе белән алмаштырып үлчәргә кирәк. Үлчәү авырлыгын бертигез итеп күрсәтсә үлчәүдән алынган акча ялган була, Авырлыгы бер тигез булмаса үлчәүдә калганы ялган акча була.
Дүрт акча арасында ике үлчәүдә ялган акча табыла. (ответ: 2)
4) n =5.
Икешәрны алып үлчәүнең төрле аякларына куярга. (1,2? 3,4)
Үлчәү авырлыгын бертигез итеп күрсәтсә ялган акча бишенчесе була.
Әгәр беренче үлчәүдә бертигез булмаса (1,2 > 3,4) үлчәүдәге 4нче акчаны алып куеп 5нче акчаны 2нче урнына, 2нчене 4нче урнына куеп үлчәргә кирәк. Үлчәү авырлыгын бертигез итеп күрсәтсә алынган 4нче акча ялган була, Әгәр 1>,5 > 2>,3<,булса 1> йә 3< ялган акча була. Шуларның берәрсен төшереп калдырып үлчәсәк соңгысы ачыклана. Әгәр 1>,5 < 2>,3< булса 2нчесе ялган акча була. Әгәр 1>,5 = 2>,3< булса 4нчесе ялган акча була.
Биш акча арасында өч үлчәүдә ялган акча табыла. (ответ: 3)
5) n =6,7,8,9 булганда җавабы шулай ук 3 үлчәүдә ачыклана. (ответ: 3)
6) n =10.
Булган акчаны өчәрләп төркемнәргә булеп чыгырга кирәк:
1,2,3; 4,5,6; 7,8,9; 10
Ике төркемен үлчәү аякларына салып үлчәргә кирәк. Бер тигез булса калган дүртесе ике үлчәүдә ачыклана.
Бер тигез булмаса 1,2,3 > 4,5,6 1нче белән 6нчы акчаны алып куеп 2,3,4,5? 7,8,9,10 үлчәп > булса 4,5 арасында ялган акча була. Әгәр < булса 2,3 арасында ялган акча була. Өченче үлчәүдә ялган акчаны ачыклар өчен берсен чын акча белән алмаштырып үлчәп алырга кирәк. Бертигез булса алып куелган акча ялган була. Бертигез булмаса калган акча ялган булып чыга.
Икенче үлчәүдә бертигез булса 1нче белән 6нчы акча ялган була ансын бер үлчәүдә ачыклап була.
Беренче үлчәүдә бертигез булса калган дүрт акча арасында ике үлчәүдә акча табыла.
10 акча арасында өч үлчәүдә ялган акча табыла. (ответ: 3)
7) n =11.
Булган акчаны өчәрләп төркемнәргә булеп чыгырга кирәк:
1,2,3,4; 5,6,7,8; 9,10,11
1,2,3,4? 5,6,7,8 – 1нче үлчәү
=1 булса 9,10,11 арасында ике үлчәү белән ачыклап була.
>1 булса 2,3,5,6? 4,9,10,11 – 2нче үлчәү.
>1=2 булса ялган акча 1,7,8 арасында була.
1,7? 9,10 3нче үчәүдә =3 булса 8нче акча ялган була. >3 булса 1нче акча ялган була. <3 булса 7нче акча ялган була.
>1>2 булса ялган акча 2,3 арасында була. Бер үлчәүдә ялган акча ачыклана.
>1<2 булса ялган акча 5,6,4 арасында була. Өченче үлчәүдә 6,4? 1,2 карала. =3 булса 5нче акча ялган була. >3 булса ялган акча 6нчы акча була. <3 булса ялган акча 4нче акча ялган була.
11 акча арасында өч үлчәүдә ялган акча табыла. (ответ: 3)
8) n =12.
Булган акчаны өчәрләп төркемнәргә булеп чыгырга кирәк:
1,2,3,4; 5,6,7,8; 9,10,11,12
11дәгечә үлчәп чыгып өч үлчәүдә ялган акча табыла. (ответ: 3)
9) n =3 k.
Булган акчаны өчкә булеп икесен алып үлчәүнең төрле аякларына куярга.
Үлчәү авырлыгын бер итеп күрсәтсә өченчесе ялган була. Үлчәүдәге бер өлешен алып ялган акчалы элешкә алмаштырып үлчәп алгач ялган акчаның авырлыгыким йәки артык булганын ачыклап куябыз. Соңыннан А.3) тәртибе буенча үлчәүне шул өлеш белән дәвам итәргә кирәк.
Әгәр бертигез булмаса өченче өлештә чын акча була. Шуннан үлчәүдәге бер акчаны өченче өлеш белән алмаштырып үлчәсәк шулай ук шулай ук кайсы өлештә ялган акча булганы һәм аның авылыгы ким йәки артык булганы ачыклана. Соңыннан А.3) тәртибе буенча үлчәүне шул өлеш белән дәвам итәргә кирәк.
3 k акча арасында ялган акча k +1 үлчәүдә ачыклана. (ответ: k+1)
10) 3 k -1 < n <3 k. (3 k -1 < n <=3 k -1 +3 k -2)
N акча арасында ялган акча k үлчәүдә ачыклана. (ответ: k)
11) 3 k -1 < n <3 k. (3 k -1 +3 k -2 < n <3 k)
Бу мәсьәләне чишкәндә Б.9) һәм А.3) тәгечә чишеп барырга кирәк.
N акча арасында ялган акча k +1 үлчәүдә ачыклана. (ответ: k+1)
Әзрәк мәсьәлә шартларын үзгәртеп карыйк.
II.Дано n мешков денег одного достоинства. Один из мешков набит фальшивыми монетами отличающихся от настоящих на один грамм. Каким образом одним взвешиванием на электронных весах, определяющих вес с точностью в один грамм определить мешок с фальшивыми монетами?
Чишелеш:
Бу очракта һәр бер капчыкны санап чыгып шул санга туры килгән капчыктан акча санын алып бөтенсен үчәргә кирәк. Нәтиҗәдә үлчәнгән акчаның 1 a +2 a +3 a +4 a … + la + l +…+ na = n (n +1) a /2+ l авырлыгы була. а – акчаның авырлыгы итеп карала. n (n +1) a /2 санап чыгып l не исәпләп чыккач ялган акчалы капчыкны танырга була.
Бу мәсьәләне чишкәндә ялган акчалы капчыкны бер үлчәүдә танып була.
III.На базар один крестъянин привез 80-ти колограммовые мешки с ячменью. На базаре торговля зерном идет килограммами. Для торговли на равноплечных весах крестьянину надо заказать у кузнеца гири. Стоимость одной гири – мешок зерна. Какое минимальное число гирей нужно заказать, чтобы одним взвешиванием можно было бы отвесить требуемый вес.
Решение:
Часто, ответом звучит набор 1, 2, 4, 8, 16, 32, 64 кг гирь, позволяющих определить вес зерна как сумму степеней 2 на равноплечных весах. В этом случае надо заказать 7 гирей.
Но на равноплечных весах гири можно размещать с двух сторон. [6] Вместо 2 кг гири можно заказать3кг:
1 кг зерна= 1 кг гиря,
2 кг зерна + 1 кг гиря = 3 кг гиря,
3 кг зерна = 3 кг гиря,
4 кг зерна = 3 кг гиря + 1 кг гиря.
Теперь уже вместо 4 кг можно заказать более тяжелую гирю. Или с помощью 8 к г, которая в нашем наборе есть, можно взввесить либо вместо него 9 кг
5 кг зерна + 3 кг гиря = 8 кг гиря ó 5 кг зерна + 3 кг + 1 кг гиря = 9 кг гиря,
6 кг зерна + 3 кг гиря = 8 кг гиря + 1 кг гиря ó 6 кг зерна + 3 кг гиря = 9 кг,
7 кг зерна + 1 кг гиря = 8 кг гиря ó 7 кг зерна + 3 кг гиря = 9 кг гиря + 1 кг,
8 кг зерна = 8 кг гиря ó 8 кг зерна +1 кг гиря = 9 кг гиря.
9 кг зерна = 9 кг гиря
10 кг зерна = 9 кг гиря + 1 кг гиря,
11 кг зерна + 1 кг гиря = 9 кг гиря + 3 кг гиря,
12 кг зерна = 9 кг гиря + 3 кг гиря,
13 кг зерна = 9 кг гиря + 3 кг гиря + 1 кг гиря.
Вместо 16 кг гири можно взять 27 кг,
14 кг зерна + 1 кг гиря + 9 кг гиря + 3 кг гиря = 27 кг гиря.
С помощью этих четырех гирь (1,3,9,27) можно взесить до 40 к г.
А с 41 до 80 можно определять зерна,который можно оставить. Оставляемыый вес от 1 до 40 кг.
Шуның белән сатучыга 4 гер җитә. Сатучы җиһазлар өчен 5 сум түләп сату итә ала.






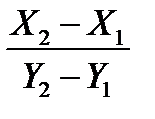 < 1, то у этой прямой получится следующий вид
< 1, то у этой прямой получится следующий вид т.е. проводник размыкается из-за того, что между ступенями расстояние больше 1.
т.е. проводник размыкается из-за того, что между ступенями расстояние больше 1. 6. Фальшивая монета
6. Фальшивая монета


