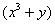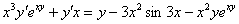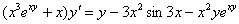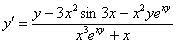Это правило остается в силе, если промежуточных аргументов несколько. Так, если у=ƒ(u), u=φ(ν), ν=g(х), то у'х=у'u•u'ν•ν'х. Пусть у=ƒ(х) и х=φ(у) — взаимно обратные функции.
Теорема 20.6. Если функция у=ƒ(х) строго монотонна на интервале (a;b) и имеет неравную нулю производную ƒ'(х) в произвольной точке этого интервала, то обратная ей функция х=φ(у) также имеет производную φ'(у) в соответствующей точке, определяемую равенством
 Рассмотрим обратную функцию х=φ(у). Дадим аргументу у приращение ∆у 0. Ему соответствует приращение ∆х обратной функции, причем ∆х 0 в силу строгой монотонности функции у=ƒ(х). Поэтому можно записать
Рассмотрим обратную функцию х=φ(у). Дадим аргументу у приращение ∆у 0. Ему соответствует приращение ∆х обратной функции, причем ∆х 0 в силу строгой монотонности функции у=ƒ(х). Поэтому можно записать
 Если ∆у→0, то в силу непрерывности обратной функции приращение ∆х→0. И так как
Если ∆у→0, то в силу непрерывности обратной функции приращение ∆х→0. И так как
 то из (20.7) следуют равенства
то из (20.7) следуют равенства
 Таким образом, производная обратной функции равна обратной величине производной данной функции. Правило дифференцирования обратной функции записывают так:
Таким образом, производная обратной функции равна обратной величине производной данной функции. Правило дифференцирования обратной функции записывают так:

<< Пример 20.3
Найти производную функции у=log23tg x4. Решение: Данная функция является сложной. Ее можно представить в виде цепочки «простых» функций: у=u3, где u=Iog2z, где z=tgq, где q=х4. По правилу дифференцирования сложной функции (у'х=y'u•u'z•z'q•q'x) получаем:

Производные основных элементарных функций.

25. Логарифмическое дифференцирование.
ри вычислении производной от логарифма произведения, частного, степени или корня, для упрощения нахождения производной проводят предварительное преобразование (см. Пример 10(и)).
В ряде случаев для нахождения производной целесообразно заданную функцию сначала прологарифмировать (по умолчанию имеется в виду натуральный логарифм). Затем найти производную от этого логарифма и по ней отыскать производную от заданной функции. Такой прием называется логарифмическим дифференцированием.
Метод логарифмического дифференцирования позволяет легко найти производную показательно-степенной функции вида
 ,
,
где 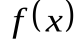 и
и  – дифференцируемые функции аргумента
– дифференцируемые функции аргумента  .
.
Пример 14.
Найти производную функции  .
.
Решение.
Прологарифмируем обе части функции и преобразуем выражение:
 .
.
Теперь дифференцируем уравнение, как неявно заданную функцию:
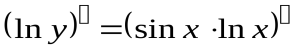 ;
;
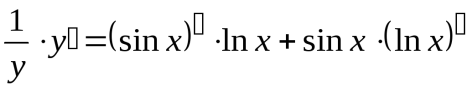 ;
;
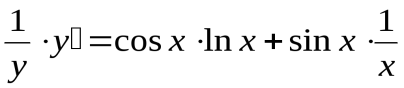 ;
;
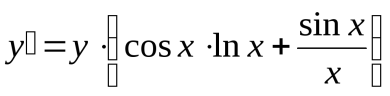 ;
;
Так как  , то окончательно получаем:
, то окончательно получаем:
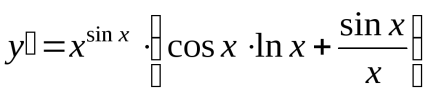
26. Производные неявных функций. Что такое неявная функция? Давайте сначала вспомним: Функция одной переменной 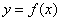 –это правило, по которому каждому значению независимой переменной
–это правило, по которому каждому значению независимой переменной 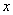 соответствует одно и только одно значение функции
соответствует одно и только одно значение функции 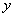 .
.
Переменная 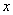 называется независимой переменной или аргументом.
называется независимой переменной или аргументом.
Переменная 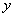 называется зависимой переменной или функцией.
называется зависимой переменной или функцией.
До сих пор мы рассматривали функции, заданные в явном виде. Что это значит? Устроим разбор полётов на конкретных примерах.
Рассмотрим функцию 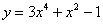
Мы видим, что слева у нас одинокий «игрек», а справа – только «иксы». То есть, функция 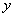 в явном виде выражена через независимую переменную
в явном виде выражена через независимую переменную 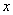 .
.
Рассмотрим другую функцию: 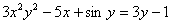
Здесь переменные 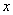 и
и 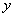 расположены «вперемешку». Причем никакими способами невозможно выразить «игрек» только через «икс». Что это за способы? Перенос слагаемых из части в часть со сменой знака, вынесение за скобки, перекидывание множителей по правилу пропорции и др. Перепишите равенство
расположены «вперемешку». Причем никакими способами невозможно выразить «игрек» только через «икс». Что это за способы? Перенос слагаемых из части в часть со сменой знака, вынесение за скобки, перекидывание множителей по правилу пропорции и др. Перепишите равенство 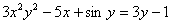 и попробуйте выразить «игрек» в явном виде:
и попробуйте выразить «игрек» в явном виде: 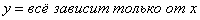 . Можно крутить-вертеть уравнение часами, но у вас этого не получится.:
. Можно крутить-вертеть уравнение часами, но у вас этого не получится.: 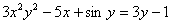 – пример неявной функции.
– пример неявной функции.
В курсе математического анализа доказано, что неявная функция существует (однако не всегда), у неё есть график (точно так же, как и у «нормальной» функции). У неявной функции точно так же существует первая производная, вторая производная и т.д. Как говорится, все права секс-меньшинств соблюдены.
. Пример 1 Найти производную от функции, заданной неявно 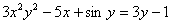
1) На первом этапе навешиваем штрихи на обе части:
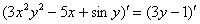
2) Используем правила линейности производной 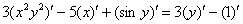
3) Непосредственное дифференцирование.
Как дифференцировать 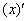 и
и 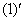 совершенно понятно. Что делать там, где под штрихами есть «игреки»?
совершенно понятно. Что делать там, где под штрихами есть «игреки»?
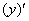 – просто до безобразия, производная от функции равна её производной:
– просто до безобразия, производная от функции равна её производной: 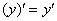 .
.
Как дифференцировать 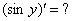
Здесь у нас сложная функция. Почему? Вроде бы под синусом всего одна буква «игрек». Но, дело в том, что всего одна буква «игрек» – САМА ПО СЕБЕ ЯВЛЯЕТСЯ ФУНКЦИЕЙ (см. определение в начале урока). Таким образом, синус – внешняя функция, 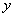 – внутренняя функция. Используем правило дифференцирования сложной функции
– внутренняя функция. Используем правило дифференцирования сложной функции 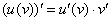 :
:
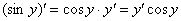 Произведение дифференцируем по обычному правилу
Произведение дифференцируем по обычному правилу 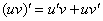 :
:
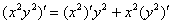
Обратите внимание, что 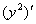 – тоже сложная функция, любой «игрек с наворотами» – сложная функция:
– тоже сложная функция, любой «игрек с наворотами» – сложная функция:
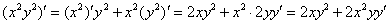
Само оформление решения должно выглядеть примерно так:
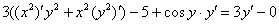
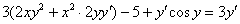
Если есть скобки, то раскрываем их: 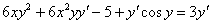
4) В левой части собираем слагаемые, в которых есть «игрек» со штрихом. В правую часть – переносим всё остальное:
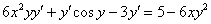 5) В левой части выносим производную
5) В левой части выносим производную 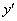 за скобки:
за скобки:
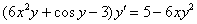 6) И по правилу пропорции сбрасываем эти скобки в знаменатель правой части:
6) И по правилу пропорции сбрасываем эти скобки в знаменатель правой части:
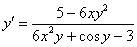 Производная найдена. Готово.
Производная найдена. Готово.
Интересно отметить, что в неявном виде можно переписать любую функцию. Например, функцию 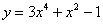 можно переписать так:
можно переписать так: 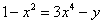 . И дифференцировать её по только что рассмотренному алгоритму. На самом деле фразы «функция, заданная в неявном виде» и «неявная функция» отличаются одним смысловым нюансом. Фраза «функция, заданная в неявном виде» более общая и корректная,
. И дифференцировать её по только что рассмотренному алгоритму. На самом деле фразы «функция, заданная в неявном виде» и «неявная функция» отличаются одним смысловым нюансом. Фраза «функция, заданная в неявном виде» более общая и корректная, 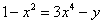 – эта функция задана в неявном виде, но здесь можно выразить «игрек» и представить функцию в явном виде. Под фразой «неявная функция» понимают «классическую» неявную функцию, когда «игрек» выразить нельзя.
– эта функция задана в неявном виде, но здесь можно выразить «игрек» и представить функцию в явном виде. Под фразой «неявная функция» понимают «классическую» неявную функцию, когда «игрек» выразить нельзя.
Второй способ решения
Внимание! Со вторым способом можно ознакомиться только в том случае, если Вы умеете уверенно находить частные производные. Начинающие изучать математический анализ и чайники, пожалуйста, не читайте и пропустите этот пункт, иначе в голове будет полная каша.
Найдем производную неявной функции 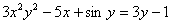 вторым способом.
вторым способом.
Переносим все слагаемые в левую часть: 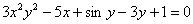
И рассматриваем функцию двух переменных: 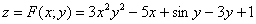
Тогда нашу производную можно найти по формуле 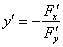
Найдем частные производные:
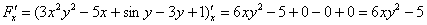
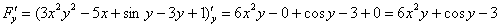
Таким образом:
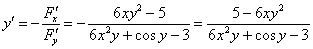
Второй способ решения позволяет выполнить проверку. Но оформлять им чистовой вариант задания нежелательно, поскольку частные производные осваивают позже, и студент, изучающий тему «Производная функции одной переменной», знать частные производные как бы еще не должен.
Рассмотрим еще несколько примеров.
Пример 2
Найти производную от функции, заданной неявно 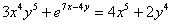
Навешиваем штрихи на обе части:
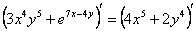
Используем правила линейности:
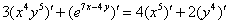
Находим производные:
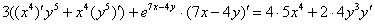
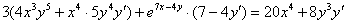
Раскрываем все скобки:
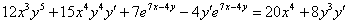
Переносим все слагаемые с 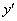 в левую часть, остальные – в правую часть:
в левую часть, остальные – в правую часть:
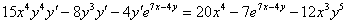
У В левой части выносим 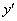 за скобку:
за скобку:
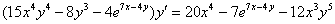
Окончательный ответ:
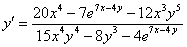
Пример 4
Найти производную от функции, заданной неявно 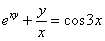
Заключаем обе части под штрихи и используем правило линейности:
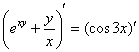
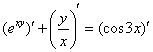
Дифференцируем, используя правило дифференцирования сложной функции 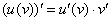 и правило дифференцирования частного
и правило дифференцирования частного 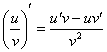 :
:
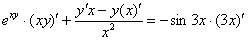
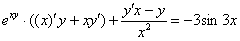
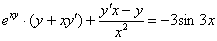
Раскрываем скобки:
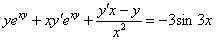
Теперь нам нужно избавиться от дроби. Это можно сделать и позже, но рациональнее сделать сразу же. В знаменателе дроби находится 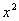 . Умножаем каждое слагаемое каждой части на
. Умножаем каждое слагаемое каждой части на 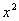 . Если подробно, то выглядеть это будет так:
. Если подробно, то выглядеть это будет так:
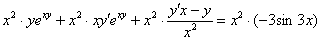

Иногда после дифференцирования появляется 2-3 дроби. Если бы у нас была еще одна дробь, например, 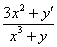 , то операцию нужно было бы повторить – умножить каждое слагаемое каждой части на
, то операцию нужно было бы повторить – умножить каждое слагаемое каждой части на 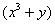
Далее алгоритм работает стандартно, после того, как все скобки раскрыты, все дроби устранены, слагаемые, где есть «игрек штрих» собираем в левой части, а в правую часть переносим всё остальное:
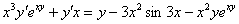
В левой части выносим 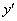 за скобку:
за скобку:
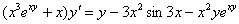
Окончательный ответ:
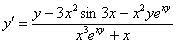
27. Параметрически заданные функции и их дифференцирование.



 Рассмотрим обратную функцию х=φ(у). Дадим аргументу у приращение ∆у 0. Ему соответствует приращение ∆х обратной функции, причем ∆х 0 в силу строгой монотонности функции у=ƒ(х). Поэтому можно записать
Рассмотрим обратную функцию х=φ(у). Дадим аргументу у приращение ∆у 0. Ему соответствует приращение ∆х обратной функции, причем ∆х 0 в силу строгой монотонности функции у=ƒ(х). Поэтому можно записать Если ∆у→0, то в силу непрерывности обратной функции приращение ∆х→0. И так как
Если ∆у→0, то в силу непрерывности обратной функции приращение ∆х→0. И так как то из (20.7) следуют равенства
то из (20.7) следуют равенства Таким образом, производная обратной функции равна обратной величине производной данной функции. Правило дифференцирования обратной функции записывают так:
Таким образом, производная обратной функции равна обратной величине производной данной функции. Правило дифференцирования обратной функции записывают так:


 ,
,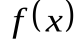 и
и  – дифференцируемые функции аргумента
– дифференцируемые функции аргумента  .
. .
. .
.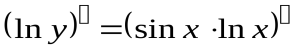 ;
;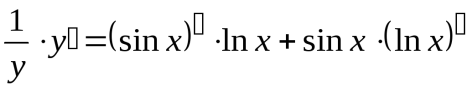 ;
;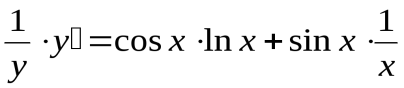 ;
;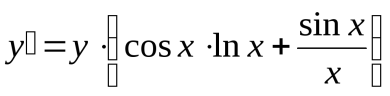 ;
;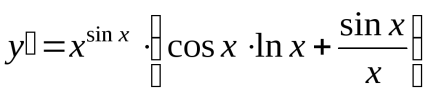
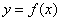 –это правило, по которому каждому значению независимой переменной
–это правило, по которому каждому значению независимой переменной 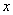 соответствует одно и только одно значение функции
соответствует одно и только одно значение функции 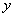 .
.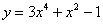
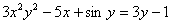
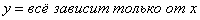 . Можно крутить-вертеть уравнение часами, но у вас этого не получится.:
. Можно крутить-вертеть уравнение часами, но у вас этого не получится.: 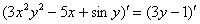
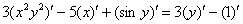
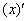 и
и 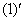 совершенно понятно. Что делать там, где под штрихами есть «игреки»?
совершенно понятно. Что делать там, где под штрихами есть «игреки»?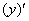 – просто до безобразия, производная от функции равна её производной:
– просто до безобразия, производная от функции равна её производной: 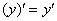 .
.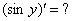
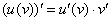 :
: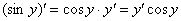 Произведение дифференцируем по обычному правилу
Произведение дифференцируем по обычному правилу 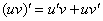 :
: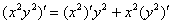
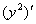 – тоже сложная функция, любой «игрек с наворотами» – сложная функция:
– тоже сложная функция, любой «игрек с наворотами» – сложная функция: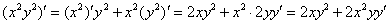
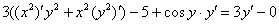
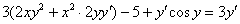
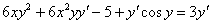
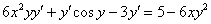 5) В левой части выносим производную
5) В левой части выносим производную 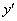 за скобки:
за скобки: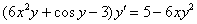 6) И по правилу пропорции сбрасываем эти скобки в знаменатель правой части:
6) И по правилу пропорции сбрасываем эти скобки в знаменатель правой части: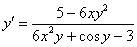 Производная найдена. Готово.
Производная найдена. Готово.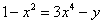 . И дифференцировать её по только что рассмотренному алгоритму. На самом деле фразы «функция, заданная в неявном виде» и «неявная функция» отличаются одним смысловым нюансом. Фраза «функция, заданная в неявном виде» более общая и корректная,
. И дифференцировать её по только что рассмотренному алгоритму. На самом деле фразы «функция, заданная в неявном виде» и «неявная функция» отличаются одним смысловым нюансом. Фраза «функция, заданная в неявном виде» более общая и корректная, 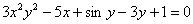
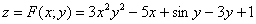
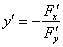
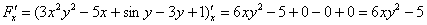
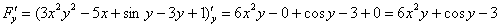
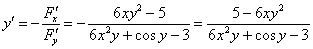
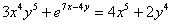
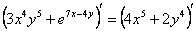
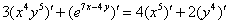
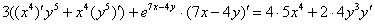
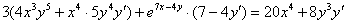
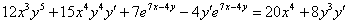
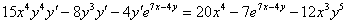
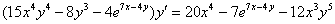
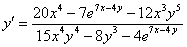
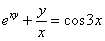
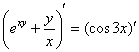
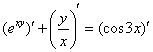
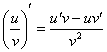 :
: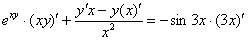
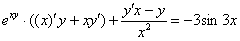
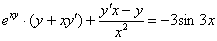
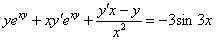
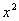 . Умножаем каждое слагаемое каждой части на
. Умножаем каждое слагаемое каждой части на 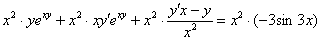

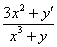 , то операцию нужно было бы повторить – умножить каждое слагаемое каждой части на
, то операцию нужно было бы повторить – умножить каждое слагаемое каждой части на