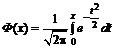Вопросы для самопроверки
1. Что мы понимаем под событием?
2. Дайте классическое определение вероятности.
3. Что называется суммой двух событий?
4. Сформулируйте теоремы сложения и умножения вероятностей.
5. Какая случайная величина называется дискретной?
6. Назовите числовые характеристики дискретной случайной величины и сформулируйте их определения.
Рекомендации к решению заданий
Формулы комбинаторики.
1. Пять студентов приобрели пять билетов в театр. Сколькими способами студенты могут разместиться на приобретенных местах?
Число способов размещения студентов в театре равно числу перестановок из пяти элементов: 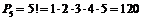 .
.
2. Сколько трехзначных чисел можно составить из пяти различных цифр, если каждая цифра входит в число по одному разу?
Число трехзначных чисел из пяти цифр равно числу размещений из пяти элементов по три: 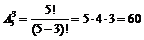 .
.
3. Пять студентов приобрели три билета в театр. Сколькими способами можно выбрать делегацию студентов в театр?
Число всевозможных способов выбора делегации в театр из пяти человек на три места равно числу сочетаний из пяти элементов по три:
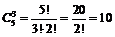 .
.
Классическое определение вероятности.
4. Пусть на машинном дворе стоят 17 грузовых машин, семь из которых имеют грузоподъемность 1,5 т, шесть –3 т и четыре – 5 т. За некоторым грузом отправляются две наудачу взятые машины. Какова вероятность того, что отправленные машины заберут весь груз, если его масса 6,5 т?
Введем событие А – отправленные машины заберут весь груз. Найдем вероятность события А по формуле классического определения вероятности
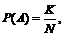
где N – число всевозможных исходов испытания;
K – число исходов, благоприятствующих появлению события А.
Число способов, которыми можно отправить две машины из имеющихся 17, равно 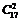 . Значит,
. Значит, 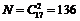 .
.
Но не каждая пара может забрать 6,5 т груза. Груз будет весь взят, если будут отправлены: или одна полуторатонная и одна пятитонная машины (таких способов 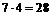 ); или одна трехтонная и одна пятитонная машины (таких способов
); или одна трехтонная и одна пятитонная машины (таких способов 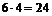 ); или две пятитонные машины (таких способов
); или две пятитонные машины (таких способов 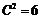 ). Итак,
). Итак, 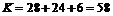 .
.
Следовательно, 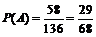 .
.
Теоремы сложения и умножения вероятностей.
5. В куче картофеля 20 % клубней, пораженных болезнью. Определить вероятность того, что клубень, взятый случайным образом из кучи картофеля, окажется непораженным.
Введем событие А – взятый клубень поражен болезнью. Тогда противоположное событие 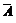 – клубень не поражен болезнью. Из условия задачи принимаем
– клубень не поражен болезнью. Из условия задачи принимаем 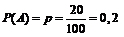 . Тогда найдем противоположного события к А
. Тогда найдем противоположного события к А 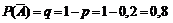 .
.
6. В поле работают три комбайна. Вероятность того, что в течение смены первый комбайн не потребует ремонта, равна 0,9, второй – 0,6, третий – 0,7. Найти вероятность того, что в течение смены не потребует ремонта: а) два комбайна; б) хотя бы один комбайн.
Введем события:
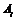 – в течение смены
– в течение смены 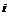 - й комбайн не потребует ремонта;
- й комбайн не потребует ремонта;
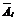 – в течение смены
– в течение смены 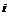 - й комбайн потребует ремонта,
- й комбайн потребует ремонта, 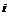 =1, 2, 3.
=1, 2, 3.
Тогда 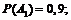
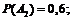
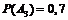 .
.
Найдем 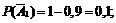
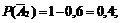
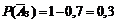 .
.
а) обозначим событие B – в течение смены два комбайна не потребуют ремонта. Тогда событие B можно представить в виде
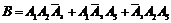 .
.
Написанные слагаемые представляют собой несовместные события, поэтому по теореме сложения вероятностей несовместных событий имеем:
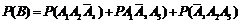 .
.
Поскольку события 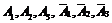 независимые, то, применяя теорему умножения вероятностей независимых событий, имеем:
независимые, то, применяя теорему умножения вероятностей независимых событий, имеем:
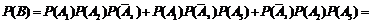 =
= 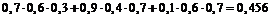 ;
;
б) обозначим событие С – в течение смены хотя бы один комбайн не потребует ремонта.
Если в результате испытания могут появиться три события, то появление хотя бы одного из этих событий означает наступление либо одного, либо двух, либо трех событий.
Вероятность появления хотя бы одного из независимых в совокупности событий А 1, А 2,…, А n равна разности между единицей и произведением вероятностей противоположных событий 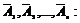
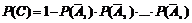 .
.
Следовательно, 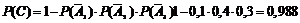 .
.
Условная вероятность событий.
7. Многолетними наблюдениями установлено, что в некоторой местности в сентябре 10 дней бывают дождливыми. Определить вероятность того, что первые 3 дня не будут дождливыми.
Обозначим события:
А 1 – 1 сентября не будет дождливым днем;
А 2 –2 сентября не будет дождливым днем;
А 3– 3 сентября не будет дождливым днем;
В – первые 3 дня не будут дождливыми.
Тогда 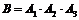 . События
. События 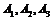 являются зависимыми, так как проходит один день и изменяется и общее количество дней, и количество недождливых дней.
являются зависимыми, так как проходит один день и изменяется и общее количество дней, и количество недождливых дней.
По теореме умножения вероятностей зависимых событий имеем:

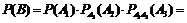
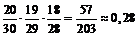 .
.
8. На откорм поставлено 100 бычков, из которых 30 – породы «а», 25 – породы «b» и 45 – породы «с». Вероятность того, что бычок породы «а» даст суточный привес более 500 г, равна 0,7, для пород «b» и «с» она равна 0,6 и 0,5 соответственно. Для контрольного взвешивания наудачу взят один бычок. Какова вероятность того, что его привес будет более 500 г?
Введем события (гипотезы):
Н 1–взят бычок породы «а»;
Н 2 – взят бычок породы «b»;
Н 3 – взят бычок породы «с».
События Н 1, Н 2, Н 3 – попарно несовместные, так как взят только один бычок, и единственно возможные, так как пород, отличных от «а», «b», «c», во взятой совокупности бычков нет. Интересующее нас событие – привес взятого бычка более 500 г – обозначим через А. Тогда
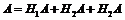 .
.
Применим формулу полной вероятности
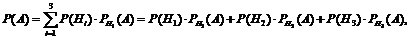
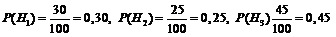 .
.
Вероятности 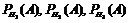 даны в условии задачи. Остается вычислить искомую вероятность:
даны в условии задачи. Остается вычислить искомую вероятность:
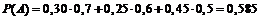 .
.
9. На откорме стоят те же бычки. Для контроля взвешен один наудачу взятый бычок. Какова вероятность, что этот бычок: породы «а»; породы «b»; породы «с», если его привес более 500 г?
Необходимо найти 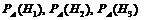 . Воспользуемся формулами Байеса, причем Р (А) мы нашли выше.
. Воспользуемся формулами Байеса, причем Р (А) мы нашли выше.
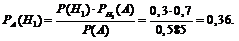
Аналогично 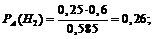
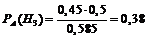 .
.
Повторные независимые испытания.
10. Предположим, что в случае распространения некоторой эпидемии корова некоторой породы заболеет с вероятностью 0,3. Найти вероятность того, что из десяти коров этой породы заболеют не более четырех, если указанная эпидемия распространяется.
Для решения задачи представим интересующее нас событие B (заболеют не более четырех коров) в виде суммы несовместных событий 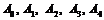
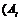 –заболеет ровно
–заболеет ровно 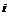 коров из десяти,
коров из десяти, 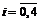 ).
).
Тогда 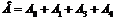 , а вероятность этого события можно найти по формуле
, а вероятность этого события можно найти по формуле
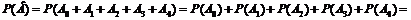
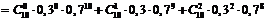
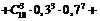
+ 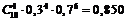 .
.
11. Некоторое хозяйство на зимний период поставило 1000 овец. Известно, что падеж овец за зимний период составляет 2 %. Найти вероятность того, что за зимний период погибнет: а) ровно 15 овец; б) от 10 до 30 овец.
а) воспользуемся формулой Пуассона при 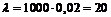 :
:
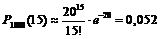 .
.
В данном случае можно было бы воспользоваться и локальной формулой Муавра–Лапласа:
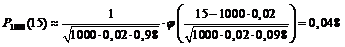 .
.
Разность полученных результатов объясняется тем, что использовались формулы приближенного вычисления вероятностей.
б) здесь будем использовать интегральную формулу Муавра–Лапласа:
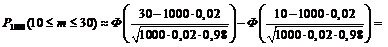 =
= 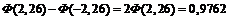 .
.
Закон распределения и числовые характеристики дискретной случайной величины.
12. Анализируется группа из десяти коров. Известно, что в этой группе есть четыре рекордсменки. Из группы случайно отбирают пять коров. Записать закон распределения случайной величины Х – числа рекордсменок среди отобранных коров. Получить ее функцию распределения F(x). Построить многоугольник распределения и функцию распределения случайной величины Х. Определить вероятность того, что среди отобранных будет не менее трех рекордсменок и найти ее числовые характеристики.
Число рекордсменок, попавших в группу отбора, может быть 0, 1, 2, 3, 4. Составим закон распределения случайной величины Х. Для этого каждому из ее значений поставим в соответствие вероятность их появления. Заметим, что рассматриваемые события попарно несовместные, поэтому найдем вероятности, руководствуясь классическим определением вероятности:
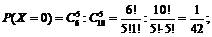
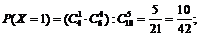
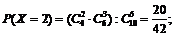
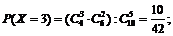
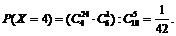
Тогда закон распределения рассматриваемой случайной величины может быть представлен в виде следующей таблицы:
Найдем значения функции распределения F(x) при различных значениях ее аргумента х. Ясно, что случайная величина Х принять отрицательные значения не может. Это значит, что:
для 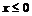 событие
событие 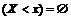 (невозможное);
(невозможное);
для 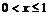 событие
событие 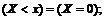
для 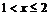 событие
событие 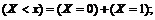
для 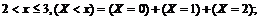
для 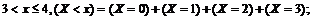
для 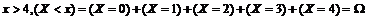 (достоверное событие).
(достоверное событие).
Поэтому для получения функции распределения случайной величины Х составим таблицу накопленных вероятностей:
Тогда функция распределения случайной величины Х будет иметь вид
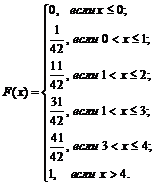
Построим многоугольник распределения (рис. 5, а) и функцию распределения (рис. 5, б) случайной величины.
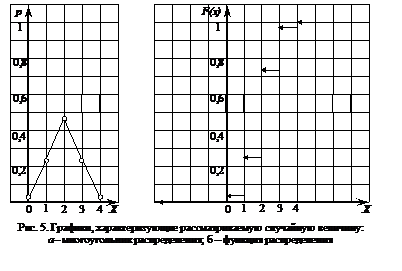
Вероятность того, что среди отобранных будет не менее трех рекордсменок, найдем, воспользовавшись равенством
P (x 1≤ X ≤ x 2)= F (x 2) – F (x 1).
Тогда P (3≤ X ≤¥)= F (¥) – F (3)=1– 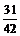 =
= 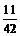 .
.
Найдем математическое ожидание случайной величины X:
M (X)= 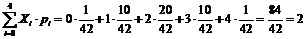 .
.
Дисперсию случайной величины найдем по формуле
D (X)= M (X2) – (M (X))2.
В результате получим
D (X)= 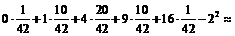 0,667,
0,667,
а среднее квадратическое отклонение соответственно равно:
s(X)= 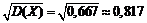 .
.
Вероятность нормально распределенной случайной величины.
Известно, что масса клубня картофеля определенного сорта является нормально распределенной случайной величиной с математическим ожиданием 110 г и средним квадратическим отклонением 30 г. Клубень считается стандартным, если он не поврежден и имеет массу в пределах 90 – 150 г. Определить:
1) процент стандартного картофеля в урожае, если повреждено 10 % клубней;
2) величину, которую не превзойдет масса отдельного клубня с вероятностью 0,95.
1. Обозначим: 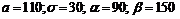 . Воспользуемся формулой попадания нормально распределенной случайной величины в заданный интервал:
. Воспользуемся формулой попадания нормально распределенной случайной величины в заданный интервал: 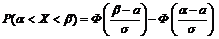 .
.
Подставив данные, получим: 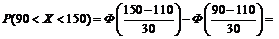
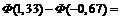
= 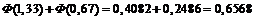 .
.
Учитывая, что 90 % клубней не повреждено, получим процент стандартного картофеля в урожае: 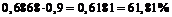 .
.
2. Обозначим: 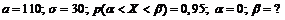
Применим предыдущую формулу:
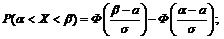
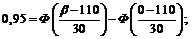
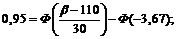
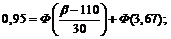
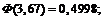
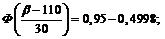
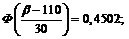
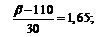
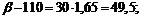
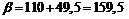 г.
г.
Таким образом, с вероятностью 0,95 можно утверждать, что масса отдельного клубня картофеля не превзойдет 159,5 г.
Задание 15
Задачи 281–300.
281.Техническое устройство содержит три независимо работающих элемента. Вероятности отказа этих элементов соответственно равны 0,05; 0,07; 0,09. Найти вероятность того, что два из них будут работать.
282. Отдел технического контроля проверяет изделия на стандартность. Вероятность того, что наугад взятое изделие окажется бракованным, равна 0,15. Проверено три изделия. Какова вероятность того, что два из них бракованные?
283. Вероятности того, что нужные сведения по мелиорации находятся в трех справочниках, соответственно равны 0,7; 0,6; 0,9. Найти вероятность того, что нужные сведения содержатся хотя бы в одном справочнике.
284. Три стрелка независимо друг от друга стреляют по цели. Вероятность попадания в цель для первого, второго и третьего стрелков равна соответственно 0,2; 0,5; 0,6. Найти вероятность того, что два стрелка попадут в цель.
285. Вероятность того, что изготовленная деталь на первом станке будет стандартная, равна 0,7; на втором – 0,8, на третьем – 0,9. От каждого станка выбирают по одной детали. Найти вероятность того, что хотя бы одна деталь будет стандартной.
286. Студент знает 15 из 20 вопросов программы. Какова вероятность того, что он знает все три вопроса, предложенные экзаменатором?
287. Для поражения цели достаточно одного поражения. По цели произведено три выстрела с вероятностями попадания 0,75; 0,85; 0,9 соответственно. Найти вероятность того, что цель будет поражена.
288. Всхожесть семян некоторой культуры составляет 90 %. В некотором опыте посажено три зерна этой культуры. Какова вероятность того, что только одно зерно даст всходы.
289. Вероятности того, что нужная деталь находится в первом, во втором, третьем ящике, соответственно равны 0,6; 0,7; 0,9. Найти вероятность того, что нужная деталь содержится в двух ящиках.
290. В поле работают три комбайна. Вероятность поломки в течение дня для первого комбайна равна 0,1, второго – 0,15, третьего – 0,2. Найти вероятность того, что в течение дня сломаются два комбайна.
291. Из партии изделий отбирают изделия высшего сорта. Вероятность того, что случайно взятые изделия имеют высший сорт, равна 0,7. Найти вероятность того, что из двух проверенных изделий хотя бы одно будет высшего сорта.
292. На ферме имеются три доильных аппарата. Вероятность исправной работы первого равна 0,8, второго – 0,9, третьего – 0,75. Найти вероятность того, что только два аппарата работают исправно.
293. В двух ящиках хранятся яблоки. Вероятность, что в первом ящике яблоко поражено болезнью, равна 0,2, во втором – 0,1. Из каждого ящика берут по одному яблоку. Найти вероятность того, что только одно яблоко поражено.
294. Экзаменационный билет содержит три вопроса. Вероятность того, что студент ответит на первый и второй вопросы, равна 0,9, на третий – 0,8. Найти вероятность того, что студент сдаст экзамен, если для этого необходимо ответить по крайней мере на два вопроса билета.
295. В партии из 10 деталей 8 стандартных. Найти вероятность того, что из наудачу извлеченных двух деталей есть хотя бы одна стандартная.
296. Многолетними наблюдениями установлено, что в данном районе в июле 15 дней бывают дождливыми. Определить вероятность того, что в течение трех первых дней июля не будет дождя.
297. На животноводческом комплексе работают три насоса. Вероятность безотказной работы первого насоса равна 0,9, второго – 0,95, третьего – 0,85. Найти вероятность того, что в течение месяца двум насосам потребуется ремонт.
298. Два стрелка делают по одному выстрелу. Вероятность попадания в мишень для первого стрелка равна 0,8, для второго –0,6. Найти вероятности того, что: а) оба стрелка попадут в цель; б) только один попадет в цель.
299. В населенном пункте имеются пять водозаборных колонок. Вероятность исправной работы одной колонки в зимний период равна 95 %. Найти вероятность того, что в зимний период ни одна колонка не потребует ремонта.
300. В трех ящиках хранятся яблоки. В первом ящике 10 % пораженных болезнью яблок, во втором – 20 %, в третьем – 15 %. Из каждого ящика берут по одному яблоку. Найти вероятности событий: а) только одно яблоко поражено; б) хотя бы одно яблоко поражено.
Задание 16
Задачи 301–310. Рабочий за смену изготовляет n деталей. Вероятность того, что деталь окажется первого сорта, равна p. Какова вероятность, что деталей первого сорта будет ровно m штук?
| 301. n =300, p =0,75, m =250.
| 302. n =500, p =0,6, m =356.
|
| 303. n =625, p =0,7, m =360.
| 304. n =196, p =0,75, m =160.
|
| 305. n =220, p =0,8, m =170.
| 306. n =105, p =0,85, m =95.
|
| 307. n =160, p =0,65, m =75.
| 308. n =650, p =0,75, m =520.
|
| 309. n =410, p =0,8, m =320.
| 310. n =400, p =0,9, m =365.
|
Задачи 311–320. Дана вероятность р появления события А в каждом из независимых испытаний. Найти вероятность того, что в этих испытаниях событие А появится не менее m 1 и не более m 2 раз.
311. n =150, p =0,6, m 1 =78, m 2 =96.
312. n =100, p =0,8, m 1 =72, m 2 =84.
313. n =400, p =0,9, m 1 =345, m 2 =372.
314. n =600, p =0,4, m 1 =210, m 2 =252.
315. n =300, p =0,75, m 1 =210, m 2 =225.
316. n =625, p =0,36, m 1 =225, m 2=255.
317. n =400, p =0,5, m 1 =190, m 2 =215.
318. n =225, p =0,2, m 1 =45, m 2 =60.
319. n =300, p =0,25, m 1 =75, m 2 =90.
320. n =625, p =0,64, m 1 =400, m 2 =430.
Задание 17
Задачи 321–330. Фермером посажено k саженцев экзотической культуры. Составить закон распределения случайной величины Х – числа прижившихся саженцев, построить многоугольник распределения этой случайной величины. Вычислить математическое ожидание, дисперсию и среднее квадратическое отклонение, если вероятность того, что любой отдельно взятый саженец приживается, равна p.
Номер задачи, количество саженцев k и вероятность p приведены в таблице.
| №
|
|
|
|
|
|
|
|
|
|
|
| n
|
|
|
|
|
|
|
|
|
|
|
| p
| 0,5
| 0,5
| 0,55
| 0,55
| 0,6
| 0,6
| 0,65
| 0,65
| 0,7
| 0,75
|
Задачи 331–340. Охотник имеет при себе k патронов и стреляет в цель до первого попадания. Составить закон распределения случайной величины Х – числа израсходованных охотником патронов, построить многоугольник распределения этой случайной величины. Вычислить математическое ожидание, дисперсию и среднее квадратическое отклонение, если вероятность попадания охотником в цель при единичном выстреле равна p.
Номер задачи, количество патронов k и вероятность p приведены в таблице.
| №
|
|
|
|
|
|
|
|
|
|
|
| n
|
|
|
|
|
|
|
|
|
|
|
| p
| 0,5
| 0,5
| 0,55
| 0,55
| 0,6
| 0,6
| 0,65
| 0,65
| 0,7
| 0,75
|
Задачи 341–360. Станок изготовляет детали, фактический размер которых является случайной величиной, распределенной по нормальному закону с математическим ожиданием a (мм) и средним квадратическим отклонением s (мм). Годными считаются детали, размер которых заключен между a и b (мм). Определить: a) процент бракованных деталей; б) процент деталей, диаметр которых отклоняется от проектного на величину, не превышающую d (мм).
341. а =25; s=0,5; a=23,5; b=25,5; d=0,2.
342. а =20; s=0,5; a=18; b=20,5; d=0,4.
343. а =18; s=1; a=16; b=19; d=0,5.
344. а =30; s=1,1; a=28; b=31; d=0,6.
345. а =32; s=0,9; a=30; b=34,5; d=0,7.
346. а =27; s=0,6; a=25; b=28,5; d=0,5.
347. а =24; s=0,7; a=22; b=26; d=0,3.
348. а =29; s=0,8; a=26; b=31; d=0,6.
349. а =19; s=0,7; a=18; b=19,5; d=0,4.
350. а =21; s=0,8; a=19; b=23; d=0,7.
351. а =24; s=0,6; a=23,5; b=25,5; d=0,3.
352. а =19; s=0,7; a=18; b=20,5; d=0,2.
353. а =17; s=0,6; a=16; b=19; d=0,1.
354. а =29; s=1; a=27; b=30; d=0,5.
355. а =31; s=0,8; a=29; b=33; d=0,6.
356. а =28; s=0,3; a=25; b=29; d=0,1.
357. а =23; s=0,8; a=22; b=25; d=0,4.
358. а =28; s=0,7; a=25; b=30; d=0,5.
359. а =20; s=0,9; a=17; b=21; d=0,6.
360. а =22; s=0,4; a=20; b=23; d=0,3.
ПРИЛОЖЕНИЯ
П р и л о ж е н и е 1
Значения функции 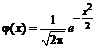
| x
|
|
|
|
|
|
|
|
|
|
|
| 0,0
| 0,3989
|
|
|
|
|
|
|
|
|
|
| 0,1
|
|
|
|
|
|
|
|
|
|
|
| 0,2
|
|
|
|
|
|
|
|
|
|
|
| 0,3
|
|
|
|
|
|
|
|
|
|
|
| 0,4
|
|
|
|
|
|
|
|
|
|
|
| 0,5
|
|
|
|
|
|
|
|
|
|
|
| 0,6
|
|
|
|
|
|
|
|
|
|
|
| 0,7
|
|
|
|
|
|
|
|
|
|
|
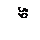 0,8 0,8
|
|
|
|
|
|
|
|
|
|
|
| 0,9
|
|
|
|
|
|
|
|
|
|
|
| 1,0
| 0,2420
|
|
|
|
|
|
|
|
|
|
| 1,1
|
|
|
|
|
|
|
|
|
|
|
| 1,2
|
|
|
|
|
|
|
|
|
|
|
| 1,3
|
|
|
|
|
|
|
|
|
|
|
| 1,4
|
|
|
|
|
|
|
|
|
|
|
| 1,5
|
|
|
|
|
|
|
|
|
|
|
| 1,6
|
|
|
|
|
|
|
|
|
|
|
| 1,7
|
|
|
|
|
|
|
|
|
|
|
П р о д о л ж е н и е п р и л. 1
| x
|
|
|
|
|
|
|
|
|
|
|
| 1,8
|
|
|
|
|
|
|
|
|
|
|
| 1,9
|
|
|
|
|
|
|
|
|
|
|
| 2,0
| 0,0540
|
|
|
|
|
|
|
|
|
|
| 2,1
|
|
|
|
|
|
|
|
|
|
|
| 2,2
|
|
|
|
|
|
|
|
|
|
|
| 2,3
|
|
|
|
|
|
|
|
|
|
|
| 2,4
|
|
|
|
|
|
|
|
|
|
|
| 2,5
|
|
|
|
|
|
|
|
|
|
|
| 2,6
|
|
|
|
|
|
|
|
|
|
|
| 2,7
|
|
|
|
|
|
|
|
|
|
|
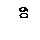 2,8 2,8
|
|
|
|
|
|
|
|
|
|
|
| 2,9
|
|
|
|
|
|
|
|
|
|
|
| 3,0
| 0,0044
|
|
|
|
|
|
|
|
|
|
| 3,1
|
|
|
|
|
|
|
|
|
|
|
| 3,2
|
|
|
|
|
|
|
|
|
|
|
| 3,3
|
|
|
|
|
|
|
|
|
|
|
| 3,4
|
|
|
|
|
|
|
|
|
|
|
| 3,5
|
|
|
|
|
|
|
|
|
|
|
| 3,6
|
|
|
|
|
|
|
|
|
|
|
| 3,7
|
|
|
|
|
|
|
|
|
|
|
| 3,8
|
|
|
|
|
|
|
|
|
|
|
| 3,9
|
|
|
|
|
|
|
|
|
|
|
П р и л о ж е н и е 2
Значения функции 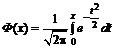
| х
| Ф(х)
| х
| Ф(х)
| х
| Ф(х)
| х
| Ф(х)
|
| 0,00
| 0,0000
| 0,39
| 0,1517
| 0,78
| 0,2823
| 1,17
| 0,3790
|
| 0,01
| 0,0040
| 0,40
| 0,1554
| 0,79
| 0,2852
| 1,18
| 0,3810
|
| 0,02
| 0,0080
| 0,41
| 0,1591
| 0,80
| 0,2881
| 1,19
| 0,3830
|
| 0,03
| 0,0120
| 0,42
| 0,1628
| 0,81
| 0,2910
| 1,20
| 0,3849
|
| 0,04
| 0,0160
| 0,43
| 0,1664
| 0,82
| 0,2939
| 1,21
| 0,3869
|
| 0,05
| 0,0199
| 0,44
| 0,1700
| 0,83
| 0,2967
| 1,22
| 0,3883
|
| 0,06
| 0,0239
| 0,45
| 0,1736
| 0,84
| 0,2995
| 1,23
| 0,3907
|
| 0,07
| 0,0279
| 0,46
| 0,1772
| 0,85
| 0,3023
| 1,24
| 0,3925
|
| 0,08
| 0,0319
| 0,47
| 0,1808
| 0,86
| 0,3051
| 1,25
| 0,3944
|
| 0,09
| 0,0359
| 0,48
| 0,1884
| 0,87
| 0,3078
| 1,26
| 0,3962
|
| 0,10
| 0,0398
| 0,49
| 0,1879
| 0,88
| 0,3106
| 1,27
| 0,3980
|
| 0,11
| 0,0438
| 0,50
| 0,1915
| 0,89
| 0,3133
| 1,28
| 0,3839
|
| 0,12
| 0,0478
| 0,51
| 0,1950
| 0,90
| 0,3159
| 1,29
| 0,4015
|
| 0,13
| 0,0517
| 0,52
| 0,1985
| 0,91
| 0,3186
| 1,30
| 0,4032
|
| 0,14
| 0,0557
| 0,53
| 0,2019
| 0,92
| 0,3212
| 1,31
| 0,4049
|
| 0,15
| 0,0596
| 0,54
| 0,2954
| 0,93
| 0,3238
| 1,32
| 0,4066
|
| 0,16
| 0,0636
| 0,55
| 0,2088
| 0,94
| 0,3264
| 1,33
| 0,4082
|
| 0,17
| 0,0675
| 0,56
| 0,2123
| 0,95
| 0,3289
| 1,34
| 0,4099
|
| 0,18
| 0,0714
| 0,57
| 0,2157
| 0,96
| 0,3315
| 1,35
| 0,4115
|
| 0,19
| 0,0753
| 0,58
| 0,2190
| 0,97
| 0,3340
| 1,36
| 0,4131
|
| 0,20
| 0,0793
| 0,59
| 0,2224
| 0,98
| 0,3365
| 1,37
| 0,4147
|
| 0,21
| 0,0832
| 0,60
| 0,2257
| 0,99
| 0,3389
| 1,38
| 0,4162
|
| 0,22
| 0,0871
| 0,61
| 0,2291
| 1,00
| 0,3413
| 1,39
| 0,4177
|
| 0,23
| 0,0910
| 0,62
| 0,2324
| 1,01
| 0,3438
| 1,40
| 0,4192
|
| 0,24
| 0,0948
| 0,63
| 0,2357
| 1,02
| 0,3461
| 1,41
| 0,4207
|
| 0,25
| 0,0987
| 0,64
| 0,2389
| 1,03
| 0,3485
| 1,42
| 0,4222
|
| 0,26
| 0,1026
| 0,65
| 0,2422
| 1,04
| 0,3508
| 1,43
| 0,4236
|
| 0,27
| 0,1064
| 0,66
| 0,2454
| 1,05
| 0,3531
| 1,44
| 0,4251
|
| 0,28
| 0,1103
| 0,67
| 0,2486
| 1,06
| 0,3554
| 1,45
| 0,4265
|
| 0,29
| 0,1141
| 0,68
| 0,2517
| 1,07
| 0,3577
| 1,46
| 0,4279
|
| 0,30
| 0,1179
| 0,69
| 0,2549
| 1,08
| 0,3599
| 1,47
| 0,4292
|
| 0,31
| 0,1217
| 0,70
| 0,2580
| 1,09
| 0,3621
| 1,48
| 0,4306
|
| 0,32
| 0,1255
| 0,71
| 0,2611
| 1,10
| 0,3643
| 1,49
| 0,4313
|
| 0,33
| 0,1293
| 0,72
| 0,2642
| 1,11
| 0,3665
| 1,50
| 0,4332
|
| 0,34
| 0,1331
| 0,73
| 0,2673
| 1,12
| 0,3686
| 1,51
| 0,4335
|
| 0,35
| 0,1368
| 0,74
| 0,2703
| 1,13
| 0,3708
| 1,52
| 0,4357
|
| 0,36
| 0,1406
| 0,75
| 0,2734
| 1,14
| 0,3729
| 1,53
| 0,4370
|
| 0,37
| 0,1443
| 0,76
| 0,2764
| 1,15
| 0,3749
| 1,54
| 0,4382
|
| 0,38
| 0,1480
| 0,77
| 0,2794
| 1,16
| 0,3770
| 1,55
| 0,4394
|
П р о д о л ж е н и е п р и л. 2
| х
| Ф(х)
| х
| Ф(х)
| х
| Ф(х)
| х
| Ф(х)
|
| 1,56
| 0,4406
| 1,82
| 0,4656
| 2,16
| 0,4846
| 2,68
| 0,4963
|
| 1,57
| 0,4418
| 1,83
| 0,4664
| 2,18
| 0,4854
| 2,70
| 0,4965
|
| 1,58
| 0,4429
| 1,84
| 0,4671
| 2,20
| 0,4861
| 2,72
| 0,4967
|
| 1,59
| 0,4441
| 1,85
| 0,4678
| 2,22
| 0,4868
| 2,74
| 0,4969
|
| 1,60
| 0,4452
| 1,86
| 0,4686
| 2,24
| 0,4875
| 2,76
| 0,4971
|
| 1,61
| 0,4463
| 1,87
| 0,4693
| 2,26
| 0,4881
| 2,78
| 0,4973
|
| 1,62
| 0,4474
| 1,88
| 0,4699
| 2,28
| 0,4887
| 2,80
| 0,4974
|
| 1,63
| 0,4484
| 1,89
| 0,4706
| 2,30
| 0,4893
| 2,82
| 0,4976
|
| 1,64
| 0,4495
| 1,90
| 0,4713
| 2,32
| 0,4898
| 2,84
| 0,4977
|
| 1,65
| 0,4505
| 1,91
| 0,4719
| 2,34
| 0,4904
| 2,86
| 0,4979
|
| 1,66
| 0,4515
| 1,92
| 0,4726
| 2,36
| 0,4909
| 2,88
| 0,4980
|
| 1,67
| 0,4525
| 1,93
| 0,4732
| 2,38
| 0,4913
| 2,90
| 0,4981
|
| 1,68
| 0,4535
| 1,94
| 0,4738
| 2,40
| 0,4918
| 2,92
| 0,4982
|
| 1,69
| 0,4545
| 1,95
| 0,4744
| 2,42
| 0,4922
| 2,94
| 0,4984
|
| 1,70
| 0,4554
| 1,96
| 0,4750
| 2,44
| 0,4927
| 2,96
| 0,4985
|
| 1,71
| 0,4564
| 1,97
| 0,4756
| 2,46
| 0,4931
| 2,98
| 0,4986
|
| 1,72
| 0,4573
| 1,98
| 0,4761
| 2,48
| 0,4934
| 3,00
| 0,49865
|
| 1,73
| 0,4582
| 1,99
| 0,4767
| 2,50
| 0,4938
| 3,20
| 0,49931
|
| 1,74
| 0,4591
| 2,00
| 0,4772
| 2,52
| 0,4941
| 3,40
| 0,49966
|
| 1,75
| 0,4599
| 2,02
| 0,4783
| 2,54
| 0,4945
< |
|
|
|



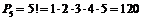 .
.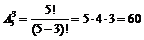 .
.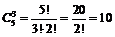 .
.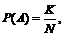
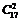 . Значит,
. Значит, 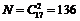 .
.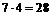 ); или одна трехтонная и одна пятитонная машины (таких способов
); или одна трехтонная и одна пятитонная машины (таких способов 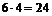 ); или две пятитонные машины (таких способов
); или две пятитонные машины (таких способов 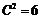 ). Итак,
). Итак, 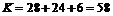 .
.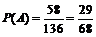 .
.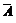 – клубень не поражен болезнью. Из условия задачи принимаем
– клубень не поражен болезнью. Из условия задачи принимаем 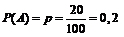 . Тогда найдем противоположного события к А
. Тогда найдем противоположного события к А 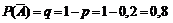 .
.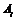 – в течение смены
– в течение смены 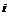 - й комбайн не потребует ремонта;
- й комбайн не потребует ремонта;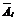 – в течение смены
– в течение смены 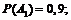
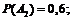
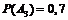 .
.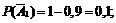
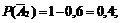
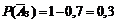 .
.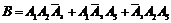 .
.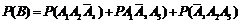 .
.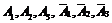 независимые, то, применяя теорему умножения вероятностей независимых событий, имеем:
независимые, то, применяя теорему умножения вероятностей независимых событий, имеем: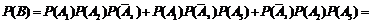 =
= 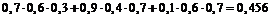 ;
;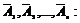
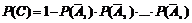 .
.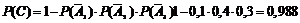 .
.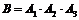 . События
. События 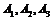 являются зависимыми, так как проходит один день и изменяется и общее количество дней, и количество недождливых дней.
являются зависимыми, так как проходит один день и изменяется и общее количество дней, и количество недождливых дней.
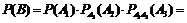
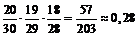 .
.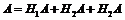 .
.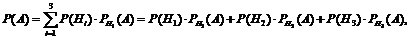
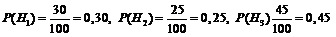 .
.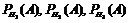 даны в условии задачи. Остается вычислить искомую вероятность:
даны в условии задачи. Остается вычислить искомую вероятность: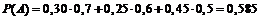 .
.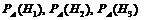 . Воспользуемся формулами Байеса, причем Р (А) мы нашли выше.
. Воспользуемся формулами Байеса, причем Р (А) мы нашли выше.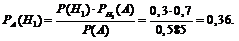
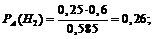
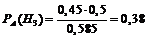 .
.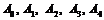
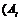 –заболеет ровно
–заболеет ровно 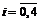 ).
).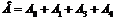 , а вероятность этого события можно найти по формуле
, а вероятность этого события можно найти по формуле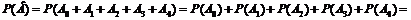
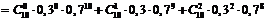
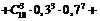
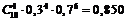 .
.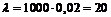 :
: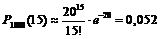 .
.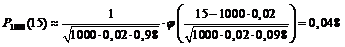 .
.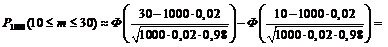 =
= 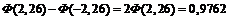 .
.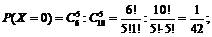
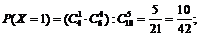
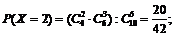
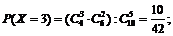
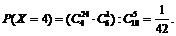
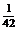
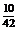
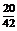
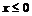 событие
событие 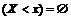 (невозможное);
(невозможное);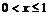 событие
событие 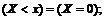
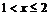 событие
событие 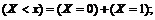
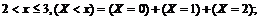
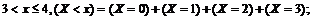
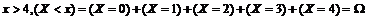 (достоверное событие).
(достоверное событие).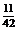
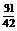
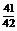
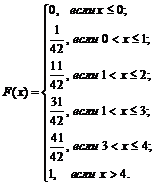
 Вероятность того, что среди отобранных будет не менее трех рекордсменок, найдем, воспользовавшись равенством
Вероятность того, что среди отобранных будет не менее трех рекордсменок, найдем, воспользовавшись равенством
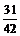 =
= 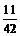 .
.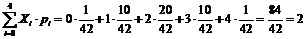 .
.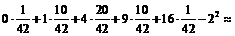 0,667,
0,667,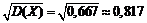 .
.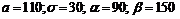 . Воспользуемся формулой попадания нормально распределенной случайной величины в заданный интервал:
. Воспользуемся формулой попадания нормально распределенной случайной величины в заданный интервал: 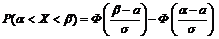 .
.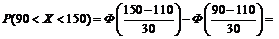
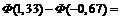
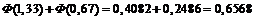 .
.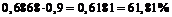 .
.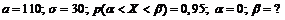
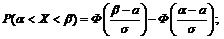
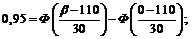
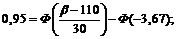
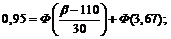
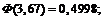
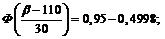
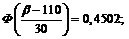
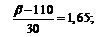
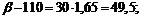
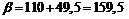 г.
г.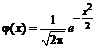
 0,8
0,8
 2,8
2,8