Каждая программа может получить доступ к ресурсам Windows, используя множество функций Программного Интерфейса Приложений (ApplicationProgrammingInterface, API).
API состоит из нескольких сотен функций, которые при необходимости могут вызваться из программы. Функции API обеспечивают доступ ко всем ресурсам Windows 95.
Запомнить функции API крайне сложно, поэтому программист должен знать способ их записи (нотацию), чтобы по имени понять назначение функции или переменной.
Нотация – это соглашение об именовании функций, переменных и констант в некоторой системе.
Имена функций Windows построены по принципу “глагол-существительное”, например: CreateWindow, LoadMenu, SendMessage.
Подробнее >>
Подмножество API, называемое Интерфейс Графических Устройств (GraphicsDeviceInterface, GDI), обеспечивает поддержку независимой от оборудования графики.
Именно функции GDI делают возможным работу Windows на весьма разнообразном оборудовании.
Итак, доступ к функциональным возможностям Windows осуществляется посредством WindowsApplicationProgrammingInterface (WinAPI).
В таблице 1.2 приведены все имеющиеся в WinAPI категории функций.
| Функции вызова стандартных диалоговых окон.
| Обеспечивают, например, выбор файла, шрифта и других часто используемых элементов такого типа.
|
| DDE-функции.
| Обеспечивают DDE-обмен (DinamicDataExchange) между приложениями.
|
| Drag&Drop-функции.
| Обеспечиваеют реализацию OLE -технологии Drag&Drop.
|
| GDI-функции.
| Эта группа включает в себя все функции графического отображения на экране линий, рамок, шрифтов.
|
| Kernel-функции.
| Базовые функции Windows (ввод/вывод, файловая система, память, подзадачи и т.д.)
|
| LZExpand- функции.
| Поддерживают сжатие/декомпрессию данных в соответствии с алгоритмом Лемпеля-Зива.
|
| OLE- функции.
| Функции этой группы поддерживают использование OLE в самом широком смысле слова. Хотя первоначально термин OLE представлял собой сокращение от ObjectLinkingandEmbedding, Microsoft предлагает и далее использовать этот термин. В настоящее время эта технология охватывает более широкую область, чем просто связывание и внедрение объектов. При выборе между DDE и OLE для передачи данных между приложениями рекомендуется отдавать предпочтение OLE, поскольку эта технология продолжает развиваться.
|
| Функции регистрации.
| Предназначены для редактирования регистрационной базы данных Windows. В ней содержится информация о приложениях системы. Эта информация используется для запуска приложений, а также при использовании технологий DDE и OLE в этих приложениях.
|
| Screensaver- функции.
| Управляют использованием Windows-заставок (ScreenSavers), а также их регистрацией и вызовом.
|
| Shell- функции.
| Позволяют расширить возможности Проводника (Explorer), напечатать файл и т.д.
|
| Stress- функции.
| Используются при распределении, присвоении и поиске блоков памяти для ресурсов с заданным дескриптором (Handle).
|
| Toolhelp- функции.
| Служат преимущественно для получения информации о различных ресурсах, используемых в Delphi 5, например о модулях и объектах.
|
| User- функции.
| Обеспечивают диалог между пользователем и системой.
|
| Version- функции.
| Служат для инсталляции и идентификации приложен
|
Вопрос №25. Свойства WINDOWS: разрядность, многозадачность, многопоточность, пользовательский интерфейс, технология PlugandPlay, поддержка длинных имен файлов, сетевые возможности.
Многие из перечисленных свойств Windows 95 являются новыми по отношению к графической оболочке Windows 3.11, представляющей собой надстройку над MSDOS. Рассмотрим их более подробно.
32-разрядность означает, что операции над 32-разрядными данными здесь выполняются заметно быстрее, чем в 16-разрядных ОС, поскольку в них требуется программная реализация над 32-разрядными данными. Под управлением Windows 95 могут выполняться н 16-разрядные приложения.
Многозадачность предоставляет возможность одновременной (параллельной) работы с несколькими приложениями. Это повышает эффективность использования микропроцессора и производительность труда пользователя.
Мпогопоточность означает способность Windows 95 организовывать одновременную обработку нескольких потоков, конкурирующих за процессорное время. При этом допускается параллельное выполнение нескольких приложений, а также нескольких фрагментов (подзадач) одного или нескольких приложений. Например, в текстовом процессоре могут одновременно выполняться автоматическая проверка орфографии и редактирование документа.
Пользовательский интерфейс Windows 95 обеспечивает удобства в запуске и переключении приложений. Основными компонентами пользовательского интерфейса являются рабочий стол (содержит ярлычки) п панель задач (обеспечивает запуск и переключение приложении). На рабочем столе размещены графические объекты, соответствующие приложениям, документам, сетевым устройствам. Каждый графический объект имеет поименованный ярлычок. С помощью мыши, ярлычков, главного меню и панели задач пользователь может легко запускать и переключать приложения.
Технология PlugandPlay (включи и работай) ориентирована на поддержку любого типа устройств, включая мониторы, видеоплаты, принтеры, звуковые карты, модемы, приводы CD-ROM, контроллеры магнитных дисков. При ее использовании обеспечиваются следующие вспомогательные функции: распознавание устройств для установки и настройки, динамическое изменение состояния системы, интеграция драйверов устройств, системных компонентов и пользовательского интерфейса. При подключении устройств Windows 95 самостоятельно выясняет используемые номера прерываний, адреса портов ввода-вывода, каналы прямого доступа к памяти. При возникновении конфликтов они разрешаются автоматически, избавляя пользователя от необходимости поиска подходящих параметров для совместно подключаемых устройств.
В Windows 95 по отношению к MSDOS для обозначения родственных понятий используется ряд новых терминов. В частности, вместо термина программа чаще используется термин приложение, который обозначает программу, выполняемую под управлением Windows. Понятие папка служит для обозначения хранилища документов и программ, структуру которых можно просмотреть с помощью проводника Windows или значка Мой компьютер. В предыдущей версии Windows и в MSDOS папки назывались каталогами.
Windows 95 содержит встроенное сетевое программное обеспечение, электронную почту (E-mail), редактор текстов WordPad, графический редактор Paint и другие вспомогательные прикладные программы. Например, программы для управления шрифтами, набора телефонного номера, воспроизведения мультимедиа, включая компакт-диски, и т.д.
3. Вопрос №26. Обмен данными между приложениями Windows. Буфер обмена. Технология OLE
4. Обмен данными между приложениями
5. Документы в Windows могут иметь сложную структуру, объединяющую тексты с графиками и различными объектами мультимедиа. Для создания и применения таких документов служит специальная технология, реализуемая системой Windows. Одним из методов такой технологии является механизм OLE (ObjectLinkingandEmbedding - Связывание и встраивание объектов). Это метод, позволяющий обеспечить интеграцию различных по своей сути объектов. Начиная с версии Windows 98, используется новая реализация этого метода, известная как OLE-2. Эта реализация делает динамический обмен данными и объектное связывание более простым и эффективным, чем ранее. В частности, обеспечивается:
6. · более естественная интеграция приложений;
7. · перемещение объектов мышкой между разными приложениями;
8. · визуальное редактирование встроенных объектов путем установки на их пиктограмму курсора мыши и выполнения «двойного клика».
9. 
10. Рис. 1. Диалоговое окно Вставка объекта
11. Для реализации этих возможностей соответствующие приложения должны иметь опцию Объект в меню Вставка. В качестве примера рассмотрим интеграцию с помощью механизма OLE-2 текстового редактора WordPad с графическим редактором Paint с целью создания текста с графическими вставками. Запустив главное приложение - текстовый редактор WordPad, наберите нужный текст и поместите курсор в то место, где вы хотите вставить рисунок. Далее выберите опцию Объект в позиции Вставка Главного меню. Вы увидите диалоговое окно, показанное на рис. 1, с запросом о том, из какого приложения ввести рисунок или в каком приложении его создать.
12. Нетрудно заметить, что диалоговое окно содержит большой список приложений, с которыми может работать WordPad. Выбрав из списка позицию Точечный рисунок, вы увидите, что окно WordPad сменится окном графического редактора, причем в окне редактирования будет видна область для создания рисунка, которую можно растягивать мышкой с ее курсором в ту или иную сторону.
13. Однако чтобы пользователь не забыл, что основным приложением является все же текстовый редактор WordPad, именно его имя стоит в титульной строке, как показано на рис. 2.
14. 
15. Рис. 2. Окно редактирования вставляемого графического объекта
16. После подготовки рисунка нужно завершить работу с графическим редактором и записать измененный и дополненный рисунком файл текстового редактора. Рисунок при этом появится на том месте, где намечалось его внедрение.
17. Если рисунок чем-то вам не понравился, подведите к нему курсор мыши и сделайте «двойной клик». Вы вновь сможете провести редактирование рисунка, используя автоматически вызываемый графический редактор.
18. Подобным образом можно выполнить импорт любого другого объекта, например данных из электронной таблицы, формул и рисунков из математических систем или задать проигрывание звуковых и видеофайлов.
19. Для загрузки файлов с диска или записи файлов после модификации на диск используются команды меню Файл. Так, команда Открыть служит для поиска загруженного файла, команда Сохранить для записи файла под текущим именем, а команда Сохранить как - для записи файла с измененным именем. Все эти команды выводят диалоговые окна, позволяющие установить нужный диск, нужный каталог и поддиректорию, задать расширение файла и т.д. Диалоговые окна у большинства приложений выполнены в едином стиле, и работа с ними не вызывает особых затруднений даже у начинающих пользователей. Для завершения работы с редактором используется команда Выход в позиции Файл Главного меню.
20. Сводка основных операций в среде Windows. При работе в графической среде большинство пользователей предпочитает мышь, однако очень полезно помнить и основные функции клавиатуры:
21. · во-первых, некоторые операции удобнее выполнять с клавиатуры (например, при переключении между окнами приложений или работе с буфером обмена);
22. · во-вторых, иногда вы можете на время отдать свою мышь или даже сломать ее;
23. · работая на клавиатуре (вводя/редактируя текст), нецелесообразно перемещать руку на мышь, значительно быстрее, если есть возможность, задать команду комбинацией клавиш.
Где находится буфер обмена и что это такое...
Эту статью я хотел бы посвятить вопросам, который волнует многих начинающих пользователей. Что такое буфер обмена?
Вы наверняка очень часто слышали в разговоре «бывалых» компьютерщиков, что они скопировали что-либо в буфер обмена, или в статьях, или в книжках были слова про эту штуку, но что это такое не объяснялось. Так что это и где находится буфер обмена, сейчас я вам и расскажу...
Сначала дам определение, которое дается во всех компьютерных словарях. Буфер обмена — промежуточное хранилище данных, предоставляемое программным обеспечением и предназначенное для переноса или копирования между приложениями или частями одного приложения. Приложение может использовать свой собственный буфер, доступный только в нём, или общий, предоставляемый операционной системой или другой средой через определённый интерфейс.
А теперь объясню своими словами.
Буфер обмена – это невидимая часть памяти, в которое временно сохраняется информация, которую вы скопировали, перед тем как вставить в нужное место. Т.е. вы выделили какой-либо файл(ы), папку(и), текст, или что-нибудь другое, нажали правой кнопкой мыши, копировать или просто нажали Ctrl+C (горячая клавиша), подробнее читайте здесь.


Они скопировались в невидимую часть памяти


Переходите в нужное место, нажимаете правой кнопкой мыши и вставить или Ctrl+V.


Вот и все. Надеюсь вы поняли где находится буфер обмена - ни где:).
Причем скопированную информацию можете вставлять много раз она храниться в этой самой невидимой части памяти, до тех пор пока вы не скопируете что-нибудь новое.
Т.е. вы скопировали папку, она сохранилась в буфер обмена, вставили её в одно место, в другое, в пятое в, десятое. А потом взяли да скопировали другую папку, так вот, первая автоматически стирается из него.
И еще в "буфе" скопированная информация хранится до тех пор, пока вы не перезагрузите или выключите компьютер. Т.е. предположим вы что-то скопировали и вас отвлекли, вы отошли от компьютера, вас не было час, два, пять, вы возвращаетесь и можете смело вставлять скопированную информацию в нужное место. Только при условии, что вы не выключали и не перезагружали комп.
OLE (англ. ObjectLinkingandEmbedding, произносится как oh-lay [олэй]) — технология связывания и внедрения объектов в другие документы и объекты, разработанная корпорацией Майкрософт.
В 1996 году Microsoft переименовала технологию в ActiveX.
OLE позволяет передавать часть работы от одной программы редактирования к другой и возвращать результаты назад. Например, установленная на персональном компьютере издательская система может послать некий текст на обработку в текстовый редактор, либо некоторое изображение в редактор изображений с помощью OLE-технологии.
Основное преимущество использования OLE (кроме уменьшения размера файла) в том, что она позволяет создать главный файл, картотеку функций, к которой обращается программа. Этот файл может оперировать данными из исходной программы, которые после обработки возвращаются в исходный документ.
OLE используется при обработке составных документов (англ. compounddocuments), может быть использована при передаче данных между различными несвязанными между собой системами посредством интерфейса переноса (англ. drag-and-drop), а также при выполнении операций с буфером обмена. Идея внедрения широко используется при работе с мультимедийным содержанием на веб-страницах (пример — Веб-ТВ), где используется передача изображения, звука, видео, анимации в страницах HTML (язык гипертекстовой разметки) либо в других файлах, также использующих текстовую разметку (например, XML и SGML). Однако, технология OLE использует архитектуру «толстого клиента», то есть сетевой ПК с избыточными вычислительными ресурсами. Это означает, что тип файла либо программа, которую пытаются внедрить, должна присутствовать на машине клиента. Например, если OLE оперирует таблицами MicrosoftExcel, то программа Excel должна быть инсталлирована на машине пользователя.
Вопрос №27. Математическая логика: история. Понятия логического выражения и логической переменной. Количество логических операций от n переменных
Здесь же вопрос №28.
Математическая логика
Математическая логика является наукой о законах математического мышления. Предметом математической логики являются математические теории в целом, которые изучаются с помощью математических языков. При этом в первую очередь интересуются вопросами непротиворечивости математических теорий, их развязности и полноты.
Математическая логика. История
Математическая логика в сущности является формальной логикой, которая использует математические методы. Формальная логика изучает акты мышления (понятия, суждения, умозаключения, доказательства) с точки зрения их формы, логической структуры, абстрагируясь от конкретного содержания. Создателем формальной логики является Аристотель, а первую завершенную систему математической логики на базе строгой логико-математического языка - алгебру логики, - предложил Джордж Буль (1815 - 1864). Логико-математические языки и теория их смысла развиты в работах Готлоб Фреге (одна тысячу восемьсот сорок-восемь - одна тысячу девятьсот двадцать-пять), который ввел понятие предикату и кванторов. Это позволило применить логико-математические языки к вопросам основ математики. Изложение целых разделов математики на языке математической логики и аксиоматизации арифметики сделаны Джузеппе Пеано (1858 - 1932). Грандиозная попытка Г. Фреге и Бертран Рассел (тысячу восемьсот семьдесят-два - 1 970) сведение всей математики к логике не достигла основной цели, но привела к созданию богатого логического аппарата, без которого оформление математической логики как полноценного раздела математики было бы невозможно.
На рубеже 19 века - 20 в. были открыты парадоксы, связанные с основными понятиями теории множеств (самым известным является парадоксы Георг Кантор и Б. Рассела). Для выхода из кризиса Л. Брауэр (тысячу восемьсот восемьдесят-одна - один тысячу девятьсот шестьдесят-шесть) выдвинул интуиционистской программу, в которой предложил отказаться от актуальной бесконечности и логического закона исключенного третьего, считая допустимыми в математике только конструктивные доказательства. Другой путь предложил Давид Гильберт (1862 - тысяча девятьсот сорок-три), который в 20-х годах 20 в. выступил с программой обоснования математики на базе математической логики. Программа Гильберта предусматривала построение формально-аксиоматических моделей (формальных систем) основным разделам математики и дальнейшее доведение их непротиворечивости надежными финитным средствами. Непротиворечивость означает невозможность одновременного вывода некоторого утверждения и его отрицания. Таким образом, математическая теория, непротиворечивость которой хотим доказать, становится предметом изучения определенной математической науки, которую Давид Гильберт назвал метаматематики, или теорией доказательств. Именно с разработки Д. Гильбертом и его учениками теории доказательств на базе развитой в работах Готлоб Фреге и Бертран Рассел логического языка начинается становление математической логики как самостоятельной математической дисциплины.
 1. Логические выражения и логические операции
1. Логические выражения и логические операции
Исследования в алгебре логики тесно связаны с изучением высказываний (хотя высказывание — предмет изучения формальной логики). Высказывание — это языковое образование, в отношении которого имеет смысл говорить о его истинности или ложности (Аристотель).
Простым высказыванием называют повествовательное предложение, относительно которого имеет смысл говорить, истинно оно или ложно.
Считается, что каждое высказывание либо истинно, либо ложно и ни одно высказывание не может быть одновременно истинным и ложным.
Примеры высказываний:
1. Москва – столица России.
2. Число 27 является простым.
3. Волга впадает в Каспийское море.
Высказывания 1 и 3 являются истинными. Высказывание 2 – ложным, потому что число 27 составное 27=3*3*3.
Следующие предложения высказываниями не являются:
- Давай пойдем гулять.
- 2*x>8.
- a*x2+b*x+c=0.
- Который час?
Итак, отличительным признаком высказывания является свойство быть истинным или ложным, последние четыре предложения этим свойством не обладают.
С помощью высказываний устанавливаются свойства, взаимосвязи между объектами. Высказывание истинно, если оно адекватно отображает эту связь, в противном случае оно ложно.
Примеры высказываний:
1. Сегодня светит солнце.
2. Трава растет.
Каждое из этих высказываний характеризует свойства или состояние конкретного объекта (в пермом предложении - погоды, во втором - окружающего мира). Каждое из этих высказываний несет значение «истина» или «ложь».
В математической логике не рассматривается конкретное содержание высказывания, важно только, истинно оно или ложно. Поэтому высказывание можно представить некоторой переменной величиной, значением которой может быть только 0 или 1. Если высказывание истинно, то его значение равно 1, если ложно - 0.
Простые высказывания назвали логическими переменными, а сложные - логическими функциями. Значения логической функции также только 0 или 1. Для простоты записи высказывания обозначаются латинскими буквами А, В, С.
Однако определение истинности высказывания далеко не простой вопрос. Например, высказывание «Число 1 +22 = 4294 967297 — простое», принадлежащее Ферма (1601-1665), долгое время считалось истинным, пока в 1732 году Эйлер (1707-1783) не доказал, что оно ложно. В целом, обоснование истинности или ложности простых высказываний решается вне алгебры логики. Например, истинность или ложность высказывания «Сумма углов треугольника равна 180°» устанавливается геометрией, причем в геометрии Евклида это высказывание является истинным, а в геометрии Лобачевского — ложным.
В булевой алгебре простым высказываниям ставятся в соответствие логические переменные, значение которых равно 1, если высказывание истинно, и 0, если высказывание ложно. Обозначаются логические переменные, большими буквами латинского алфавита.
Существуют разные варианты обозначения истинности и ложности логических переменных:
| Истина
| И
| True
| T
|
|
| Ложь
| Л
| False
| F
|
|
Сложные (составные) высказывания представляют собой набор простых высказываний (по крайней мере двух) связанных логическими операциями.
С помощью логических переменных и символов логических операций любое высказывание можно формализовать, то есть заменить логической формулой (логическим выражением).
Логическое выражение - это символическая запись высказывания, состоящая из логических величин (констант или переменных), объединенных логическими операциями (связками).
Связки "НЕ", "И", "ИЛИ" заменяются логическими операциями инверсия, конъюнкция, дизъюнкция. Это основные логические операции, при помощи которых можно записать любое логическое выражение.
Введем перечисленные логические операции.
Конъюнкция - логическое умножение (от латинскогоconjunctio - союз, связь):
- в естественном языке соответствует союзу «И»
;
- в алгебре высказываний обозначение «&»
;
- в языках программирования обозначение «And».
Конъюнкция - это логическая операция, ставящая в соответствие каждым двум простым (или исходным) высказываниям составное высказывание, являющееся истинным тогда и только тогда, когда оба исходных высказывания истинны. Если хотя бы одно из составляющих высказываний ложно, то и полученное из них с помощью союза «И» сложное высказывание также считается ложным.
В алгебре множеств конъюнкции соответствует операция пересечения множеств, т.е. множеству получившемуся в результате умножения множеств А и В соответствует множество, состоящее из элементов, принадлежащих одновременно двум множествам.
| Таблица истинности
| Диаграмма Эйлера-Венна
|
| 
|
Итак, если два высказывания соединены союзом "И", то полученное сложное высказывание истинно тогда и только тогда, когда истинны оба исходных высказывания.
Дизъюнкция - логическое сложение (от латинскогоdisjunctio - разобщение, различие):
- в естественном языке соответствует союзу «ИЛИ»
;
- в алгебре высказываний обозначение «V» или «+»
;
- в языках программирования обозначение «Or».
Дизъюнкция - это логическая операция, которая каждым двум простым (или исходным) высказываниям ставит в соответствие составное высказывание, являющееся ложным тогда и только тогда, когда оба исходных высказывания ложны и истинным, когда хотя бы одно из двух образующих его высказываний истинно.
В алгебре множеств дизъюнкции соответствует операция объединения множеств, т.е. множеству получившемуся в результате сложения множеств А и В соответствует множество, состоящее из элементов, принадлежащих либо множеству А, либо множеству В.
| Таблица истинности
| Диаграмма Эйлера-Венна
|
| 
|
Итак, если два высказывания соединены союзом "ИЛИ", то полученное сложное высказывание истинно когда истинно хотя бы одно из составляющих высказываний.
Рассмотренные выше операции были двуместными (бинарными), т.е. выполнялись над двумя операндами (высказываниями). В алгебре логики определена и широко используется и одноместная (унарная) операция отрицание.
Инверсия - отрицание (от латинскогоdisjunctio - разобщение, различие):
- в естественном языке соответствует словам «неверно, что...» и частице «не»
;
- в алгебре высказываний обозначение «» или «-»
;
- в языках программирования обозначение «Not».
Отрицание - логическая операция, которая с помощью связки «не» каждому исходному высказыванию ставит в соответствие составное высказывание, заключающееся в том, что исходное высказывание отрицается.
В алгебре множеств логическому отрицанию соответствует операция дополнения до универсального множества, т.е. множеству получившемуся в результате отрицания множества А соответствует множество, дополняющее его до универсального множества.
| Таблица истинности
| Диаграмма Эйлера-Венна
|
| 
|
Итак, если исходное выражение истинно, то результат отрицания будет ложным, и наоборот, если исходное выражение ложно, то результат отрицания будет истинным.
Логическое следование (импликация):
Высказывание, составленное из двух высказываний при помощи связки «если..., то...», называется логическим следованием, импликацией (импликация от латинскогоimplico - тесно связываю).
A => B
"Из А следует В"
Итак, новое высказывание, полученное с помощью импликации, является ложным тогда и только тогда, когда условие (посылка А) - истинно, а следствие (заключение В) - ложно и истинно во всех остальных случаях.
Пример. Дано сложное высказывание: «Если выглянет солнце, то станет тепло». Требуется записать его в виде логической формулы. Обозначим через А простое высказывание «выглянет солнце», а через В - «станет тепло». Тогда логической формулой этого сложного высказывания будет импликация: A -> B.
Эквивалентность (логическое тождество):
Высказывание, составленное из двух высказываний при помощи связки «тогда и только тогда, когда», называется эквивалентностью (эквивалентность - логическое тождество, равнозначность, взаимная обусловленность.)
A <=> B
"А равносильно В"
Итак, новое высказывание, полученное с использованием эквивалентности, является истинным тогда и только тогда, когда оба исходных высказывания одновременно истинны или одновременно ложны.
В алгебре логики логические связки и соответствующие им логические операции имеют специальные названия и обозначаются следующим образом:
| Логическая связка
| Название логической операции
| Обозначения
|
| не
| Отрицание, инверсия
| Ø, ù
|
| и, а, но
| Конъюнкция, логическое умножение
| &, •, Ù
|
| или
| Дизъюнкция, логическое сложение
| V, +
|
| если..., то
| Импликация, следование
| Þ,®
|
| тогда и только тогда, когда
| эквивалентность, эквиваленция, равнозначность
| Û, ~, º, «
|
Примеры записи сложных высказываний с помощью обозначения логических связок:
1. "Быть иль не быть - вот в чем вопрос." (В. Шекспир) А V A <=>В
2. "Если хочешь быть красивым, поступи в гусары." (К. Прутков) А =>В
ЛОГИЧЕСКИЕ ПЕРЕМЕННЫЕ [logicalvariables] — знаки и формулы, которые могут принимать различные значения в зависимости от содержания обозначаемых ими высказываний
Вопрос №29. Законы математической логики: переместительный, сочетательный, распределительный, де Моргана, идемпотенции.
Логические функции и их преобразования. Законы логики
Для операций конъюнкции, дизъюнкции и инверсии определены законы булевой алгебры, позволяющие производить тождественные (равносильные) преобразования логических выражений.
Законы логики
1. А <=> A закон двойного отрицания;
2. A&B <=> B&A коммутативность конъюнкции;
3. AVB <=> BVA коммутативность дизъюнкции;
4. A&(B&C) <=> (A&B)&C ассоциативность конъюнкции;
5. AV(BVC) <=> (AVB)VC ассоциативность дизъюнкции;
6. A&(BVC) <=> (A&B)V(A&C) дистрибутивность конъюнкции относительно дизъюнкции;
7. AV(B&C) <=> (AVB)&(AVC) дистрибутивность дизъюнкции относительно конъюнкции;
8. A&A <=> A
9. AVA <=> A
10. AVA<=> И закон исключенного третьего;
11. A&A <=> Л закон непротиворечия;
12. A&И<=> A
13.AVИ<=>И
14.A&Л<=>Л
15.AVЛ<=> A
16.(A&B) <=> A V B законыдеМоргана;
17. (AVB) <=> A & B
18. A => B <=> A V B замена импликации.
1. Законы де Моргана:
А  В =
В =  &
&  ; А&В =
; А&В = 

 .
.
Словесные формулировки законов де Моргана:
Отрицание  есть
есть  отрицаний.
отрицаний.
Отрицание истинности А  В тождественно тому, что неверно А
В тождественно тому, что неверно А 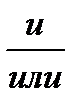 неверно В.
неверно В.
Примеры выполнения закона де Моргана:
Высказывание Неверно, что я люблю заниматься спортом и утром делать зарядку тождественно высказыванию Или я не люблю заниматься спортом или не люблю утром делать зарядку.
Высказывание Неверно, что я знаю китайский или арабский язык тождественно высказыванию Я не знаю китайского языка и не знаю арабского языка.
Вопрос №30. Законы математической логики: поглощения, склеивания, операции переменной с ее инверсией, операции переменной с константами, двойного отрицания.
Закон поглощения
А ∨ АВ ≡ А, А(А ∨ В) ≡ А
Закон склеивания
АВ ∨ А В ≡ А











 1. Логические выражения и логические операции
1. Логические выражения и логические операции


 В =
В =  &
&  ; А&В =
; А&В =  есть
есть  отрицаний.
отрицаний. В тождественно тому, что неверно А
В тождественно тому, что неверно А 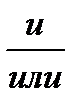 неверно В.
неверно В.

