Многомерные случайные величины

В практических задачах приходится сталкиваться со случаями, когда результат описывается двумя и более случайными величинами, образующими систему слу­чайных величин (случайный вектор). Например, точка попадания снаряда имеет две координаты: х и у, кото­рые можно принять за систему случайных величин, определенных на одном и том же пространстве элемен­тарных событий Ω.

Закон распределения дискретной двумерной случайной величины можно представить в виде таблицы, характеризу­ющей собой совокупность всех значений случайных вели­чин и соответствующих вероятностей:

	x1	x2	…	xn	Σ P(yj)
y1	P(x1,y1)	P(x2,y2)	…	P(xn,y1)	P(y1)
y2	P(x1,y2)	P(x2,y2)	…	P(xn,y2)	P(y2)
…	…	…	…	…	…
ym	P(x1,ym)	P(x2,ym)	…	P(xn,ym)	P(ym)
Σ Pxi	P(x1)	P(x2)	…	P(xn)

В общем случае двумерная случайная величина за­дается в виде интегральной функции, которая означа­ет вероятность попадания двумерной случайной вели­чины в квадрант левее и ниже точки с координатами (х, y):

F(x, у) = Р(Х<х, Y<y).

Свойства интегральной функции:

1. F - не убывает и непрерывна слева по каждому аргументу.

2. F(-∞, у)= F(x,-∞)= F(-∞, -∞)= 0.

3. F(+∞, у)= F₂(y) - функция распределения случайной величины Y. F(x,+∞)= F₁,(x) - функция распределения случайной ве­личины X.

4. F(+∞,+∞)=l.

Вероятность попадания двумерной случайной вели­чины в прямоугольник определяется исходя из опреде­ления интегральной функции двумерной случайной ве­личины (рис.17):

Р((х, у) c D) = F(β,δ) - F(α,β) - F(β,γ) + F(α,γ).

Рис. 17. Вероятность попадания точки (х, у) в прямоугольник D

Случайные величины X, Y независимы, если F(x, у) = = F₁(x)* F₂(y).

Дифференциальная функция системы двух непрерыв­ных случайных величин определяется как вторая сме­шанная производная функции распределения: f(x,y)=(∂²F(x,y))/∂x∂y=F″_xy(x,y).

Свойства дифференциальной функции:

l.f(x,y)>0;

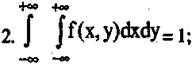
Геометрически свойство 2 означает, что объем тела, огра­ниченного поверхностью f (x, у) и плоскостью XOY, равен 1.

Если случайные величины X и Y независимы, то f(x,y) = f₁(x) f₂(y), где f₁(x)=F’₁(x),f₂(y)=F’₂(y).

В противном случае f (x, у) = f₁(x) f (y / x) или f (x, y) = f₂(y) f (x / y), где f(y/x)=f(x,y)/f₁(x) - условная дифференциальная функция CB Y при задан­ном значении X = x, f(y/x)=f(x,y)/f₂(x) - условная дифференциальная функция СВ X при заданном значении Y= у;

- дифференциальные функции отдельных случайных величин X и Y, входящих в систему.

24. Числовые характеристики системы двух слу­чайных величин. Корреляционный момент. Коэф­фициент корреляции.

Начальным моментом порядка s,h системы двух слу­чайных величин X, Y называется математическое ожи­дание произведения степени s случайной величины X и степени h случайной величины Y:

α_s,h =M(X^sY^h).

Центральным, моментом порядка s, h системы СВ (X, Y) называется математическое ожидание произведения степеней s, h соответствующих центрированных слу­чайных величин: μ_s,h =M(X^SY^h), где X =X-М(X),

Y=Y-М(Y)-центрированные слу­чайные величины X и Y.

Основным моментом порядка s, h системы СВ (X,Y) на­зывается нормированный центральный момент порядка s, h:

Начальные моменты α_1.0, α_0,1

α_1.0=M(X¹Y⁰)=M(X); α_0.1=M(X⁰Y¹)=M(Y).

Вторые центральные моменты: μ_2,0=M(X²Y⁰)=M(x-M(X))²=D(X) - характеризует рассеяние случайных величин в направлении оси ОХ.

μ_2,0 = M(X⁰Y²) = M(y-M(Y))² = D(Y) - характеризу­ет рассеяние случайных величин в направлении оси OY.

Особую роль в качестве характеристики совместной вариации случайных величин X и Y играет второй сме­шанный центральный момент, который называется кор­реляционным моментом - K(X,Y) или ковариацией -cov(X,Y): μ_1,1=K(X,Y)=cov(X,Y)=M(X¹Y¹)=M(XY)-M(X)M(Y).

Корреляционный момент является мерой связи случай­ных величин.

Если случайные величины X и Y независимы, то матема­тическое ожидание равно произведению их математических ожиданий: М (XY)= М (X) М (Y), отсюда cov(X,Y)=0.

Если ковариация случайных величин не равна нулю, то го­ворят, что случайные величины коррелированны. Ковариация может принимать значения на всей числовой оси, поэтому в качестве меры связи используют основной момент порядка s=1, h=1,который называют коэффициентом корреляции:

Свойства коэффициента корреляции:

1. -1<r_ху<1.

2. Если r = +1, то случайные величины линейно зависимы;

3. Если r_ху = 0, то случайные величины некоррелиро­ванны, что не означает их независимости вообще.

Замечание. Если случайные величины X и Y подчиня­ются нормальному закону распределения, то некоррелиро­ванность СВ X и Y означает их независимость.