Экзаменационные билеты по высшей математике
Понятие производной, её геометрический смысл. Уравнения касательной и нормали к графику функции.
 1.Производной функции f(x) (f'(x0)) в точке x0 называется число, к которому стремится разностное отношение
1.Производной функции f(x) (f'(x0)) в точке x0 называется число, к которому стремится разностное отношение  , стремящееся к нулю.
, стремящееся к нулю.
 - Производная функции, заданной на некотором интервале (a;b), в некоторой точке Х этого интервала называют предел отношения приращения функции к приращению аргумента.
- Производная функции, заданной на некотором интервале (a;b), в некоторой точке Х этого интервала называют предел отношения приращения функции к приращению аргумента.







 2.Геометрический смысл производной.
2.Геометрический смысл производной.
Производная в точке x0 равна угловому коэффициенту касательной к графику функции y=f(x) в этой точке.
Касательная к графику- предельное положение секущей.



3.Уравнение касательной к графику функции y=f(x) в точке x0:
 Касательная — это прямая, которая касается графика функции в одной точке и все точки которой находятся на наименьшем расстоянии от этого графика функции, уравнение касательной запишется таким образом.
Касательная — это прямая, которая касается графика функции в одной точке и все точки которой находятся на наименьшем расстоянии от этого графика функции, уравнение касательной запишется таким образом.
 4. Уравнение нормали графика
4. Уравнение нормали графика
Нормаль – это перпендикулярная к касательной прямая, проходящая через точку касания
Физический смысл производной. Скорость материальной точки при непрерывном движении.
Физический смысл производной- Скорость в определённый момент времени – это производная координаты по времени.
 Так как на малом участке пути ΔS скорость меняется незначительно,то допустим, что она постоянна=>.
Так как на малом участке пути ΔS скорость меняется незначительно,то допустим, что она постоянна=>.
Мгновенная cкорость материальной точки.
При времени t.
Левая и правая производные(односторонние). Дифференцируемость.

 Левой и правой производной функции в точке х0, называется правое(левое) предельное значение.
Левой и правой производной функции в точке х0, называется правое(левое) предельное значение.
При условии, что оно существует.
Если функция в точке х0 имеет производную, то она в этой точке имеет левую и правую производные, совпадающие между собой.
 Так же есть функция, которая имеет правую и левую производные, но не имеет производную точки.
Так же есть функция, которая имеет правую и левую производные, но не имеет производную точки.
Например. f(x)= |х|: в точке х=0

 правая
правая
левая
Но не имеет в точке х=0 производной, т.к односторонние пределы различны.
Дифференцируемость
Теорема. Если функция в точке имеет производную, то она непрерывна в этой точке.
=> 
 =>
=> 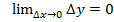 => функция непрерывна
=> функция непрерывна
Функция дифференцированная если у неё существует производная.
дифференцируемость => непрерывность (обратное утверждение не верно)
Функция гладкая, если производная есть на всей области определения.

 50. Таблица производных. Свойства производных.
50. Таблица производных. Свойства производных.
Доказательство свойств:
 1.
1.
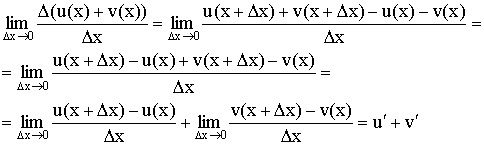 2.
2.


3.
 4.
4.
Свойства дифференцируемых функций. Теоремы Ролля, Коши, Лангранджа.
 Теорема №1 (Ролль)
Теорема №1 (Ролль)
Пусть функция f(x) непрерывна на отрезке [ a;b ], дифференцируема на интервале (a;b) и на концах принимает равные значения (f(a)=f(b)), тогда существует точка c∈(a;b), в которой производная функции равна 0 (f’(c)=0).
Доказательство.
По т. Вейерштрасса (Если функция f(x) непрерывна на отрезке [a,b], то она достигает на нем своей точной верхней и нижней грани (т.е. наибольшего и наименьшего значения).)

Если m=M, то f(x)=const, тогда f’(x)=0.
Пусть m≠M, хотя бы одно из значений внутри отрезка ∃ c ∈(a;b); f(c)=M
В силу теоремы верно неравенство f(c+∆x)-f(c) = 0, а ∆x→0, то

Теорема №2 (Коши)
 Пусть функции f (x) и g(x) непрерывны на [a; b] и дифференцируемы на (a; b). Пусть, кроме того, во всех точках интервала (a; b) функция g(x) имеет ненулевую производную g ' (x) ≠ 0. Тогда существует точка c ∈ (a; b), такая, что справедлива формула.
Пусть функции f (x) и g(x) непрерывны на [a; b] и дифференцируемы на (a; b). Пусть, кроме того, во всех точках интервала (a; b) функция g(x) имеет ненулевую производную g ' (x) ≠ 0. Тогда существует точка c ∈ (a; b), такая, что справедлива формула.
Отношение приращений 2 функций на отрезке равно отношению значений их производных.

Доказательство.

F(a)=0; F(b)=0 => удовлетворяет т.Ролля.
∃ с ∈(a;b) F'(c)=0
 /
/
/
Теорема №3 (Лагранж)
 Пусть функция f(x) непрерывна на отрезке [ a;b ], дифференцируема на интервале (a;b) и на концах принимает равные значения (f(a)=f(b)), то найдётся хотя бы точка c∈(a;b) такая, что выполняет равенство:
Пусть функция f(x) непрерывна на отрезке [ a;b ], дифференцируема на интервале (a;b) и на концах принимает равные значения (f(a)=f(b)), то найдётся хотя бы точка c∈(a;b) такая, что выполняет равенство:
Доказательство. применим т.Коши
(f(b) - f(a))’=f’(c), a (b-a)’=1 



 53. Раскрытие неопределённостей. Правило Лопиталя.
53. Раскрытие неопределённостей. Правило Лопиталя.

- неопределённости.
 Можно применять неоднократно.
Можно применять неоднократно.
Для раскрытия неопределенностей надо заменить предел отношения двух функций пределом отношения их производных. Если окажется, что отношение производных имеет конечный предел, то к этому же пределу стремится и отношение данных функций.


 54. Признаки монотонности функции.
54. Признаки монотонности функции.


Строго монотонная -когда постоянно воз(убыв),
Монотонная -когда не постоянно воз(убыв).
Доказательство.

Экзаменационные билеты по высшей математике



 1.Производной функции f(x) (f'(x0)) в точке x0 называется число, к которому стремится разностное отношение
1.Производной функции f(x) (f'(x0)) в точке x0 называется число, к которому стремится разностное отношение  , стремящееся к нулю.
, стремящееся к нулю.




 2.Геометрический смысл производной.
2.Геометрический смысл производной. Касательная — это прямая, которая касается графика функции в одной точке и все точки которой находятся на наименьшем расстоянии от этого графика функции, уравнение касательной запишется таким образом.
Касательная — это прямая, которая касается графика функции в одной точке и все точки которой находятся на наименьшем расстоянии от этого графика функции, уравнение касательной запишется таким образом. 4. Уравнение нормали графика
4. Уравнение нормали графика Так как на малом участке пути ΔS скорость меняется незначительно,то допустим, что она постоянна=>.
Так как на малом участке пути ΔS скорость меняется незначительно,то допустим, что она постоянна=>.

 =>
=> 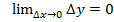 => функция непрерывна
=> функция непрерывна
 50. Таблица производных. Свойства производных.
50. Таблица производных. Свойства производных. 1.
1.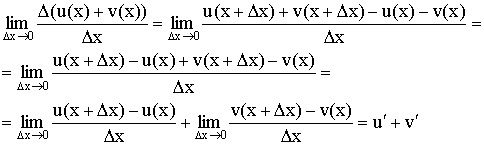 2.
2.

 4.
4. Теорема №1 (Ролль)
Теорема №1 (Ролль)

 Пусть функции f (x) и g(x) непрерывны на [a; b] и дифференцируемы на (a; b). Пусть, кроме того, во всех точках интервала (a; b) функция g(x) имеет ненулевую производную g ' (x) ≠ 0. Тогда существует точка c ∈ (a; b), такая, что справедлива формула.
Пусть функции f (x) и g(x) непрерывны на [a; b] и дифференцируемы на (a; b). Пусть, кроме того, во всех точках интервала (a; b) функция g(x) имеет ненулевую производную g ' (x) ≠ 0. Тогда существует точка c ∈ (a; b), такая, что справедлива формула.

 /
/ Пусть функция f(x) непрерывна на отрезке [ a;b ], дифференцируема на интервале (a;b) и на концах принимает равные значения (f(a)=f(b)), то найдётся хотя бы точка c∈(a;b) такая, что выполняет равенство:
Пусть функция f(x) непрерывна на отрезке [ a;b ], дифференцируема на интервале (a;b) и на концах принимает равные значения (f(a)=f(b)), то найдётся хотя бы точка c∈(a;b) такая, что выполняет равенство:



 53. Раскрытие неопределённостей. Правило Лопиталя.
53. Раскрытие неопределённостей. Правило Лопиталя.
 Можно применять неоднократно.
Можно применять неоднократно.
 54. Признаки монотонности функции.
54. Признаки монотонности функции.



