Рассмотрим случай, когда имеется возможность заимствования денежных средств. Инвестор не ограничен своим начальным капиталом при принятии решения о том, сколько денег инвестировать в рисковые активы. Но, если инвестор занимает деньги, он должен платить процент по займу. Если процентная ставка известна и неопределенность с выплатой займа отсутствует, то это часто называется безрисковым заимствованием.
Сначала предположим, что процентная ставка по займу равна ставке, которая может быть заработана инвестированием в безрисковые активы. Это означает, что инвестор имеет возможность не только инвестировать в безрисковый актив под процентную ставку 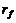 , но также он может получить заем, за который обязан платить процентную ставку, равную
, но также он может получить заем, за который обязан платить процентную ставку, равную 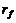 .
.
Прежде считалось, что доля, инвестированная в безрисковый актив, является положительным числом от 0 до 1. Так как теперь имеется возможность получать заем по той же процентной ставке, эти ограничения снимаются, так как в случае займа доля безрискового актива будет отрицательной.
Пусть портфель инвестора с капиталом, равным 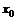 , составлен из рисковых ценных бумаг в количествах
, составлен из рисковых ценных бумаг в количествах 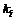 со стоимостями
со стоимостями 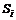 ,
, 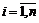 . Тогда бюджетное ограничение при наличии безрискового заимствования средств размером В будет иметь вид
. Тогда бюджетное ограничение при наличии безрискового заимствования средств размером В будет иметь вид
 ,
,
Причем
 ,
,
где 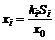 ,
, 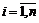 - доли ценных бумаг в портфеле,
- доли ценных бумаг в портфеле, 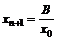 - доля заимствованных средств.
- доля заимствованных средств.
Покажем, как меняется эффективное множество, если введена возможность как предоставления, так и получения займа по одной и той же безрисковой процентной ставке. Как и в случае безрискового кредитования, портфели, являющиеся комбинацией безрискового актива и рискового портфеля А, лежат на прямой  (рис.2.5.1). Оптимальные портфели в случае безрискового заимствования будут лежать на продолжении прямой
(рис.2.5.1). Оптимальные портфели в случае безрискового заимствования будут лежать на продолжении прямой  вправо-вверх. Кроме «касательного» портфеля М ни один из портфелей, которые находились в эффективном множестве модели Марковица, не является эффективным после введения возможности предоставления и получения займа. Это следует из того, что для любого портфеля, принадлежащего эффективному множеству Марковица, найдется альтернативный портфель, лежащий на верхнем луче (рис.2.5.1.), с большей ожидаемой доходностью при том же самом среднеквадратическом отклонении.
вправо-вверх. Кроме «касательного» портфеля М ни один из портфелей, которые находились в эффективном множестве модели Марковица, не является эффективным после введения возможности предоставления и получения займа. Это следует из того, что для любого портфеля, принадлежащего эффективному множеству Марковица, найдется альтернативный портфель, лежащий на верхнем луче (рис.2.5.1.), с большей ожидаемой доходностью при том же самом среднеквадратическом отклонении.

Рис. 2.5.1. Эффективное множество в случае возможности безрискового заимствования и кредитования
Пример 2.5.1. На формирование рискового портфеля с математическим ожиданием 18% заимствовано 20% средств. Определить состав данного портфеля и его дисперсию, если даны вектор ожидаемых доходностей и матрица ковариаций
М= 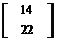 ,
, 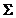 =
=  .
.
Безрисковая ставка равна 5%.
Решение. Пусть  искомый портфель. Справедливо равенство
искомый портфель. Справедливо равенство
 .
.
Математическое ожидание доходности портфеля и дисперсия определяются формулами
 ,
,
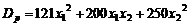 .
.
Решением системы

будут  ,
,  . Теперь вычисляем дисперсию портфеля
. Теперь вычисляем дисперсию портфеля
 .
.
Имеем портфель  с дисперсией 173,3.
с дисперсией 173,3.
Теперь посмотрим, как изменится эффективное множество, если инвестор получает займ по ставке, превышающей доходность от инвестирования в безрисковый актив.
Обозначим через 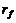 ставку по безрисковому активу, через
ставку по безрисковому активу, через 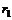 ставку, по которой инвестор может получить заем. Заметим, что
ставку, по которой инвестор может получить заем. Заметим, что  .
.
Если получение и предоставление займа возможно по одной и той же ставке, то результирующее эффективное множество является прямой линией, проходящей через 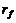 и
и 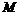 (рис. 2.5.2). Если величину ставки увеличить до
(рис. 2.5.2). Если величину ставки увеличить до 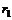 , то результирующее эффективное множество будет прямой линией, проходящей через
, то результирующее эффективное множество будет прямой линией, проходящей через 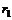 и
и  . Причем
. Причем  расположена на эффективном множестве выше
расположена на эффективном множестве выше 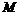 . Если инвестор не может получить заем по ставке
. Если инвестор не может получить заем по ставке 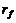 , то часть линии, которая продолжается правее
, то часть линии, которая продолжается правее 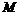 , недоступна и поэтому далее не рассматривается. Если инвестор не может предоставить кредит по ставке
, недоступна и поэтому далее не рассматривается. Если инвестор не может предоставить кредит по ставке 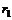 , то часть линии, которая лежит левее
, то часть линии, которая лежит левее  , также не рассматривается.
, также не рассматривается.
В результате, эффективное множество будет состоять из трех различных частей (рис.2.5.2). Первой частью является отрезок, соединяющий 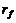 и
и 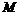 , который представляет собой различные комбинации безрисковых активов в сочетание с инвестированием в портфель рискового актива М. Второй частью является участок кривой из эффективного множества Марковица, соединяющий точки
, который представляет собой различные комбинации безрисковых активов в сочетание с инвестированием в портфель рискового актива М. Второй частью является участок кривой из эффективного множества Марковица, соединяющий точки 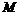 и
и  . Третьей частью является луч, выходящий из точки
. Третьей частью является луч, выходящий из точки  (это точка касания прямой, проходящей через
(это точка касания прямой, проходящей через 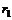 ), которая представляет собой различные комбинации заимствования в сочетании с инвестированием в рисковой портфель
), которая представляет собой различные комбинации заимствования в сочетании с инвестированием в рисковой портфель  .
.

Рис.2.5.2. Эффективное множество при неравных безрисковых ставках
Упражнения
1. Инвестор владеет рисковым портфелем, имеющим 25%-ное стандартное отклонение. Если на формирование данного портфеля было заимствовано 30% средств, то чему равно стандартное отклонение этого портфеля, если даны вектор ожидаемых доходностей и матрица ковариаций
М=  ,
, 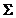 =
=  .
.
Безрисковая ставка равна 6%.
2. Портфель, состоящий из обыкновенных акций, имеет 20%-ную ожидаемую доходность. Какова ожидаемая доходность портфеля, если его владелец инвестирует 110% своих средств в рисковый портфель? Безрисковая ставка равна 6%.
3. На рынке имеются два вида акций, доходности которых независимы и равномерно распределены на интервалах (0,1; 0,3) и (0,15; 0,2). Инвестор для их покупки заимствовал 20% средств. Определить среднеквадратическое отклонение доходности, если безрисковый процент и ожидаемое значение доходности полученного портфеля равны соответственно
а) 8% и 0,2;
б) 5% и 0,22.
4. В портфеле инвестора акций А в два раза меньше акций В и в пять раз меньше акций С. На его формирование он занял 30% своего капитала под 4% годовых. Определить состав данного портфеля и его среднюю доходность, если дан вектор ожидаемых доходностей
М=  .
.
§2.6. Модель ценообразования финансовых активов
Данная теория известна как САРМ. В ней изучаются свойства случайной процентной ставки некоторого финансового актива А по отношению к “глобальной” процентной ставке большого рынка. Модель оценки финансовых активов САРМ (Capital Asset Pricing Model) была впервые сформулирована Уильямом Шарпом в 1964 году, а также независимо от него Джоном Линтнером и Жаном Моссэном.
Предполагается, что активы можно размещать в банке, дающем процентную ставку  , которая обычно меньше, чем ожидаемое значение рисковых процентных ставок, отображаемое в процентная ставка большого рынка
, которая обычно меньше, чем ожидаемое значение рисковых процентных ставок, отображаемое в процентная ставка большого рынка  . Случайная процентная ставка актива А обозначим
. Случайная процентная ставка актива А обозначим  , тогда можно определить коэффициент пропорциональности
, тогда можно определить коэффициент пропорциональности  из уравнения
из уравнения 
 .
.
В рамках теории САРМ устанавливается, что этот же коэффициент  является оптимальным при оценивании центрированных значений
является оптимальным при оценивании центрированных значений  по центрированным значениям
по центрированным значениям  . Другими словами, случайные величины
. Другими словами, случайные величины  и
и  связаны уравнением
связаны уравнением
 , (2.6.1)
, (2.6.1)
где случайная величина  некоррелирована с
некоррелирована с  . Следствием последней формулы является уравнение
. Следствием последней формулы является уравнение
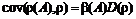 .
.
Таким образом, бетой актива называется величина
 . (2.6.2)
. (2.6.2)
С другой стороны эту же величину можно выразить так:
 . (2.6.3)
. (2.6.3)
Теория САРМ и ее выводы применимы лишь к равновесному рынку, в модели которого предполагается, что участники имеют равный доступ к информации и их решения основываются на средних значениях и ковариациях цен.
В обеих формулах (2.6.2) и (2.6.3) значение  выступает как коэффициент пропорциональности между глобальными ценами рынка и ценами актива А. В формуле (2.6.2) этот коэффициент связывает средние премии за риск по отношению к безрисковому вложению в банк, в (2.6.3) – случайное отклонение от средних значений.
выступает как коэффициент пропорциональности между глобальными ценами рынка и ценами актива А. В формуле (2.6.2) этот коэффициент связывает средние премии за риск по отношению к безрисковому вложению в банк, в (2.6.3) – случайное отклонение от средних значений.
Одним словом, величина  есть “мера чувствительности” актива А к изменениям на рынке.
есть “мера чувствительности” актива А к изменениям на рынке.
Из уравнения (2.6.1) следует, что
 .
.
Первое слагаемое характеризует систематический риск, оно определяется состоянием рынка в целом  и влиянием рынка на данный актив
и влиянием рынка на данный актив  . Второе слагаемое
. Второе слагаемое  характеризует несистематический риск, связанный с колебаниями цен конкретного актива.
характеризует несистематический риск, связанный с колебаниями цен конкретного актива.
При выборе портфеля ценных бумаг невозможно подавить систематический риск иначе, чем подбором активов, некоррелированных с глобальным рынком, то есть с малыми значениями  . Несистематический риск можно подавить диверсификацией.
. Несистематический риск можно подавить диверсификацией.
График линейной функции  от аргумента
от аргумента  называют также “прямая САРМ”.
называют также “прямая САРМ”.



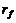 , но также он может получить заем, за который обязан платить процентную ставку, равную
, но также он может получить заем, за который обязан платить процентную ставку, равную 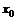 , составлен из рисковых ценных бумаг в количествах
, составлен из рисковых ценных бумаг в количествах 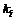 со стоимостями
со стоимостями 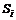 ,
, 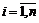 . Тогда бюджетное ограничение при наличии безрискового заимствования средств размером В будет иметь вид
. Тогда бюджетное ограничение при наличии безрискового заимствования средств размером В будет иметь вид ,
, ,
,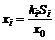 ,
, 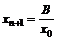 - доля заимствованных средств.
- доля заимствованных средств. (рис.2.5.1). Оптимальные портфели в случае безрискового заимствования будут лежать на продолжении прямой
(рис.2.5.1). Оптимальные портфели в случае безрискового заимствования будут лежать на продолжении прямой 
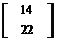 ,
,  =
=  .
. искомый портфель. Справедливо равенство
искомый портфель. Справедливо равенство .
. ,
,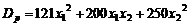 .
.
 ,
,  . Теперь вычисляем дисперсию портфеля
. Теперь вычисляем дисперсию портфеля .
. с дисперсией 173,3.
с дисперсией 173,3. ставку, по которой инвестор может получить заем. Заметим, что
ставку, по которой инвестор может получить заем. Заметим, что  .
.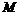 (рис. 2.5.2). Если величину ставки увеличить до
(рис. 2.5.2). Если величину ставки увеличить до  . Причем
. Причем 
 ,
,  .
. .
. , которая обычно меньше, чем ожидаемое значение рисковых процентных ставок, отображаемое в процентная ставка большого рынка
, которая обычно меньше, чем ожидаемое значение рисковых процентных ставок, отображаемое в процентная ставка большого рынка  . Случайная процентная ставка актива А обозначим
. Случайная процентная ставка актива А обозначим  , тогда можно определить коэффициент пропорциональности
, тогда можно определить коэффициент пропорциональности 
 .
. является оптимальным при оценивании центрированных значений
является оптимальным при оценивании центрированных значений  , (2.6.1)
, (2.6.1) некоррелирована с
некоррелирована с 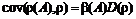 .
. . (2.6.2)
. (2.6.2) . (2.6.3)
. (2.6.3) .
. и влиянием рынка на данный актив
и влиянием рынка на данный актив  . Второе слагаемое
. Второе слагаемое  характеризует несистематический риск, связанный с колебаниями цен конкретного актива.
характеризует несистематический риск, связанный с колебаниями цен конкретного актива. . Несистематический риск можно подавить диверсификацией.
. Несистематический риск можно подавить диверсификацией. от аргумента
от аргумента 


