

Типы оградительных сооружений в морском порту: По расположению оградительных сооружений в плане различают волноломы, обе оконечности...

Семя – орган полового размножения и расселения растений: наружи у семян имеется плотный покров – кожура...

Типы оградительных сооружений в морском порту: По расположению оградительных сооружений в плане различают волноломы, обе оконечности...

Семя – орган полового размножения и расселения растений: наружи у семян имеется плотный покров – кожура...
Топ:
Определение места расположения распределительного центра: Фирма реализует продукцию на рынках сбыта и имеет постоянных поставщиков в разных регионах. Увеличение объема продаж...
Отражение на счетах бухгалтерского учета процесса приобретения: Процесс заготовления представляет систему экономических событий, включающих приобретение организацией у поставщиков сырья...
Эволюция кровеносной системы позвоночных животных: Биологическая эволюция – необратимый процесс исторического развития живой природы...
Интересное:
Берегоукрепление оползневых склонов: На прибрежных склонах основной причиной развития оползневых процессов является подмыв водами рек естественных склонов...
Принципы управления денежными потоками: одним из методов контроля за состоянием денежной наличности является...
Уполаживание и террасирование склонов: Если глубина оврага более 5 м необходимо устройство берм. Варианты использования оврагов для градостроительных целей...
Дисциплины:
|
из
5.00
|
Заказать работу |
|
|
|
|
Марковской цепи
Диаграммой переходов состояний марковской цепи в целом (как непрерывной, так и дискретной) является направленный (ориентированный) граф состояний, вершины которого соответствуют состояни-
ям, а ребра – переходам между этими состояниями. Каждое ребро должно быть помечено интенсивностью 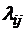 (для непрерывной марковской цепи) или вероятностью
(для непрерывной марковской цепи) или вероятностью 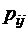 (для дискретной марковской цепи) соответствующего перехода в потоке событий. Цепь Маркова полностью определяется ее диаграммой переходов между состояниями, то есть ее графом состояний.
(для дискретной марковской цепи) соответствующего перехода в потоке событий. Цепь Маркова полностью определяется ее диаграммой переходов между состояниями, то есть ее графом состояний.
Понятие интенсивности  марковского случайного процесса вводится следующим образом. Пусть вероятность перехода из состояния i в состояние j за время от t до
марковского случайного процесса вводится следующим образом. Пусть вероятность перехода из состояния i в состояние j за время от t до 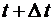 есть
есть
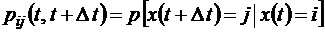 ,
,
согласно формуле (1.1.1). Тогда по определению
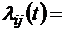 lim
lim 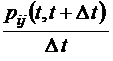
при 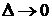 . Для так называемых однородных марковских процессов вероятности переходов не зависят от времени, так что
. Для так называемых однородных марковских процессов вероятности переходов не зависят от времени, так что 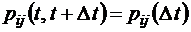 , и тогда
, и тогда 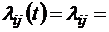 const. Для систем массового обслуживания понятие состояния определяется, как правило, общим числом заявок или требований, находящихся в системе (как в очередях, так и на обслуживании).
const. Для систем массового обслуживания понятие состояния определяется, как правило, общим числом заявок или требований, находящихся в системе (как в очередях, так и на обслуживании).
Исчерпывающей количественной характеристикой марковского процесса является совокупность вероятностей состояний системы, то есть вероятностей 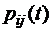 того, что в момент времени t процесс будет находиться в состоянии j (j = 0, 1, 2, …). Таким образом, наша задача заключается в том, чтобы научиться рассчитывать
того, что в момент времени t процесс будет находиться в состоянии j (j = 0, 1, 2, …). Таким образом, наша задача заключается в том, чтобы научиться рассчитывать 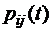 по заданным интенсивностям переходов
по заданным интенсивностям переходов 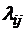 .
.
Рассмотрим, как определяются вероятности состояний по графу состояний [12], приведенному на рис. 2, считая данный случайный процесс марковским. В случайный момент времени t система может находиться в одном из пяти состояний j с вероятностями  (j = 0,
(j = 0,
|
|
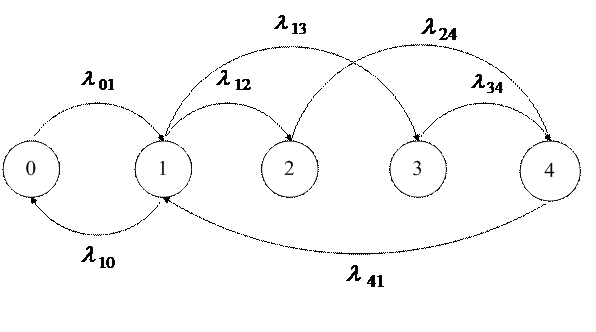
Рис. 2
1, 2, 3, 4). Придадим времени t малое приращение 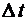 и найдем, например,
и найдем, например, 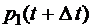 – вероятность того, что в момент времени
– вероятность того, что в момент времени 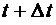 система будет находиться в состоянии 1. А это может произойти в одном из трех взаимоисключающих друг друга случаях: во-первых, если система в момент времени t была в состоянии 1 и за время
система будет находиться в состоянии 1. А это может произойти в одном из трех взаимоисключающих друг друга случаях: во-первых, если система в момент времени t была в состоянии 1 и за время 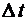 не вышла из него, а также, если в момент t система была в состояниях 0 или 4и за время
не вышла из него, а также, если в момент t система была в состояниях 0 или 4и за время 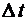 перешла в состояние 1.
перешла в состояние 1.
В этой связи напомним известный результат из курса теории вероятностей: для того чтобы найти полную вероятность какого-либо состояния j, нужно сложить вероятности всех тех событий, которые приводят к этому состоянию, точнее говоря, заканчиваются его исходом, так что
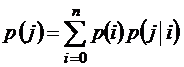
(формула полной вероятности [3; 6]). В нашем случае применение этой формулы, очевидно, будет следующим:
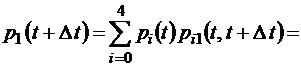 (1.2.1)
(1.2.1)
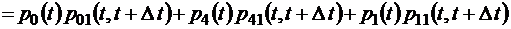 .
.
Здесь первое слагаемое означает вероятность перехода за время 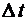 в состояние 1 из состояния 0, если в момент t система находилась в состоянии 0 с вероятностью p 0(t). Второе слагаемое означает аналогичную вероятность, но уже не для состояния 0, а для состояния 4. Последнее же третье слагаемое есть, очевидно, вероятность того, что за время
в состояние 1 из состояния 0, если в момент t система находилась в состоянии 0 с вероятностью p 0(t). Второе слагаемое означает аналогичную вероятность, но уже не для состояния 0, а для состояния 4. Последнее же третье слагаемое есть, очевидно, вероятность того, что за время 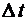 система не выйдет из состояния 1, то есть не перейдет за это время в состояния 0, 2 или 3. Вследствие этого, для того чтобы найти вероятность
система не выйдет из состояния 1, то есть не перейдет за это время в состояния 0, 2 или 3. Вследствие этого, для того чтобы найти вероятность 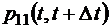 , нужно просто вычесть из единицы вероятности всех тех событий, которые выводят систему из состояния 1*. Вероятность же того, что за время
, нужно просто вычесть из единицы вероятности всех тех событий, которые выводят систему из состояния 1*. Вероятность же того, что за время 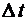 система выйдет из состояния 1, в данном случае есть, очевидно, p 10 + p 12 + p 13, то есть
система выйдет из состояния 1, в данном случае есть, очевидно, p 10 + p 12 + p 13, то есть
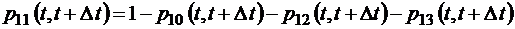 ,
,
и тогда
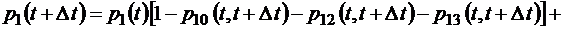
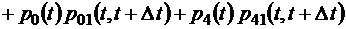 .
.
Раскроем теперь квадратные скобки в правой части этого соотношения, перенесем p1(t) в левую часть и разделим обе части на время 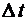 . Получим
. Получим
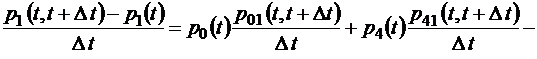
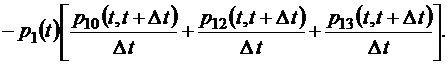
Если теперь устремить время 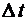 к нулю, то слева получим производную функции p 1(t), а справа – интенсивности марковского процесса λij (t):
к нулю, то слева получим производную функции p 1(t), а справа – интенсивности марковского процесса λij (t):
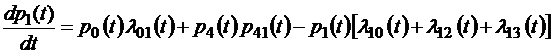 .
.
Аналогичные уравнения можно вывести и для всех остальных состояний системы, так что в итоге мы получим следующую систему квазилинейных дифференциальных уравнений для безусловных вероятностей pi (t):
|
|
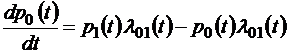 ;
;
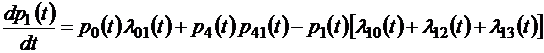 ;
;
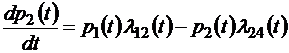 ;
;
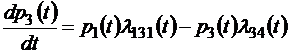 ;
;
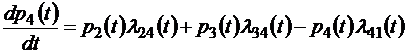 .
.
Эта система уравнений дает возможность найти вероятности pj (t) состояний системы, если заданы их начальные условия pj (0).
В левой части каждого из этих уравнений стоит производная вероятности j -го состояния системы, в правой части – сумма произведений вероятностей тех состояний, из которых ведут стрелки в j -е состояние, на интенсивности соответствующих переходов (соответствующих случайных процессов) минус суммарная интенсивность всех процессов, выводящих систему из j -го состояния, умноженная на вероятность этого состояния. В общем виде такую систему уравнений можно записать как систему с переменными коэффициентами
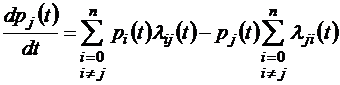 , j = 0, 1, 2, … n (1.2.2)
, j = 0, 1, 2, … n (1.2.2)
или для однородных марковских процессов как
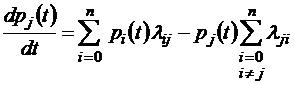 , j = 0, 1, 2, … n, (1.2.3)
, j = 0, 1, 2, … n, (1.2.3)
и в этом случае система (1.2.2) становится системой линейных дифференциальных уравнений (1.2.3).
Заметим, что в этих записях учтено то очевидное обстоятельство, что для состояний системы, не связанных непосредственными переходами друг с другом, можно считать λji = λij = 0.
Уравнения (1.2.2), (1.2.3) носят название уравнений Колмогорова и являются управляющими уравнениями для непрерывного случайного марковского процесса (непрерывной марковской цепи).
Системы дифференциальных уравнений (1.2.2), (1.2.3) решают при начальных условиях, задающих вероятности состояний системы в начальный момент времени при t = 0: p 0(0), p 1(0), … pn (0), причем для любого момента времени t должно быть выполнено условие нормировки
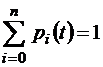 ,
, 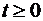 .
.
Это условие можно использовать вместо одного (и при этом любого) из дифференциальных уравнений систем (1.2.2) и (1.2.3).
При составлении уравнений Колмогорова по графу состояний системы удобно ввести понятие потока вероятности. А именно будем называть потоком вероятности, переводящим систему из состояния i в состояние j, произведение вероятности pi (t) состояния, из которого исходит стрелка на графе, на интенсивность λij (t) марковского процесса, переводящего систему по этой стрелке. Уравнения Колмогорова в этом случае составляются по следующему мнемоническому правилу. Производная вероятности любого из состояний системы равна сумме всех потоков вероятности, переводящих систему в это состояние, за вычетом суммы всех потоков вероятности, выводящих систему из этого состояния.
В пределе при 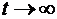 в системе, описываемой линейными дифференциальными уравнениями (1.2.3), в некоторых случаях может установиться режим, в ходе которого система случайным образом меняет свои состояния (или, как говорят, бесконечно блуждает по всем своим состояниям), но их вероятностные характеристики уже не зависят от времени. Говоря другими словами, в этом случае существуют так называемые предельные (или финальные) вероятности стационарных состояний системы pj , и при этом
в системе, описываемой линейными дифференциальными уравнениями (1.2.3), в некоторых случаях может установиться режим, в ходе которого система случайным образом меняет свои состояния (или, как говорят, бесконечно блуждает по всем своим состояниям), но их вероятностные характеристики уже не зависят от времени. Говоря другими словами, в этом случае существуют так называемые предельные (или финальные) вероятности стационарных состояний системы pj , и при этом
|
|
lim 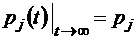 , j = 0, 1, 2, … n.
, j = 0, 1, 2, … n.
Заметим, что предельную вероятность состояния j в этом случае можно трактовать и как среднее относительное время пребывания системы в этом состоянии.
Для вычисления предельных вероятностей нужно, очевидно, все левые части в уравнениях Колмогорова (1.2.3) положить равными нулю и решить полученную систему линейных, но уже алгебраических, а не дифференциальных уравнений
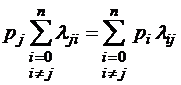 , j = 0, 1, 2, … n (1.2.4)
, j = 0, 1, 2, … n (1.2.4)
(уравнения равновесия соответствующего марковского процесса). При этом стационарный режим существует тогда и только тогда, когда данная система уравнений имеет хотя бы одно ненулевое и вместе с тем не обращающееся в бесконечность решение  , j = 0, 1, 2, … n. Легко видеть, что система (1.2.4) представляет собой систему линейных однородных, то есть не имеющих свободного члена, алгебраических уравнений для вероятностей стационарных состояний p 0, p 1, … pn. Но, как известно из линейной алгебры, такая система уравнений имеет бесчисленное множество решений и позволяет определить неизвестные величины pj только с точностью до некоторого произвольного множителя. В рассматриваемом случае решение, оче-
, j = 0, 1, 2, … n. Легко видеть, что система (1.2.4) представляет собой систему линейных однородных, то есть не имеющих свободного члена, алгебраических уравнений для вероятностей стационарных состояний p 0, p 1, … pn. Но, как известно из линейной алгебры, такая система уравнений имеет бесчисленное множество решений и позволяет определить неизвестные величины pj только с точностью до некоторого произвольного множителя. В рассматриваемом случае решение, оче-
видно, становится единственным, если добавить к системе (1.2.4) условие нормировки
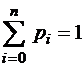 ,
,
взамен которого можно из системы (1.2.4) устранить любое другое, поскольку одно из уравнений этой системы зависит от остальных.
В курсах линейной алгебры доказывается, что такая система имеет одно единственное решение, то есть однозначно определяет вероятности p 0, p 1, …, дающие в сумме единицу. Заметим, что с точки зрения математики вышеописанные действия эквивалентны следующей, подчас более простой, процедуре. А именно, если существует хотя бы одно такое решение 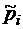 системы уравнений (1.2.4), для которого выполнено неравенство
системы уравнений (1.2.4), для которого выполнено неравенство
|
|
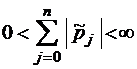 ,
,
то стационарное распределение вероятностей определяется однозначно по формуле
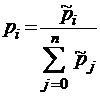 , i = 0, 1, 2, … n.
, i = 0, 1, 2, … n.
|
|
|

Папиллярные узоры пальцев рук - маркер спортивных способностей: дерматоглифические признаки формируются на 3-5 месяце беременности, не изменяются в течение жизни...

Археология об основании Рима: Новые раскопки проясняют и такой острый дискуссионный вопрос, как дата самого возникновения Рима...

Общие условия выбора системы дренажа: Система дренажа выбирается в зависимости от характера защищаемого...

Двойное оплодотворение у цветковых растений: Оплодотворение - это процесс слияния мужской и женской половых клеток с образованием зиготы...
© cyberpedia.su 2017-2024 - Не является автором материалов. Исключительное право сохранено за автором текста.
Если вы не хотите, чтобы данный материал был у нас на сайте, перейдите по ссылке: Нарушение авторских прав. Мы поможем в написании вашей работы!