1. 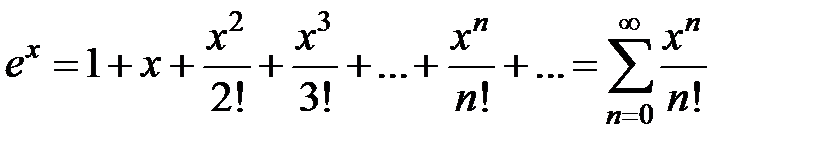 , x Î R.
, x Î R.
2. 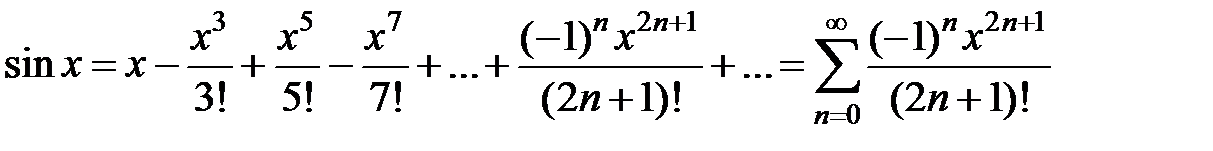 , x Î R
, x Î R
3.  , x Î R
, x Î R
4. 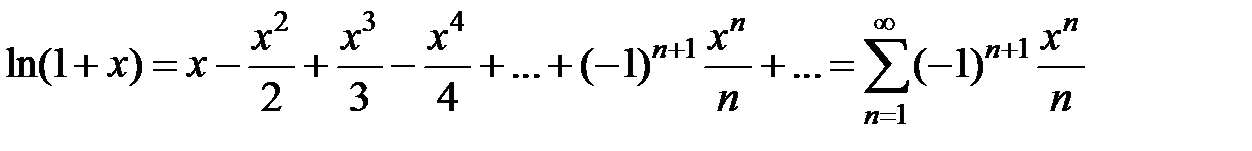 , x Î (−1;1].
, x Î (−1;1].
5. 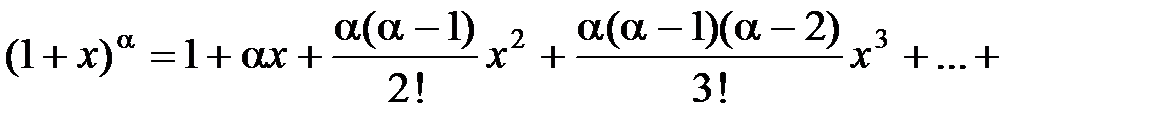
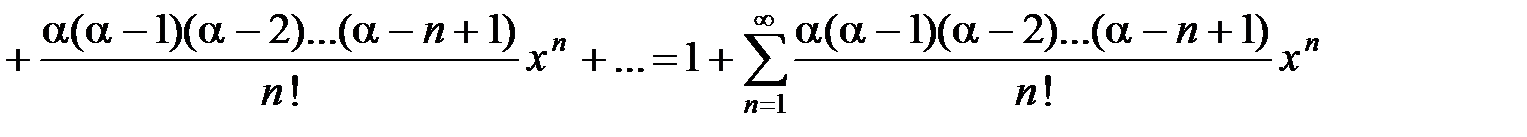 , x Î (−1;1).
, x Î (−1;1).
Пример 9. Разложить функцию f (x) = x 3+ 2 x – 5 по степеням x – 1.
3Воспользуемся формулой (21), в которой надо взять x 0= 1, n = 3 (n – степень многочлена). Вычислим f (1), f /(1), f //(1), f ///(1) и полученные числа подставим в формулу (21).
f (1) = –2,
f /(x) = 3 x 2+2, f /(1) = 5,
f //(x) = 6 x, f //(1) = 6,
f ///(x) = 6.
После подстановки в (21), в которой вместо x – x 0надо писать x – 1, окончательно получим x 3+ 2 x – 5 = –2 + 5(x – 1) +3(x – 1)2+ (x – 1)3.4
Пример 10. Разложить функцию  в ряд по степеням x.
в ряд по степеням x.
3По формуле суммы геометрической прогрессии
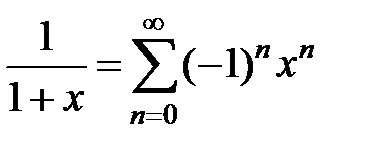 . (36)
. (36)
Ряд сходится при | x | < 1.4
Пример 11. Разложить в ряд по степеням (x + 3) функцию ln(2 – 5 x).
3Рассмотрим сначала следующее преобразование данной логарифмической функции:
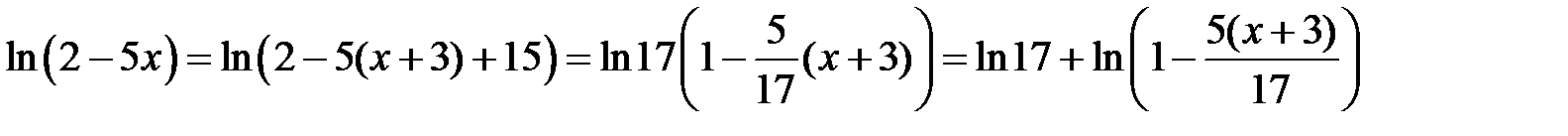 .
.
Воспользуемся разложением (34) для функции ln(1 + t) и положим 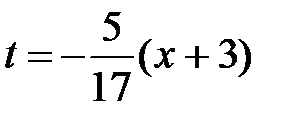 . Так как разложение (34) имеет место при x Î (–1;1], то наше разложение будет иметь место при
. Так как разложение (34) имеет место при x Î (–1;1], то наше разложение будет иметь место при 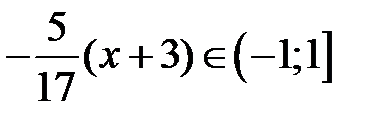 . Таким образом,
. Таким образом, 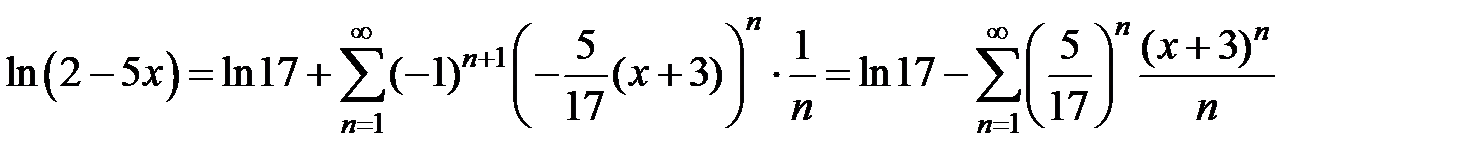 ,
,
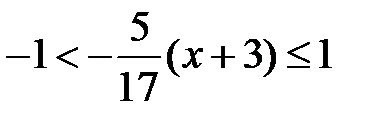 , т.е. ряд сходится при
, т.е. ряд сходится при 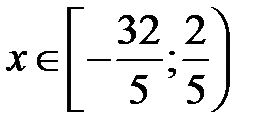 .4
.4
При разложении в ряд Тейлора часто используют почленное дифференцирование и интегрирование степенных рядов.
Пример 12. Разложить в ряд Маклорена функцию f (x) = arctg x.
3Найдем производную f (x), получим
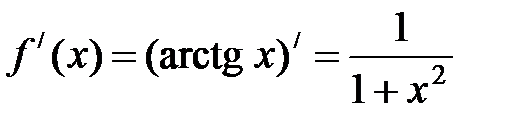 .
.
Заменив в формуле (36) x на x 2, получим
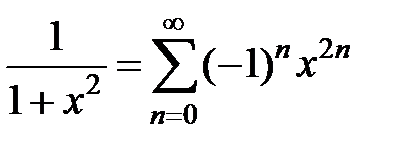 для x Î (–1;1).
для x Î (–1;1).
Интегрируя этот ряд почленно, получаем
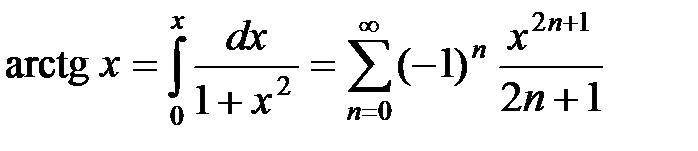 .
.
Так как при почленном интегрировании интервал сходимости сохраняется, то 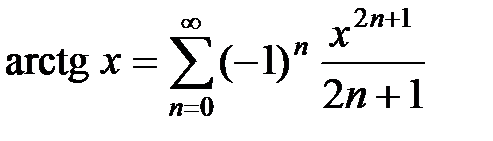 для любого x Î (–1;1].4
для любого x Î (–1;1].4
Используя разложения основных элементарных функций, а также возможность почленного дифференцирования и интегрирования степенных рядов, разложить функции в ряд по степеням 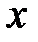 и указать области сходимости полученных рядов.
и указать области сходимости полученных рядов.
227. 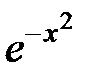 . .
| 228. 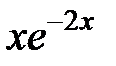 . .
|
229.  . .
| 230. 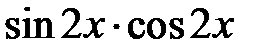 . .
|
231. 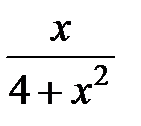 . .
| 232. 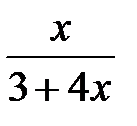 . .
|
233. 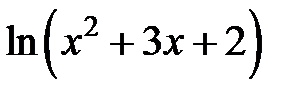 . .
| 234. 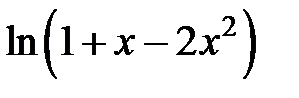 . .
|
235. 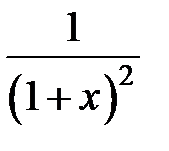 . .
| 236. 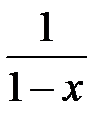 . .
|
237. 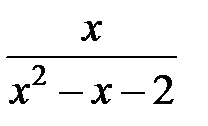 . .
| 238. 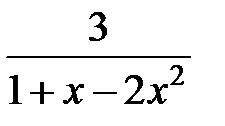 . .
|
239. 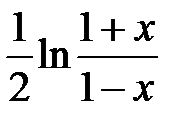 . .
| 240. 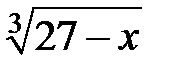 . .
|
241. 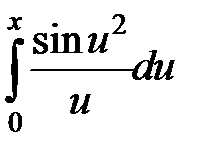 . .
| 242.  . .
|
Разложить функции в ряд по степеням 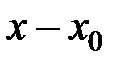 и определить области сходимости полученных рядов.
и определить области сходимости полученных рядов.
243. 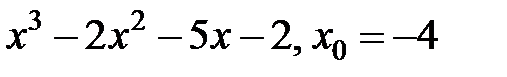 . .
| 244. 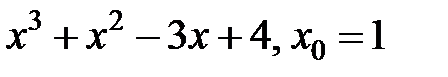 . .
|
245. Разложить в ряд Маклорена функцию 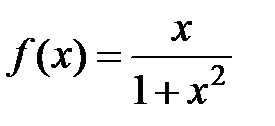 и из полученного ряда почленным дифференцированием получить ряд Маклорена для функции
и из полученного ряда почленным дифференцированием получить ряд Маклорена для функции 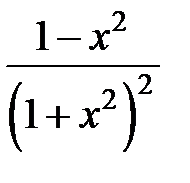 .
.
9.246. Разложить в ряд Маклорена функцию 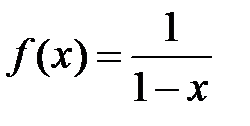 и из полученного ряда почленным дифференцированием получить ряд Маклорена для функции
и из полученного ряда почленным дифференцированием получить ряд Маклорена для функции  .
.
Задачи повышенной сложности
Разложить функции в ряд по степеням 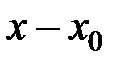 и определить области сходимости полученных рядов.
и определить области сходимости полученных рядов.
247. 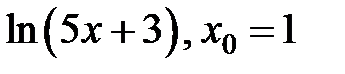 . .
| 248. 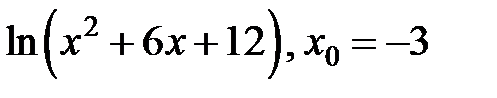 . .
|
249.  . .
| 250. 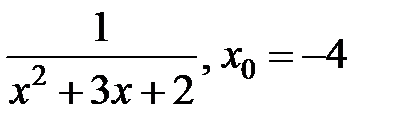 . .
|
251. 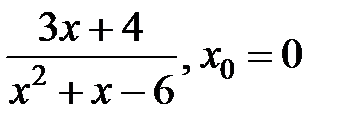 . .
| 252. 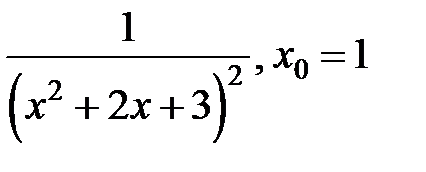 . .
|
253. 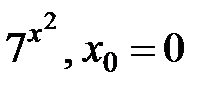 . .
| 254. 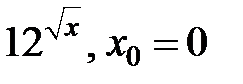 . .
|
9.255. 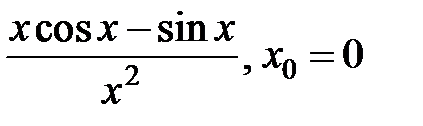 . .
| 256. 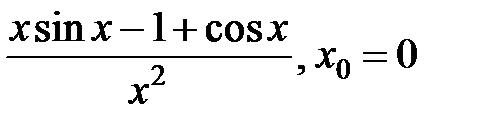 . .
|
Используя возможность почленного интегрирования степенных рядов, разложить в ряд Маклорена следующие функции:
257. 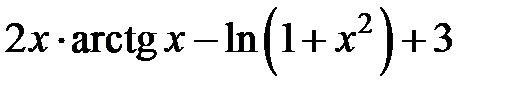 .
.
258. 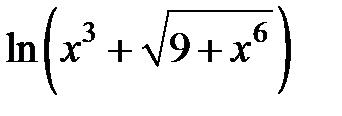 .
.
6.3. Применение степенных рядов
1) Приближенное вычисление значений функции.
Если функция f (x) в интервале (x 0– R; x 0+ R) разлагается в степенной ряд  , то в качестве приближенного значения функции f (x) в точке x Î (x 0– R; x 0+ R) можно взять частичную сумму этого ряда:
, то в качестве приближенного значения функции f (x) в точке x Î (x 0– R; x 0+ R) можно взять частичную сумму этого ряда: 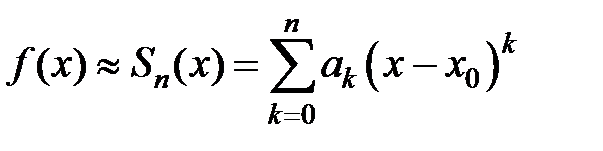 . Точность этого равенства увеличивается с ростом n. Абсолютная погрешность этого приближенного равенства равна модулю остатка ряда, т.е.
. Точность этого равенства увеличивается с ростом n. Абсолютная погрешность этого приближенного равенства равна модулю остатка ряда, т.е.
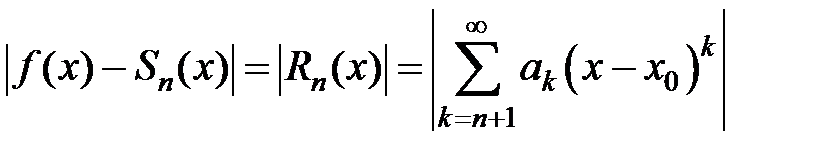 .
.
Оценивать остаток ряда можно различными способами. Можно использовать представление остаточного члена формулы Тейлора в форме Лагранжа, Коши или интегральной (см. гл. 4 §3). Можно, кроме того, строить для ряда числовую мажоранту, сумму которой несложно вычислить. В отдельных случаях можно применять признак Лейбница: если степенной ряд в некоторой точке x удовлетворяет признаку Лейбница, то
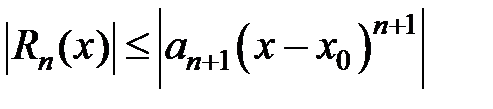 .
.
Пример 13. Вычислить число e с точностью до 0,001.
3Подставив x = 1 в формулу (12), имеем 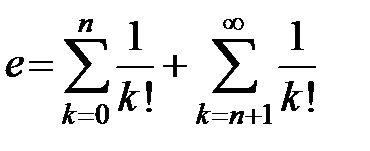 .
.
Оценим остаток
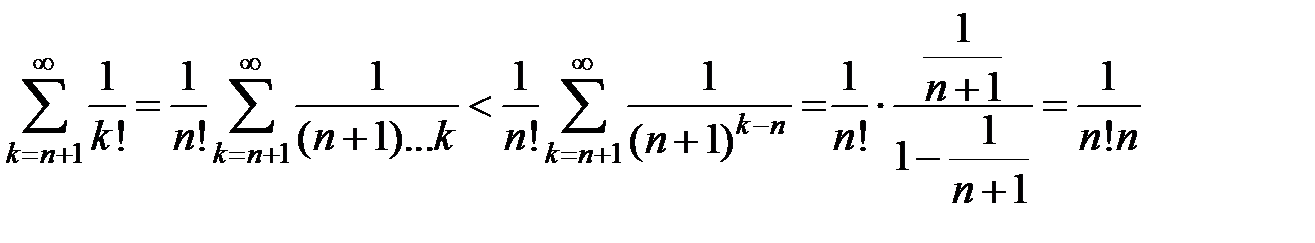 .
.
Следовательно, равенство 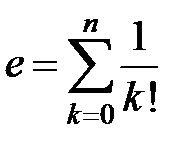 имеет абсолютную погрешность, равную
имеет абсолютную погрешность, равную 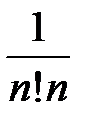 . Найдем n, для которого
. Найдем n, для которого 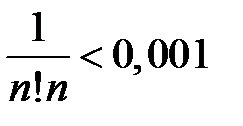 или n! n > 1000. Получаем n ³ 6. Вычисляя
или n! n > 1000. Получаем n ³ 6. Вычисляя 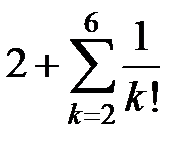 и округляя, находим ответ с требуемой точностью e» 2,718.4
и округляя, находим ответ с требуемой точностью e» 2,718.4
259. Определить, сколько нужно взять членов в разложении функции 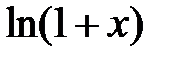 , чтобы вычислить
, чтобы вычислить  с точностью до
с точностью до 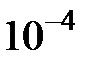 .
.
260. Определить, сколько нужно взять членов ряда в разложении функции 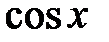 , чтобы вычислить
, чтобы вычислить 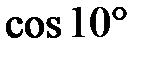 с точностью до
с точностью до 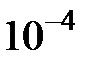 .
.
Используя соответствующие разложения, вычислить указанные значения функций с точностью до 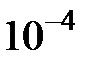 :
:
261. 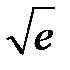 . .
| 262.  . .
|
263. 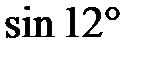 . .
| 264. 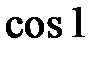 . .
|
Задачи повышенной сложности
Используя соответствующие разложения, вычислить указанные значения функций с точностью до 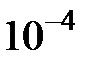 :
:
265. 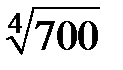 . .
| 266. 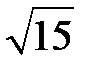 . .
|
267.  . .
| 268. 
|
2) Приближенное вычисление определенных интегралов.
Разлагая подынтегральную функцию f (t) в степенной ряд, можно, используя теорему об интегрировании степенных рядов, представить интеграл 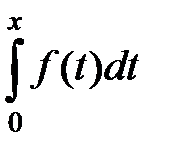 в виде степенного ряда и подсчитать величину этого интеграла с заданной точностью при любом значении
в виде степенного ряда и подсчитать величину этого интеграла с заданной точностью при любом значении 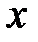 из интервала сходимости полученного ряда.
из интервала сходимости полученного ряда.
Пример 14. Разложить функцию 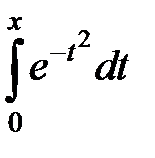 в степенной ряд по степеням x.
в степенной ряд по степеням x.
3Используя разложение 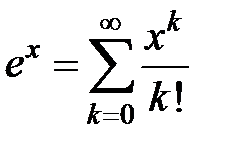 , получим
, получим 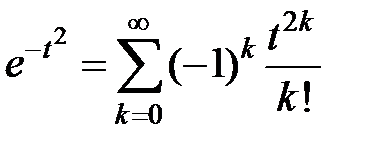 на всей числовой оси. Применяя почленное интегрирование, находим
на всей числовой оси. Применяя почленное интегрирование, находим
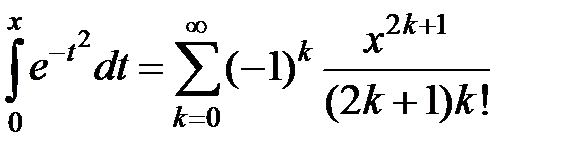 .4
.4
Пример 15. Вычислить  с точностью до 0,001.
с точностью до 0,001.
3Известно, что первообразная для функции 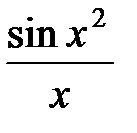 не выражается через элементарные функции. Разложим подынтегральную функцию в степенной ряд, используя разложение (31):
не выражается через элементарные функции. Разложим подынтегральную функцию в степенной ряд, используя разложение (31):
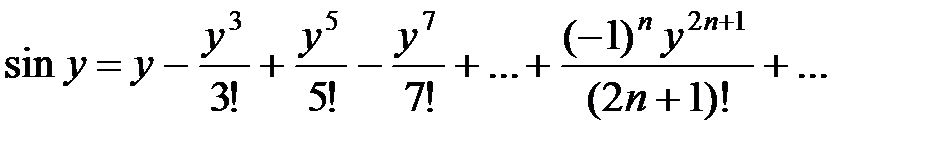
Подставляя вместо y x 2, получаем
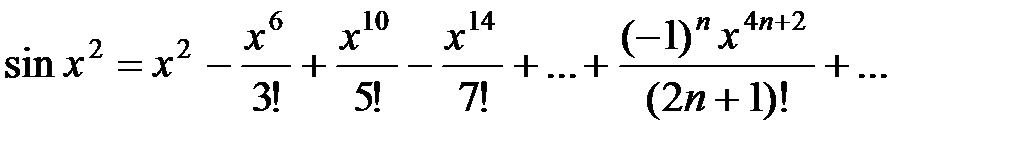
Тогда
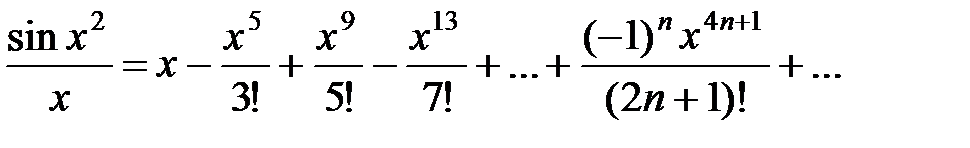
Интегрируя обе части этого равенства, получим:
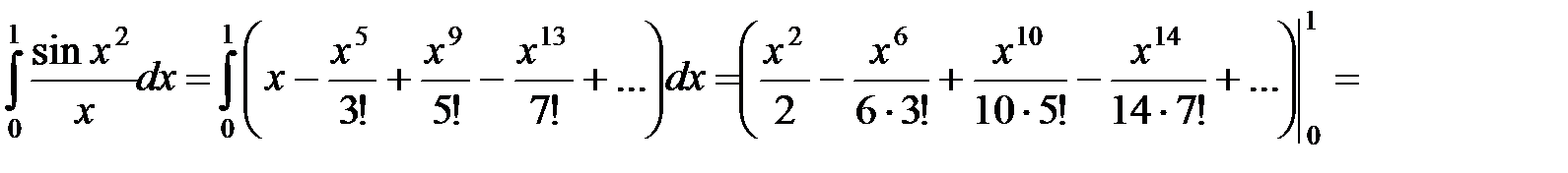
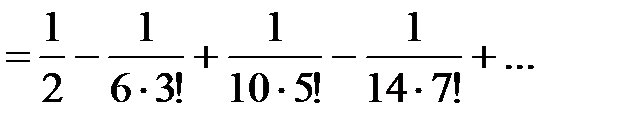
Получили знакочередующийся ряд, удовлетворяющий условиям признака Лейбница. Так как 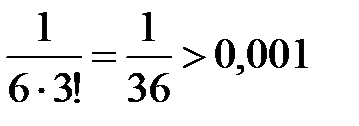 , а
, а 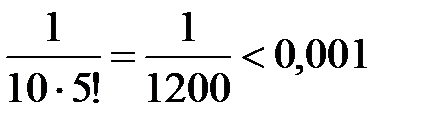 , то с точностью до 0,001 имеем
, то с точностью до 0,001 имеем
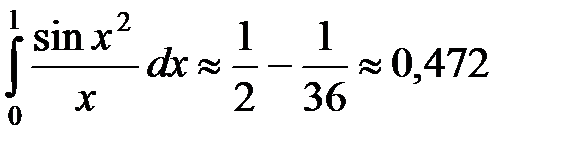 .
.
Разложить указанные функции в степенные ряды по степеням 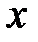 :
:
269. 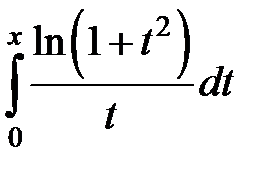 . .
| 270. 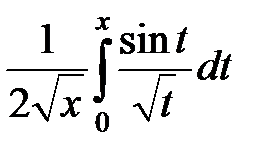 . .
|
9.271. 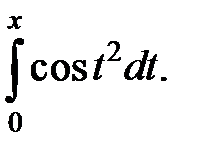
| 9.272. 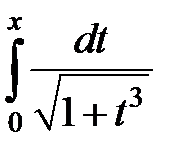
|
Вычислить интегралы с точностью до 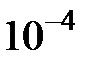 :
:
273. 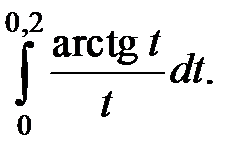
| 274. 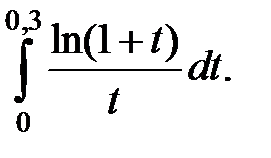
|
275. 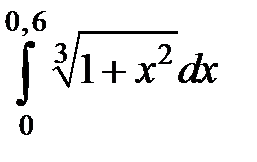 . .
| 276.  . .
|
277. 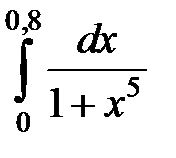 . .
| 278. 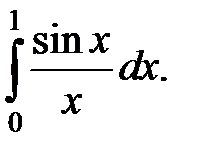
|
3) Интегрирование дифференциальных уравнений с помощью рядов.
Степенные ряды широко применяются при решении дифференциальных уравнений. Для целого ряда дифференциальных уравнений показано, что решение y (x) представимо в виде степенного ряда
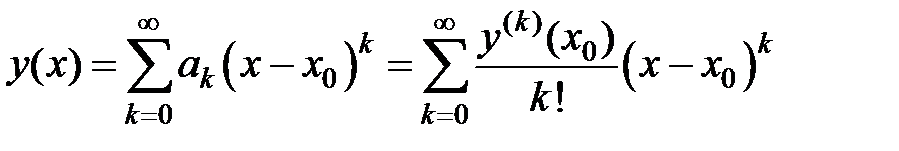 , (18)
, (18)
коэффициенты которого можно определить с учетом заданного уравнения различными способами.
а) Способ последовательного дифференцирования.
Пусть требуется найти решение уравнения y //= f (x, y, y /), удовлетворяющее условиям y (x 0) = y 0, y /(x 0) = y 1, причем функция f (x, y, y /) в точке (x 0, y 0, y 1) имеет частные производные любого порядка. Тогда коэффициенты y ( k )(x 0) ряда (18) определяются путем последовательного дифференцирования исходного уравнения и подстановки в него x 0и найденных уже значений y /(x 0), y //(x 0),…
Пример 16. Найти решение уравнения y //= x 2 y, удовлетворяющее условиям y (0) = 0, y /(0) = 1.
3Имеем y (0) = 0, y /(0) = 1, из заданного уравнения найдем y //(0) = 0. Далее, дифференцируя уравнение, имеем
y ///= x 2 y /+ 2 xy,
y (4)= x 2 y //+ 4 x y /+ 2 y,
y (5)= x 2 y ///+ 6 x y //+ 6 y /,
…
y ( k +2)= x 2 y ( k )+ 2 kxy ( k –1)+ k (k – 1) y ( k –2),
…
и при x = 0 получаем отсюда
y ( k +2)(0) = k (k – 1) y ( k –2)(0), k = 2,3,…
Так как y (0) = y //(0) = y ///(0) = 0 и y /(0) = 1, то
y (4 n )(0) = y (4 n +2)(0) = y (4 n +3)(0) = 0
и
y (4 n +5)(0) = (4 n + 2)(4 n + 3) y (4 n +1)(0) = 2 × 3 × 6 × 7…(4 n + 2)(4 n + 3), n Î N.
Следовательно,
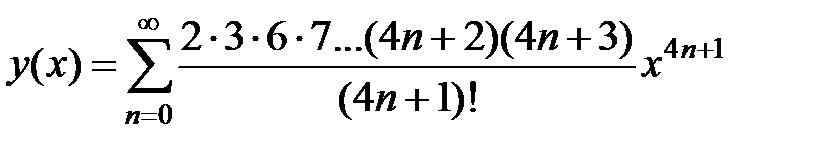 .
.
По признаку Даламбера полученный ряд сходится для любых x Î R, а определяемая этим рядом функция y (x) является решением заданного уравнения при любых x. 4
б) Способ неопределенных коэффициентов.
Если исходное дифференциальное уравнение линейно относительно искомой функции и ее производных, причем коэффициент при старшей производной в точке x 0отличен от нуля, то решение следует искать в виде ряда (18) с неопределенным коэффициентами ak, k = 0,1,…
Пример 17. Найти решение (в виде степенного ряда) уравнения
y //– xy /+ y = 1, удовлетворяющее условиям y (0) = y /(0) = 0.
3Ищем решение в виде ряда 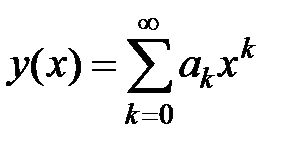 , в котором в силу условий y (0) = y /(0) = 0 имеем a 0= a 1= 0. Следовательно,
, в котором в силу условий y (0) = y /(0) = 0 имеем a 0= a 1= 0. Следовательно, 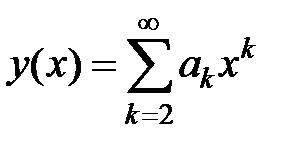 . Подставив это выражение в уравнение, получаем
. Подставив это выражение в уравнение, получаем
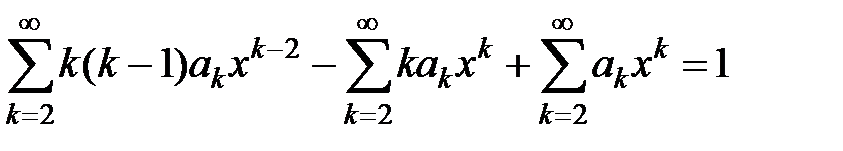 .
.
Отсюда находим, что 2 × 1 × a 2= 1, т.е. 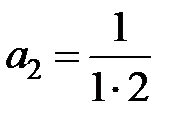 , и (k + 1)(k + 2) ak +2= =(k – 1) ak для k = 1, 2,… Так как a 1= 0, то a 2 m +1= 0 для всех m = 0, 1,…, а для k = 2 m, m = 1, 2,…, получаем рекуррентную формулу
, и (k + 1)(k + 2) ak +2= =(k – 1) ak для k = 1, 2,… Так как a 1= 0, то a 2 m +1= 0 для всех m = 0, 1,…, а для k = 2 m, m = 1, 2,…, получаем рекуррентную формулу
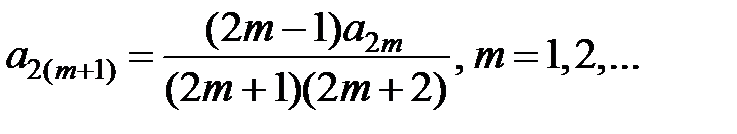 ,
,
из которой выводим равенства
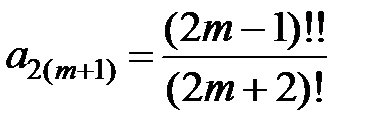 .
.
Следовательно, искомое решение имеет вид
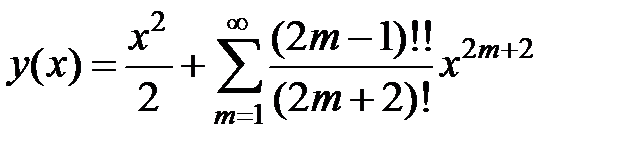 ,
,
причем полученный ряд сходится при всех x Î R.4
Найти решения уравнений, удовлетворяющие заданным условиям:
279.  .
.
9.280. 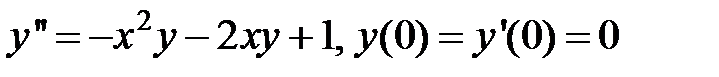 .
.
Найти первые пять членов разложения решения дифференциального уравнения в степенной ряд:
281. 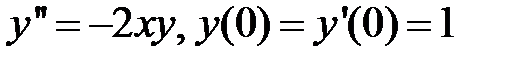 .
.
282. 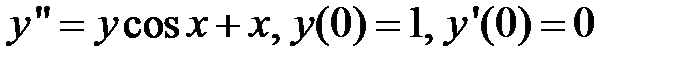 .
.
Найти решение уравнений, удовлетворяющие заданным условиям:
283. 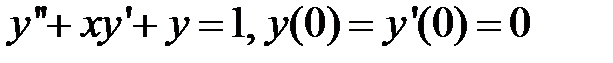 .
.
284. 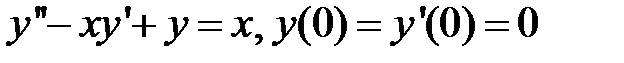 .
.
285. 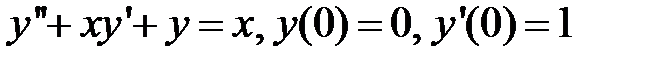 .
.
286. 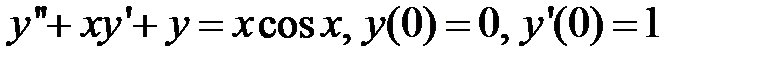 .
.
РЯДЫ ФУРЬЕ
Ряды Фурье
7.1. Тригонометрические ряды. Ортогональность тригонометрической системы
Определение. Тригонометрическим рядом называется функциональный ряд вида
 (1)
(1)
где числа a 0,… an, bn (n = 1,2,…) называются коэффициентами ряда.
Теорема. Тригонометрическая система функций
1, cos x, sin x, cos2 x, sin2 x,…, cos nx, sin nx (2)
является ортогональной на отрезке [–p; p], т.е. интеграл по этому отрезку от произведения любых двух различных функций этой системы равен нулю, а интеграл по отрезку [–p; p] от квадрата любой функции этой системы отличен от нуля.
Доказательство. Действительно, для любых целых k, n ¹ 0 (k ¹ n) имеем:
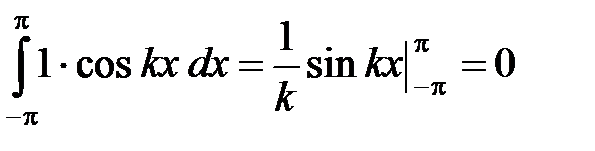 ,
, 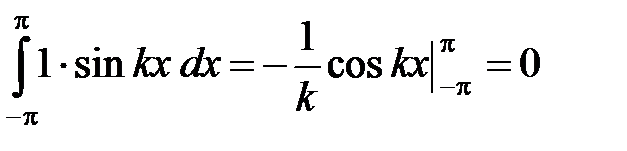 , (3)
, (3)
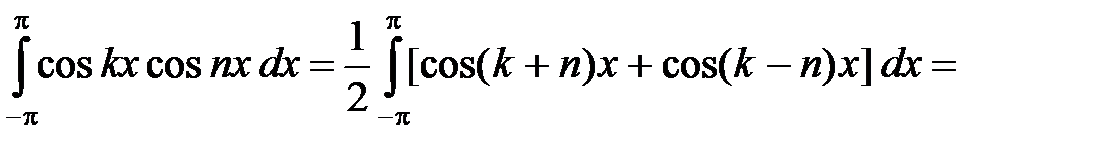
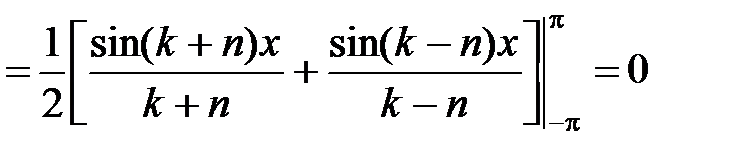 . (4)
. (4)
Аналогично
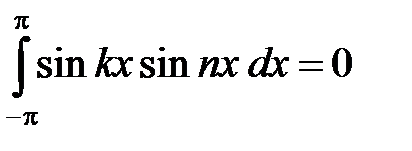 и
и 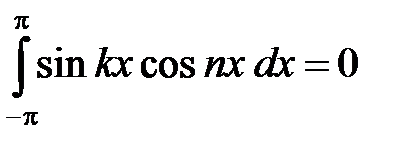 . (5)
. (5)
Наконец,  ,
,
 , (6)
, (6)
 . ■
. ■
7.2. Коэффициенты Фурье. Ряд Фурье
Теорема. Если функция f (x), интегрируемая на отрезке [–p; p], разлагается в тригонометрический ряд
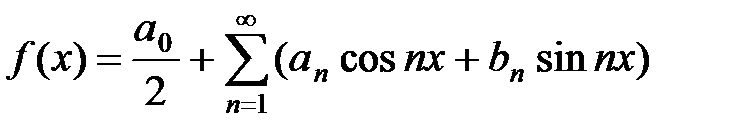 , (7)
, (7)
который можно интегрировать почленно, то это разложение единственно.
Доказательство. Интегрируя (7), получим:
 ,
,
откуда, учитывая (3), находим:
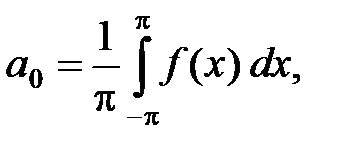 (8)
(8)
Для определения коэффициента an при cos nx умножим равенство (7) (в котором предварительно переобозначим индекс суммирования n на k) на cos nx. Получим
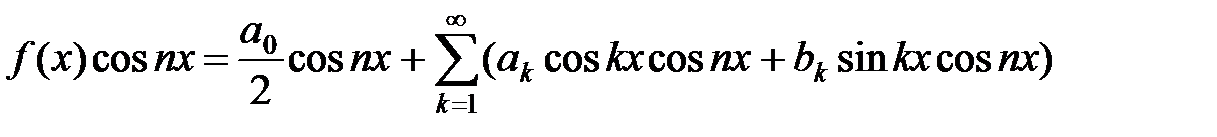 . (9)
. (9)
Т.к. каждый член этого ряда по абсолютной величине не превышает соответствующих членов ряда (7), то этот ряд тоже можно почленно интегрировать. Проинтегрируем соотношение (9) по х от –p до p. Учитывая формулы (3) – (6), получим:
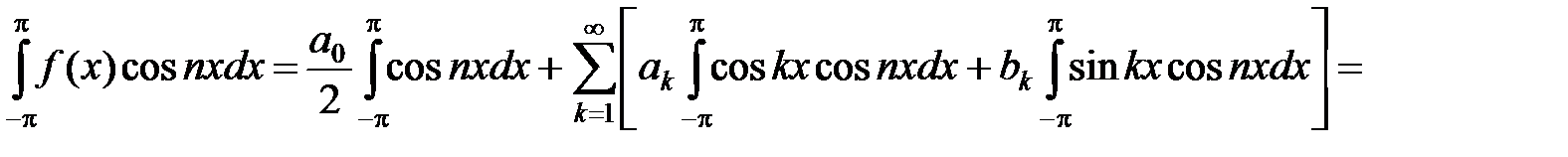
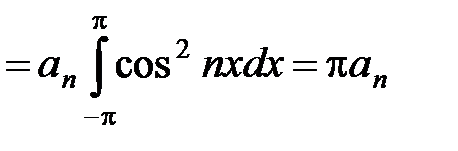 , откуда
, откуда
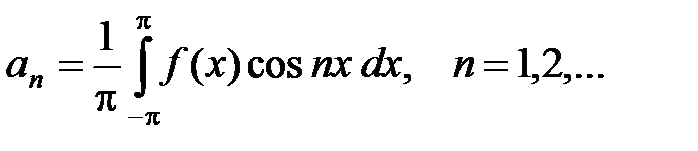 (10)
(10)
Аналогично, умножая равенство (7) на sin nx и интегрируя в пределах от –p до p, на основании тех же формул получаем
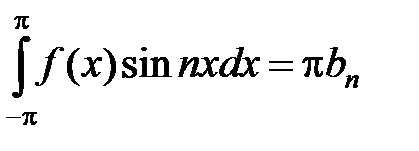 , откуда находим
, откуда находим
 (11)
(11)
Таким образом, коэффициенты a 0, an, bn ряда (7) определяются по формулам (8), (10), (11) единственным образом. Теорема доказана. ■
Определение. Пусть f (x) интегрируемая на отрезке [–p; p] функция. Тогда числа a 0, an, bn, найденные по формулам (8), (10), (11), называются коэффициентами Фурье функции f (x). Тригонометрический ряд (1), коэффициенты которого определяются по формулам (8), (10), (11), называется рядом Фурье функции f (x).
Для интегрируемой на отрезке [–p; p] функции f (x) записывают
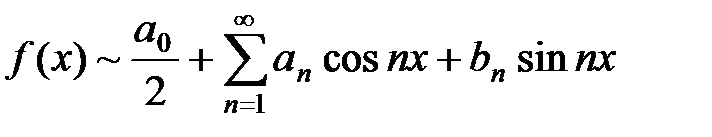
и говорят: функции f (x) соответствует (поставлен в соответствие) её ряд Фурье. Если ряд Фурье сходится, то знак соответствия заменяется знаком равенства.
7.3. Достаточное условие разложимости функции в ряд Фурье (признак Дирихле)
Определение. Функция f (x) называется кусочно-монотонной наотрезке [ a, b ], если этот отрезок можно разбить конечным числом точек x 1, x 2,…, xn –1на интервалы (a, x 1), (x 1, x 2),…, (xn –1, b) так, что на каждом из интервалов функция монотонна.
Заметим, что если функция f (x) кусочно-монотонная и ограниченная на отрезке [ a, b ], то она может иметь точки разрыва только первого рода.
Теорема (Признак Дирихле). Если 2p периодическая функция f (x) является кусочно-монотонной и ограниченной на отрезке [–p; p], то её ряд Фурье сходится во всех точках. Сумма этого ряда равна значению функции f (x) в точках непрерывности функции и значению  в точках разрыва.
в точках разрыва.
7.4. Разложение в ряд Фурье четных и нечетных функций
1) Пусть функция f (x) определена на отрезке [–p; p]. Если функция четная, т.е. f (– x) = f (x), то её ряд Фурье имеет вид
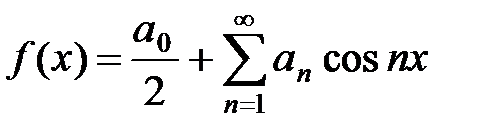 , (12)
, (12)
где  ,
, 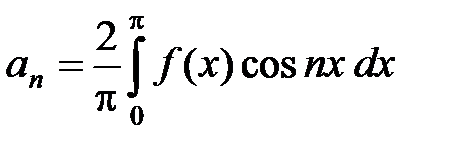 , n Î N,
, n Î N,
а коэффициенты Фурье bn = 0.
Действительно,
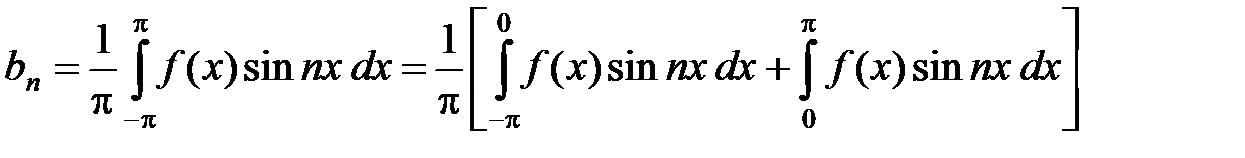 .
.
В первом интеграле в квадратных скобках сделаем замену переменной x = – t. Тогда dx = – dt, а пределы интегрирования станут от p до 0. Принимая во внимание, что функция f (x) – четная, а функция sin x – нечетная, получаем
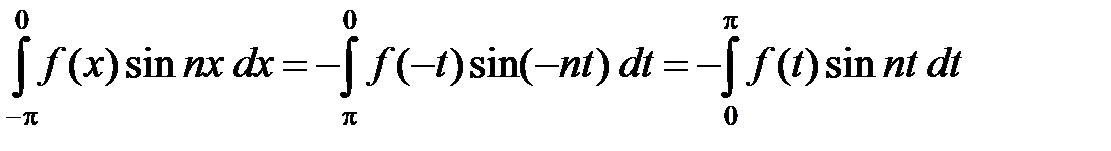 .
.
Следовательно,  .
.
Аналогично, учитывая, что функции f (x) и cos х четные, можно получить записанные выше выражения для коэффициентов аn.
2) Пусть теперь функция f (x), определенная на отрезке [–p; p], нечетная, т.е. f (– x) = – f (x) то её ряд Фурье имеет вид
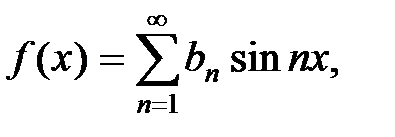
где 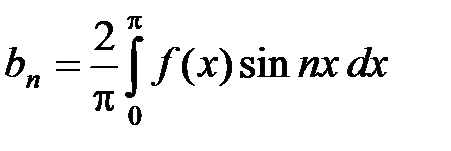 , n Î N, (13)
, n Î N, (13)
а коэффициенты Фурье аn = 0.
Рассуждения здесь такие же, как и в случае 1).
Таким образом, если функция f (x) четная, то ряд Фурье содержит только косинусы, а если нечетная, то только синусы.
Пример 1. Разложить ряд Фурье функцию
f (
x) = sign
x, –p <
x < p и, пользуясь разложением, найти сумму ряда Лейбница
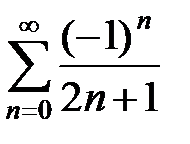
.
3Продолжая периодически функцию f (x) на всю вещественную ось, получим функцию  , график которой изображен на рисунке. Эта функция 2p-периодическая, кусочно-монотонная и ограниченная, значит, согласно признаку Дирихле она разложима в ряд Фурье. Вычислим коэффициенты Фурье функции f (x). Так как функция нечетная, то an = 0, n = 0,1,…, а коэффициенты bn находится по формуле (13):
, график которой изображен на рисунке. Эта функция 2p-периодическая, кусочно-монотонная и ограниченная, значит, согласно признаку Дирихле она разложима в ряд Фурье. Вычислим коэффициенты Фурье функции f (x). Так как функция нечетная, то an = 0, n = 0,1,…, а коэффициенты bn находится по формуле (13):
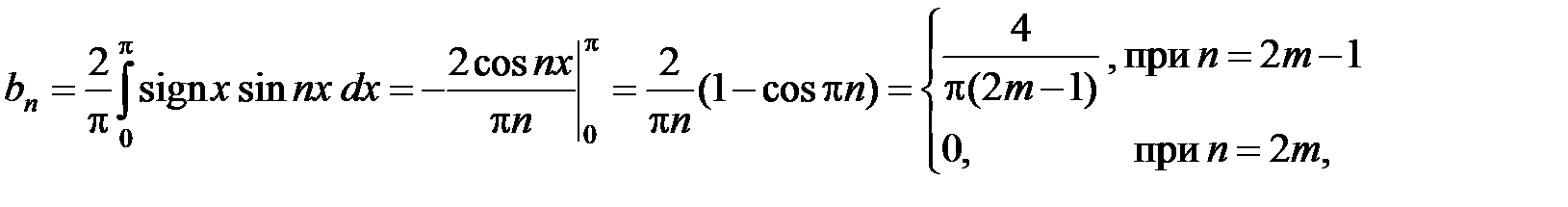
где m Î N. Следовательно, при –p < x < p
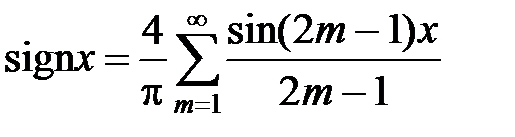 ,
,
откуда при 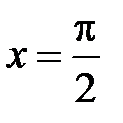 получаем
получаем 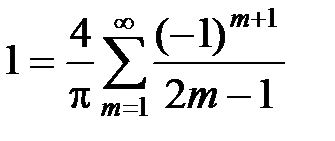 , т.е.
, т.е. 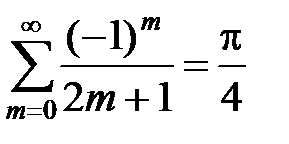 .
.
Отметим, что вне интервала (–p; p) полученный ряд сходится к функции  : в точках непрерывности функции
: в точках непрерывности функции  ряд Фурье будет сходиться к значению функции в этой точке, а в точках разрыва x = p n, где n Î Z, функция
ряд Фурье будет сходиться к значению функции в этой точке, а в точках разрыва x = p n, где n Î Z, функция  не определена, а сумма ряда Фурье равна нулю.4
не определена, а сумма ряда Фурье равна нулю.4
Пример 2. Разложить в ряд Фурье функцию f (x) = x 2на отрезке [–p; p].
3Продолжая периодически функцию
f (
x) на всю вещественную ось, получим функцию

, график которой изображен на рисунке. Эта функция 2p-периодическая, непрерывная и ограниченная, следовательно, может быть разложена в ряд Фурье. Так как она четная, то её коэффициенты Фурье
bn = 0, а
an находится по формулам (11):
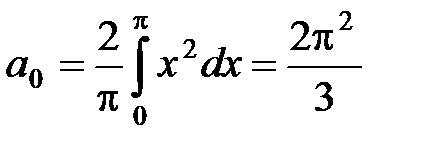 ,
,
 .
.
Значит, ряд Фурье данной функции имеет вид
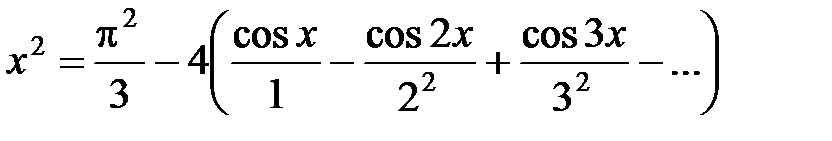 .
.
Это разложение справедливо для любого x Î [–p; p], так как в данном случае в точках x = ±p сумма ряда совпадает со значениями функции f (x) = x 2, поскольку  .
.
В силу непрерывности функции  для всех значений х Î R ее ряд Фурье в любой точке будет сходиться к значению функции в этой точке.4
для всех значений х Î R ее ряд Фурье в любой точке будет сходиться к значению функции в этой точке.4
7.5. Разложение в ряд Фурье функций с произвольным периодом
Пусть теперь функция f (x) является периодической с произвольным периодом 2 l, l ¹ 0. Отметим, что признак Дирихле, сформулированный в п. 7.4, для 2p-периодических функций, справедлив и для функций с произвольным периодом.
Пусть функция f (x) интегрируема на отрезке [– l; l ] (где l > 0). Тогда ряд Фурье функции f (x) имеет вид
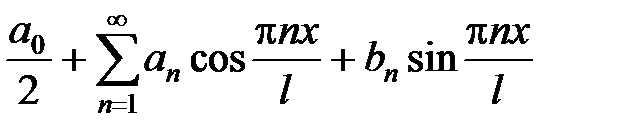 , (14)
, (14)
где 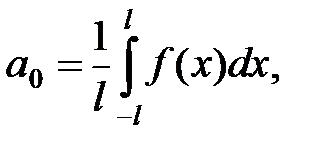
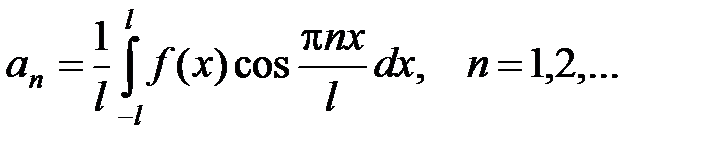 ,
,
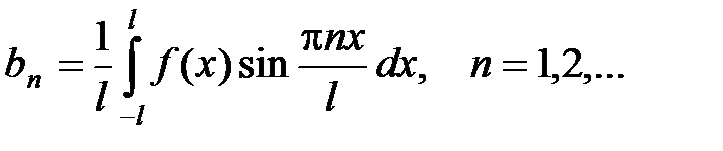
Если функция f (x), кроме того, непрерывна, то
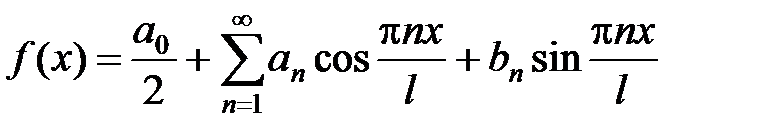 .
.
Для доказательства (14) сделаем замену переменной  . Тогда функция
. Тогда функция 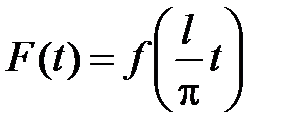 будет периодической функцией аргумента t с периодом 2p, так как
будет периодической функцией аргумента t с периодом 2p, так как
 ,
,
и ее можно разложить на отрезке [–p; p] в ряд Фурье
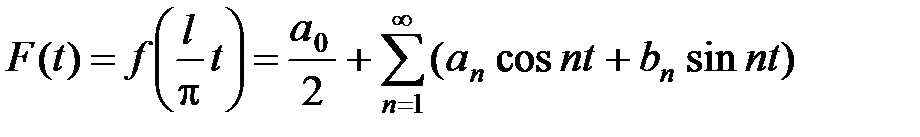 ,
,
где
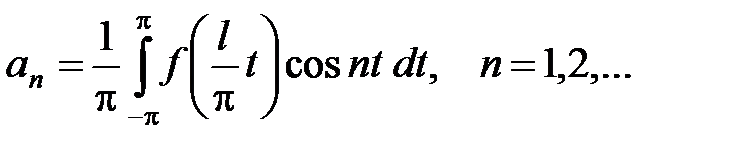

Возвращаясь к переменной х, т.е. положив 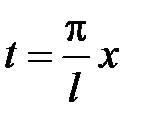 ,
, 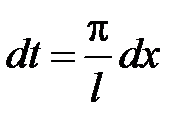 , получим ряд (14) с соответствующими коэффициентами.
, получим ряд (14) с соответствующими коэффициентами.
Пример 3. На отрезке [–3; 3] найти тригонометрический ряд Фурье функции f (x) = | x |.
3 Продолжая периодически функцию
f (
x) на всю вещественную ось, получим функцию

, график которой изображен на рисунке. Эта функция периодическая с периодом 2
l = 6, непрерывная и ограниченная, следовательно, может быть разложена в ряд Фурье. Кроме того, функция
f (
x) = |
x | – четная, следовательно, все коэффициенты Фурье
bn = 0, а коэффициенты
аn вычисляются следующим образом:
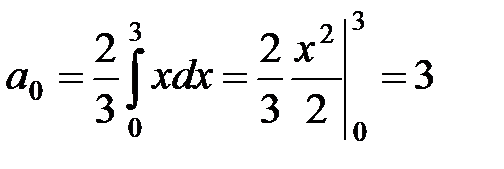 ,
,
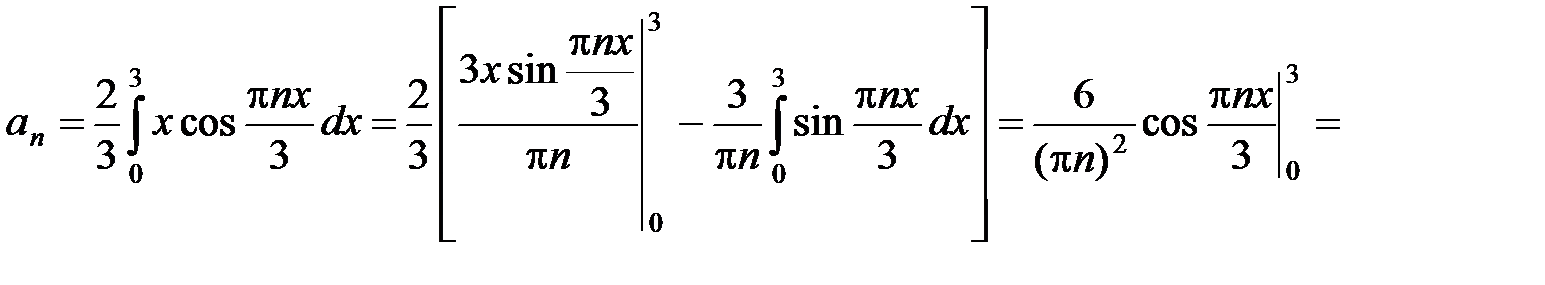
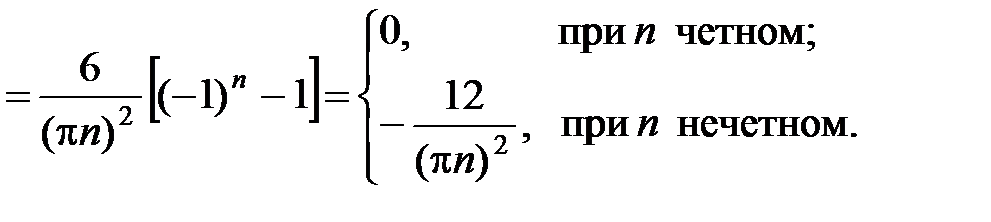
Тогда ряд Фурье функции f (x) на отрезке [–3; 3] имеет вид:
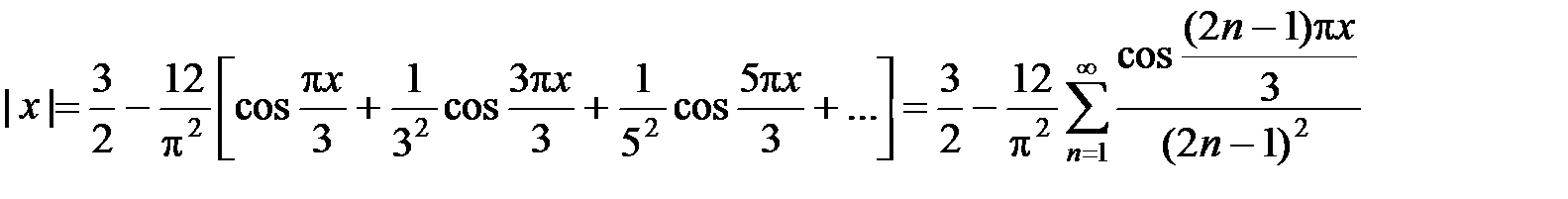 .
.
Так как функция  удовлетворяет условиям признака Дирихле, то ряд Фурье этой функции во всех точках сходится к значению функции.4
удовлетворяет условиям признака Дирихле, то ряд Фурье этой функции во всех точках сходится к значению функции.4
287. Доказать, что ряд Фурье тригонометрического многочлена 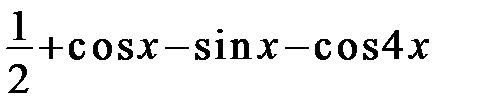 совпадает с этим многочленом.
совпадает с этим многочленом.
288. Доказать, что ряд Фурье тригонометрического многочлена 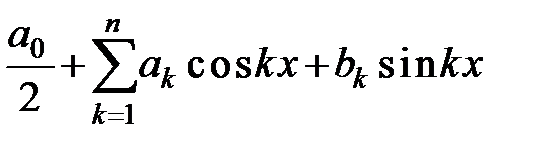 совпадает с этим многочленом.
совпадает с этим многочленом.
289. Найти коэффициент 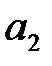 Фурье функции
Фурье функции 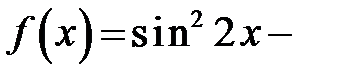
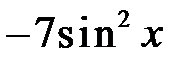 .
.
9.290. Найти коэффициент 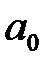 Фурье функции
Фурье функции 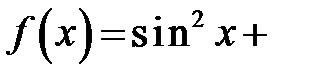
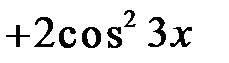 .
.
291. Разложить в ряд Фурье функцию 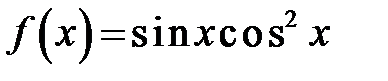 .
.
292. Разложить в ряд Фурье функцию  .
.
293. Вычислить коэффициент 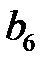 Фурье периодической с периодом
Фурье периодической с периодом 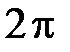 функции
функции 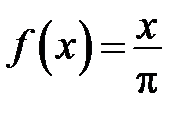 ,
, 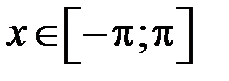 .
.
294. Вычислить коэффициент 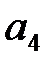 Фурье периодической с периодом
Фурье периодической с периодом 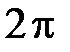 функции
функции  ,
, 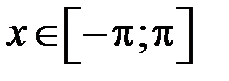 .
.
295. Вычислить коэффициент 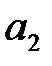 Фурье периодической с периодом 3 функции
Фурье периодической с периодом 3 функции 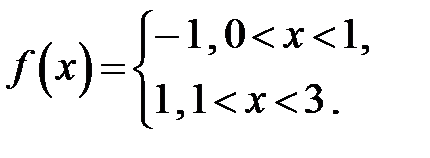
296. Вычислить коэффициент 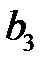 Фурье периодической с периодом 2 функции
Фурье периодической с периодом 2 функции 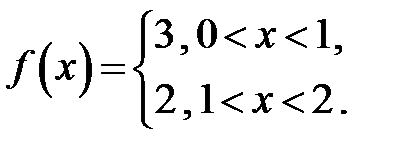
297. Доказать, что если f(x) имеет период 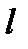 , то
, то 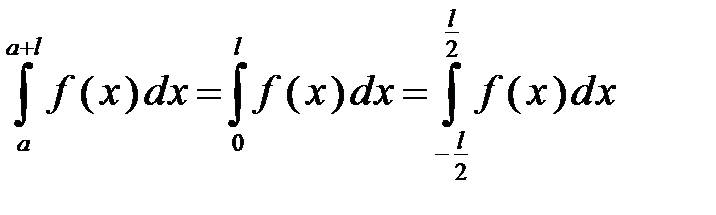 при любом
при любом 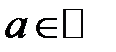 .
.
298. Записать выражение коэффициентов Фурье (28) - (30) для четной и нечетной функций на  .
.
Разложить 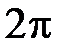 - периодичную функцию в ряд Фурье и найти значение
- периодичную функцию в ряд Фурье и найти значение 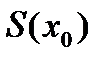 суммы полученного ряда в заданной точке
суммы полученного ряда в заданной точке 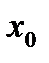 .
.
299. 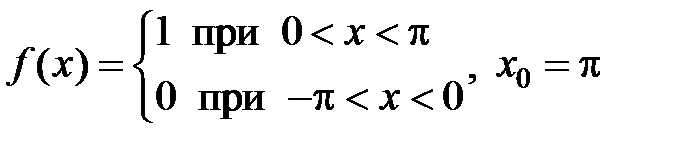 .
.
300. 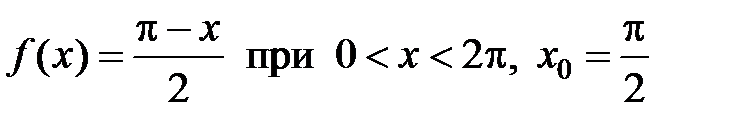 .
.
301. Разложить в ряд Фурье функцию 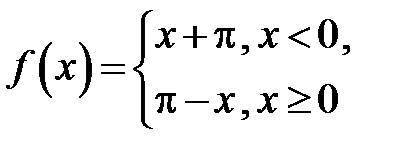 в промежутке
в промежутке 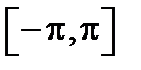 и построить график суммы ряда Фурье этой функции.
и построить график суммы ряда Фурье этой функции.
302. Разложить в ряд Фурье функцию 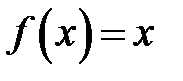 в интервале
в интервале 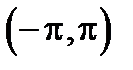 и построить график суммы ряда Фурье этой функции.
и построить график суммы ряда Фурье этой функции.
Разложить в ряд Фурье следующие функции периода 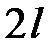 :
:
303. 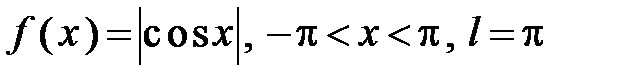 .
.
304. 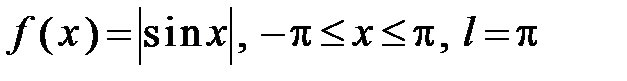 .
.
305. 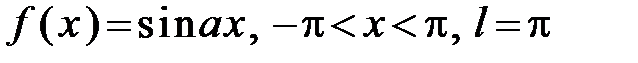 .
.
306. 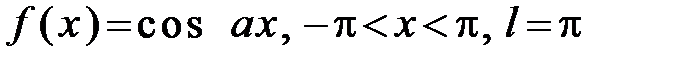 .
.
307. 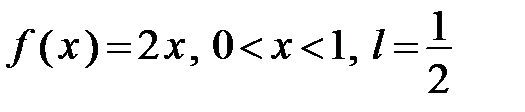 .
.
308. 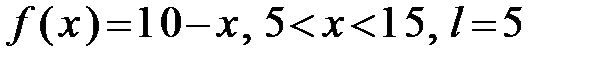 .
.
309. Разложить в ряд Фурье в интервале 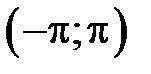 функцию
функцию 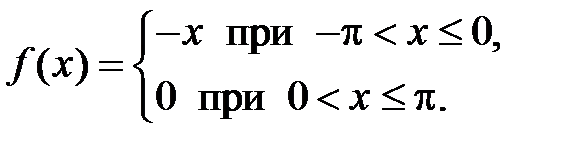
310. Разложить в ряд Фурье в интервале 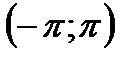 функцию
функцию 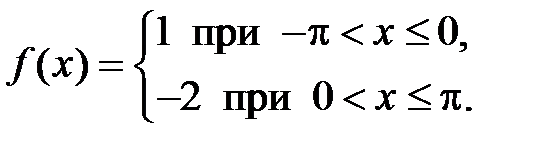
311. Доказать равенство 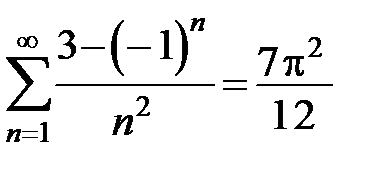 , используя разложение в ряд Фурье функции
, используя разложение в ряд Фурье функции 
312. Доказать равенство 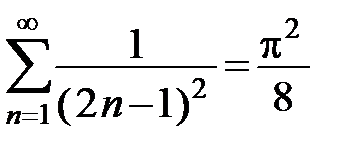 , используя разложение в ряд Фурье функции
, используя разложение в ряд Фурье функции 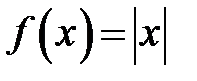 ,
, 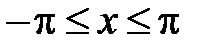 .
.
313. Используя ряд Фурье, полученный в задаче 9.304, найти сумму ряда 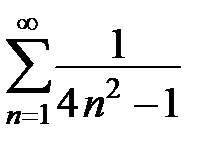 .
.
314. Используя разложение функции 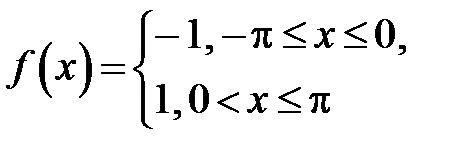 в ряд Фурье, найти сумму ряда
в ряд Фурье, найти сумму ряда 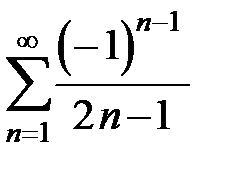 .
.
СПИСОК ЛИТЕРАТУРЫ
1. Пискунов Н.С. Дифференциальное и интегральное исчисления для втузов. Том 1. – М.: Наука, 2010.
2. Кудрявцев Л.Д. Курс математического анализа. Том 1. – М.: Высшая школа, 1981.
3. Тер-Крикоров А.М., Шабунин М.И. Курс математического анализа. М.: Наука, 1988.
4. Никольский С.М. Курс математического анализа. Том 1. – M.: Наука, 1990.
5. Власова Е. А. Ряды. Том IX. – М.: Изд-во МГТУ им. Н.Э. Баумана. 2000.
6. Шипачев В.С. Высшая математика. – М.: Высшая школа, 2010.
7. Фихтенгольц Г. М. Курс дифференциального и интегрального исчисления. Том 2. – М.: Наука, 2010.
8. Беляева, М.А. Ряды. Методические указания к практическим занятиям и к выполнению расчетного задания / М.А.Беляева, А.Г.Мясников, Т.А.Мацеевич. М.: Изд-во МГСУ, 2003.
9. Титова, Т.Н. Числовые и функциональные ряды. Учебное пособие / Т.Н.Титова, Т.А.Мацеевич, Е.Е. Ассеева и др. М.: Изд-во НИУ МГСУ, 2017. 128 с.
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Б
Бином Ньютона, 62
И
Интервал сходимости степенного ряда, 46
К
Коэффициенты
степенного ряда, 43
тригонометрического ряда, 70
Фурье, 72
Критерий Коши сходимости ряда, 9
Круг сходимости степенного ряда, 46
Н
Необходимое условие сходимости, 7
О
Область
абсолютной сходимости функционального ряда, 33
сходимости функционального ряда, 33
Остаток
ряда, 9
функционального ряда, 33
П
Признак
Даламбера, 16
Дирихле, 73
Коши, 18
Коши интегральный, 20
Лейбница, 26
равномерной сходимости функционального ряда Вейерштрасса, 36
сравнения, 11
сравнения предельный, 14
Р
Радиус сходимости степенного ряда, 46
Ряд
абсолютно сходящийся, 25
биномиальный, 62
гармонический, 9
Дирихле, 23
знакопеременный, 24
знакочередующийся, 26
из членов геометрической прогрессии, 5
мажорируемый, 35
мажорирующий, 36
Маклорена, 54
расходящийся, 5
с неотрицательными членами, 11
степенной, 43
сходящийся, 5
Тейлора, 54
тригонометрический, 70
условно сходящийся, 28
функциональный, 32
функциональный равномерно сходящийся, 35
Фурье, 72
числовой действительный, 5
числовой комплексный, 5
Ряды
применение степенных рядов, 64
С
Свойства сходящихся рядов, 9
Сумма
ряда, 5
функционального ряда, 33
частичная, 5
Сходимость
абсолютная функционального ряда, 32
функционального ряда в точке, 32
функционального ряда на множестве, 32
Т
Теорема
Абеля, 44
достаточное условие разложимости в ряд Тейлора, 57
достаточное условие сходимости знакопеременного ряда, 24
необходимое и достаточное условие разложимости в ряд Тейлора, 56
о дифференцировании степенных рядов, 53
о единственности разложения функции в степенной ряд, 55
о непрерывности суммы ряда, 38
о почленном дифференцировании ряда, 41
о почленном интегрировании ряда, 39
об интегрировании степенных рядов, 52
Римана, 29
Тригонометрическая система функций, 70
Ф
Функция
кусочно-монотонная, 73
Ц
Центр степенного ряда, 43
Ч
Член
функционального ряда, 32
ОТВЕТЫ
1. 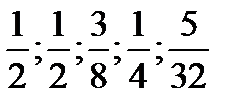 . 2.
. 2. 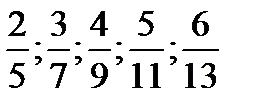 . 3.
. 3. 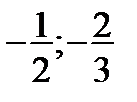 . 4.
. 4. 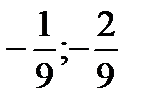 . 5.
. 5.  . 6.
. 6. 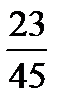 . 7.
. 7. ![]()
|
|
|



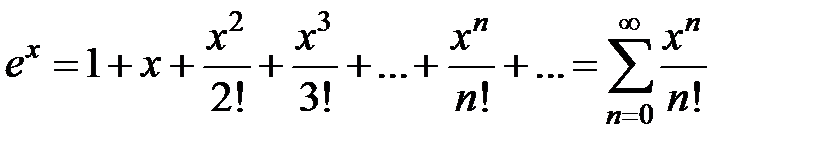 , x Î R.
, x Î R.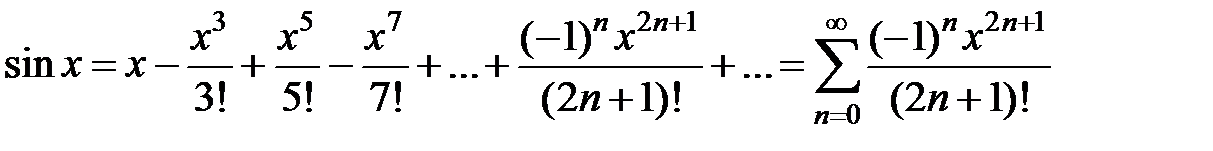 , x Î R
, x Î R , x Î R
, x Î R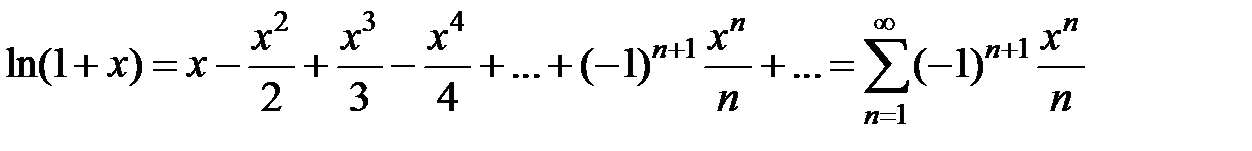 , x Î (−1;1].
, x Î (−1;1].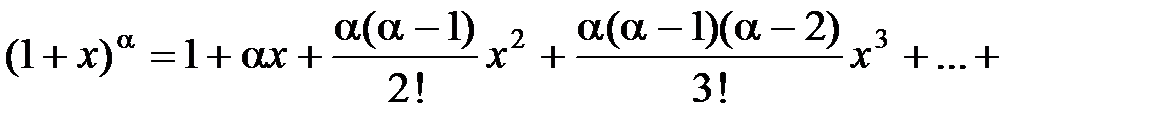
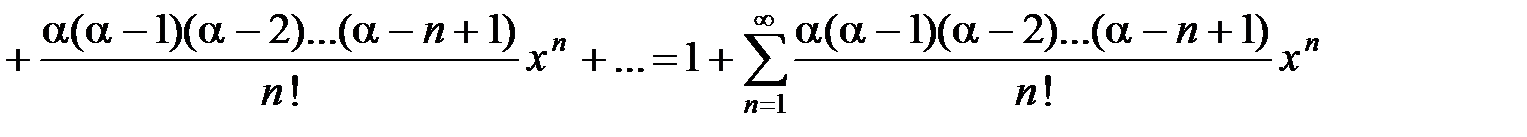 , x Î (−1;1).
, x Î (−1;1). в ряд по степеням x.
в ряд по степеням x.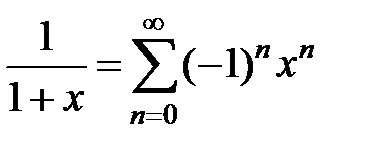 . (36)
. (36)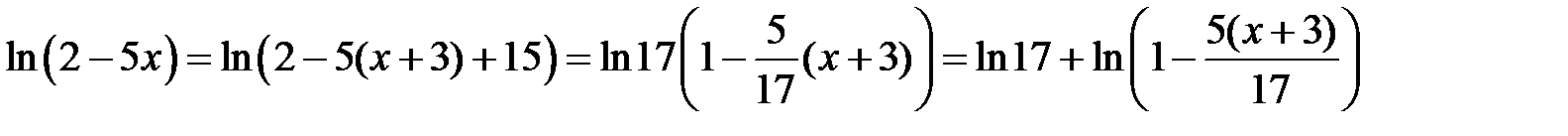 .
.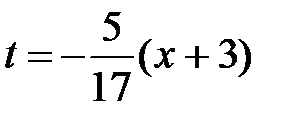 . Так как разложение (34) имеет место при x Î (–1;1], то наше разложение будет иметь место при
. Так как разложение (34) имеет место при x Î (–1;1], то наше разложение будет иметь место при 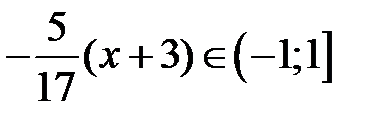 . Таким образом,
. Таким образом, 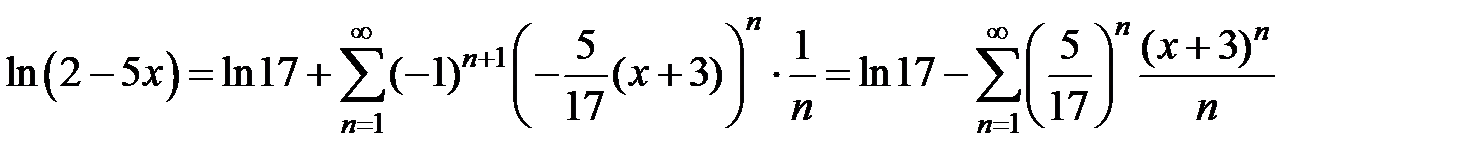 ,
,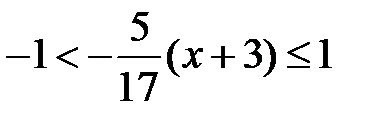 , т.е. ряд сходится при
, т.е. ряд сходится при 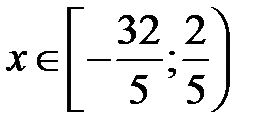 .4
.4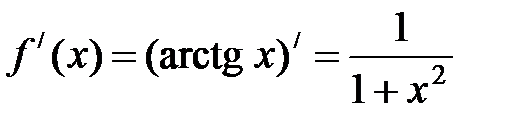 .
.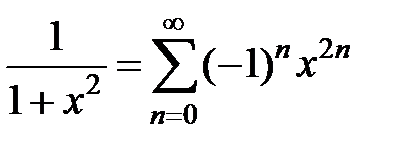 для x Î (–1;1).
для x Î (–1;1).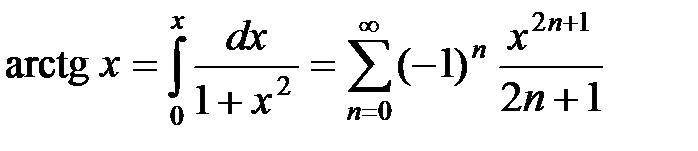 .
.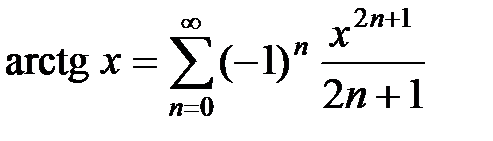 для любого x Î (–1;1].4
для любого x Î (–1;1].4 и указать области сходимости полученных рядов.
и указать области сходимости полученных рядов. .
.
 .
.
 .
.
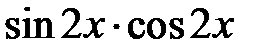 .
.
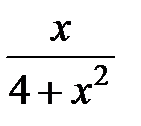 .
.
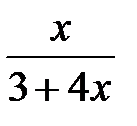 .
.
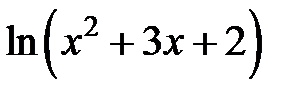 .
.
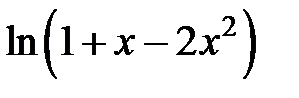 .
.
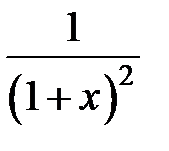 .
.
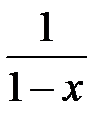 .
.
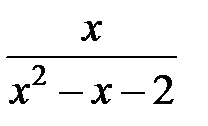 .
.
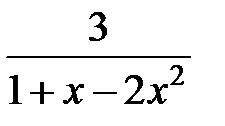 .
.
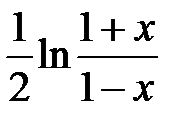 .
.
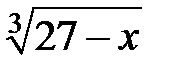 .
.
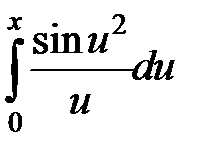 .
.
 .
.
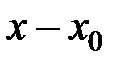 и определить области сходимости полученных рядов.
и определить области сходимости полученных рядов.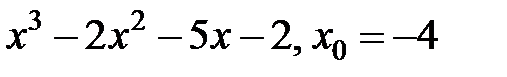 .
.
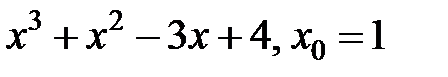 .
.
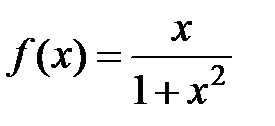 и из полученного ряда почленным дифференцированием получить ряд Маклорена для функции
и из полученного ряда почленным дифференцированием получить ряд Маклорена для функции 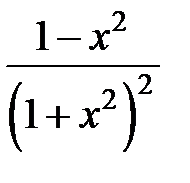 .
.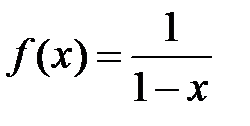 и из полученного ряда почленным дифференцированием получить ряд Маклорена для функции
и из полученного ряда почленным дифференцированием получить ряд Маклорена для функции  .
.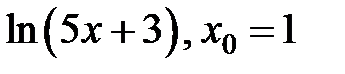 .
.
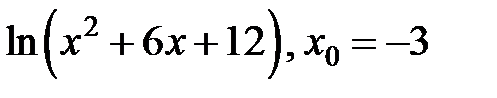 .
.
 .
.
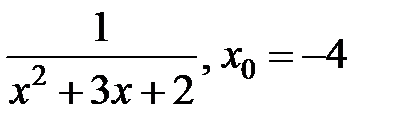 .
.
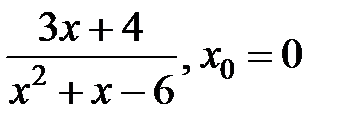 .
.
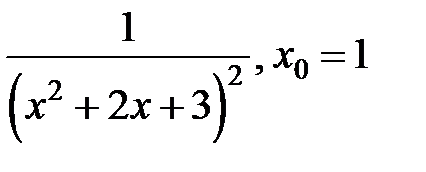 .
.
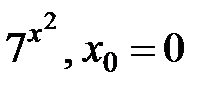 .
.
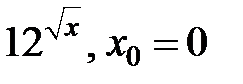 .
.
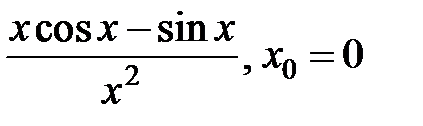 .
.
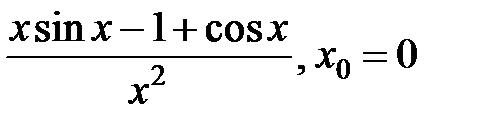 .
.
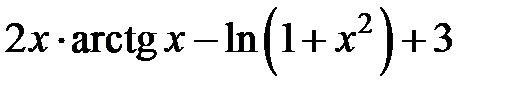 .
.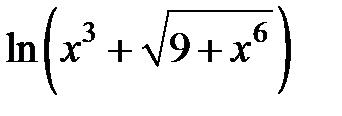 .
. , то в качестве приближенного значения функции f (x) в точке x Î (x 0– R; x 0+ R) можно взять частичную сумму этого ряда:
, то в качестве приближенного значения функции f (x) в точке x Î (x 0– R; x 0+ R) можно взять частичную сумму этого ряда: 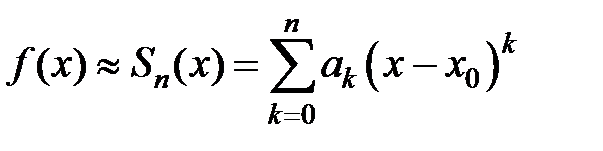 . Точность этого равенства увеличивается с ростом n. Абсолютная погрешность этого приближенного равенства равна модулю остатка ряда, т.е.
. Точность этого равенства увеличивается с ростом n. Абсолютная погрешность этого приближенного равенства равна модулю остатка ряда, т.е.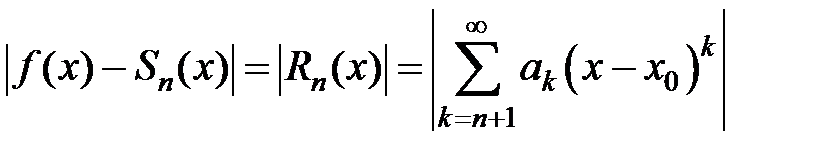 .
.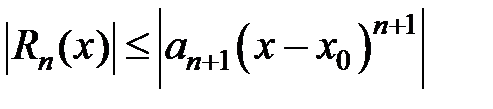 .
.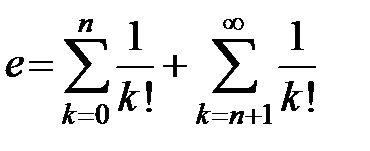 .
.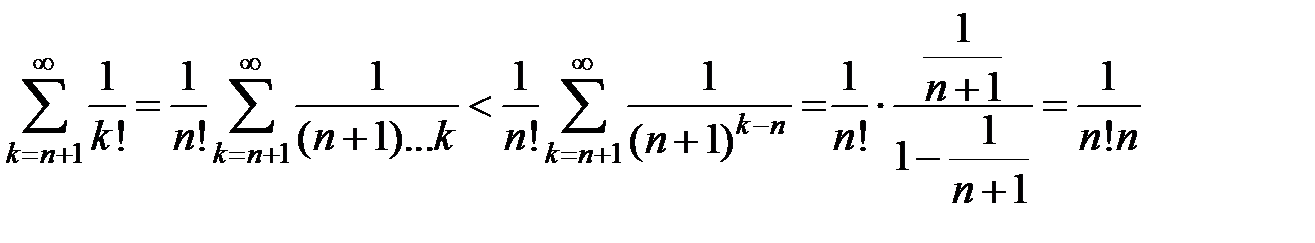 .
.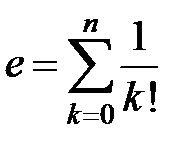 имеет абсолютную погрешность, равную
имеет абсолютную погрешность, равную 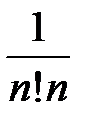 . Найдем n, для которого
. Найдем n, для которого 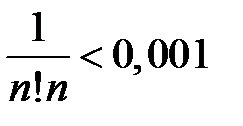 или n! n > 1000. Получаем n ³ 6. Вычисляя
или n! n > 1000. Получаем n ³ 6. Вычисляя 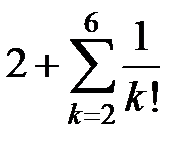 и округляя, находим ответ с требуемой точностью e» 2,718.4
и округляя, находим ответ с требуемой точностью e» 2,718.4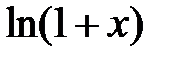 , чтобы вычислить
, чтобы вычислить  с точностью до
с точностью до 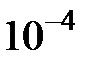 .
.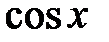 , чтобы вычислить
, чтобы вычислить 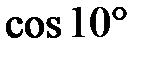 с точностью до
с точностью до 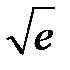 .
.
 .
.
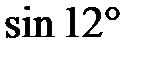 .
.
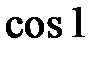 .
.
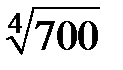 .
.
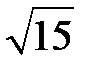 .
.

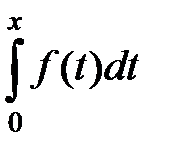 в виде степенного ряда и подсчитать величину этого интеграла с заданной точностью при любом значении
в виде степенного ряда и подсчитать величину этого интеграла с заданной точностью при любом значении 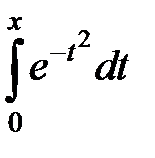 в степенной ряд по степеням x.
в степенной ряд по степеням x.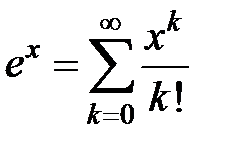 , получим
, получим 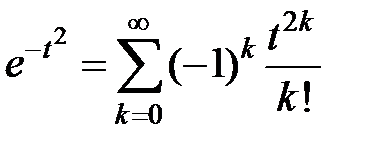 на всей числовой оси. Применяя почленное интегрирование, находим
на всей числовой оси. Применяя почленное интегрирование, находим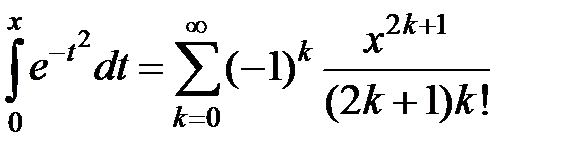 .4
.4 с точностью до 0,001.
с точностью до 0,001.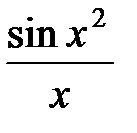 не выражается через элементарные функции. Разложим подынтегральную функцию в степенной ряд, используя разложение (31):
не выражается через элементарные функции. Разложим подынтегральную функцию в степенной ряд, используя разложение (31):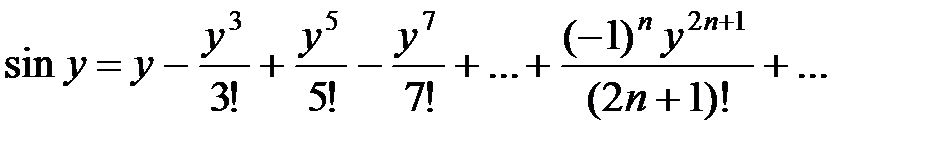
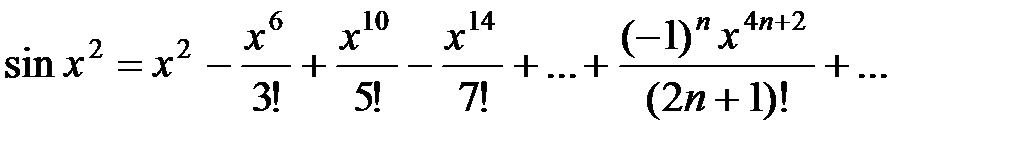
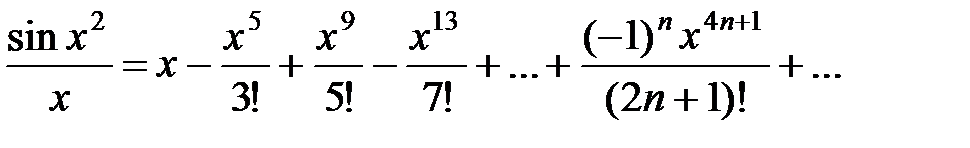
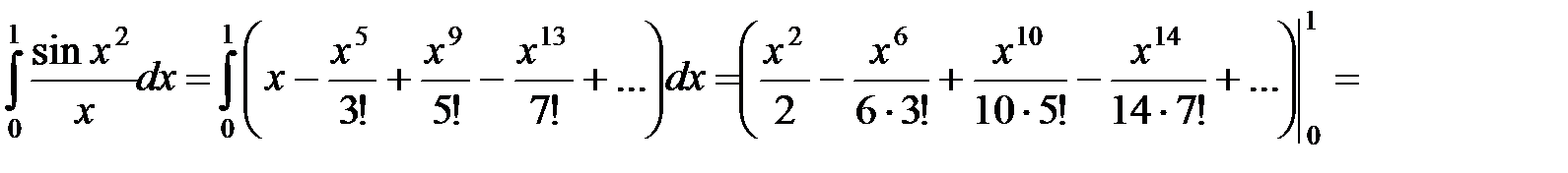
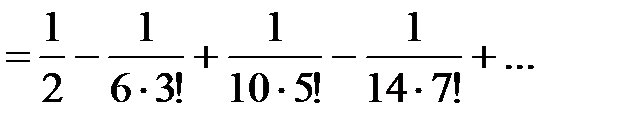
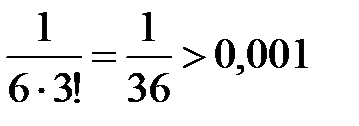 , а
, а 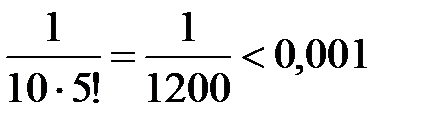 , то с точностью до 0,001 имеем
, то с точностью до 0,001 имеем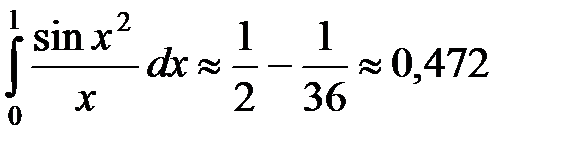 .
.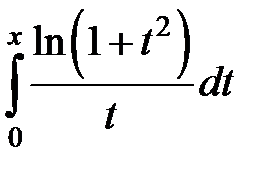 .
.
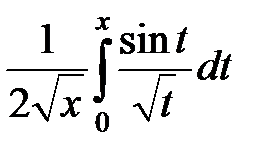 .
.
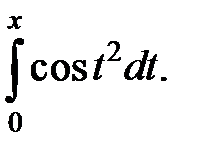
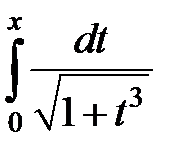
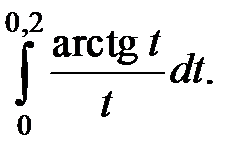
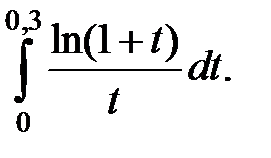
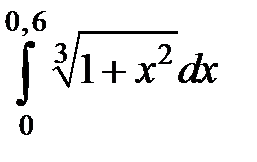 .
.
 .
.
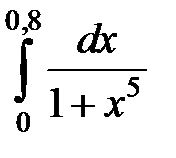 .
.
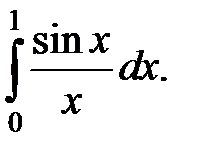
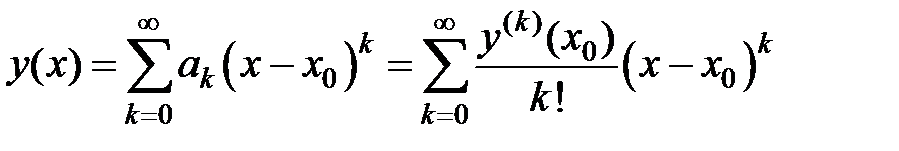 , (18)
, (18)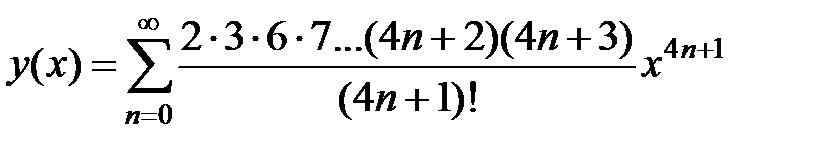 .
.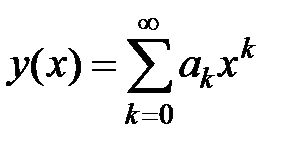 , в котором в силу условий y (0) = y /(0) = 0 имеем a 0= a 1= 0. Следовательно,
, в котором в силу условий y (0) = y /(0) = 0 имеем a 0= a 1= 0. Следовательно, 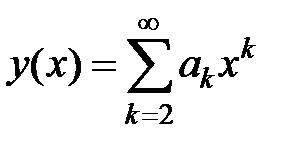 . Подставив это выражение в уравнение, получаем
. Подставив это выражение в уравнение, получаем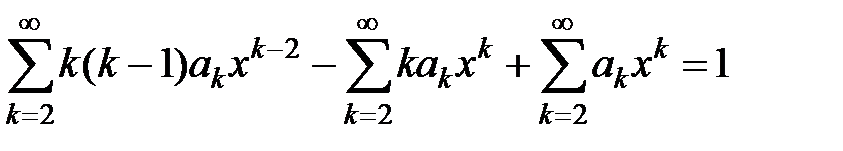 .
.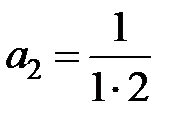 , и (k + 1)(k + 2) ak +2= =(k – 1) ak для k = 1, 2,… Так как a 1= 0, то a 2 m +1= 0 для всех m = 0, 1,…, а для k = 2 m, m = 1, 2,…, получаем рекуррентную формулу
, и (k + 1)(k + 2) ak +2= =(k – 1) ak для k = 1, 2,… Так как a 1= 0, то a 2 m +1= 0 для всех m = 0, 1,…, а для k = 2 m, m = 1, 2,…, получаем рекуррентную формулу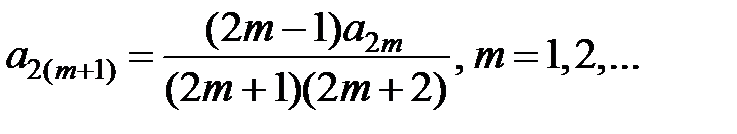 ,
,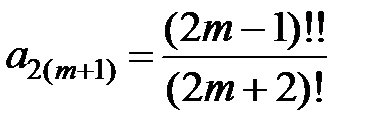 .
.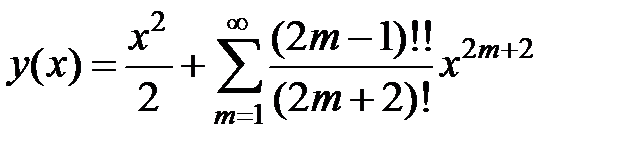 ,
, .
.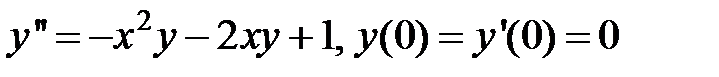 .
.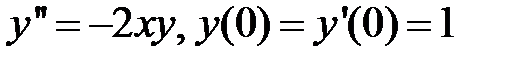 .
.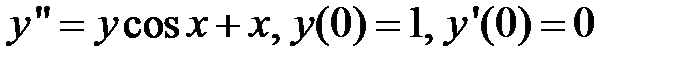 .
.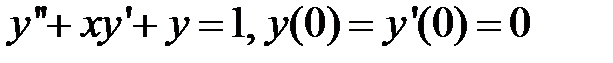 .
.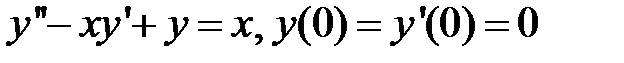 .
.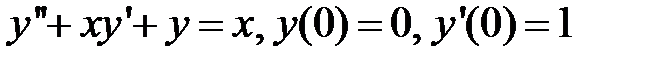 .
.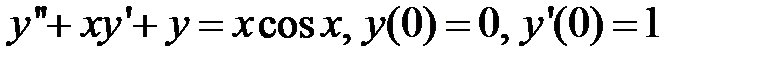 .
. (1)
(1)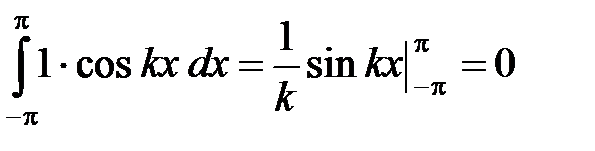 ,
, 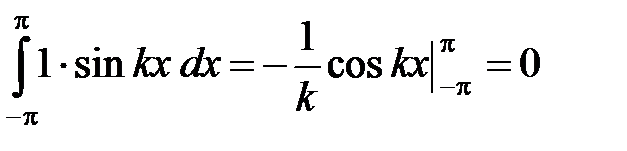 , (3)
, (3)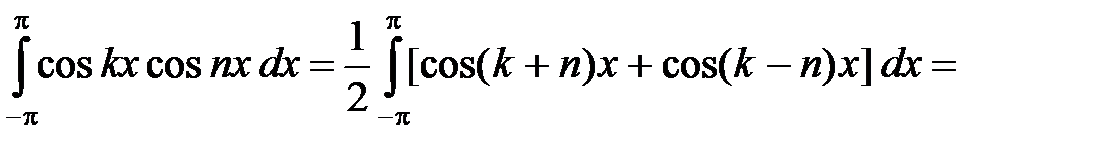
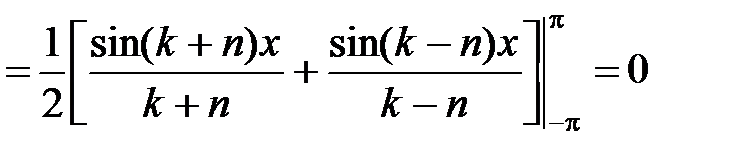 . (4)
. (4)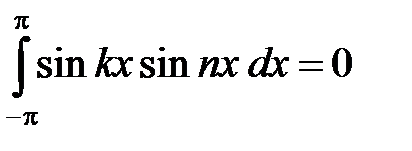 и
и 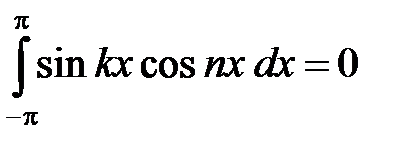 . (5)
. (5) ,
, , (6)
, (6) . ■
. ■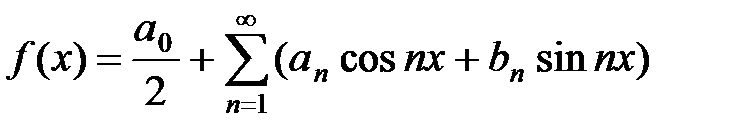 , (7)
, (7) ,
,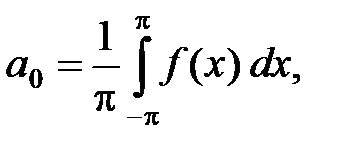 (8)
(8)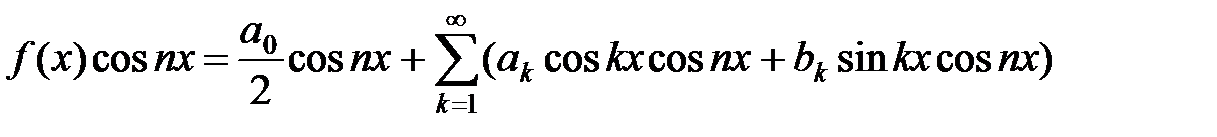 . (9)
. (9)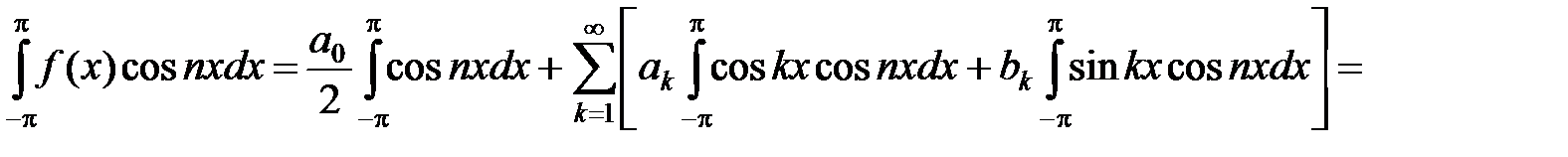
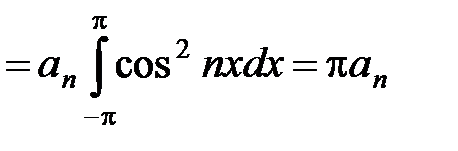 , откуда
, откуда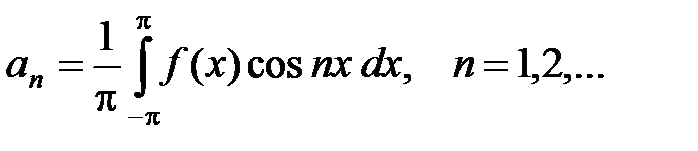 (10)
(10)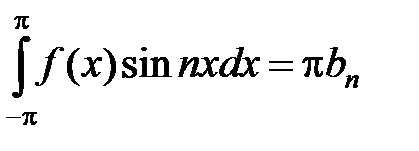 , откуда находим
, откуда находим (11)
(11)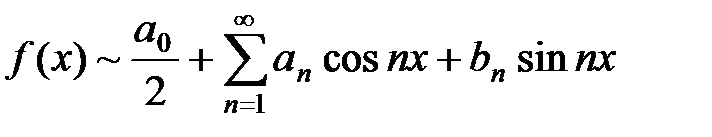
 в точках разрыва.
в точках разрыва.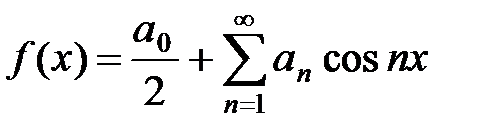 , (12)
, (12) ,
, 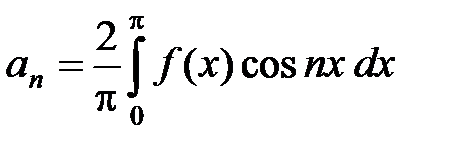 , n Î N,
, n Î N,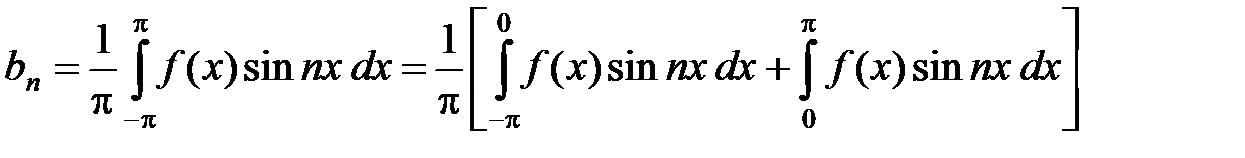 .
.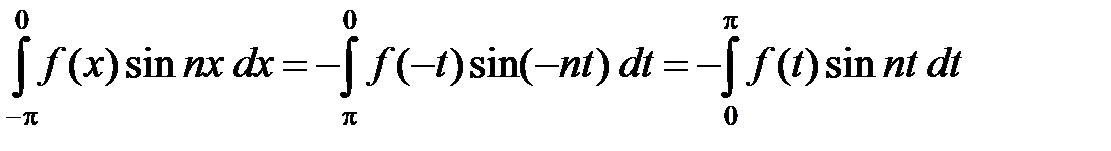 .
. .
.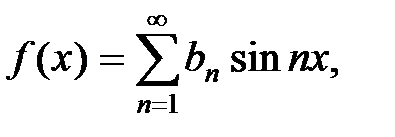
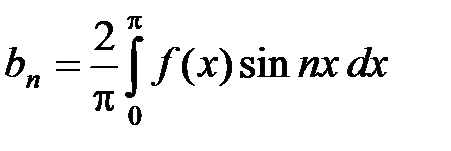 , n Î N, (13)
, n Î N, (13)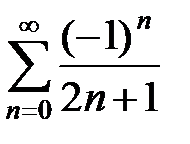 .
.
 , график которой изображен на рисунке. Эта функция 2p-периодическая, кусочно-монотонная и ограниченная, значит, согласно признаку Дирихле она разложима в ряд Фурье. Вычислим коэффициенты Фурье функции f (x). Так как функция нечетная, то an = 0, n = 0,1,…, а коэффициенты bn находится по формуле (13):
, график которой изображен на рисунке. Эта функция 2p-периодическая, кусочно-монотонная и ограниченная, значит, согласно признаку Дирихле она разложима в ряд Фурье. Вычислим коэффициенты Фурье функции f (x). Так как функция нечетная, то an = 0, n = 0,1,…, а коэффициенты bn находится по формуле (13):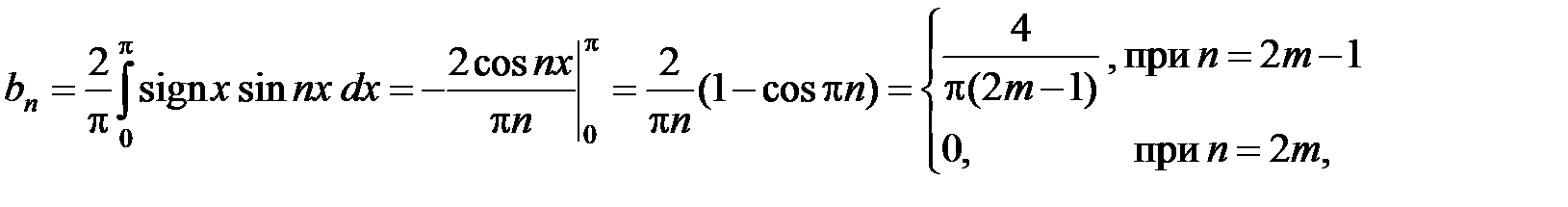
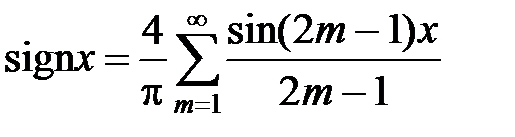 ,
,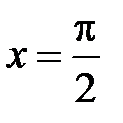 получаем
получаем 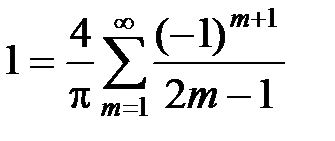 , т.е.
, т.е. 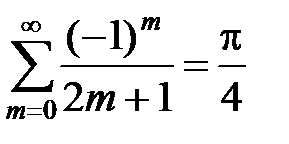 .
.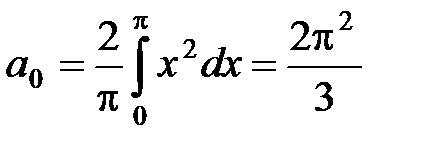 ,
, .
.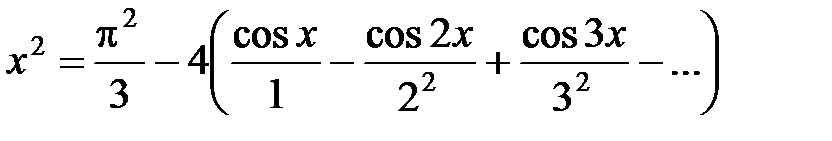 .
. .
.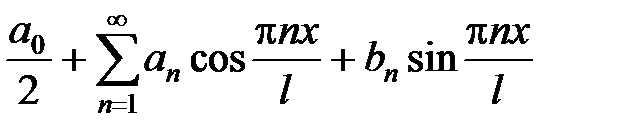 , (14)
, (14)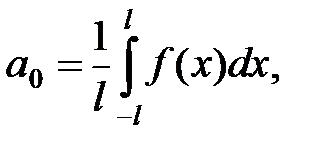
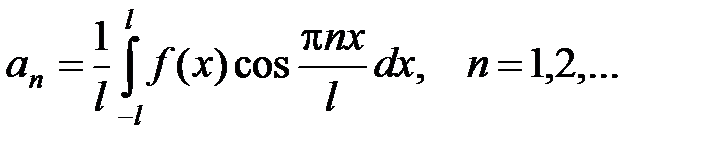 ,
,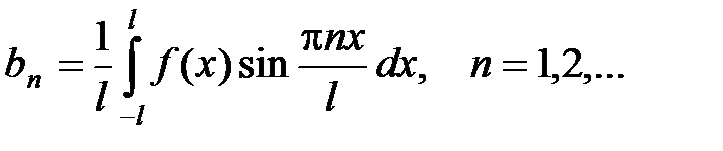
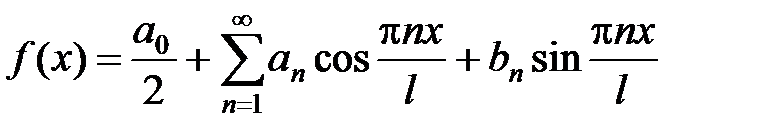 .
. . Тогда функция
. Тогда функция 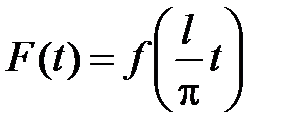 будет периодической функцией аргумента t с периодом 2p, так как
будет периодической функцией аргумента t с периодом 2p, так как ,
,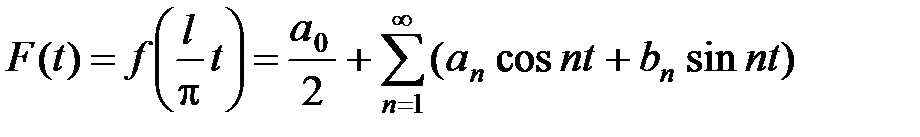 ,
,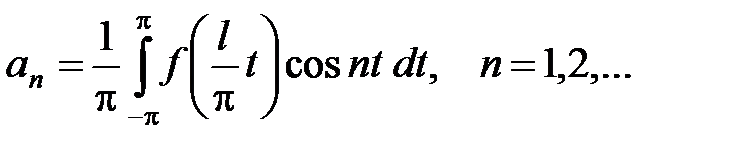

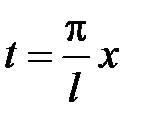 ,
, 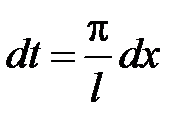 , получим ряд (14) с соответствующими коэффициентами.
, получим ряд (14) с соответствующими коэффициентами.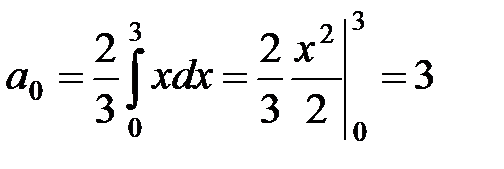 ,
,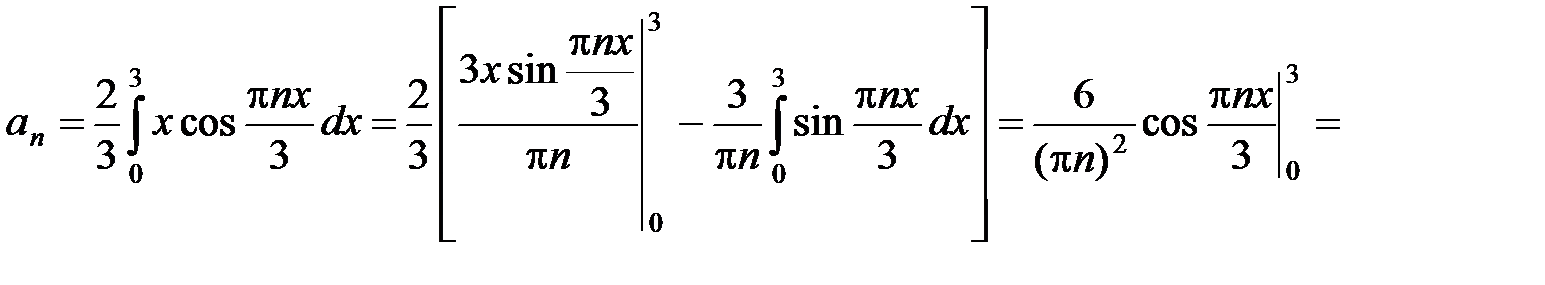
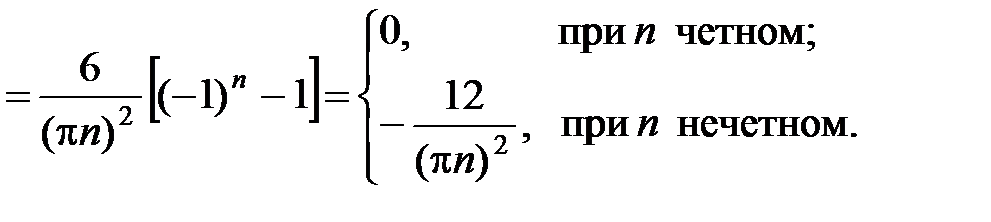
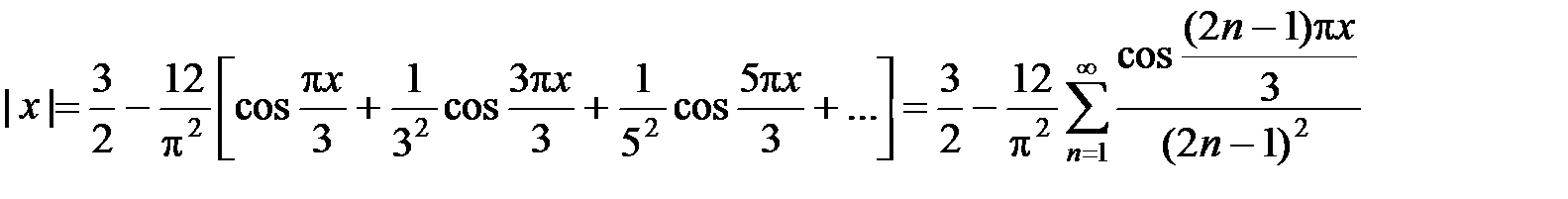 .
.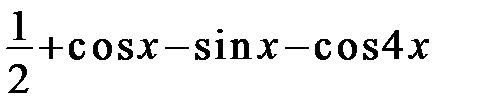 совпадает с этим многочленом.
совпадает с этим многочленом.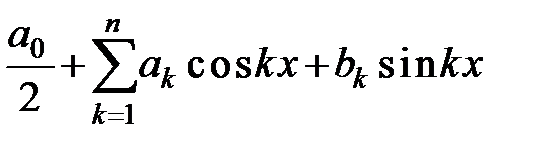 совпадает с этим многочленом.
совпадает с этим многочленом.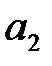 Фурье функции
Фурье функции 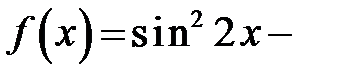
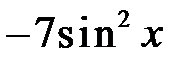 .
.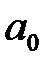 Фурье функции
Фурье функции 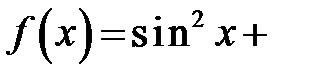
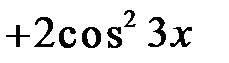 .
.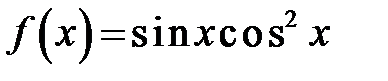 .
. .
.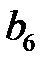 Фурье периодической с периодом
Фурье периодической с периодом 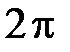 функции
функции 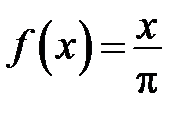 ,
, 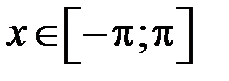 .
.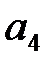 Фурье периодической с периодом
Фурье периодической с периодом  ,
, 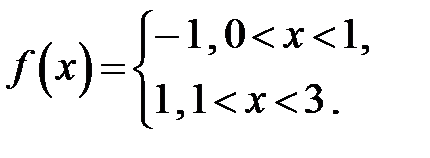
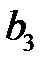 Фурье периодической с периодом 2 функции
Фурье периодической с периодом 2 функции 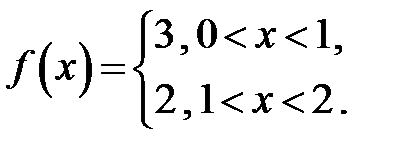
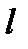 , то
, то 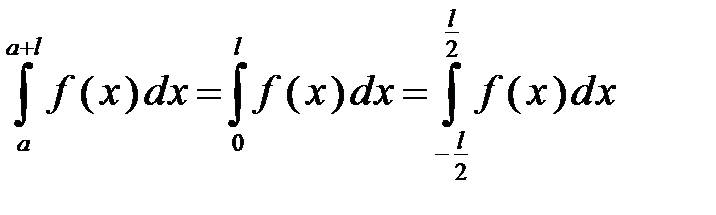 при любом
при любом 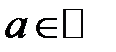 .
. .
.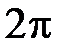 - периодичную функцию в ряд Фурье и найти значение
- периодичную функцию в ряд Фурье и найти значение 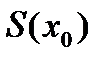 суммы полученного ряда в заданной точке
суммы полученного ряда в заданной точке 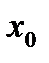 .
.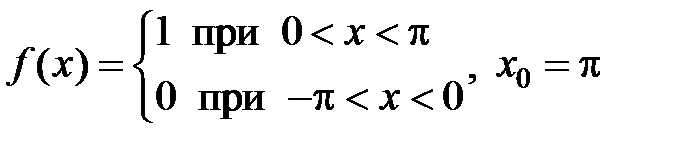 .
.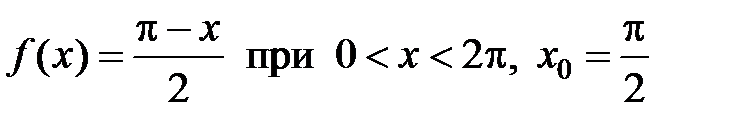 .
.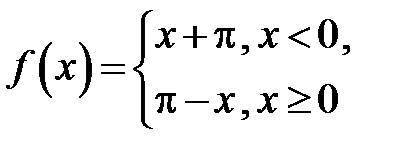 в промежутке
в промежутке 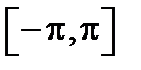 и построить график суммы ряда Фурье этой функции.
и построить график суммы ряда Фурье этой функции.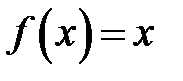 в интервале
в интервале 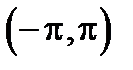 и построить график суммы ряда Фурье этой функции.
и построить график суммы ряда Фурье этой функции.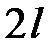 :
: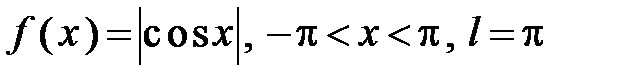 .
.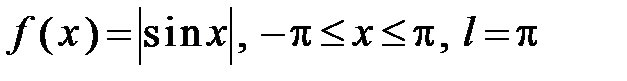 .
.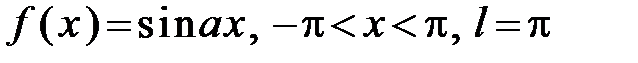 .
.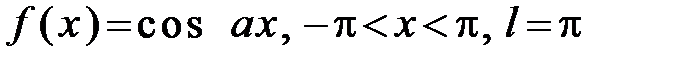 .
.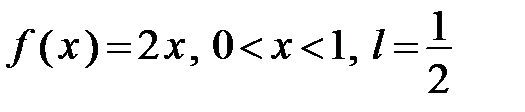 .
.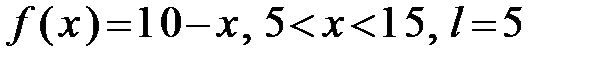 .
.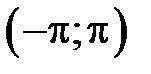 функцию
функцию 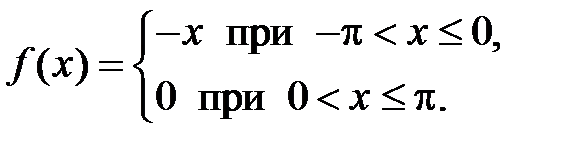
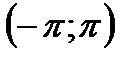 функцию
функцию 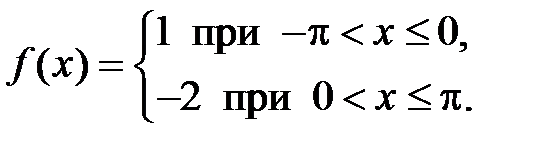
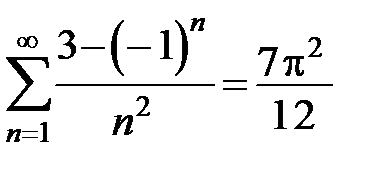 , используя разложение в ряд Фурье функции
, используя разложение в ряд Фурье функции 
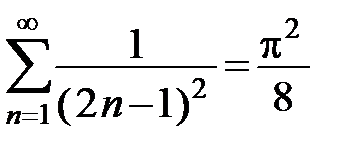 , используя разложение в ряд Фурье функции
, используя разложение в ряд Фурье функции 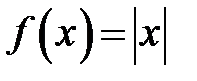 ,
, 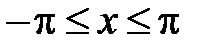 .
.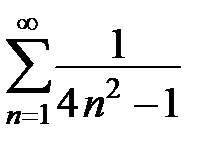 .
.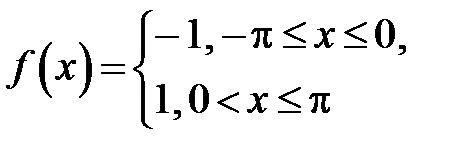 в ряд Фурье, найти сумму ряда
в ряд Фурье, найти сумму ряда 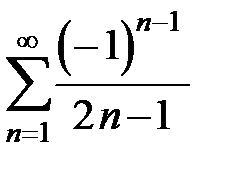 .
.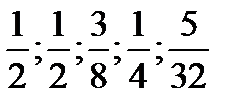 . 2.
. 2. 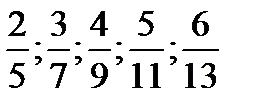 . 3.
. 3. 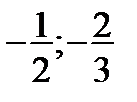 . 4.
. 4. 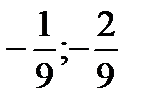 . 5.
. 5.  . 6.
. 6. 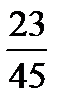 . 7.
. 7. 


