4.1. Область сходимости функционального ряда
Определение. Пусть действительные или комплексные функции fn (x), n Î N, определены на множестве D, где D – множество действительных или комплексных чисел. Выражение
 (1)
(1)
называется функциональным рядом, а функции f 1(x), f 2(x),…, fn (x),…– членами этого функционального ряда.
Определение. Если для x 0 Î D числовой ряд  сходится,то говорят, что функциональный ряд (1) сходится в точке x 0.
сходится,то говорят, что функциональный ряд (1) сходится в точке x 0.
Определение. Если в каждой точке x 0 Î D 1 Ì D числовые ряды  сходятся, то ряд (1) называется сходящимся на множестве D 1.
сходятся, то ряд (1) называется сходящимся на множестве D 1.
Определение. Функциональный ряд  называется абсолютно сходящимся на множестве D, если на множестве D сходится функциональный ряд
называется абсолютно сходящимся на множестве D, если на множестве D сходится функциональный ряд 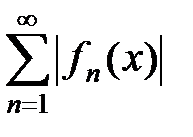 из модулей его членов.
из модулей его членов.
Определение. Множество D 0 Ì D всех точек x из D, в которых функциональный ряд  сходится, называется областью сходимости этого ряда, а область сходимости ряда
сходится, называется областью сходимости этого ряда, а область сходимости ряда 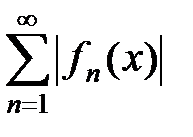 называют областью абсолютной сходимости ряда
называют областью абсолютной сходимости ряда  .
.
Определение. Функция  называется суммой, а разность
называется суммой, а разность 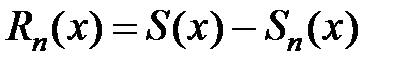 – остатком ряда.
– остатком ряда.
Для определения области абсолютной сходимости функционального ряда (1) следует воспользоваться либо признаком Даламбера, либо признаком Коши. Именно, если
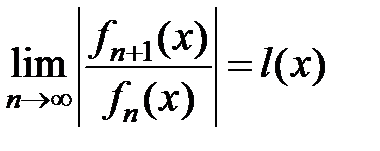 или
или  , то
, то
при l (x) < 1 ряд (1) сходится абсолютно,
при l (x) > 1 ряд (1) расходится,
при l (x) = 1 требуются дополнительные исследования.
Пример 1. Найти область сходимости функционального ряда  , x Î R, x > -3.
, x Î R, x > -3.
3Так как  и x > -3, то, применяя признак Коши, имеем
и x > -3, то, применяя признак Коши, имеем 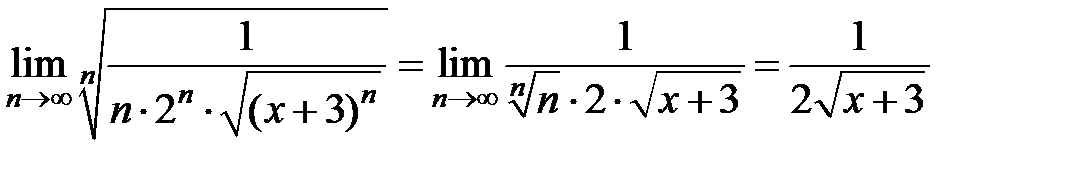 .
.
Следовательно, ряд сходится абсолютно, если  , т.е. при
, т.е. при  . Ряд расходится, если
. Ряд расходится, если 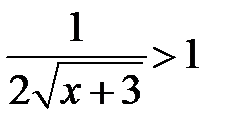 , т.е. при
, т.е. при  .
.
При  получаем знакочередующийся ряд
получаем знакочередующийся ряд  , который сходится по признаку Лейбница. Таким образом, область сходимости ряда – полуинтервал
, который сходится по признаку Лейбница. Таким образом, область сходимости ряда – полуинтервал  .4
.4
Пример 2. Найти область сходимости и абсолютной сходимости функционального ряда  .
.
3Выпишем n -й член ряда  .
.
Сначала найдем общую область определения функций fn (x). Ясно, что  , где n Î N, k Î Z, т.е. x ¹ 2 n –1p(2 k + 1).
, где n Î N, k Î Z, т.е. x ¹ 2 n –1p(2 k + 1).
Применим признак Даламбера:

 при 1 < x < 5.
при 1 < x < 5.
Учитывая область определения ряда, исключаем x = p. Таким образом, ряд сходится абсолютно при x Î (1;p) U (p;5).
Ряд расходится, если  , т.е. при x > 5 либо x < 1.
, т.е. при x > 5 либо x < 1.
 при x 1 = 1 и x 2 = 5.
при x 1 = 1 и x 2 = 5.
В точках x 1 = 1 и x 2 = 5 проводим дополнительные исследования:  .
.
Так как  , то не выполняется необходимое условие сходимости числового ряда, значит, ряд
, то не выполняется необходимое условие сходимости числового ряда, значит, ряд  расходится. Аналогично доказывается расходимость ряда
расходится. Аналогично доказывается расходимость ряда  . Итак, области сходимости и абсолютной сходимости ряда совпадают с множеством D 1 Î (1;p) U (p;5).4
. Итак, области сходимости и абсолютной сходимости ряда совпадают с множеством D 1 Î (1;p) U (p;5).4
Найти области сходимости рядов  . Исследовать ряды на абсолютную сходимость.
. Исследовать ряды на абсолютную сходимость.
165.  . .
| 166. 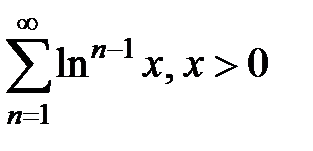 . .
|
167.  . .
| 168.  . .
|
169.  . .
| 170.  . .
|
171.  . .
| 172.  . .
|
173. 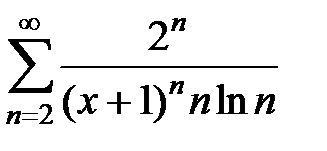 . .
| 174.  . .
|
Найти области абсолютной сходимости рядов  :
:
175.  . .
| 176.  . .
|
177.  . .
| 178.  . .
|
4.2. Равномерная сходимость. Мажорируемый ряд
Определение. Сходящийся в области D 1 функциональный ряд 
 называется равномерно сходящимся к функции f (x) в этой области, если для любого e > 0 найдется N = N (e) такое, что при всех n ≥ N (e) и x Î D 1
называется равномерно сходящимся к функции f (x) в этой области, если для любого e > 0 найдется N = N (e) такое, что при всех n ≥ N (e) и x Î D 1
 .
.
Определение. Функциональный ряд

называется мажорируемым в области D 1, если существует такой сходящийся числовой ряд

с положительными членами, что " x Î D 1выполняются соотношения:
| f 1(x)| £ a 1, | f 2(x)| £ a 2,…, | fn (x)| £ an,…
Теорема (признак Вейерштрасса равномерной сходимости функционального ряда). Пусть функции fn (x), n Î N определены в области D 1, и пусть существует числовой ряд  такой, что:
такой, что:
1) " n ³ n 0 " x Î D 1: | fn (x)| £ an;
2) ряд  сходится.
сходится.
Тогда функциональный ряд 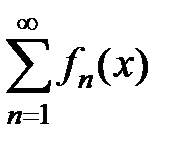 сходится абсолютно и равномерно в области D 1.
сходится абсолютно и равномерно в области D 1.
Числовой ряд  называется мажорирующим для функционального ряда
называется мажорирующим для функционального ряда 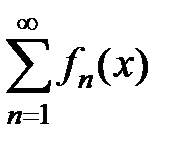 .
.
Из теоремы Вейерштрасса следует, что мажорируемый ряд является равномерно сходящимся.
Пример 3. Исследовать на абсолютную и равномерную сходимость ряд  , x Î R.
, x Î R.
3Ряд  сходится равномерно и абсолютно при всех x Î R, поскольку для него существует мажорирующий сходящийся числовой ряд
сходится равномерно и абсолютно при всех x Î R, поскольку для него существует мажорирующий сходящийся числовой ряд  , так как
, так как  при x Î R.4
при x Î R.4
Пример 4. Исследовать на абсолютную и равномерную сходимость ряд 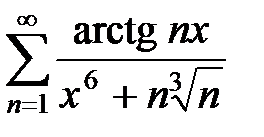 , x Î R.
, x Î R.
3Так как для всех x Î R: 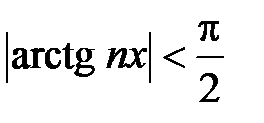 , то " x Î R и " n Î N имеем
, то " x Î R и " n Î N имеем  . Из сходимости мажорирующего ряда
. Из сходимости мажорирующего ряда  следует абсолютная и равномерная сходимость ряда
следует абсолютная и равномерная сходимость ряда 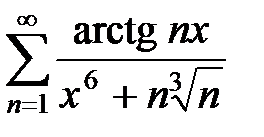 на R.4
на R.4
4.3. Непрерывность суммы ряда
Пусть дан ряд из непрерывных функций
 ,
,
сходящийся на некотором отрезке [ a, b ]. Известно, что сумма конечного числа непрерывных функций есть функция непрерывная. Для суммы ряда (состоящего из бесконечного числа слагаемых) это свойство не сохраняется. Некоторые функциональные ряды с непрерывными членами имеют в качестве суммы непрерывную функцию, у других функциональных рядов с непрерывными членами сумма является разрывной функцией.
Пример 5. Доказать, что ряд

сходится, а его сумма – разрывная функция.
3Члены этого ряда – непрерывные функции для любого x. Очевидно, что n -я частичная сумма ряда  . Покажем, что в точке х = 0 сумма ряда имеет разрыв.
. Покажем, что в точке х = 0 сумма ряда имеет разрыв.
Пусть x > 0, тогда
 .
.
Пусть x < 0, тогда
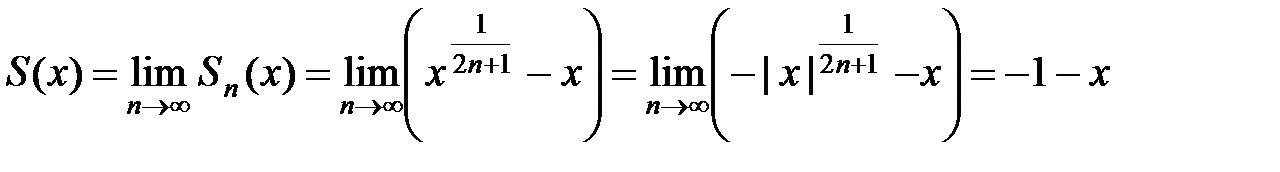 .
.
Пусть х = 0, тогда Sn (x) = 0 и  .
.
Таким образом, для любого х ряд сходится, а в точке х = 0 сумма ряда имеет разрыв.4
Теорема (о непрерывности). Сумма ряда непрерывных функций, мажорируемого на некотором отрезке [ a, b ], есть функция, непрерывная на этом отрезке.
Доказательство. Пусть имеем мажорируемый на отрезке [ a, b ] ряд непрерывных функций
 .
.
Представим его сумму в виде
S (x) = Sn (x) + rn (x),
где Sn (x) = f 1(x) +…+ fn (x), а rn (x) = fn+ 1(x) + fn+ 2(x)+…
Возьмем на отрезке [ a, b ] произвольное значение аргумента x и придадим ему такое приращение D x, чтобы точка x + D x лежала тоже на отрезке [ a, b ].
Введем обозначения:
D S = S (x + D x) – S (x), D Sn = Sn (x + D x) – Sn (x),
тогда D S = D Sn + rn (x + D x) – rn (x), откуда
|D S| = |D Sn| + | rn (x + D x)| + | rn (x)|. (2)
Это неравенство справедливо для любого номера n.
Чтобы доказать непрерывность S (x), нужно показать, что при любом наперед заданном и как угодно малом e > 0 найдется число d > 0 такое, что при всех |D x| < d будет |D S| < e.
Так как  – мажорируемый, то при любом наперед заданном e > 0 найдется такой номер N, что при всех n ³ N, и в частности при n = N, будет выполняться неравенство
– мажорируемый, то при любом наперед заданном e > 0 найдется такой номер N, что при всех n ³ N, и в частности при n = N, будет выполняться неравенство
| rN (x)| < e/3 (3)
при любом x из отрезка [ a, b ]. Значение x + D x лежит на отрезке [ a, b ] и потому выполняется неравенство
| rN (x + D x)| < e/3 (3/)
Далее, при выбранном N частичная сумма SN (x) есть функция непрерывная (сумма конечного числа непрерывных функций) и, следовательно, можно подобрать такое положительное число d, что для всякого D x, удовлетворяющего условию |D x| < d, выполняется неравенство
|D SN | < e/3. (4)
На основании неравенств (2), (3), (3/) и (4) получаем:
|D S | < e/3 + e/3 + e/3 = e, т.е. |D S | < e при |D x| < d, а это и означает, что S (x) является непрерывной функцией в точке x и, следовательно, в любой точке отрезка [ a, b ]. ■
4.4. Теоремы о почленном интегрировании и дифференцировании мажорируемых рядов
Теорема (о почленном интегрировании). Пусть дан ряд непрерывных функций
 ,
,
мажорируемый на отрезке [ a, b ], и пусть S (x) есть сумма этого ряда. Тогда интеграл от S (x) в пределах от a до х, [a, x ] Ì [ a, b ], равняется сумме таких же интегралов от членов данного ряда, т.е.

Доказательство. Функцию S (x) можно представить в виде
S (x) = Sn (x) + rn (x)
или S (x) = f 1(x) + f 2(x) +…+ fn (x) + rn (x). Тогда
 (5)
(5)
(т.к. интеграл от суммы конечного числа слагаемых равен сумме интегралов от этих слагаемых).
Так как исходный ряд  мажорируемый, то при любом x имеем | rn (x)| < e n, где e n ® 0 при n ® ¥. Поэтому
мажорируемый, то при любом x имеем | rn (x)| < e n, где e n ® 0 при n ® ¥. Поэтому
 .
.
Так как e n ® 0, то  . Но из равенства (5) получаем:
. Но из равенства (5) получаем:
 .
.
Следовательно,
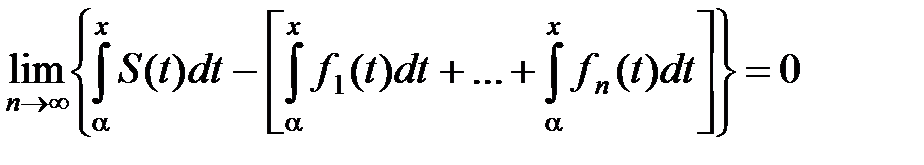 ,
,
или
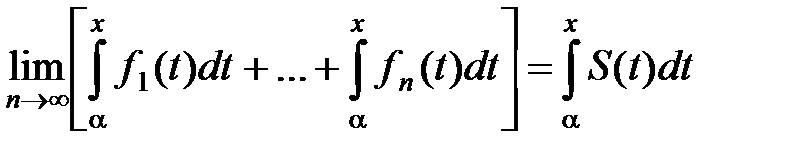 . (6)
. (6)
Сумма, стоящая в квадратных скобках, есть частичная сумма ряда
 (7)
(7)
Поскольку частичные суммы этого ряда имеют предел, этот ряд сходится и его сумма в силу равенства (6) равна  , т.е.
, т.е.
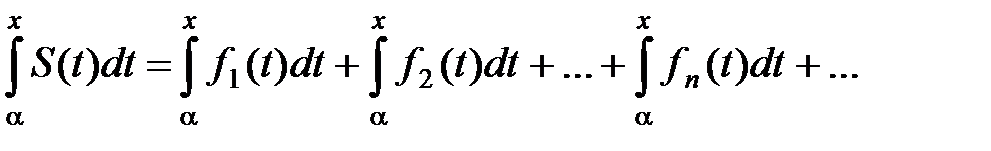 ,
,
а это и есть равенство, которое требовалось доказать. ■
Замечание. Если ряд не мажорируемый, то почленное интегрирование ряда не всегда возможно. То есть интеграл  от суммы ряда
от суммы ряда  не всегда равен сумме интегралов от его членов (т.е. сумме ряда (7)).
не всегда равен сумме интегралов от его членов (т.е. сумме ряда (7)).
Теорема (о почленном дифференцировании). Если ряд
 ,
,
составленный из функций, имеющих непрерывные производные на отрезке [ a, b ], сходится на этом отрезке к сумме S (x) = f 1(x) + f 2(x) +…+ fn (x) и ряд
 , (8)
, (8)
составленный из производных его членов мажорируемый на том же отрезке, то сумма ряда производных равна производной от суммы первоначального ряда, т.е.
 .
.
Доказательство. Обозначим через F (x) сумму ряда (8):
 ,
,
и докажем, что F (x) = S /(x). Так как ряд (8) мажорируемый, то на основании предыдущей теоремы:
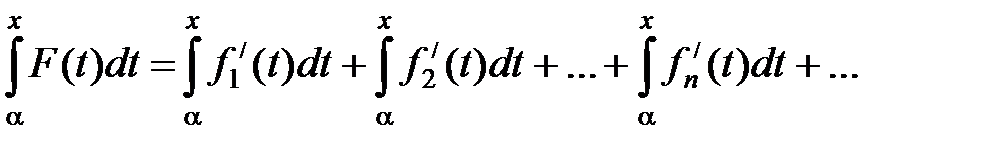
Производя интегрирование, будем иметь:

Но по условию S (x) = f 1(x) + f 2(x) +…+ fn (x) +…,
S (a) = f 1(a) + f 2(a) +…+ fn (a) +…,
каковы бы ни были числа х и a на отрезке [ a, b ]. Поэтому 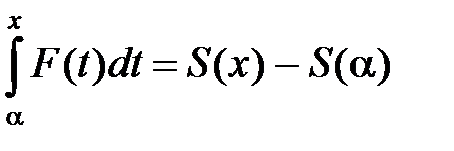 . Дифференцируя по х обе части последнего равенства, получим: F (x) = S /(x). ■
. Дифференцируя по х обе части последнего равенства, получим: F (x) = S /(x). ■
Замечание. Требование мажорируемости ряда производных является весьма существенным, и его невыполнение может привести к невозможности почленного дифференцирования ряда.
В качестве примера рассмотрим ряд:
 .
.
3Этот ряд сходится к непрерывной функции, так как он мажорируемый. Действительно, при любом х его члены по абсолютной величине меньше членов числового сходящегося ряда с положительными членами
 .
.
Напишем ряд, составленный из производных членов исходного ряда:
 .
.
В точке x = 0 этот ряд превращается в ряд
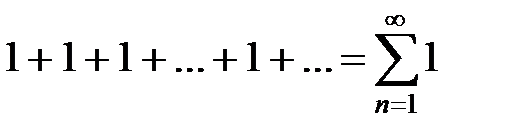 ,
,
который расходится.
Можно показать, что ряд из производных расходится не только при х = 0.
Таким образом, хотя сам рассмотренный ряд мажорируемый для всех х, однако, он не допускает почленного дифференцирования. 4
Пользуясь признаком.Вейерштрасса доказать абсолютную и равномерную сходимость рядов на множестве  .
.
179.  . .
| 180.  . .
|
181.  . .
| 182.  . .
|
183.  . .
| 184.  . .
|
Задачи повышенной сложности
Исследовать ряд на равномерную и абсолютную сходимость.
185. 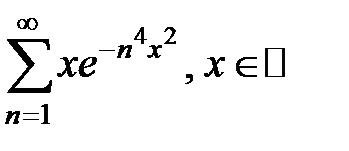 . .
| 186. 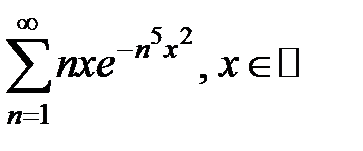 . .
|
187. Доказать, что если члены равномерно сходящегося в области 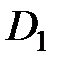 функционального ряда
функционального ряда 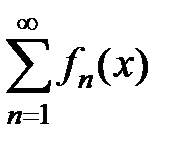 умножить на одну и ту же ограниченную в области
умножить на одну и ту же ограниченную в области 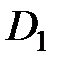 функцию
функцию 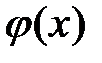 , то равномерная сходимость ряда не нарушится.
, то равномерная сходимость ряда не нарушится.
188. Доказать, что если функции 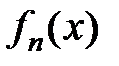 непрерывны в области
непрерывны в области 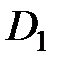 и ряд
и ряд 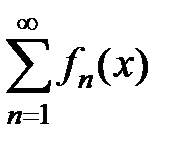 равномерно сходится в этой области, то его сумма
равномерно сходится в этой области, то его сумма 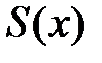 непрерывна в области
непрерывна в области 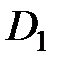 .
.
189. Определить при 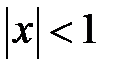 сумму и остаток ряда
сумму и остаток ряда 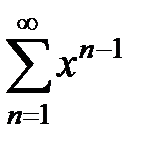 и показать, что он сходится равномерно на отрезке
и показать, что он сходится равномерно на отрезке 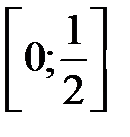 . При каком
. При каком 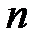 остаток
остаток 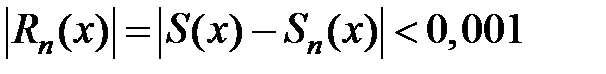 для любого
для любого 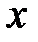 на этом отрезке?
на этом отрезке?
190. Показать, что ряд 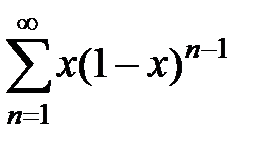 сходится неравномерно на отрезке
сходится неравномерно на отрезке 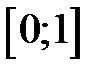 и равномерно на отрезке
и равномерно на отрезке 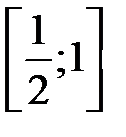 . При каком
. При каком 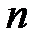 остаток
остаток 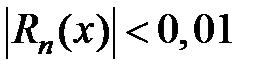 для любого
для любого 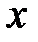 на отрезке
на отрезке 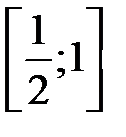 ?
?
191. Показать, что ряд 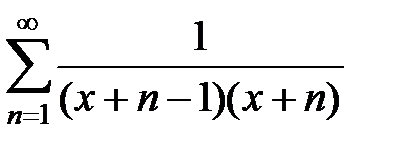 сходится равномерно к
сходится равномерно к 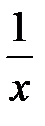 в интервале
в интервале 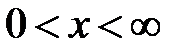 . При каком
. При каком 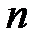 (и любом
(и любом 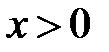 ) остаток ряда
) остаток ряда 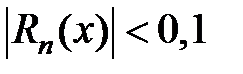 ?
?
192. Показать, что ряд 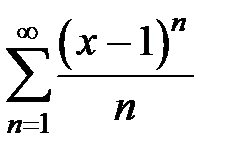 сходится равномерно на отрезке
сходится равномерно на отрезке 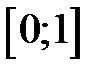 . При каких
. При каких 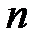 и любом
и любом 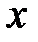 на этом отрезке
на этом отрезке 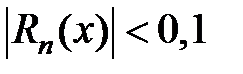 ?
?
Тема 5. Степенные ряды
5.1. Основные понятия. Теорема Абеля
Определение. Функциональный ряд вида
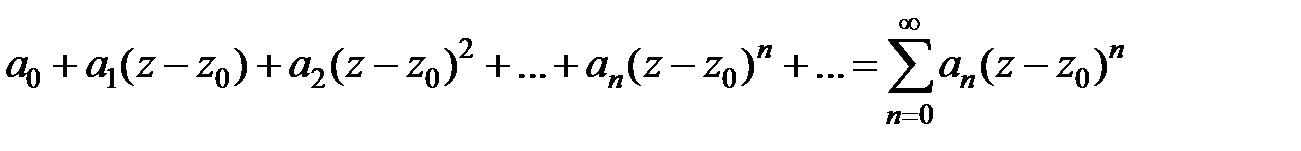 , (9)
, (9)
где an, z, z 0Î C, называется степенным рядом по степеням (z – z 0) Числа an, n = 0, 1, 2,… называются коэффициентами степенного ряда, z 0– центром степенного ряда.
В частности, ряд
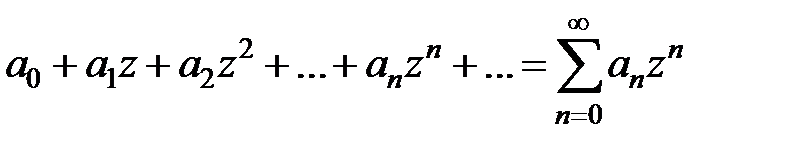 (10)
(10)
является степенным по степеням z. С помощью замены z – z 0= Z ряд (9) сводится к ряду (10).
Придавая z различные числовые значения, будем получать различные числовые ряды, которые могут оказаться сходящимися или расходящимися. Множество тех значений z, при которых ряд (10) сходится, называется областью сходимости степенного ряда. Это множество всегда не пусто, так как любой степенной ряд (10) сходится при z = 0.
Теорема 1 (Абеля). Если степенной ряд (10) сходится в точке z = z 1¹ 0, то он абсолютно сходится для всех z таких, что | z | < | z 1|. Если же ряд (10) расходится в точке z = z 2 ¹ 0, то он расходится и для всех z таких, что | z | > | z 2|.
Доказательство. а) Пусть
K 1= {
z: |
z | < |
z 1|} – круг на комплексной плоскости с центром в точке
О радиуса |
z 1|, как изображено на рисунке, и пусть
z – произвольная точка круга
K 1, т.е. |
z | < |
z 1|, и поэтому
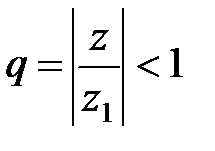 . (11)
. (11)
Так как ряд (10) по условию сходится в точке z 1, то должно выполняться условие 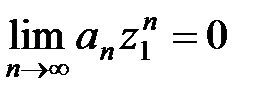 , откуда следует, что последовательность
, откуда следует, что последовательность 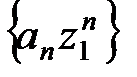 ограничена, т.е. существует число М > 0 такое, что
ограничена, т.е. существует число М > 0 такое, что
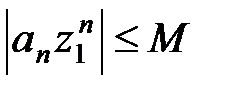 , n = 0, 1, 2,… (12)
, n = 0, 1, 2,… (12)
Используя неравенства (11) и (12), получаем:
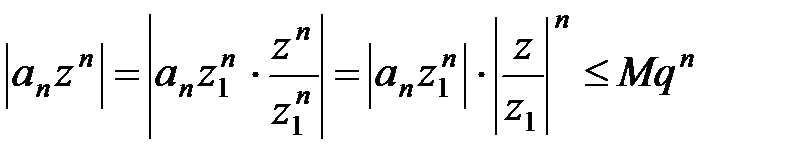 , где 0 £ q < 1. (13)
, где 0 £ q < 1. (13)
Так как ряд 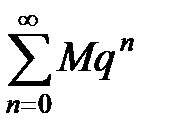 , составленный из членов геометрической прогрессии со знаменателем 0 £ q < 1, сходится, то по признаку сравнения сходится и ряд
, составленный из членов геометрической прогрессии со знаменателем 0 £ q < 1, сходится, то по признаку сравнения сходится и ряд 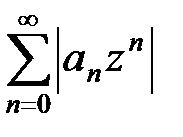 , т.е. ряд (10) сходится абсолютно в каждой точке круга K 1.
, т.е. ряд (10) сходится абсолютно в каждой точке круга K 1.
б) Пусть теперь ряд (10) расходится в точке z 2 ¹ 0. Требуется показать, что он расходится для всех z, удовлетворяющих условию | z | > | z 2|. Предположим обратное, т.е. допустим, что при некотором значении z, таком, что | z | > | z 2|, ряд (10) сходится. Тогда по только что доказанной первой части теоремы ряд (10) должен сходиться и в точке z 2. Но это противоречит тому, что в точке z 2ряд расходится. ■
5.2. Радиус и круг сходимости степенного ряда
Теорема 2. Для всякого степенного ряда (10) справедливо одно из следующих утверждений:
1) существует число R > 0, такое, что при всех z, таких, что | z | < R, ряд сходится абсолютно, а при | z | > R – расходится;
2) ряд сходится только в точке z = 0;
3) ряд сходится для всех z.
Поясним эту теорему. Пусть D – множество всех точек сходимости ряда (10). Это непустое множество, т.к. в точке z = 0 ряд (10) сходится.
Если D – неограниченное множество, то ряд (10) сходится в произвольной точке z комплексной плоскости. В самом деле, возьмем точку z 1Î D, такую, что | z | < | z 1|. Тогда по теореме Абеля ряд (10) будет сходиться в точке z (третье утверждение).
Пусть D – ограниченное множество. Может оказаться, что множество D состоит из одной точки z = 0. Тогда ряд (10) сходится только в точке z = 0 и расходится при z ¹ 0 (второе утверждение).
Пусть теперь
D содержит точку
z 1 ¹ 0. Тогда по теореме Абеля ряд (10) будет сходиться для всех
z, таких, что |
z | < |
z 1|. Если
z 2Ï
D, |
z 2| > |
z 1|, то ряд (10) будет расходиться для всех
z, таких, что |
z | > |
z 2|. Тогда существует число
R: |
z 1| <
R < |
z 2|, такое, что окружность |
z | =
R (на рисунке обозначена пунктиром) отделяет область сходимости от области расходимости, т.е. ряд сходится для всех
z, таких, что |
z | <
R и расходится для всех
z, таких, что |
z | >
R (первое утверждение).
Вопрос о сходимости ряда (10) в точках окружности | z | = R, R > 0 остается открытым и решается отдельно для каждого ряда.
Определение. Пусть задан степенной ряд 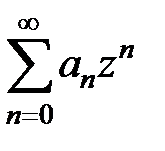 . Если R – неотрицательное число или +¥, обладает тем свойством, что при всех z, для которых | z | < R, этот ряд сходится, а при всех z, для которых | z | > R – расходится, то оно называется радиусом сходимости степенного ряда. Множество точек z, для которых | z | < R, называется – кругом сходимости ряда (в случае ряда с действительными членами интервал (– R, R) – интервалом сходимости).
. Если R – неотрицательное число или +¥, обладает тем свойством, что при всех z, для которых | z | < R, этот ряд сходится, а при всех z, для которых | z | > R – расходится, то оно называется радиусом сходимости степенного ряда. Множество точек z, для которых | z | < R, называется – кругом сходимости ряда (в случае ряда с действительными членами интервал (– R, R) – интервалом сходимости).
Так, в доказанной выше теореме в случае 2) полагают радиус сходимости R = 0, в случае 3) R = +¥.
Теорема 3. Если существует конечный или бесконечный 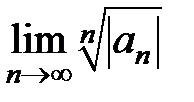 , то для радиуса R сходимости ряда (10) справедлива формула
, то для радиуса R сходимости ряда (10) справедлива формула
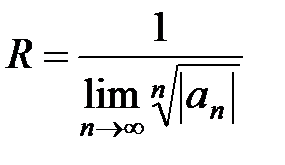 , (14)
, (14)
а если существует конечный или бесконечный 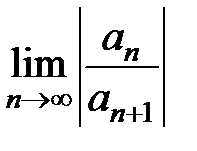 , то
, то
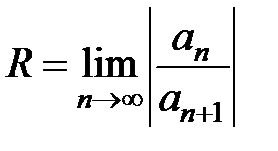 . (15)
. (15)
Доказательство. 1) Докажем сначала формулу (14). Обозначим 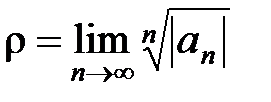 .
.
а) Пусть 0 < r < +¥ и пусть z 1– произвольная точка круга 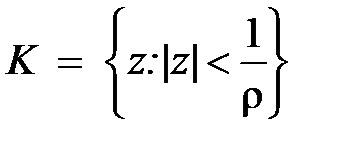 , тогда
, тогда 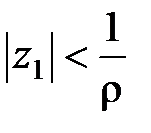 . Рассмотрим предел
. Рассмотрим предел
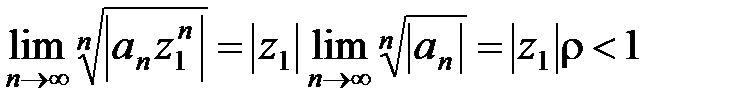 .
.
По признаку Коши (см. п.2.3) ряд 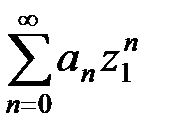 абсолютно сходится. Так как точка z 1– произвольная точка круга K, то ряд (10) абсолютно сходится в этом круге.
абсолютно сходится. Так как точка z 1– произвольная точка круга K, то ряд (10) абсолютно сходится в этом круге.
Пусть точка z 2лежит вне круга K, тогда 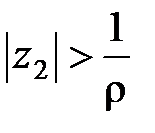 и поэтому
и поэтому
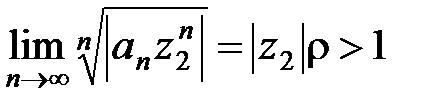 .
.
Следовательно, ряд 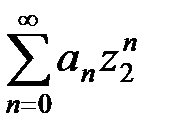 расходится при
расходится при 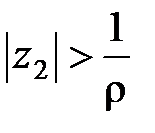 .
.
Если правая часть равенства (14) положительное число, то ряд (10) сходится в круге K и расходится вне этого круга. Значит, 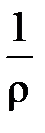 – радиус сходимости ряда (10).
– радиус сходимости ряда (10).
б) Если r= 0, то 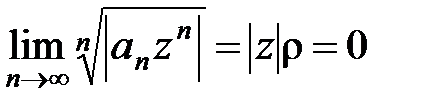 для любой точки z комплексной плоскости, и поэтому ряд (10) сходится при любом z. Это означает, что радиус сходимости ряда R = +¥ и формула (14) верна и в этом случае.
для любой точки z комплексной плоскости, и поэтому ряд (10) сходится при любом z. Это означает, что радиус сходимости ряда R = +¥ и формула (14) верна и в этом случае.
в) Если r = +¥, то для любой точки z ¹ 0 имеем 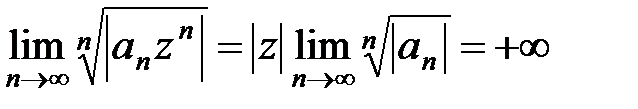 и поэтому ряд (10) при z ¹ 0 расходится. Это означает, что R = 0.
и поэтому ряд (10) при z ¹ 0 расходится. Это означает, что R = 0.
Таким образом, величина 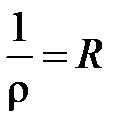 – радиус сходимости степенного ряда (10).
– радиус сходимости степенного ряда (10).
2) Теперь докажем формулу (15). Доказательство аналогично первому случаю. Обозначим 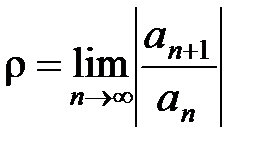 .
.
а) Пусть 0 < r < +¥ и пусть z 1– произвольная точка круга 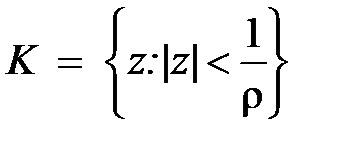 , тогда
, тогда 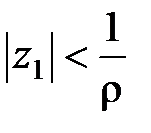 . Рассмотрим предел
. Рассмотрим предел
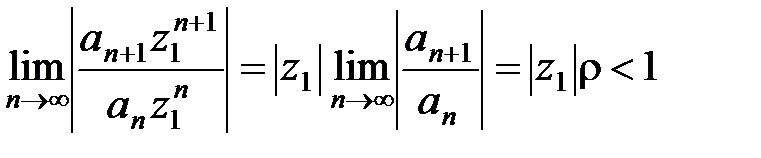 .
.
По признаку Даламбера (см. п.2.2) ряд 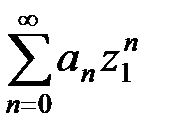 абсолютно сходится. Так как точка z 1– произвольная точка круга K, то ряд (10) абсолютно сходится в этом круге.
абсолютно сходится. Так как точка z 1– произвольная точка круга K, то ряд (10) абсолютно сходится в этом круге.
Пусть точка z 2лежит вне круга K, тогда 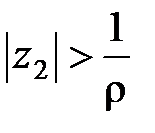 и поэтому
и поэтому
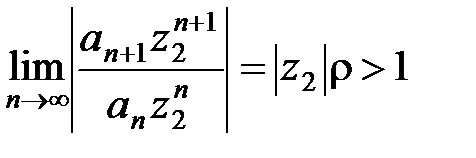 .
.
Следовательно, ряд 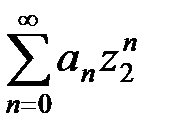 расходится при
расходится при 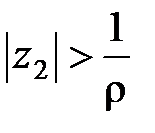 .
.
Если правая часть равенства (15) положительное число, то ряд (10) сходится в круге K и расходится вне этого круга. Значит, 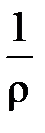 – радиус сходимости ряда (10).
– радиус сходимости ряда (10).
б) Если r= 0, то 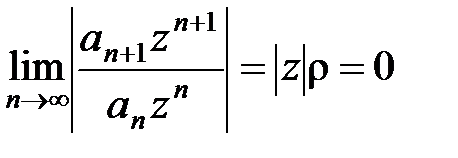 для любой точки z комплексной плоскости, и поэтому ряд (10) сходится при любом z. Это означает, что радиус сходимости ряда R = +¥ и формула (15) верна и в этом случае.
для любой точки z комплексной плоскости, и поэтому ряд (10) сходится при любом z. Это означает, что радиус сходимости ряда R = +¥ и формула (15) верна и в этом случае.
в) Если r = +¥, то для любой точки z ¹ 0 имеем 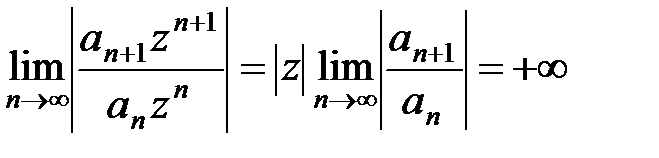 и поэтому ряд (10) при z ¹ 0 расходится. Это означает, что R = 0.
и поэтому ряд (10) при z ¹ 0 расходится. Это означает, что R = 0.
Таким образом, величина 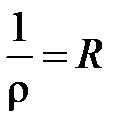 – радиус сходимости степенного ряда (10). ■
– радиус сходимости степенного ряда (10). ■
Если пределы 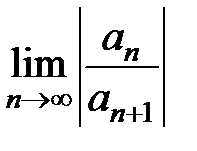 и
и 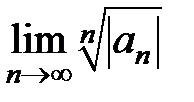 для степенного ряда
для степенного ряда 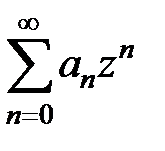 не существуют (как, например, для рядов только с четными или нечетными степенями z), то формулы (14) и (15) применять нельзя. Однако непосредственное использование признаков Даламбера и Коши для рядов
не существуют (как, например, для рядов только с четными или нечетными степенями z), то формулы (14) и (15) применять нельзя. Однако непосредственное использование признаков Даламбера и Коши для рядов 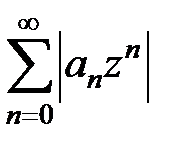 часто позволяет определить радиус круга сходимости.
часто позволяет определить радиус круга сходимости.
Все сказанное с помощью преобразования типа Z = z – z 0 (z – новая переменная, z 0 – фиксировано) переносится и на степенные ряды по степеням (z – z 0) вида (9). Областью сходимости такого ряда является круг вида | z – z 0| < R с точностью до его граничных точек. Этот круг называется кругом сходимости ряда (9), а R – его радиусом сходимости.
Областью сходимости степенного ряда с действительными членами
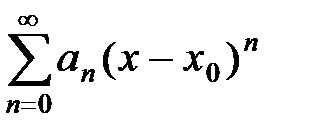
может оказаться либо интервал (x 0 – R, x 0 + R), либо отрезок [ x 0 – R, x 0 + R ], либо один из полуинтервалов (x 0 – R, x 0 + R ] или [ x 0 – R, x 0 + R). Если 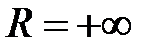 , то областью сходимости будет вся числовая ось, т.е. интервал
, то областью сходимости будет вся числовая ось, т.е. интервал 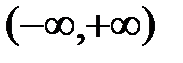 , если R = 0, то область сходимости будет состоять из одной точки x 0.
, если R = 0, то область сходимости будет состоять из одной точки x 0.
Для отыскания области сходимости степенного ряда
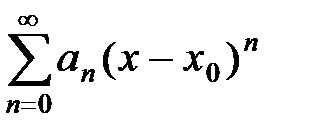
нужно сначала вычислить его радиус сходимости R (например, по одной из формул (14), (15)) и тем самым найти интервал сходимости (x 0 – R, x 0 + R), в котором ряд абсолютно сходится, затем исследовать сходимость ряда в концах интервала сходимости – в точках x = x 0 – R, x = x 0 + R.
Пример 6. Найти радиус сходимости и область сходимости ряда 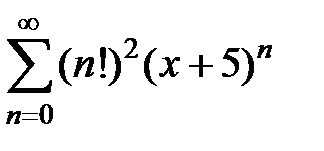 .
.
3Выпишем x 0= –5 и коэффициенты ряда an = (n!)2. Существует 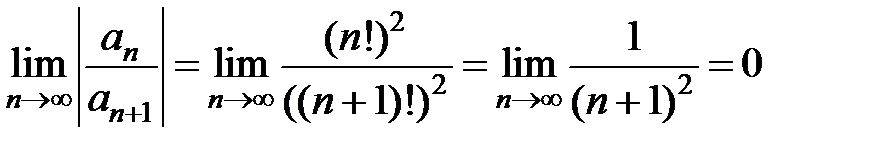 . Таким образом, радиус сходимости R = 0, область сходимость состоит из единственной точки x = –5.4
. Таким образом, радиус сходимости R = 0, область сходимость состоит из единственной точки x = –5.4
Пример 7. Найти радиус сходимости и область сходимости ряда 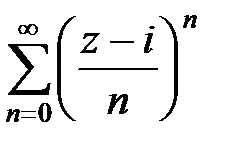 , z Î C.
, z Î C.
3Заметим, что z 0= i и 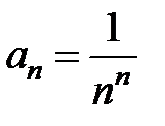 . Использую формулу (12), находим радиус сходимости ряда
. Использую формулу (12), находим радиус сходимости ряда 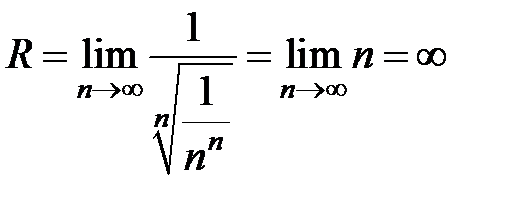 . Таким образом, R = ¥. Это означает, что ряд сходится всюду на комплексной плоскости C.4
. Таким образом, R = ¥. Это означает, что ряд сходится всюду на комплексной плоскости C.4
Пример 8. Найти радиус, интервал и область сходимости ряда 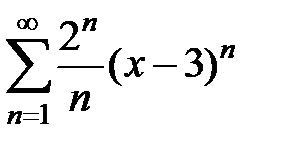 .
.
3Выпишем x 0= 3 и коэффициенты ряда 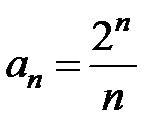 . Найдем
. Найдем 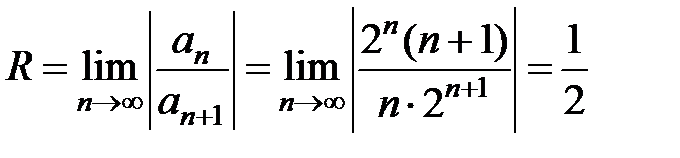 . Концы интервала сходимости
. Концы интервала сходимости 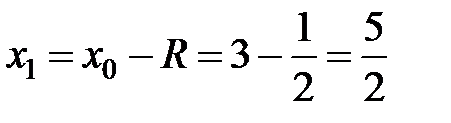 и
и 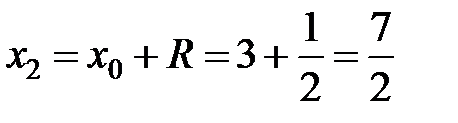 .
.
Итак, ряд абсолютно сходится для всех x из интервала 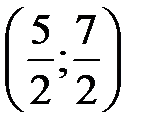 .
.
Исследуем поведение ряда на концах интервала сходимости. Подставляем в заданный ряд 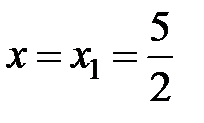 . Получится числовой ряд
. Получится числовой ряд 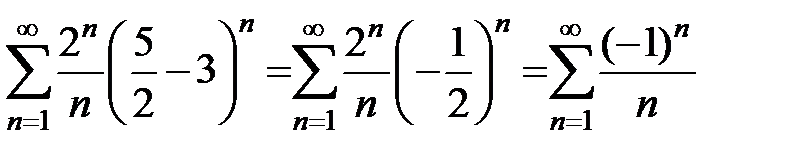 . Этот знакочередующийся ряд удовлетворяет условиям признака Лейбница, следовательно, он сходится.
. Этот знакочередующийся ряд удовлетворяет условиям признака Лейбница, следовательно, он сходится.
Подставим в заданный ряд 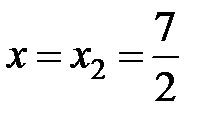 . Получим
. Получим 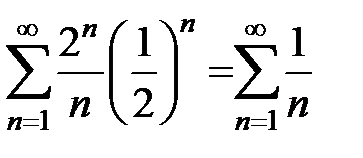 . Получили гармонический ряд, который, как известно, расходится.
. Получили гармонический ряд, который, как известно, расходится.
Итак, область сходимости – 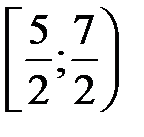 (к интервалу сходимости присоединился один из его концов).4
(к интервалу сходимости присоединился один из его концов).4
9.193. Сформулировать теорему Абеля для ряда (6).
9.194. Степенной ряд по степеням 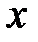 сходится в точке
сходится в точке 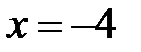 . Является ли этот ряд в точке
. Является ли этот ряд в точке 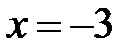 абсолютно сходящимся, условно сходящимся или расходящимся?
абсолютно сходящимся, условно сходящимся или расходящимся?
9.195. Пусть 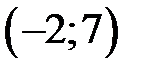 – интервал сходимости степенного ряда по степеням
– интервал сходимости степенного ряда по степеням 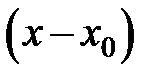 . Найти
. Найти 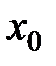 .
.
9.196. Пусть 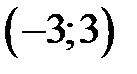 – интервал сходимости степенного ряда
– интервал сходимости степенного ряда 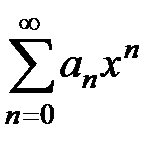 . Какой интервал сходимости имеет степенной ряд
. Какой интервал сходимости имеет степенной ряд 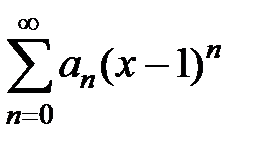 ?
?
9.197. Пусть 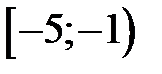 – область сходимости степенного ряда
– область сходимости степенного ряда 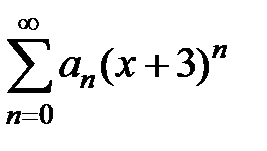 . Является ли ряд
. Является ли ряд 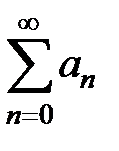 абсолютно сходящимся, условно сходящимся или расходящимся?
абсолютно сходящимся, условно сходящимся или расходящимся?
9.198. Радиусы сходимости двух степенных рядов по степеням 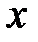 равны 5 и 6 (соответственно). Какой радиус сходимости имеет сумма этих рядов?
равны 5 и 6 (соответственно). Какой радиус сходимости имеет сумма этих рядов?
Найти радиус, интервал и область сходимости степенных рядов  .
.
9.199. 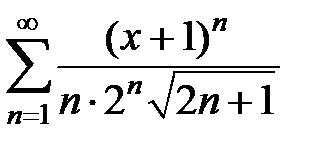 . .
| 9.200. 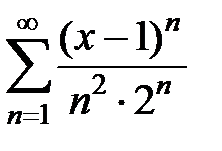 . .
|
9.201. 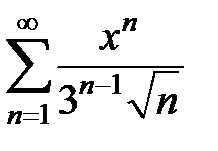 . .
| 9.202. 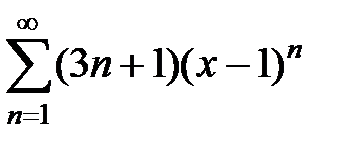 . .
|
9.203. 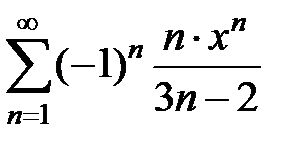 . .
| 9.204. 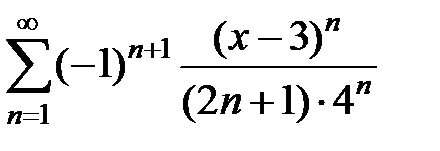 . .
|
9.205.  . .
| 9.206. 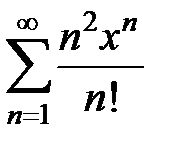 . .
|
9.207.  . .
| 9.208.  . .
|
Задачи повышенной сложности
Найти область сходимости степенных рядов 
209.  . .
| 210.  . .
|
211.  . .
| 212.  . .
|
213.  . .
| 214. 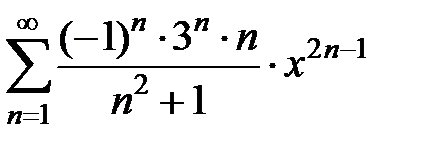 . .
|
215.  . .
| 216.  . .
|
217.  . .
| 218.  . .
|
Найти область абсолютной сходимости степенных рядов 
219.  . .
| 220.  . .
|
221.  . .
| 222.  . .
|
223.  . .
| 224.  . .
|
Найти суммы рядов
225.  . 226.
. 226.  .
.
5.3. Интегрирование и дифференцирование степенных рядов с действительными членами
Обратимся теперь к степенным рядам вида

|
|
|



 (1)
(1) сходится,то говорят, что функциональный ряд (1) сходится в точке x 0.
сходится,то говорят, что функциональный ряд (1) сходится в точке x 0. сходятся, то ряд (1) называется сходящимся на множестве D 1.
сходятся, то ряд (1) называется сходящимся на множестве D 1. называется абсолютно сходящимся на множестве D, если на множестве D сходится функциональный ряд
называется абсолютно сходящимся на множестве D, если на множестве D сходится функциональный ряд 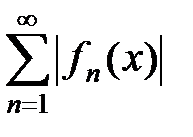 из модулей его членов.
из модулей его членов. называется суммой, а разность
называется суммой, а разность 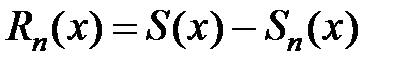 – остатком ряда.
– остатком ряда.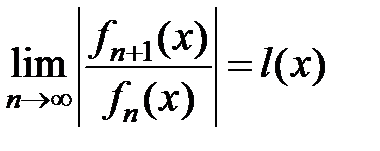 или
или  , то
, то , x Î R, x > -3.
, x Î R, x > -3. и x > -3, то, применяя признак Коши, имеем
и x > -3, то, применяя признак Коши, имеем 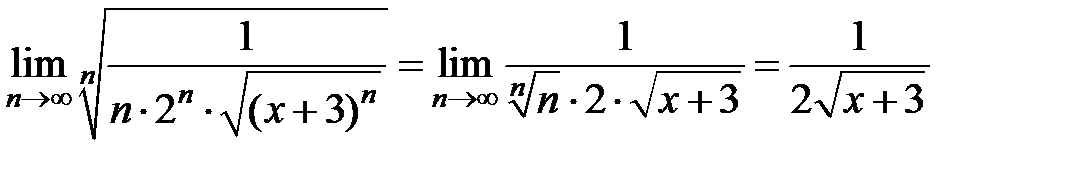 .
. , т.е. при
, т.е. при  . Ряд расходится, если
. Ряд расходится, если 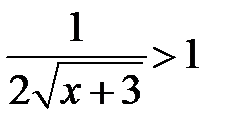 , т.е. при
, т.е. при  .
. получаем знакочередующийся ряд
получаем знакочередующийся ряд  , который сходится по признаку Лейбница. Таким образом, область сходимости ряда – полуинтервал
, который сходится по признаку Лейбница. Таким образом, область сходимости ряда – полуинтервал  .4
.4 .
. .
. , где n Î N, k Î Z, т.е. x ¹ 2 n –1p(2 k + 1).
, где n Î N, k Î Z, т.е. x ¹ 2 n –1p(2 k + 1).
 при 1 < x < 5.
при 1 < x < 5. , т.е. при x > 5 либо x < 1.
, т.е. при x > 5 либо x < 1. при x 1 = 1 и x 2 = 5.
при x 1 = 1 и x 2 = 5. .
. , то не выполняется необходимое условие сходимости числового ряда, значит, ряд
, то не выполняется необходимое условие сходимости числового ряда, значит, ряд  расходится. Аналогично доказывается расходимость ряда
расходится. Аналогично доказывается расходимость ряда  . Итак, области сходимости и абсолютной сходимости ряда совпадают с множеством D 1 Î (1;p) U (p;5).4
. Итак, области сходимости и абсолютной сходимости ряда совпадают с множеством D 1 Î (1;p) U (p;5).4 . Исследовать ряды на абсолютную сходимость.
. Исследовать ряды на абсолютную сходимость. .
.
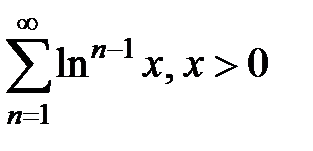 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
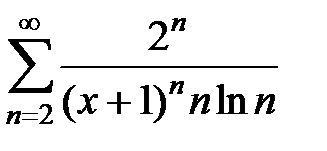 .
.
 .
.
 :
: .
.
 .
.
 .
.
 .
.

 называется равномерно сходящимся к функции f (x) в этой области, если для любого e > 0 найдется N = N (e) такое, что при всех n ≥ N (e) и x Î D 1
называется равномерно сходящимся к функции f (x) в этой области, если для любого e > 0 найдется N = N (e) такое, что при всех n ≥ N (e) и x Î D 1 .
.

 такой, что:
такой, что: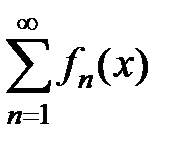 сходится абсолютно и равномерно в области D 1.
сходится абсолютно и равномерно в области D 1. , x Î R.
, x Î R. , так как
, так как  при x Î R.4
при x Î R.4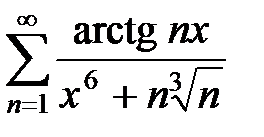 , x Î R.
, x Î R.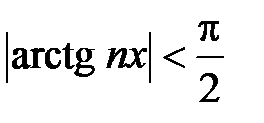 , то " x Î R и " n Î N имеем
, то " x Î R и " n Î N имеем  . Из сходимости мажорирующего ряда
. Из сходимости мажорирующего ряда  следует абсолютная и равномерная сходимость ряда
следует абсолютная и равномерная сходимость ряда 
 . Покажем, что в точке х = 0 сумма ряда имеет разрыв.
. Покажем, что в точке х = 0 сумма ряда имеет разрыв. .
.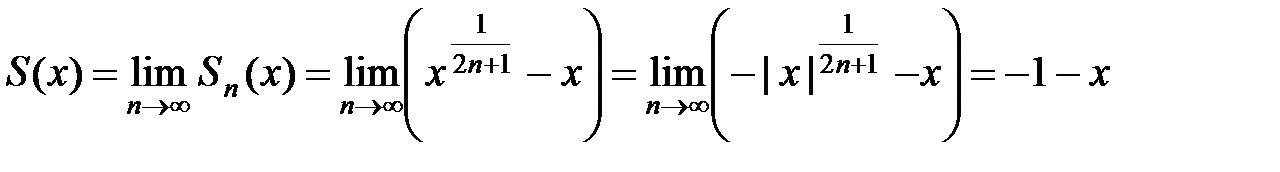 .
. .
. – мажорируемый, то при любом наперед заданном e > 0 найдется такой номер N, что при всех n ³ N, и в частности при n = N, будет выполняться неравенство
– мажорируемый, то при любом наперед заданном e > 0 найдется такой номер N, что при всех n ³ N, и в частности при n = N, будет выполняться неравенство ,
,
 (5)
(5) мажорируемый, то при любом x имеем | rn (x)| < e n, где e n ® 0 при n ® ¥. Поэтому
мажорируемый, то при любом x имеем | rn (x)| < e n, где e n ® 0 при n ® ¥. Поэтому .
. . Но из равенства (5) получаем:
. Но из равенства (5) получаем: .
. ,
,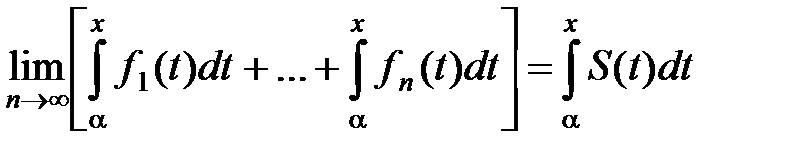 . (6)
. (6) (7)
(7) , т.е.
, т.е.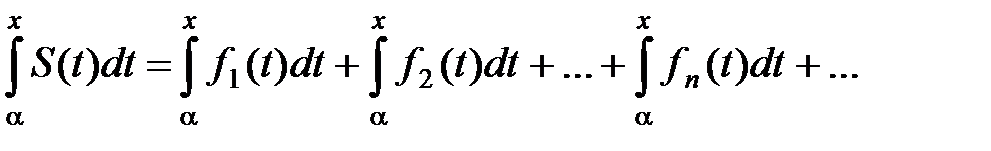 ,
, от суммы ряда
от суммы ряда  не всегда равен сумме интегралов от его членов (т.е. сумме ряда (7)).
не всегда равен сумме интегралов от его членов (т.е. сумме ряда (7)). , (8)
, (8) .
. ,
,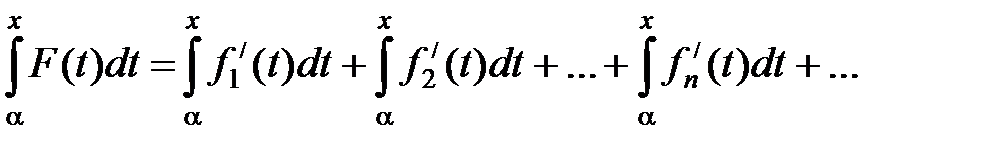

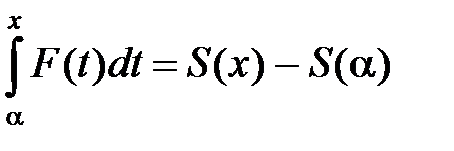 . Дифференцируя по х обе части последнего равенства, получим: F (x) = S /(x). ■
. Дифференцируя по х обе части последнего равенства, получим: F (x) = S /(x). ■ .
. .
. .
.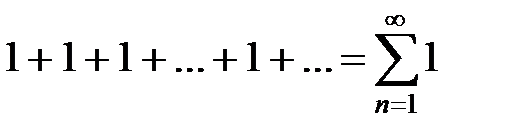 ,
, .
. .
.
 .
.
 .
.
 .
.
 .
.
 .
.
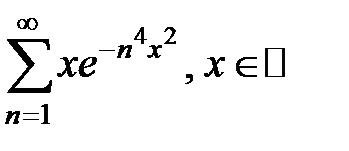 .
.
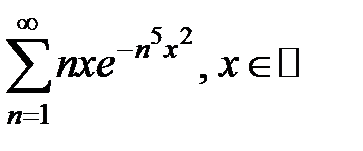 .
.
 функционального ряда
функционального ряда 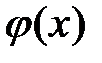 , то равномерная сходимость ряда не нарушится.
, то равномерная сходимость ряда не нарушится.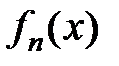 непрерывны в области
непрерывны в области 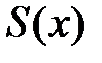 непрерывна в области
непрерывна в области 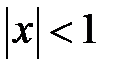 сумму и остаток ряда
сумму и остаток ряда 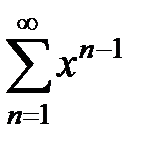 и показать, что он сходится равномерно на отрезке
и показать, что он сходится равномерно на отрезке 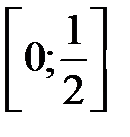 . При каком
. При каком 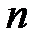 остаток
остаток 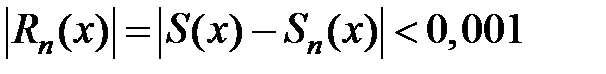 для любого
для любого 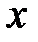 на этом отрезке?
на этом отрезке?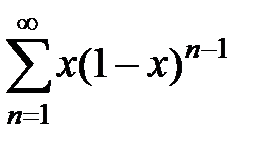 сходится неравномерно на отрезке
сходится неравномерно на отрезке 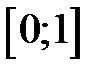 и равномерно на отрезке
и равномерно на отрезке 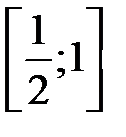 . При каком
. При каком 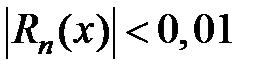 для любого
для любого 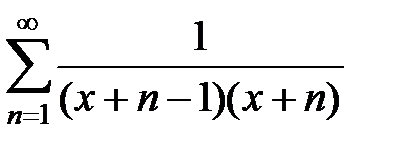 сходится равномерно к
сходится равномерно к 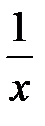 в интервале
в интервале 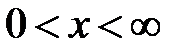 . При каком
. При каком 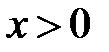 ) остаток ряда
) остаток ряда 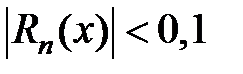 ?
?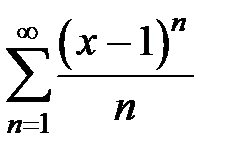 сходится равномерно на отрезке
сходится равномерно на отрезке 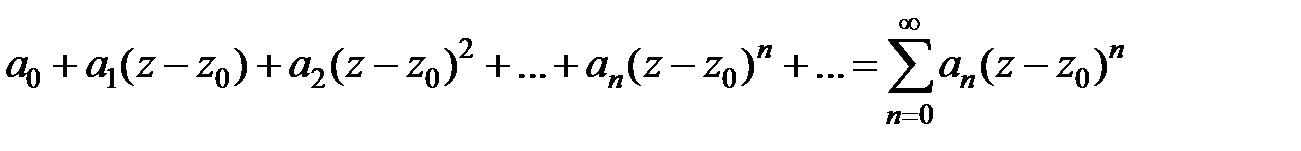 , (9)
, (9)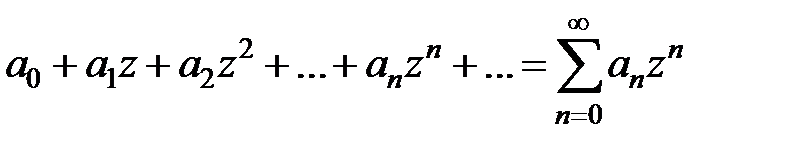 (10)
(10)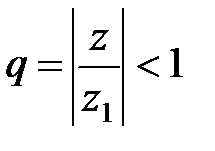 . (11)
. (11)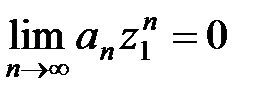 , откуда следует, что последовательность
, откуда следует, что последовательность 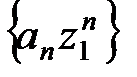 ограничена, т.е. существует число М > 0 такое, что
ограничена, т.е. существует число М > 0 такое, что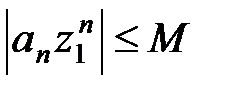 , n = 0, 1, 2,… (12)
, n = 0, 1, 2,… (12)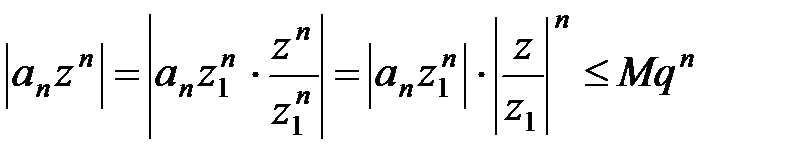 , где 0 £ q < 1. (13)
, где 0 £ q < 1. (13) , составленный из членов геометрической прогрессии со знаменателем 0 £ q < 1, сходится, то по признаку сравнения сходится и ряд
, составленный из членов геометрической прогрессии со знаменателем 0 £ q < 1, сходится, то по признаку сравнения сходится и ряд  , т.е. ряд (10) сходится абсолютно в каждой точке круга K 1.
, т.е. ряд (10) сходится абсолютно в каждой точке круга K 1.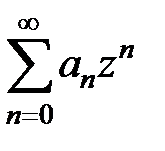 . Если R – неотрицательное число или +¥, обладает тем свойством, что при всех z, для которых | z | < R, этот ряд сходится, а при всех z, для которых | z | > R – расходится, то оно называется радиусом сходимости степенного ряда. Множество точек z, для которых | z | < R, называется – кругом сходимости ряда (в случае ряда с действительными членами интервал (– R, R) – интервалом сходимости).
. Если R – неотрицательное число или +¥, обладает тем свойством, что при всех z, для которых | z | < R, этот ряд сходится, а при всех z, для которых | z | > R – расходится, то оно называется радиусом сходимости степенного ряда. Множество точек z, для которых | z | < R, называется – кругом сходимости ряда (в случае ряда с действительными членами интервал (– R, R) – интервалом сходимости).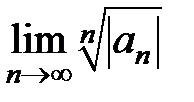 , то для радиуса R сходимости ряда (10) справедлива формула
, то для радиуса R сходимости ряда (10) справедлива формула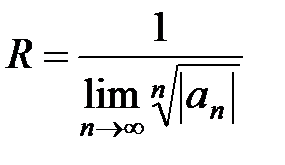 , (14)
, (14)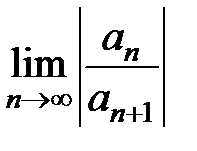 , то
, то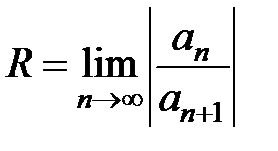 . (15)
. (15)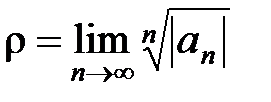 .
.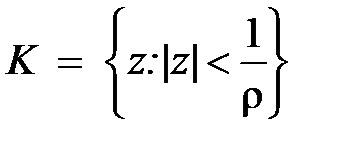 , тогда
, тогда 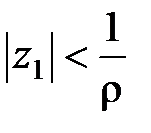 . Рассмотрим предел
. Рассмотрим предел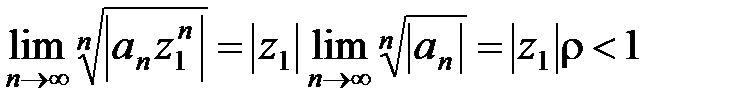 .
.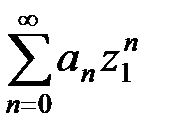 абсолютно сходится. Так как точка z 1– произвольная точка круга K, то ряд (10) абсолютно сходится в этом круге.
абсолютно сходится. Так как точка z 1– произвольная точка круга K, то ряд (10) абсолютно сходится в этом круге.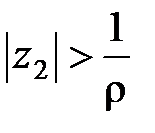 и поэтому
и поэтому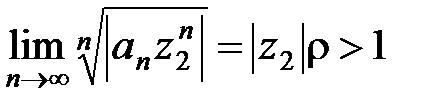 .
.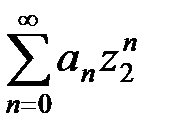 расходится при
расходится при 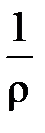 – радиус сходимости ряда (10).
– радиус сходимости ряда (10).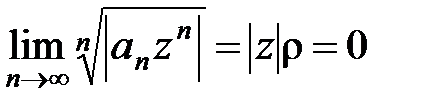 для любой точки z комплексной плоскости, и поэтому ряд (10) сходится при любом z. Это означает, что радиус сходимости ряда R = +¥ и формула (14) верна и в этом случае.
для любой точки z комплексной плоскости, и поэтому ряд (10) сходится при любом z. Это означает, что радиус сходимости ряда R = +¥ и формула (14) верна и в этом случае.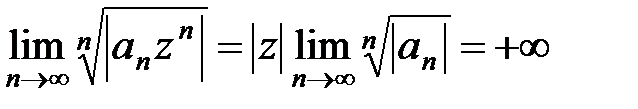 и поэтому ряд (10) при z ¹ 0 расходится. Это означает, что R = 0.
и поэтому ряд (10) при z ¹ 0 расходится. Это означает, что R = 0.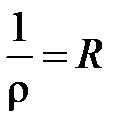 – радиус сходимости степенного ряда (10).
– радиус сходимости степенного ряда (10).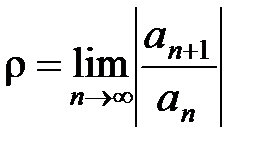 .
.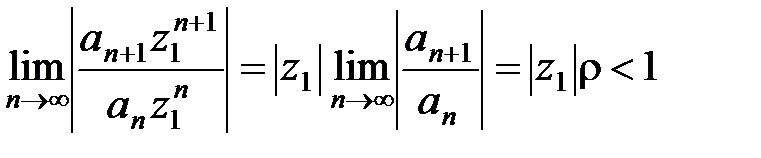 .
.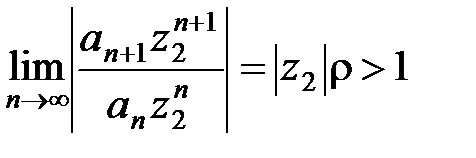 .
.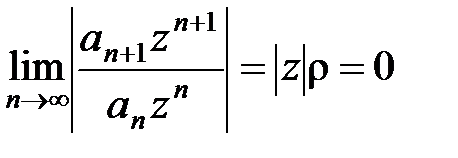 для любой точки z комплексной плоскости, и поэтому ряд (10) сходится при любом z. Это означает, что радиус сходимости ряда R = +¥ и формула (15) верна и в этом случае.
для любой точки z комплексной плоскости, и поэтому ряд (10) сходится при любом z. Это означает, что радиус сходимости ряда R = +¥ и формула (15) верна и в этом случае.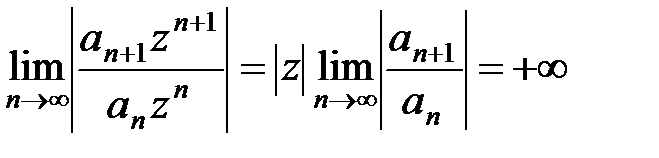 и поэтому ряд (10) при z ¹ 0 расходится. Это означает, что R = 0.
и поэтому ряд (10) при z ¹ 0 расходится. Это означает, что R = 0.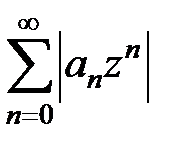 часто позволяет определить радиус круга сходимости.
часто позволяет определить радиус круга сходимости.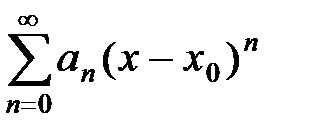
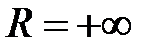 , то областью сходимости будет вся числовая ось, т.е. интервал
, то областью сходимости будет вся числовая ось, т.е. интервал 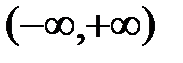 , если R = 0, то область сходимости будет состоять из одной точки x 0.
, если R = 0, то область сходимости будет состоять из одной точки x 0.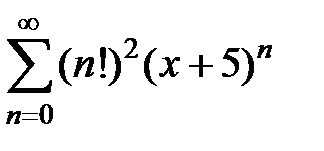 .
.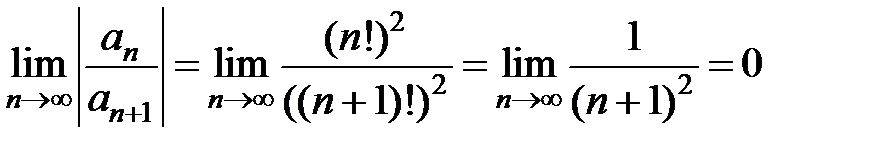 . Таким образом, радиус сходимости R = 0, область сходимость состоит из единственной точки x = –5.4
. Таким образом, радиус сходимости R = 0, область сходимость состоит из единственной точки x = –5.4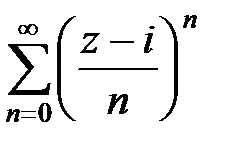 , z Î C.
, z Î C.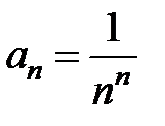 . Использую формулу (12), находим радиус сходимости ряда
. Использую формулу (12), находим радиус сходимости ряда 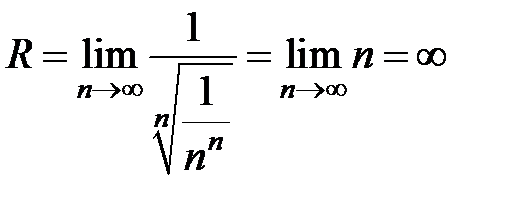 . Таким образом, R = ¥. Это означает, что ряд сходится всюду на комплексной плоскости C.4
. Таким образом, R = ¥. Это означает, что ряд сходится всюду на комплексной плоскости C.4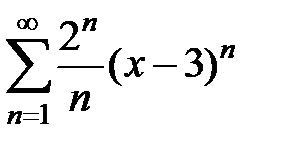 .
.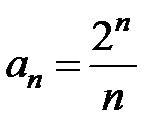 . Найдем
. Найдем 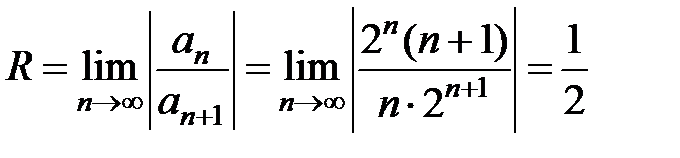 . Концы интервала сходимости
. Концы интервала сходимости 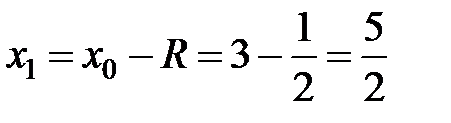 и
и 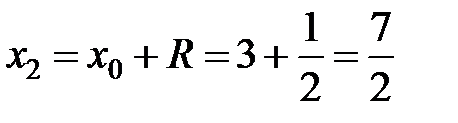 .
.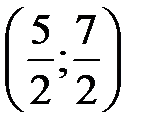 .
.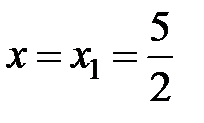 . Получится числовой ряд
. Получится числовой ряд 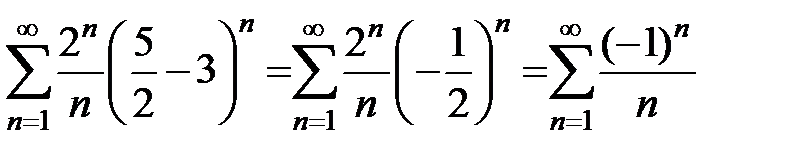 . Этот знакочередующийся ряд удовлетворяет условиям признака Лейбница, следовательно, он сходится.
. Этот знакочередующийся ряд удовлетворяет условиям признака Лейбница, следовательно, он сходится.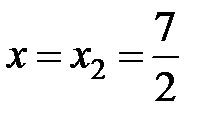 . Получим
. Получим 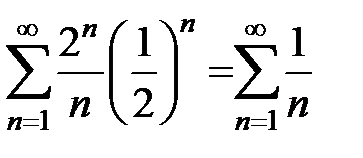 . Получили гармонический ряд, который, как известно, расходится.
. Получили гармонический ряд, который, как известно, расходится.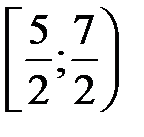 (к интервалу сходимости присоединился один из его концов).4
(к интервалу сходимости присоединился один из его концов).4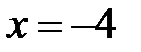 . Является ли этот ряд в точке
. Является ли этот ряд в точке 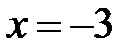 абсолютно сходящимся, условно сходящимся или расходящимся?
абсолютно сходящимся, условно сходящимся или расходящимся?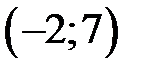 – интервал сходимости степенного ряда по степеням
– интервал сходимости степенного ряда по степеням 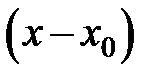 . Найти
. Найти 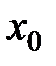 .
.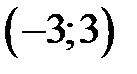 – интервал сходимости степенного ряда
– интервал сходимости степенного ряда 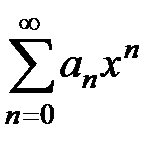 . Какой интервал сходимости имеет степенной ряд
. Какой интервал сходимости имеет степенной ряд 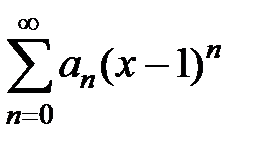 ?
?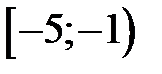 – область сходимости степенного ряда
– область сходимости степенного ряда 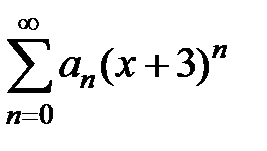 . Является ли ряд
. Является ли ряд 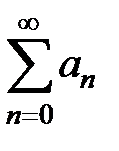 абсолютно сходящимся, условно сходящимся или расходящимся?
абсолютно сходящимся, условно сходящимся или расходящимся?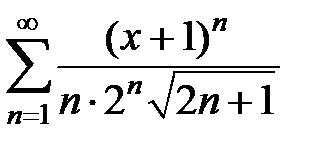 .
.
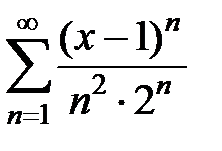 .
.
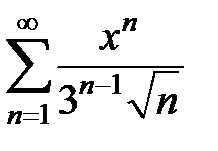 .
.
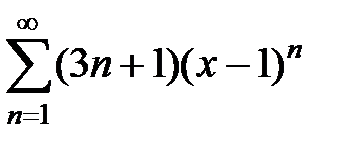 .
.
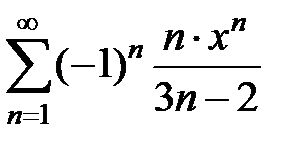 .
.
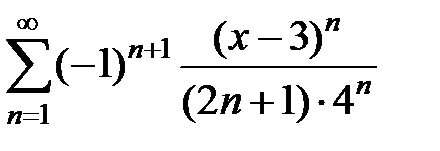 .
.
 .
.
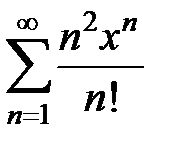 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
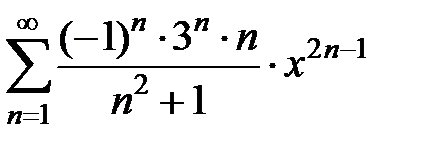 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 . 226.
. 226.  .
.


