Способы представления графов

Графы

1.1.1 Основные определения, представление графа в ЭВМ

1.1.1.1 Основные определения

Граф или неориентированный граф G — это упорядоченная пара G: = (V,E), для которой выполнены следующие условия:

V – это множество вершин или узлов,

E – это множество пар (в случае неориентированного графа — неупорядоченных) вершин, называемых рёбрами.

V (а значит и E) обычно считаются конечными множествами. Многие хорошие результаты, полученные для конечных графов, неверны (или каким-либо образом отличаются) для бесконечных графов. Это происходит потому, что ряд соображений становится ложным в случае бесконечных множеств.

Вершины и рёбра графа называются также элементами графа, число вершин в графе

|V| — порядком, число рёбер |E| — размером графа.

Вершины u и v называются концевыми вершинами (или просто концами) рёбра e = {u,v}. Ребро, в свою очередь, соединяет эти вершины. Две концевые вершины одного и того же ребра называются соседними.

Два ребра называются смежными, если они имеют общую концевую вершину.

Два ребра называются кратными, если множества их концевых вершин совпадают.

Ребро называется петлёй, если его концы совпадают, то есть e = {v,v}.

Степенью degV вершины V называют количество рёбер, для которых она является концевой (при этом петли считают дважды).

Вершина называется изолированной, если она не является концом ни для одного ребра; висячей (или листом), если она является концом ровно одного ребра.

Ориентированный граф (сокращённо орграф) G — это упорядоченная пара G: = (V,A), для которой выполнены следующие условия:

V – это множество вершин или узлов,

A – это множество (упорядоченных) пар различных вершин, называемых дугами или ориентированными рёбрами.

Дуга — это упорядоченная пара вершин (v, w), где вершину v называют началом, а w — концом дуги. Можно сказать, что дуга v w ведёт от вершины v к вершине w.

Смешанный граф G — это граф, в котором некоторые рёбра могут быть ориентированными, а некоторые — неориентированными. Записывается упорядоченной тройкой G: = (V,E,A), где V, E и A определены так же, как выше.

Понятно, что ориентированный и неориентированный графы являются частными случаями смешанного.

Обозначение связей: неориентированных - (A,B), ориентированных - <A,B>. Примеры изображений графов даны на рис.1. Скобочное представление графов, представленных на Рис. 3.1: а).((A,B),(B,A)) и б).(< A,B >,< B,A >).

Рис. 3.1. Граф неориентированный (а) и ориентированный (б).

Путём (или цепью) в графе называют конечную последовательность вершин, в которой каждая вершина (кроме последней) соединена со следующей в последовательности вершин ребром.

Ориентированным путём в орграфе называют конечную последовательность вершин v_i (i = 1, …, k), для которой все пары (v_i,v_i+1), (i = 1, …, k- 1), являются (ориентированными) рёбрами.

Циклом называют путь, в котором первая и последняя вершины совпадают. При этом длиной пути (или цикла) называют число составляющих его рёбер. Заметим, что если вершины u и v являются концами некоторого ребра, то согласно данному определению, последовательность (u,v,u) является циклом. Чтобы избежать таких «вырожденных» случаев, вводят следующие понятия.

Путь (или цикл) называют простым, если ребра в нём не повторяются; элементарным, если он простой и вершины в нём не повторяются. Несложно видеть, что:

· Всякий путь, соединяющий две вершины, содержит элементарный путь, соединяющий те же две вершины.

· Всякий простой неэлементарный путь содержит элементарный цикл.

· Всякий простой цикл, проходящий через некоторую вершину (или ребро), содержит элементарный (под-)цикл, проходящий через ту же вершину (или ребро).

Бинарное отношение на множестве вершин графа, заданное как «существует путь из u в v», является отношением эквивалентности, и, следовательно, разбивает это множество на классы эквивалентности, называемые компонентами связности графа. Если у графа ровно одна компонента связности, то граф связный. На компоненте связности можно ввести понятие расстояния между вершинами как минимальную длину пути, соединяющего эти вершины.

Всякий максимальный связный подграф графа G называется связной компонентой (или просто компонентой) графа G. Слово «максимальный» означает максимальный относительно включения, то есть не содержащийся в связном подграфе с большим числом элементов. Ребро графа называется мостом, если его удаление увеличивает число компонент.

Дополнительные характеристики графов

Граф называется:

· связным, если для любых вершин u,v есть путь из u в v.

· сильно связным или ориентированно связным, если он ориентированный, и из любой вершины в любую другую имеется ориентированный путь.

· деревом, если он связный и не содержит простых циклов.

· полным, если любые его две (различные, если не допускаются петли) вершины соединены ребром.

· двудольным, если его вершины можно разбить на два непересекающихся подмножества V₁ и V₂ так, что всякое ребро соединяет вершину из V₁ с вершиной из V₂.

· k-дольным, если его вершины можно разбить на k непересекающихся подмножества V₁, V₂, …, V_k так, что не будет рёбер, соединяющих вершины одного и того же подмножества.

· полным двудольным, если каждая вершина одного подмножества соединена ребром с каждой вершиной другого подмножества.

· планарным, если граф можно изобразить диаграммой на плоскости без пересечений рёбер.

· взвешенным, если каждому ребру графа поставлено в соответствие некоторое число, называемое весом ребра.

Алгоритмы на графах

Обход в глубину

При обходе в глубину посещается первый узел, а затем происходит перемещение вдоль ребер графа до тех пор, пока не встретится тупик. Узел неориентированного графа является тупиком, если все примыкающие к нему узлы уже были посещены. В орграфе тупиком также называется узел, из которого нет выходящих ребер. После попадания в тупик необходимо передвигаться назад вдоль пройденного пути до тех пор, пока не будет обнаружена вершина, у которой есть еще не посещенный сосед, и затем двигаться в этом новом направлении. Процесс оказывается завершенным, когда произошел возврат в отправную точку, и все примыкающие к ней вершины уже были посещены.

Рекурсивный алгоритм обхода в глубину приведен ниже:

DepthFirstTraversal(G,v)

G - граф

v - текущий узел

Visit(v)

Mark(v)

for каждого ребра vw графа G do

if вершина w непомечена then

DepthFirstTraversal(G,w)

end if

end for

Этот рекурсивный алгоритм использует системный стек для отслеживания текущей вершины графа, что позволяет правильно осуществить возвращение, наткнувшись на тупик. Можно построить нерекурсивный алгоритм, воспользовавшись стеком для сохранения и удаления информации о пройденных вершинах.

Обход по уровням

При обходе по уровням после посещения первого узла посещаются все соседние с ним вершины. При втором проходе посещаются все вершины, находящиеся на расстоянии двух ребер от начальной. При каждом новом проходе обходятся все вершины, расстояние от которых до начальной на единицу больше предыдущего. Для предупреждения повторного посещения необходимо либо вести список посещенных вершин, либо хранить информацию о посещении в соответствующей структуре данных узла. Ниже приведен пример реализации алгоритма обхода по уровням:

BreadthFirstTraversal(G,v)

G граф

v текущий узел

Visit(v)

Mark(v)

Enqueue(v)

while очередь непуста do

Dequeue(x)

for каждого ребра xw в графе G do

if вершина w непомечена then

Visit(w)

Mark(w)

Enqueue(w)

end if

end for

end while

Этот алгоритм заносит в очередь корень дерева обхода по уровням, но затем немедленно удаляет его из очереди. При просмотре соседних с корнем вершин он заносит их в очередь. После посещения всех соседних с корнем вершин происходит возвращение к очереди и обращение к первой вершине оттуда. Поскольку узлы добавляются к концу очереди, ни одна из вершин, находящихся на расстоянии двух ребер от корня, не будет рассмотрена повторно, пока не будут обработаны и удалены из очереди все вершины на расстоянии одного ребра от корня.

Алгоритм Дейкстры-Прима

Дейкстра и Прим предложили так называемый «жадный» алгоритм построения МОД. «Жадные» алгоритмы действуют, используя в каждый момент часть исходных данных и принимая лучшее решение на основе этой части. В рассматриваемом случае на каждом шаге имеется множество ребер, которые могут быть присоединены к уже построенной части остовного дерева, из них выбирается ребро с наименьшим весом. Вершины графа разбиваются на три класса: вершины, вошедшие в уже построенную часть дерева, вершины, окаймляющие построенную часть, и еще не рассмотренные вершины. Алгоритм начинает работу с произвольной вершины графа, которая включается в остовное дерево. Все вершины, соединенные (соседние) с данной, заносятся в кайму. Затем выполняется цикл поиска ребра с наименьшим весом, соединяющего уже построенную часть остовного дерева с каймой; это ребро вместе с новой вершиной добавляется в дерево и происходит обновление каймы таким образом, чтобы список ребер из дерева в кайму включал ребра с наименьшими весами. После того, как в дерево попадут все вершины, работа будет закончена. Словесный алгоритм приведен ниже:

Шаг 1. Выбрать начальный узел

Шаг 2. Сформировать начальную кайму, состоящую из вершин, соседних с начальным узлом

Шаг 3. В графе есть вершины, не попавшие в дерево?

Если да, то переход на Шаг 4.

Иначе – переход на Шаг 9.

Шаг 4. Выбрать ребро из дерева в кайму с наименьшим весом

Шаг 5. Добавить конец ребра к дереву

Шаг 6. Изменить кайму, для чего добавить в кайму вершины, соседние с новой

Шаг 7. Обновить список ребер из дерева в кайму так, чтобы он состоял из ребер наименьшего веса

Шаг 8. Переход на Шаг 3

Шаг 9. Конец

На Рис. 3.6 изображен исходный граф:

Рис. 3.6. Исходный граф

Рис. 3.7. Добавление первой вершины. Пунктиры ведут к вершинам каймы

Рис. 3.8. Добавление второй и третьей вершин

Рис. 3.9. Добавление четвертой и пятой вершин

Рис. 3.10. Заключительные шаги алгоритма Дейкстры-Прима

Алгоритм Крускала

Другой алгоритм построения МОД предложил Крускал. Алгоритм начинает работу с пустого дерева. К нему добавляются ребра в порядке возрастания их весов до тех пор, пока не будет получен набор ребер, объединяющий все вершины графа. В процессе выполнения необходимо не допускать добавление ребер, приводящих к появлению цикла в создаваемом дереве. Если ребра закончатся до того, как все вершины будут соединены между собой, это означает, что граф был несвязным, и полученный результат представляет собой объединение МОД всех его компонент связности. Пример алгоритма приведен ниже:

1. Отсортировать ребра в порядке возрастания весов

2. Инициализировать структуру разбиений

edgeCount=l

while edgeCount<=E and includedCount<=N-l do

parentl=FindRoot(edge[edgeCount].start)

parent2=FindRoot(edge[edgeCount].end)

if parentl/=parent2 then

добавить edge[edgeCount] в остовное дерево

includedCount=includedCount+l

Union(parent1,parent2)

end if

edgeCount=edgeCount+l

end while

 

Для иллюстрации действия алгоритма будем использовать граф, приведенный на Рис. 3.6.

Рис. 3.11. Добавление первого ребра

Рис. 3.12. Добавление второго и третьего ребра

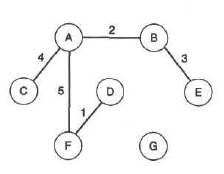
Рис. 3.13. Добавление четвертого и пятого ребер

Рис. 3.14. Заключительные шаги алгоритма Крускала

Алгоритм Дейкстры

Результатом алгоритма поиска кратчайшего пути является последовательность ребер, соединяющая заданные две вершины и имеющая наименьшую длину среди всех таких последовательностей.

Жадный алгоритм построения минимального остовного дерева непригоден для поиска кратчайшего пути между двумя вершинами, поскольку на каждом проходе он учитывает длину лишь одного ребра.

Если же изменить его так, чтобы при выборе ребра, ведущего в кайму, он выбирал ребро, являющееся частью кратчайшего в целом пути из начальной вершины, то мы получим требуемый результат. Точнее говоря, вот измененный алгоритм:

Шаг 1. Выбрать начальную вершину

Шаг 2. Создать начальную кайму из вершин, соединенных с начальной

Шаг 3. Вершина назначения не достигнута?

Если нет, то переход на Шаг 4.

Иначе – переход на Шаг 9

Шаг 4. Выбрать вершину каймы с кратчайшим расстоянием до начальной

Шаг 5. Добавить эту вершину и ведущее в нее ребро к дереву

Шаг 6. Изменить кайму путем добавления к ней вершин, соединенных с вновь добавленной

Шаг 7. Для всякой вершины каймы выполнить: приписать к ней ребро, соединяющее ее с деревом и завершающее кратчайший путь к начальной вершине

Шаг 8. Переход на Шаг 3

Шаг 9. Конец

Проиллюстрируем алгоритм на примере графа, приведенного на Рис. 3.6. Будем искать кратчайший путь от вершины A к вершине G.

Рис. 3.15. Начальная вершина

 

 

Рис. 3.16. Добавление второй и третьей вершин

Рис. 3.17. Добавление четвертой и пятой вершин

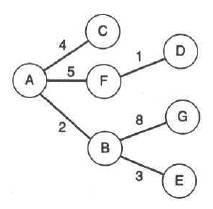
Рис. 3.18. Заключительные шаги алгоритма Дейкстры

 

Графы

1.1.1 Основные определения, представление графа в ЭВМ

1.1.1.1 Основные определения

Граф или неориентированный граф G — это упорядоченная пара G: = (V,E), для которой выполнены следующие условия:

V – это множество вершин или узлов,

E – это множество пар (в случае неориентированного графа — неупорядоченных) вершин, называемых рёбрами.

V (а значит и E) обычно считаются конечными множествами. Многие хорошие результаты, полученные для конечных графов, неверны (или каким-либо образом отличаются) для бесконечных графов. Это происходит потому, что ряд соображений становится ложным в случае бесконечных множеств.

Вершины и рёбра графа называются также элементами графа, число вершин в графе

|V| — порядком, число рёбер |E| — размером графа.

Вершины u и v называются концевыми вершинами (или просто концами) рёбра e = {u,v}. Ребро, в свою очередь, соединяет эти вершины. Две концевые вершины одного и того же ребра называются соседними.

Два ребра называются смежными, если они имеют общую концевую вершину.

Два ребра называются кратными, если множества их концевых вершин совпадают.

Ребро называется петлёй, если его концы совпадают, то есть e = {v,v}.

Степенью degV вершины V называют количество рёбер, для которых она является концевой (при этом петли считают дважды).

Вершина называется изолированной, если она не является концом ни для одного ребра; висячей (или листом), если она является концом ровно одного ребра.

Ориентированный граф (сокращённо орграф) G — это упорядоченная пара G: = (V,A), для которой выполнены следующие условия:

V – это множество вершин или узлов,

A – это множество (упорядоченных) пар различных вершин, называемых дугами или ориентированными рёбрами.

Дуга — это упорядоченная пара вершин (v, w), где вершину v называют началом, а w — концом дуги. Можно сказать, что дуга v w ведёт от вершины v к вершине w.

Смешанный граф G — это граф, в котором некоторые рёбра могут быть ориентированными, а некоторые — неориентированными. Записывается упорядоченной тройкой G: = (V,E,A), где V, E и A определены так же, как выше.

Понятно, что ориентированный и неориентированный графы являются частными случаями смешанного.

Обозначение связей: неориентированных - (A,B), ориентированных - <A,B>. Примеры изображений графов даны на рис.1. Скобочное представление графов, представленных на Рис. 3.1: а).((A,B),(B,A)) и б).(< A,B >,< B,A >).

Рис. 3.1. Граф неориентированный (а) и ориентированный (б).

Путём (или цепью) в графе называют конечную последовательность вершин, в которой каждая вершина (кроме последней) соединена со следующей в последовательности вершин ребром.

Ориентированным путём в орграфе называют конечную последовательность вершин v_i (i = 1, …, k), для которой все пары (v_i,v_i+1), (i = 1, …, k- 1), являются (ориентированными) рёбрами.

Циклом называют путь, в котором первая и последняя вершины совпадают. При этом длиной пути (или цикла) называют число составляющих его рёбер. Заметим, что если вершины u и v являются концами некоторого ребра, то согласно данному определению, последовательность (u,v,u) является циклом. Чтобы избежать таких «вырожденных» случаев, вводят следующие понятия.

Путь (или цикл) называют простым, если ребра в нём не повторяются; элементарным, если он простой и вершины в нём не повторяются. Несложно видеть, что:

· Всякий путь, соединяющий две вершины, содержит элементарный путь, соединяющий те же две вершины.

· Всякий простой неэлементарный путь содержит элементарный цикл.

· Всякий простой цикл, проходящий через некоторую вершину (или ребро), содержит элементарный (под-)цикл, проходящий через ту же вершину (или ребро).

Бинарное отношение на множестве вершин графа, заданное как «существует путь из u в v», является отношением эквивалентности, и, следовательно, разбивает это множество на классы эквивалентности, называемые компонентами связности графа. Если у графа ровно одна компонента связности, то граф связный. На компоненте связности можно ввести понятие расстояния между вершинами как минимальную длину пути, соединяющего эти вершины.

Всякий максимальный связный подграф графа G называется связной компонентой (или просто компонентой) графа G. Слово «максимальный» означает максимальный относительно включения, то есть не содержащийся в связном подграфе с большим числом элементов. Ребро графа называется мостом, если его удаление увеличивает число компонент.

Дополнительные характеристики графов

Граф называется:

· связным, если для любых вершин u,v есть путь из u в v.

· сильно связным или ориентированно связным, если он ориентированный, и из любой вершины в любую другую имеется ориентированный путь.

· деревом, если он связный и не содержит простых циклов.

· полным, если любые его две (различные, если не допускаются петли) вершины соединены ребром.

· двудольным, если его вершины можно разбить на два непересекающихся подмножества V₁ и V₂ так, что всякое ребро соединяет вершину из V₁ с вершиной из V₂.

· k-дольным, если его вершины можно разбить на k непересекающихся подмножества V₁, V₂, …, V_k так, что не будет рёбер, соединяющих вершины одного и того же подмножества.

· полным двудольным, если каждая вершина одного подмножества соединена ребром с каждой вершиной другого подмножества.

· планарным, если граф можно изобразить диаграммой на плоскости без пересечений рёбер.

· взвешенным, если каждому ребру графа поставлено в соответствие некоторое число, называемое весом ребра.

Способы представления графов