Понятие экономико-математической модели производственной системы. Задача и методы.
Экономико-математические методы и модели (ЭММиМ) предназначены для поиска и обоснования путей повышения эффективности производства, рационального использования ресурсов, обеспечения конкурентоспособности предприятий в условиях рыночной экономики. На основе ЭММиМ с помощью современных компьютерных технологий получают данные для анализа эффективности производственных систем, прогнозирования их поведения при возможных изменениях производственной ситуации и выработки управленческих решений для достижения поставленных целей.
 Экономико-математической модель – это формализованное (математическое) описание условий и результатов функционирования производственной системы с позиций экономики. Модель строится с помощью переменных, параметров, множеств, функций, уравнений, неравенств, логических правил.
Экономико-математической модель – это формализованное (математическое) описание условий и результатов функционирования производственной системы с позиций экономики. Модель строится с помощью переменных, параметров, множеств, функций, уравнений, неравенств, логических правил.
 Найти max (min)
Найти max (min)
при условиях


 где f, gi , - заданные, в общем случае нелинейные функции n переменных -
где f, gi , - заданные, в общем случае нелинейные функции n переменных -
bi – заданные параметры.
 Запись означает, что может иметь место неравенство вида, уравнение или неравенство вида.
Запись означает, что может иметь место неравенство вида, уравнение или неравенство вида.
В экономических приложениях функцию f называют целевой функцией.
Если f и gi , - линейные функции, то имеет место задача линейного программирования.
Двойственность в линейном программировании.
Число неизвестных двойственной задачи равно числу основных ограничений исходной задачи и, наоборот.
Матрица основных ограничений двойственной задачи образуется путем транспонирования соответствующей матрицы исходной задачи.
Параметрами ограничений (правыми частями) двойственной задачи служат коэффициенты при неизвестных в целевой функции исходной задачи и, наоборот.

 Знаки неравенств основных ограничений двойственной задачи противоположны знакам неравенств основных ограничений исходной задачи; если исходная задача - на максимум, то двойственная к ней - на минимум и, наоборот.
Знаки неравенств основных ограничений двойственной задачи противоположны знакам неравенств основных ограничений исходной задачи; если исходная задача - на максимум, то двойственная к ней - на минимум и, наоборот.

 Найти min z = max f =
Найти min z = max f =
при условиях
yi, i=1,...,m - неизвестные двойственной задачи (условные цены ресурсов).
Условные цены ресурсов отражают значимость ресурсов в конкретных условиях данной производственной ситуации
Теоремы двойственности.
 Теоремы двойственности устанавливают взаимосвязь между оптимальными решениями прямой и двойственной задач.
Теоремы двойственности устанавливают взаимосвязь между оптимальными решениями прямой и двойственной задач.
Согласно первой теореме двойственности суммарная стоимость ресурсов по оптимальным условным ценам равна общей прибыли от реализации всей продукции, изготовленной предприятием при оптимальном плане выпуска продукции из имеющихся запасов ресурсов.
Содержание и порядок проведения постоптимизационного оптимального решения задач.
Разработка рекомендаций по заблаговременной организационно-технологической подготовке производства на случай возможных изменений производственной ситуации.
Разработка субоптимального плана, не слишком сильно отличающегося от теоретически оптимального по суммарной прибыли, но более удобного с точки зрения организации производства.
Для ее решения применяется интерактивный метод ветвей и границ: решение исходной задачи нелинейного целочислен-ного программирования сводится к решению последователь-ности порожденных задач линейного целочисленного программирования, каждая из которых формируется в интерактивном режиме с учетом ограничений, связанных с пороговыми значениями объемов выпуска продукции.
а) Решение целочисленной задачи планирования производства с пороговыми значениями объемов выпуска продукции начинается с определения текущего плана для базовой системы ограничений, включающей условие целочисленности значений неизвестных, но не учитывающей пороговые значения объемов выпуска продукции.
Если получен приемлемый допустимый план, то задача решена. Если получен допустимый план, не являющийся приемлемым, то задача решения не имеет. Наконец, если текущий план для исходной задачи оказался приемлемым, но недопустимым, то реализуется алгоритм целенаправленного перебора текущих планов, связанный с формированием в интерактивном режиме множества порожденных задач и их последовательным решением с помощью пакета “Поиск решения”.
б) Если на некотором шаге в результате решения одной из порожденных задач получен неприемлемый текущий план, то убивается соответствующая ему ветвь иерархической структуры порожденных задач.
Если получен приемлемый, но недопустимый план, в котором положительная компонента pj меньше порогового значения dj, то производится дробление очередной задачи на две порожденные задачи: для первой из пары порожденных задач в систему ограничений вводится дополнительное условие pj = 0 и условие pj ³ dj для второй порожденной задачи.
При условиях

Найти min f =
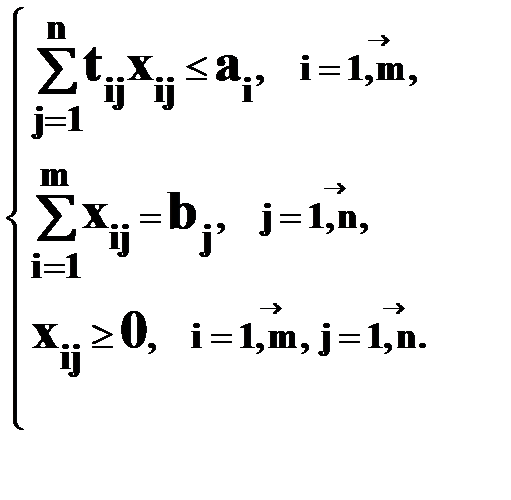 при условиях
при условиях
pij равно 1, если j-й заказ распределяется на i-ю машину,
и 0 в противном случае.
Каждая партия проходит обработку на одной из машин участка, т.е. используется определенный технологический маршрут для каждой партии изделий. Для каждого заказа (вида продукции) может быть выделено несколько допустимых маршрутов, поэтому возникает задача выбора оптимальных технологических маршрутов и интенсивности их загрузки (оптимальных объемов партий), обеспечивающих минимальные суммарные затраты на выполнение всех заказов в установленных объемах.
nm – общее число технологических маршрутов;
m – индекс маршрута (m = 1, …, nm);
Mj, j = 1, …, n – множество индексов маршрутов, связанных с обработкой j-го заказа;
Mki, k = 1, …, q; i = 1, …, mk – множество индексов маршрутов, связанных с использованием i-й машины k-го участка;
xm, m = 1, …, nm – количество учетных единиц заказа, обрабатываемых с использованием m-го технологического маршрута;
tkim, k = 1, …, q; i = 1, …, mk; m = 1, …, nm – затраты машинного времени
i-й машины k-го участка, при обработке одной учетной единицы продукции на m-м технологическом маршруте;
sm, m = 1, …, nm – затраты на обработку одной учетной единицы продукции на m-м технологическом маршруте;
zkm, k = 1, …, q; m = 1, …, nm – затраты на обработку одной учетной единицы продукции на k-м участке для m-го технологического маршрута
 Найти min f =
Найти min f =
 при условиях
при условиях

где:
Пример задачи оптимизации технологических маршрутов
Рассчитать оптимальный план загрузки производственного оборудования формного цеха. Цех должен изготовить стереотипы текстовых форм по двум заказам. По первому заказу производственная программа составляет 20 стереотипов (листов набора), по второму – 30 стереотипов. Процесс изготовления стереотипов включает три последовательно выполняемые технологические операции (на трех участках). Первая операция (набор) может выполняться на трех видах взаимозаменяемого оборудования, вторая операция (изготовление оригиналов форм) – на двух видах взаимозаменяемого оборудования, третья операция (получение стереотипов) – на двух видах оборудования.
При условиях

xij – число единиц груза, подлежащих перевозке из i -го пункта отправления в j -й пункт назначения;
Задача о назначениях.
Частным случаем транспортной задачи является следующая задача о назначениях. Имеется n должностей и
n претендентов на эти должности. Известна полезность каждого претендента при назначении на каждую из должностей, т.е. задана матрица cij, i,j=1,...,n. Требуется произвести назначение каждого претендента на одну из должностей, обеспечив при этом максимальную суммарную полезность назначений.
Обозначим через xij, i,j=1,...,n неизвестные, которые будут принимать значение, равное единице, если i-й претендент получает назначение на j-ю должность, и нулю - в противном случае; через f обозначим суммарную полезность назначений.
 Найти max f =
Найти max f =
 при условиях
при условиях
Переменные, которые могут принимать одно из двух значений: 0 или 1, называются булевыми (двоичными) переменными. Задача о назначениях является задачей с булевыми неизвестными - частным случаем задачи целочисленного линейного программирования.
Примеры задач нелинейного программирования
К числу задач нелинейного программирования относятся:
• задача оптимизации последовательности обработки заказов (решается методом случайного поиска),
• задача оптимизации сроков замены оборудования (решается методом динамического программирования),
• задача управления запасами (для ее решения применяется классический аппарат поиска экстремума функции нескольких переменных).
На этапе постоптимизационного анализа задач линейного и нелинейного программирования используются методы целочисленного и параметрического программирования. При решении задач в стохастической постановке применяется метод компьютерного моделирования и используются эконометрические модели для обработки результатов моделирования.
Ключевым вопросом долгосрочного планирования является выработка оптимальной политики обновления производственных мощностей предприятия. Особенно актуальна эта задача для полиграфических предприятий в связи с высоким возрастом печатных машин.
Научно-технический прогресс в отрасли приводит к моральному старению эксплуатирующейся машины, которое проявляется в том, что ежегодно появляются новые модели (поколения) машины с лучшими технико-экономическими показателями.
Явление физического и морального старения машины учитывается в модели с помощью семейств кривых S(p,t) и C(p,t). Первое из них характеризует зависимость годовой прибыли от возраста и поколения машины, второе – затраты на замену машины.
Затратив необходимую сумму средств, приобрести новую машину с тем, чтобы в текущем году и в последующие годы получать более высокую прибыль, что позволит через некоторое время компенсировать затраты на обновление машины и, возможно, накопить к концу рассматриваемого периода суммарную прибыль в большем объеме, чем при эксплуатации старой машины.
 Оптимальная политика замены машины формируется из условия максимизации суммарной прибыли за весь планируемый период N с учетом затрат на замену машины (инвестиций) и определяется с помощью функциональных уравнений P.Беллмана
Оптимальная политика замены машины формируется из условия максимизации суммарной прибыли за весь планируемый период N с учетом затрат на замену машины (инвестиций) и определяется с помощью функциональных уравнений P.Беллмана
fn (t) = max
n = N-1, N-2,..., 1; t = 1, 2,...,
где fn(t) - максимальная прибыль при оптимальной политике замены за n-й и
• последующие годы планового периода при возрасте машины t лет к началу n-го года (следовательно, речь идет о машине (n - t)-го поколения);
Sn(t) - годовая прибыль в n-м году для машины возраста t лет;
Cn(t) - затраты в n-м году на замену машины возраста t лет;
a- коэффициент дисконтирования, учитывающий уровень изменения цен.
 Функция f полагается равной нулю для значений n ³ N+1, следовательно,
Функция f полагается равной нулю для значений n ³ N+1, следовательно,
fN (t) = max
t = 1, 2,...,
Вычислив значения fN(t), t=1,2,... и используя приведенные выше функциональные уравнения, можно найти последовательно значения
fN-1(t), fN-2(t),..., f1(t), t=1, 2,... при оптимальной политике замены оборудования. Значение f1(t) соответствует суммарной прибыли от процесса эксплуатации машины, начавшегося в первый год планового периода при возрасте машины t лет, при соблюдении оптимальной стратегии замены машины. Информация, полученная в результате решения рассматриваемой задачи, позволяет разложить суммарную прибыль f1(t) по годам планового периода и определить, сколько раз и в какие годы планового периода следует произвести замену машины, чтобы добиться наилучшего эффекта.
“Обратный” ход в решении задачи о замене оборудования
Значение в ячейке AG80, равное 10,24 расчетных д.ед., является результатом так называемого “прямого” хода в решении рассматриваемой задачи. Оно характеризует величину суммарной прибыли за весь плановый период при оптимальной политике замены машины. Чтобы найти оптимальные сроки замены машины, а также разложить суммарную прибыль по годам планового периода и определить необходимые затраты (инвестиции), связанные с заменой (или заменами) машины, необходимо выполнить “обратный” ход.
При выполнении обратного хода используется информация для каждого года планового периода и каждого возраста машины об оптимальном выборе одного из альтернативных решений: продолжить эксплуатацию действующей машины или произвести ее замену. Эта информация формируется в виде треугольной матрицы инвестиций. Если в текущем году планового периода при данном возрасте машины оптимальным решением является продолжение эксплуатации действу-ющей машины, то в соответствующую ячейку матрицы инвестиций заносится ноль, иначе – стоимость замены действующей машины.
Объем необходимых инвестиций в ряде случаев может быть сдерживающим фактором для практической реализации теоретически оптимальной стратегии замены оборудования. В этой связи актуальной является двухкритериальная задача о замене оборудования с использованием суммарной прибыли в качестве одного критерия, величина которого максимизируется, и объема инвестиций в качестве второго критерия, который минимизируется при выборе оптимальной политики замены оборудования.
Решение рассматриваемой задачи двухкритериальной оптимизации связано с анализом множества допустимых политик замены оборудования (альтернатив), на котором вводится отношение доминирования по Парето. Определим его следующим образом: политика Ai доминирует по Парето политику Aj, если хотя бы по одному из двух выбранных критериев (целевых функций) превосходит политику Aj и не уступает ей по другому критерию.
Политика Ak является недоминируемой, если на множестве допустимых политик нет ни одной политики, по отношению к которой она была бы доминируемой. Подмножество недоминируемых политик образует общее (базовое) решение рассматриваемой двухкритериаль-ной задачи.
Решение двухкритериальной задачи о замене оборудования проводится в три этапа. На первом этапе формируется множество допустимых политик, перспективных с точки зрения их возможного использования в качестве оптимального решения двухкритериаль-ной задачи. Как правило, практический интерес представляют допустимые политики с числом замен машины, не превышающем трех.
Для формирования множества допустимых политик необходимо решать задачу о замене оборудования в обратной постановке: по заданным априори срокам замены машины находить соответствующие им значения суммарной прибыли и объема необходимых инвестиций.
На втором этапе выделяется подмножество недоминируемых политик, которое является общим решением двухкритериальной задачи. На заключительном, третьем этапе методом уступок или аддитивной свертки из подмножества недоминируемых политик выбирается итоговое решение рассматриваемой задачи.
Используя метод уступок и положив допустимый уровень потерь суммарной прибыли 0,8% по сравнению с теоретически максимальным, найдем итоговое решение рассматриваемой задачи, которому соответствует одна замена машины в 12-м году планового периода. Тот же результат может быть получен методом аддитивной свертки, если весовой коэффициент a1 для первого критерия (суммарной прибыли) находится в диапазоне от 0,95 до 0,47; соответственно весовой коэффициент a2 для второго критерия (объема инвестиций) изменяется от 0,05 до 0,53. При a1 > 0,95 итоговым решением является теоретически оптимальная политика замены машины для однокритериальной задачи: замена машины в 8-м и 15-м годах планового периода. При a1 < 0,47 оптимальной политике соответствует отказ от замены машины на протяжении всего планового периода.
Понятие экономико-математической модели производственной системы. Задача и методы.
Экономико-математические методы и модели (ЭММиМ) предназначены для поиска и обоснования путей повышения эффективности производства, рационального использования ресурсов, обеспечения конкурентоспособности предприятий в условиях рыночной экономики. На основе ЭММиМ с помощью современных компьютерных технологий получают данные для анализа эффективности производственных систем, прогнозирования их поведения при возможных изменениях производственной ситуации и выработки управленческих решений для достижения поставленных целей.
 Экономико-математической модель – это формализованное (математическое) описание условий и результатов функционирования производственной системы с позиций экономики. Модель строится с помощью переменных, параметров, множеств, функций, уравнений, неравенств, логических правил.
Экономико-математической модель – это формализованное (математическое) описание условий и результатов функционирования производственной системы с позиций экономики. Модель строится с помощью переменных, параметров, множеств, функций, уравнений, неравенств, логических правил.
 Найти max (min)
Найти max (min)
при условиях


 где f, gi , - заданные, в общем случае нелинейные функции n переменных -
где f, gi , - заданные, в общем случае нелинейные функции n переменных -
bi – заданные параметры.
 Запись означает, что может иметь место неравенство вида, уравнение или неравенство вида.
Запись означает, что может иметь место неравенство вида, уравнение или неравенство вида.
В экономических приложениях функцию f называют целевой функцией.
Если f и gi , - линейные функции, то имеет место задача линейного программирования.



 Экономико-математической модель – это формализованное (математическое) описание условий и результатов функционирования производственной системы с позиций экономики. Модель строится с помощью переменных, параметров, множеств, функций, уравнений, неравенств, логических правил.
Экономико-математической модель – это формализованное (математическое) описание условий и результатов функционирования производственной системы с позиций экономики. Модель строится с помощью переменных, параметров, множеств, функций, уравнений, неравенств, логических правил. Найти max (min)
Найти max (min) 


 где f, gi , - заданные, в общем случае нелинейные функции n переменных -
где f, gi , - заданные, в общем случае нелинейные функции n переменных - 
 Знаки неравенств основных ограничений двойственной задачи противоположны знакам неравенств основных ограничений исходной задачи; если исходная задача - на максимум, то двойственная к ней - на минимум и, наоборот.
Знаки неравенств основных ограничений двойственной задачи противоположны знакам неравенств основных ограничений исходной задачи; если исходная задача - на максимум, то двойственная к ней - на минимум и, наоборот. 
 Найти min z = max f =
Найти min z = max f =  Теоремы двойственности устанавливают взаимосвязь между оптимальными решениями прямой и двойственной задач.
Теоремы двойственности устанавливают взаимосвязь между оптимальными решениями прямой и двойственной задач. 
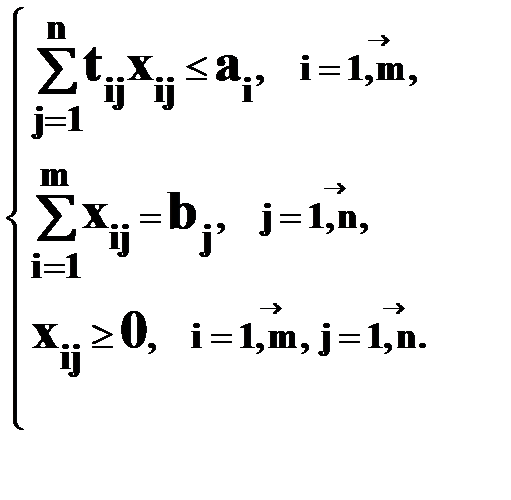 при условиях
при условиях Найти min f =
Найти min f = при условиях
при условиях

 Найти max f =
Найти max f = при условиях
при условиях Оптимальная политика замены машины формируется из условия максимизации суммарной прибыли за весь планируемый период N с учетом затрат на замену машины (инвестиций) и определяется с помощью функциональных уравнений P.Беллмана
Оптимальная политика замены машины формируется из условия максимизации суммарной прибыли за весь планируемый период N с учетом затрат на замену машины (инвестиций) и определяется с помощью функциональных уравнений P.Беллмана Функция f полагается равной нулю для значений n ³ N+1, следовательно,
Функция f полагается равной нулю для значений n ³ N+1, следовательно,


