Транспортная задача линейного программирования
Постановка задачи
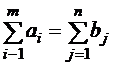 Пусть имеется m поставщиков некоторого однородного груза, сосредоточенного на станциях А 1 , А 2 , …, А m и имеется n потребителей этого продукта, расположенные на станциях В 1 , В 2 , …, Вn. Известны также запасы этого груза (а 1 , а 2 ,…, аm), которые должны быть вывезены в фиксированный период времени. Потребности получателей груза за этот же период времени составляют (b 1 , b 2 , … bn).
Пусть имеется m поставщиков некоторого однородного груза, сосредоточенного на станциях А 1 , А 2 , …, А m и имеется n потребителей этого продукта, расположенные на станциях В 1 , В 2 , …, Вn. Известны также запасы этого груза (а 1 , а 2 ,…, аm), которые должны быть вывезены в фиксированный период времени. Потребности получателей груза за этот же период времени составляют (b 1 , b 2 , … bn).
Пусть запасы равны потребностям, т.е.. (6.1)
При выполнении условия (6.1) транспортная задача называется закрытой.
Кроме того, известны затраты С ij на перевозку единицы груза с любой станции Аi на каждую станцию Вj.
Требуется составить такой план перевозок, чтобы весь груз был вывезен, все потребности были удовлетворены, а суммарные затраты на перевозки были минимальны.
Математическая модель
Обозначим величину перевозки со станции Аi на станцию Bj как xij. Тогда условия полного вывоза груза со всех станций Аi можно записать в виде системы уравнений:
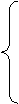
 (6.2)
(6.2)
С другой стороны, станции Вj должны получить необходимое количество груза, что тоже записывается в виде системы уравнений:

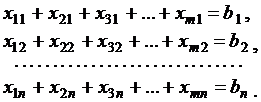 (6.3)
(6.3)
При этом выполняется условие неотрицательности для переменных xij: 
Функция цели задачи по критерию минимума суммарных затрат –
 (6.4)
(6.4)
Таким образом, транспортная задача представляет собой основную задачу линейного программирования.
Методом искусственного базиса можно привести эту задачу к каноническому виду и затем решить ее симплекс-методом. Ввиду того, что число переменных транспортной задачи велико и, при этом на любом плане число свободных переменных также велико, то симплекс метод является чрезмерно громоздким и малоэффективным. В связи с этим были разработаны специальные методы решения транспортных задач.
Вся исходная информация для транспортной задачи организуется в виде матрицы или таблицы (здесь для краткости рассмотрена задача размерности  ), в которую заносится опорный план задачи. В этой же таблице проводится оптимизация плана и записывается решение задачи
), в которую заносится опорный план задачи. В этой же таблице проводится оптимизация плана и записывается решение задачи
|
| B 1
| B 2
| B 3
| B 4
| B 5
| Запасы
|
| А1
| c 11
x 11
| c 12
x 12
| c 13
x 13
| c 14
x 14
| c 15
x 15
| a 1
|
| А 2
| c 21
x 21
| c 22
x 22
| c 23
x 23
| c 24
x 24
| c 25
x 25
| a 2
|
| А 3
| c 31
x 31
| c 32
x 32
| c 33
x 33
| c 34
x 34
| c 35
x 35
| a 3
|
| Потребности
| b 1
| b 2
| b 3
| b 4
| b 5
|
|
Рассмотрим различные методы нахождения первого опорного решения.
6.2. Методы определения начального опорного плана
Метод северо-западного угла
В соответствии с этим методом, в верхнюю левую (северо-западную) клетку таблицы заносится максимально допустимая перевозка. При этом либо вывозится весь груз со станции А 1, тогда все остальные клетки первой строки вычеркиваются, либо потребности первого потребителя В 1 полностью удовлетворены, тогда все клетки первого столбца вычеркиваются. После этого самой северо-западной клеткой становится клетка А1-В2 или А2-В1. Указанный алгоритм применяется до заполнения всей таблицы.
Рассмотрим этот метода на примере.
Ставим первую перевозку в клетку А1-В1. Она будет равна  . Закрыт первый столбец. Идем по строке. В клетку А1-В2 ставим перевозку, равную
. Закрыт первый столбец. Идем по строке. В клетку А1-В2 ставим перевозку, равную  . Закрыли первую строку (в закрытой строке или столбце будем ставить прочерки для того, чтобы не поставить туда перевозку). Спускаемся по второму столбцу. В клетку А2-В2 ставим перевозку
. Закрыли первую строку (в закрытой строке или столбце будем ставить прочерки для того, чтобы не поставить туда перевозку). Спускаемся по второму столбцу. В клетку А2-В2 ставим перевозку  и закрываем второй столбец. Идем по второй строке и ставим перевозку в клетку А2-В3. Она равна
и закрываем второй столбец. Идем по второй строке и ставим перевозку в клетку А2-В3. Она равна  . Закрыли третий столбец. Продолжаем идти по третьей строке. В клетку А2-В4 ставим перевозку
. Закрыли третий столбец. Продолжаем идти по третьей строке. В клетку А2-В4 ставим перевозку  . Теперь закрыли вторую строку и спускаемся по четвертому столбцу. В клетку А3-В4 ставим перевозку
. Теперь закрыли вторую строку и спускаемся по четвертому столбцу. В клетку А3-В4 ставим перевозку  . Закрыв этот столбец, идем по третьей строке. Перевозка в клетке А3-В5 равна
. Закрыв этот столбец, идем по третьей строке. Перевозка в клетке А3-В5 равна  . Таблица исчерпана. Все грузы вывезены, все потребности удовлетворены.
. Таблица исчерпана. Все грузы вывезены, все потребности удовлетворены.
Недостатком данного метода является то, что он не учитывает стоимость перевозок и поэтому, как правило, получаемый план далек от оптимального.
|
| В 1
| В 2
| В 3
| В 4
| В 5
|
|
| А 1
| 20 4
| 20 3
| - 4
| - 11
| - 9
|
|
| А 2
| - 3
| 1 4
| 7 7
| 22 15
| - 8
|
|
| А 3
| - 7
| - 4
| - 2
| 2 8
| 8 15
|
|
|
|
|
|
|
|
|
|
Вычислим стоимость всех перевозок. Она равна:

Теперь на этом же примере рассмотрим другой метод.
Метод наименьшей стоимости
Метод наименьшей стоимости учитывает в какой-то мере затраты на перевозки и строится следующим образом: рассматривается матрица, находится клетка с наименьшей стоимостью, в которую заносится максимально допустимая перевозка. При этом вычеркивается либо строка, либо столбец, затем в остающейся части таблицы находится клетка с наименьшей стоимостью и т. д.
Опишем последовательность действий для данного метода на примере.
Выбираем в таблице клетку с наименьшей стоимостью (А3-В3) и ставим в нее перевозку  , закрыли третий столбец. В пункте А 3 осталось 10-7=3 единиц груза. В оставшихся клетках выбираем наименьшую стоимость. Таких клеток две: А2-В1 и А1-В2. Случайным образом выбираем сначала клетку А1-В2: ставим сюда перевозку, равную
, закрыли третий столбец. В пункте А 3 осталось 10-7=3 единиц груза. В оставшихся клетках выбираем наименьшую стоимость. Таких клеток две: А2-В1 и А1-В2. Случайным образом выбираем сначала клетку А1-В2: ставим сюда перевозку, равную  . Мы закрыли второй столбец, а в пункте А1 осталось 40-21=19 единиц груза. Далее ставим перевозку в клетку А2-В1. Она равна
. Мы закрыли второй столбец, а в пункте А1 осталось 40-21=19 единиц груза. Далее ставим перевозку в клетку А2-В1. Она равна  . Закрыли первый столбец, а в пункте А 2 осталось 30-20=10 единиц груза. Минимальная стоимость в оставшихся клетках равна 8 и находится она в клетке А3-В4. Ставим туда перевозку
. Закрыли первый столбец, а в пункте А 2 осталось 30-20=10 единиц груза. Минимальная стоимость в оставшихся клетках равна 8 и находится она в клетке А3-В4. Ставим туда перевозку  . Закрыта третья строка.
. Закрыта третья строка.
Пункту В 4 необходимо еще 24-3=21 единиц груза. Такая же стоимость и в клетке А2-В5. Ставим туда перевозку  . Закрыли пятый столбец, а в пункте А 2осталось 10-8=2 ед. груза. Во второй строке осталась свободной только клетка А2-В4. Ставим туда перевозку
. Закрыли пятый столбец, а в пункте А 2осталось 10-8=2 ед. груза. Во второй строке осталась свободной только клетка А2-В4. Ставим туда перевозку  . Вторая строка закрыта.
. Вторая строка закрыта.
Пункту В 4 необходимо 21-2=19 единиц груза. Заполняем оставшуюся клетку А1-В4. Ставим сюда перевозку 19 единиц груза. Заполнена вся таблица.
В большинстве случаев этот метод дает план, который ближе к оптималь2ому, однако, во всех случаях требуется сравнивать величины функции цели на получаемых планах и выбирать тот, для которого функция принимает наименьшее значение.
|
| В 1
| В 2
| В 3
| В 4
| В 5
|
|
| А 1
| - 4
| 21 3
| - 4
| 19 11
| - 9
|
|
| А 2
| 20 3
| - 4
| - 7
| 2 15
| 8 8
|
|
| А 3
| - 7
| - 4
| 7 2
| 3 8
| - 15
|
|
|
|
|
|
|
|
|
|
Вычислим общую стоимость перевозок:
 .
.
Метод двойного предпочтения
В данном методе отмечаются клетки с наименьшей стоимостью в каждой строке, затем выбирается наименьший элемент в столбце. Отметим их каким-нибудь значком. В дважды отмеченные клетки ☺☺ заносятся максимально допустимые перевозки. Далее, в отмеченные один раз клетки ☺ заносятся максимальные перевозки. Остаток таблицы можно заполнить методом северо-западного угла или методом наименьшей стоимости.
Опишем алгоритм этого метода на том же примере.
Выберем в каждом столбце минимальную стоимость и отметим его значком. Тоже сделаем со строками. Выбрали клетки с двумя значками: в клетку А1-В2 ставим перевозку  (закрыт 2 столбец, в пункте А 1 осталось 40-21=19 ед.); клетка А2-В1 – перевозка равна
(закрыт 2 столбец, в пункте А 1 осталось 40-21=19 ед.); клетка А2-В1 – перевозка равна  , закрыт 1 столбец, в пункте А 2 осталось 30-20=10 ед.); клетка А3-В3 – перевозка
, закрыт 1 столбец, в пункте А 2 осталось 30-20=10 ед.); клетка А3-В3 – перевозка  , закрыт 3 столбец, в пункте А 2 осталось 10-7=3 ед.) Теперь ставим перевозки в клетки с одним значком: А2-В5 – перевозка
, закрыт 3 столбец, в пункте А 2 осталось 10-7=3 ед.) Теперь ставим перевозки в клетки с одним значком: А2-В5 – перевозка 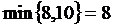 (закрыт 5 столбец, в пункте А 2 осталось 10-8=2 ед.); А3-В4 – перевозка
(закрыт 5 столбец, в пункте А 2 осталось 10-8=2 ед.); А3-В4 – перевозка  (закрыта 3 строка, а пункту В 4 нужно 24-3=21 ед.). Остальные клетки можно заполнить так же, как в предыдущем методе.
(закрыта 3 строка, а пункту В 4 нужно 24-3=21 ед.). Остальные клетки можно заполнить так же, как в предыдущем методе.
|
| В 1
| В 2
| В 3
| В 4
| В 5
|
|
| А 1
| - 4
| ☺☺21 3
| - 4
| 19 11
| - 9
|
|
| А 2
| ☺☺20 3
| - 4
| - 7
| 2 15
| ☺8 8
|
|
| А 3
| - 7
| - 4
| ☺☺7 2
| ☺ 3 8
| - 15
|
|
|
|
|
|
|
|
|
|
Общая стоимость перевозок равна:
 .
.
Для нашего примера опорные планы двух последних методов совпадают. Выберем метод двойного предпочтения и оценим его на оптимальность по методу потенциалов.
Метод потенциалов
Метод потенциалов позволяет оценить составленный опорный план и при необходимости, последовательно улучшая его, находить оптимальное решение.
Теоремы метода.
Теорема 1: Если опорный план X = (xij) является оптимальным, то существует система из (m+n) чисел, называемых потенциалами, Ui, Vj, такая, что:
а) Ui +Vj = Cij, для xij > 0 (базисные переменные);
б) Ui +Vj = Cij, для xij = 0 (свободные переменные).
Таким образом, для оптимальности опорного плана необходимо выполнение следующих условий:
- для каждой занятой клетки сумма потенциалов равна стоимости перевозки единицы груза, стоящей в этой клетке:
Ui +Vj = Cij (6.5)
- для каждой свободной клетки сумма потенциалов меньше или равна стоимости перевозки единицы груза, стоящей в этой клетке:
Ui +Vj ≤ Cij (6.6)
Примечание: Система (6.5) содержит (m+n) неизвестных и (m+n- 1 ) линейно независимых уравнений. Такая система имеет бесчисленное множество решений, которые можно получить, придавая одной из неизвестных конкретное значение. Это значение выбирается произвольно, например, можно придать U1 значение равное 0, тогда другие потенциалы вычисляются из системы (6.5).
Теорема 2. Любая закрытая транспортная задача имеет решение, которое достигается за конечное число шагов метода потенциалов.



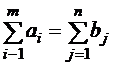 Пусть имеется m поставщиков некоторого однородного груза, сосредоточенного на станциях А 1 , А 2 , …, А m и имеется n потребителей этого продукта, расположенные на станциях В 1 , В 2 , …, Вn. Известны также запасы этого груза (а 1 , а 2 ,…, аm), которые должны быть вывезены в фиксированный период времени. Потребности получателей груза за этот же период времени составляют (b 1 , b 2 , … bn).
Пусть имеется m поставщиков некоторого однородного груза, сосредоточенного на станциях А 1 , А 2 , …, А m и имеется n потребителей этого продукта, расположенные на станциях В 1 , В 2 , …, Вn. Известны также запасы этого груза (а 1 , а 2 ,…, аm), которые должны быть вывезены в фиксированный период времени. Потребности получателей груза за этот же период времени составляют (b 1 , b 2 , … bn).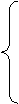
 (6.2)
(6.2)
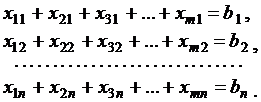 (6.3)
(6.3)
 (6.4)
(6.4) ), в которую заносится опорный план задачи. В этой же таблице проводится оптимизация плана и записывается решение задачи
), в которую заносится опорный план задачи. В этой же таблице проводится оптимизация плана и записывается решение задачи . Закрыт первый столбец. Идем по строке. В клетку А1-В2 ставим перевозку, равную
. Закрыт первый столбец. Идем по строке. В клетку А1-В2 ставим перевозку, равную  . Закрыли первую строку (в закрытой строке или столбце будем ставить прочерки для того, чтобы не поставить туда перевозку). Спускаемся по второму столбцу. В клетку А2-В2 ставим перевозку
. Закрыли первую строку (в закрытой строке или столбце будем ставить прочерки для того, чтобы не поставить туда перевозку). Спускаемся по второму столбцу. В клетку А2-В2 ставим перевозку  и закрываем второй столбец. Идем по второй строке и ставим перевозку в клетку А2-В3. Она равна
и закрываем второй столбец. Идем по второй строке и ставим перевозку в клетку А2-В3. Она равна  . Закрыли третий столбец. Продолжаем идти по третьей строке. В клетку А2-В4 ставим перевозку
. Закрыли третий столбец. Продолжаем идти по третьей строке. В клетку А2-В4 ставим перевозку  . Теперь закрыли вторую строку и спускаемся по четвертому столбцу. В клетку А3-В4 ставим перевозку
. Теперь закрыли вторую строку и спускаемся по четвертому столбцу. В клетку А3-В4 ставим перевозку  . Закрыв этот столбец, идем по третьей строке. Перевозка в клетке А3-В5 равна
. Закрыв этот столбец, идем по третьей строке. Перевозка в клетке А3-В5 равна  . Таблица исчерпана. Все грузы вывезены, все потребности удовлетворены.
. Таблица исчерпана. Все грузы вывезены, все потребности удовлетворены.
 , закрыли третий столбец. В пункте А 3 осталось 10-7=3 единиц груза. В оставшихся клетках выбираем наименьшую стоимость. Таких клеток две: А2-В1 и А1-В2. Случайным образом выбираем сначала клетку А1-В2: ставим сюда перевозку, равную
, закрыли третий столбец. В пункте А 3 осталось 10-7=3 единиц груза. В оставшихся клетках выбираем наименьшую стоимость. Таких клеток две: А2-В1 и А1-В2. Случайным образом выбираем сначала клетку А1-В2: ставим сюда перевозку, равную  . Мы закрыли второй столбец, а в пункте А1 осталось 40-21=19 единиц груза. Далее ставим перевозку в клетку А2-В1. Она равна
. Мы закрыли второй столбец, а в пункте А1 осталось 40-21=19 единиц груза. Далее ставим перевозку в клетку А2-В1. Она равна  . Закрыли первый столбец, а в пункте А 2 осталось 30-20=10 единиц груза. Минимальная стоимость в оставшихся клетках равна 8 и находится она в клетке А3-В4. Ставим туда перевозку
. Закрыли первый столбец, а в пункте А 2 осталось 30-20=10 единиц груза. Минимальная стоимость в оставшихся клетках равна 8 и находится она в клетке А3-В4. Ставим туда перевозку  . Закрыта третья строка.
. Закрыта третья строка. . Закрыли пятый столбец, а в пункте А 2осталось 10-8=2 ед. груза. Во второй строке осталась свободной только клетка А2-В4. Ставим туда перевозку
. Закрыли пятый столбец, а в пункте А 2осталось 10-8=2 ед. груза. Во второй строке осталась свободной только клетка А2-В4. Ставим туда перевозку 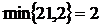 . Вторая строка закрыта.
. Вторая строка закрыта. .
. (закрыт 2 столбец, в пункте А 1 осталось 40-21=19 ед.); клетка А2-В1 – перевозка равна
(закрыт 2 столбец, в пункте А 1 осталось 40-21=19 ед.); клетка А2-В1 – перевозка равна  , закрыт 1 столбец, в пункте А 2 осталось 30-20=10 ед.); клетка А3-В3 – перевозка
, закрыт 1 столбец, в пункте А 2 осталось 30-20=10 ед.); клетка А3-В3 – перевозка  , закрыт 3 столбец, в пункте А 2 осталось 10-7=3 ед.) Теперь ставим перевозки в клетки с одним значком: А2-В5 – перевозка
, закрыт 3 столбец, в пункте А 2 осталось 10-7=3 ед.) Теперь ставим перевозки в клетки с одним значком: А2-В5 – перевозка 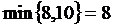 (закрыт 5 столбец, в пункте А 2 осталось 10-8=2 ед.); А3-В4 – перевозка
(закрыт 5 столбец, в пункте А 2 осталось 10-8=2 ед.); А3-В4 – перевозка  (закрыта 3 строка, а пункту В 4 нужно 24-3=21 ед.). Остальные клетки можно заполнить так же, как в предыдущем методе.
(закрыта 3 строка, а пункту В 4 нужно 24-3=21 ед.). Остальные клетки можно заполнить так же, как в предыдущем методе. .
.


