Линейная независимость лестничной системы векторов.

Неравенство Коши-Буняковского.

Для любых двух векторов в евклидовом пространстве справедливо неравенство

Доказательство:

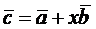, x-произвольное число

по свойству положительной определенности скалярного произведения

 

Неравенство треугольника.

Каковы бы ни были три точки, расстояние между любыми двумя из этих точек не больше суммы расстояний от них до третьей.

Доказательство. Пусть A, B и С – данные три точки. Если две токи из трех или все три точки совпадают, то утверждение теоремы очевидно. Если все точки различны и лежат на одной прямой, то AB + BC = AC. Отсюда видно, что каждое из трех расстояний не больше суммы двух других. Если три точки не лежат на одной прямой докажем, что AC< доказана. Теорема ВС. + AB AC то BC, DC и AD как Так DC. ≤ доказанному По AC. прямую на BD перпендикуляр Опустим>

 

Линейная независимость лестничной системы векторов.

Система векторов в Rn:

= (a1, a2, a3 … an)

= (0, b2, b3 … bn)

= (0, 0, c3 … cn)

Теорема: любая лестничная система векторов линейно независима.

Доказательство: Предположим противное. Тогда один из данных векторов должен линейно выражаться через остальные. Пусть, например, линейно выражается через , …

=k +l …

Но такое равенство невозможно, поскольку первая координата вектора отлична от нуля, а первая координата вектора k +l … равно нулю. Полученное противоречие доказывает, что система , , , … линейно независима.

 

Однозначность разложения вектора по базису.

Теорема о базисе. Любая ЛНЗ система векторов из Rⁿ явл. базисом Rⁿ, когда число векторов этой системы равно n.

Док-во. Пусть: { в₁, в₂, …, в_m } ЛНЗ система в Rⁿ, докажем, что m=n 1) m>n. Получим, что система ЛЗ(по теореме об ортогональном векторе), что противоречит условию; 2) m<n Пусть{ в₁, в₂, …, в_m }- базис Rⁿ, то для любого Х ЄRⁿ х=х₁в₁+х₂в₂+…+х_mв_m; m<n,то по теореме о существовании ортогонального вектора есть ненулевой вектор, кот. Ортогонален любому вектору этой системы (у_╨в_i, i=1,…,n), то ув_i=0; у ЄRⁿ, тогда у=у₁в₁+у₂в₂+…+у_mв_m, умножим это рав-во на само себя уу=(у₁в₁+у₂в₂+…+у_mв_m)у=у₁(в₁у₁)+у₂(у₂в₂)+…+у_m(у_mв_m)=0; уу=0, то у=0, а по усл теоремы у≠0, противоречие, значит m<n неверно, тогда m=n.
5. Формула умножения комплексных чисел в тригонометрической форме.

Z₁=| Z₁|(cosφ₁ + i sinφ₁); Z₂=| Z₂|(cosφ₂ + i sinφ₂)

Z₁ · Z₂ =| Z₁|| Z₂|((cosφ₁ cosφ₂ - sinφ₁ sinφ₂ ) + i(sinφ₁ cosφ₂ + cosφ₁ sinφ₂)) =

| Z₁|| Z₂|(cos(φ₁+ φ₂) + i sin(φ₁ + φ₂));

Для умножения Z₁ на Z₂ модули этих чисел следует перемножить, а аргументы сложить.

 

 

Формула деления комплексных чисел в тригонометрической форме.

Z₁=| Z₁|(cosφ₁ + i sinφ₁); Z₂=| Z₂|(cosφ₂ + i sinφ₂)

φ₁-φ₂) + isin (φ₁-φ₂)) Z₂≠0

Для нахождения частного следует модуль числа Z₁ разделить на модуль числа Z₂, а из аргумента числа Z₁ вычесть аргумент числа Z₂.

 

Неравенство Коши-Буняковского.

Для любых двух векторов в евклидовом пространстве справедливо неравенство

Доказательство:

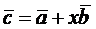, x-произвольное число

по свойству положительной определенности скалярного произведения

 

Неравенство треугольника.

Каковы бы ни были три точки, расстояние между любыми двумя из этих точек не больше суммы расстояний от них до третьей.

Доказательство. Пусть A, B и С – данные три точки. Если две токи из трех или все три точки совпадают, то утверждение теоремы очевидно. Если все точки различны и лежат на одной прямой, то AB + BC = AC. Отсюда видно, что каждое из трех расстояний не больше суммы двух других. Если три точки не лежат на одной прямой докажем, что AC< доказана. Теорема ВС. + AB AC то BC, DC и AD как Так DC. ≤ доказанному По AC. прямую на BD перпендикуляр Опустим>

 

Линейная независимость лестничной системы векторов.

Система векторов в Rn:

= (a1, a2, a3 … an)

= (0, b2, b3 … bn)

= (0, 0, c3 … cn)

Теорема: любая лестничная система векторов линейно независима.

Доказательство: Предположим противное. Тогда один из данных векторов должен линейно выражаться через остальные. Пусть, например, линейно выражается через , …

=k +l …

Но такое равенство невозможно, поскольку первая координата вектора отлична от нуля, а первая координата вектора k +l … равно нулю. Полученное противоречие доказывает, что система , , , … линейно независима.