
При сложении цифры суммируются по разрядам, и если при этом возникает избыток, то он переносится влево.
Пример 2.1
Сложим числа 15 и 6 в различных системах счисления.
| Десятичная: 1510+610
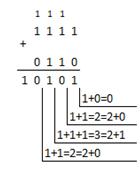
| Двоичная: 11112+1112
| Восьмеричная: 178+68
|
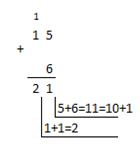
| 
| 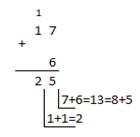
|
| | Шестнадцатеричная: F16+616

| Ответ:
15+6 = 2110 = 101012 = 258 = 1516.
Проверка. Преобразуем полученные суммы к десятичному виду:
101012 = 24 + 22 + 20 = 16+4+1=21,
258 = 2*81 + 5*80 = 16 + 5 = 21,
1516 = 1*161 + 5*160 = 16+5 = 21.
| |
| | | | | | |
Пример 2.2 Сложим числа 15, 7 и 3.
| Десятичная: 1510+710+310
| Двоичная: 11112+1112+112
| Восьмеричная: 178+78+38
|
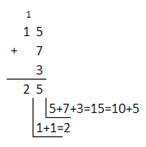
| 
| 
|
Шестнадцатеричная:
F16+716+316

| Ответ:
15+7+3 = 2510 = 110012 = 318 = 1916. Проверка:
110012 = 24 + 23 + 20 = 16+8+1=25,
318 = 3*81 + 1*80 = 24 + 1 = 25,
1916 = 1*161 + 9*160 = 16+9 = 25.
|
Пример 2.3 Сложим числа 141,5 и 59,75.
| Десятичная: 141,510+59,7510
| Двоичная: 10001101,12+111011,112
|

| 
|
| Восьмеричная: 215,48+73,68
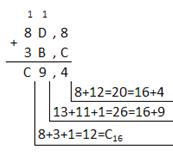
| Шестнадцатеричная: 8D,816+3B,C16
|
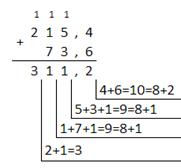
| 
|
Ответ: 141,5 + 59,75 = 201,2510 = 11001001,012 = 311,28 = C9,416
Проверка. Преобразуем полученные суммы к десятичному виду:
11001001,012 = 27 + 26 + 23 + 20 + 2-2 = 201,25
311,28 = 3 * 82 + 1*81 + 1 * 80 + 2 . 8-1 = 201,25
C9,416 = 12 * 161 + 9 * 160 + 4 * 16-1 = 201,25
Пример 2.4 Сложить двоичные числа 11012 и 110112.
Запишем слагаемые в столбик и пронумеруем разряды, присвоив младшему разряду номер 1:
номера разрядов: 5 4 3 2 1
+ 1 1 0 12
1 1 0 1 12
Процесс образования результата по разрядам описан ниже:
а) разряд 1 формируется следующим образом: 12 + 12 = 102; 0 остается в разряде 1, 1 переносится во второй разряд;
б) разряд 2 формируется следующим образом: 02 + 12 + 12 = 102, где вторая 12 – единица переноса; 0 остается в разряде 2, 1 переносится в третий разряд;
в) третий разряд формируется следующим образом: 12 + 02 + 12 = 102, где вторая 12 – единица переноса; 0 остается в разряде 3, 1 переносится в разряд 4;
г) четвертый разряд формируется следующим образом: 12 + 12 + 12 = 112, где третья 12 – единица переноса; 1остается в разряде 4, 1 переносится в пятый разряд;
д) пятый разряд формируется следующим образом: 12 + 12 = 102; где вторая 12 – единица переноса; 0 остается в разряде 5, 1 переносится в шестой разряд.
Таким образом:
+ 1 1 0 12
 1 1 0 1 12
1 1 0 1 12
10 1 0 0 02.
Проверим результат. Для этого определим полные значения слагаемых и результата:
11012 = 1*23 +1*22 + 0*21 + 1*20 = 8 + 4 + 1 = 13;
110112 = 1*24 + 1*23 + 0*22 + 1*21 + 1*20 = 16 + 8 + 2 + 1 = 27;
1010002 = 1*25 + 0*24 + 1*23 + 0*22 + 0*21 + 0*20 = 32 + 8 = 40.
Поскольку 13 + 27 = 40, двоичное сложение выполнено верно.
Пример 2.5 Сложить шестнадцатеричные числа 1С16 и 7В16.
Запишем слагаемые в столбик и пронумеруем разряды, присвоив младшему разряду номер 1:
номера разрядов: 2 1
+ 1 С16
7 В16
Процесс образования результата по разрядам описан ниже (он включает преобразование в процессе сложения каждой шестнадцатеричной цифры в десятичное число и обратные действия):
а) разряд 1 формируется следующим образом: С16 + В16 = 12 + 11 = 23 = 1716; 7 остается в разряде 1; 1 переносится в разряд 2;
б) разряд 2 формируется следующим образом: 116 + 716 + 116 = 916, где вторая 116 – единица переноса.
Таким образом:
+ 1 С16
 7 В16
7 В16
9 716.
Проверим результат. Для этого определим полные значения слагаемых и результата:
1С16 = 1*161 + 12*160 = 16 + 12 = 28;
7В16 = 7*161 + 11*160 = 112 + 11 = 123;
9716 = 9*161 + 7*160 = 144 + 7 = 151.
Поскольку 28 + 123 = 151, сложение выполнено верно.
Вычитание
Пример 2.6 Вычтем единицу из чисел 102, 108 и 1016
| Двоичная:
102-12
| Восьмеричная:
108-18
| Шестнадцатеричная:
1016-116
|

| 
| 
|
Пример 2.7
Вычтем единицу из чисел 1002, 1008 и 10016.
| Двоичная:
1002-12
| Восьмеричная:
1008-18
| Шестнадцатеричная:
10016-116
|

| 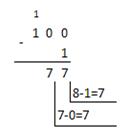
| 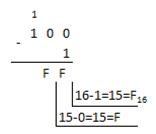
|
Пример 2.8 Вычтем число 59,75 из числа 201,25.
| Десятичная:
201,252– 59,752
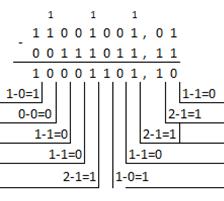
| Двоичная:
11001001,012 – 111011,112
|
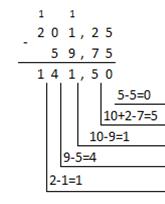
| 
|
| Восьмеричная:
311,28 – 73,68
| Шестнадцатеричная:
С9,416– 3В,С16
|

| 
|
Ответ: 201,2510 - 59,7510 = 141,510 = 10001101,12 = 215,48 = 8D,816.
Проверка. Преобразуем полученные разности к десятичному виду:
10001101,12 = 27 + 23 + 22 + 20 + 2-1 = 141,5;
215,48 = 2 * 82 + 1 * 81 + 5 * 80 + 4 * 8-1 = 141,5;
8D,816 = 8 * 161 + D * 160 + 8 * 16-1 = 141,5.
Пример 2.9 Вычесть из двоичного числа 1012 двоичное число 112.
Запишем алгебраические слагаемые в столбик в порядке «уменьшаемое – вычитаемое» и пронумеруем разряды, присвоив младшему разряду номер 1:
номера разрядов: 3 2 1
- 1 0 12
1 12
Процесс образования результата по разрядам описан ниже:
а) разряд 1 формируется следующим образом: 12 – 12 = 02;
б) разряд 2 формируется следующим образом: поскольку 0 < 1 и непосредственное вычитание невозможно, занимаем для уменьшаемого единицу в старшем разряде 3. Тогда разряд 2 рассчитывается как 102 – 12 = 12;
в) третий разряд формируется следующим образом: поскольку единица была занята в предыдущем шаге, в разряде остался 0.
Таким образом:
- 1 0 12
 1 12
1 12
1 02.
Проверим результат. Для этого определим полные значения слагаемых и результата. Имеем:
1012 = 5; 112 = 3; 102 = 2.
Поскольку 5 – 3 = 2, вычитание выполнено верно.
Пример 2.10 Вычесть из шестнадцатеричного числа 9716 шестнадцатеричное число 7В16.
Запишем алгебраические слагаемые в столбик в порядке «уменьшаемое – вычитаемое» и пронумеруем разряды, присвоив младшему разряду номер 1:
номера разрядов: 2 1
- 9 716
7 В16
Процесс образования результата по разрядам описан ниже:
а) разряд 1 формируется следующим образом: поскольку 716< В16 и непосредственное вычитание невозможно, занимаем для уменьшаемого единицу в старшем разряде 2. Тогда 1716 – В16 = 23 – 11 = 12 = С16;
б) разряд 2 формируется следующим образом: поскольку единица была занята в предыдущем шаге, разряд 2 уменьшаемого стал равным 816. Тогда разряд 2 рассчитывается как 816 – 716 = 116.
Таким образом:
- 9 716
 7 В16
7 В16
1 С16.
Для проверки результата используем данные из примера 3.17.
Таким образом, вычитание выполнено верно.
Умножение
Выполняя умножение многозначных чисел в различных позиционных системах счисления, можно использовать обычный алгоритм перемножения чисел в столбик, но при этом результаты перемножения и сложения однозначных чисел необходимо заимствовать из соответствующих рассматриваемой системе таблиц умножения и сложения.
Умножение в двоичной системе

| Умножение в восьмеричной системе

|
Ввиду чрезвычайной простоты таблицы умножения в двоичной системе, умножение сводится лишь к сдвигам множимого и сложениям.
Пример 2.11 Перемножим числа 5 и 6.
| Десятичная: 510*610
| Двоичная: 1012*1102
| Восьмеричная: 58*68
|
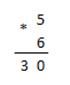
| 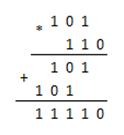
| 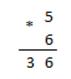
|
Ответ: 5*6 = 3010 = 111102 = 368.
Проверка. Преобразуем полученные произведения к десятичному виду:
111102 = 24 + 23 + 22 + 21 = 30;
368 = 3*81 + 6*80 = 30.
Пример 2.12 Перемножим числа 115 и 51.
| Десятичная:
11510*5110
| Двоичная:
11100112*1100112
| Восьмеричная:
1638*638
|
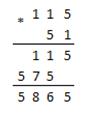
| 
| 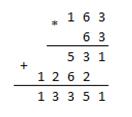
|
Ответ: 115*51 = 586510 = 10110111010012 = 133518.
Проверка. Преобразуем полученные произведения к десятичному виду:
10110111010012 = 212 + 210 + 29 + 27 + 26 + 25 + 23 + 20 = 5865;
133518 = 1*84 + 3*83 + 3*82 + 5*81 + 1*80 = 5865
Пример 2.13 Умножить двоичное число 1012 на двоичное число 112.
Запишем множители в столбик и пронумеруем разряды, присвоив младшему разряду номер 1:
номера разрядов: 3 2 1
* 1 0 12
1 12
Процесс образования результата по шагам умножения множимого на каждый разряд множителя с последующим сложением показан ниже:
а) умножение множимого на разряд 1 множителя дает результат: 1012 * 12 = 1012;
б) умножение множимого на разряд 2 множителя дает результат: 1012 * 102 = 10102. Здесь значение разряда 2 множителя сформировано по принципам формирования значения числа в позиционных системах счисления;
в) для получения окончательного результата складываем результаты предыдущих шагов: 1012 + 10102 = 11112.
Для проверки результата найдем полное значение сомножителей и произведения (см. табл. 3.1):
1012 = 5; 112 = 3; 11112 = 15.
Поскольку 5 * 3 = 15, умножение выполнено верно: 1012 * 112 = 11112.
Пимер 2.14 Умножить шестнадцатеричное число 1С16 на шестнадцатеричное число 7В16.
Запишем множители в столбик и пронумеруем разряды, присвоив младшему разряду номер 1:
номера разрядов: 2 1
* 1 С16
7 В16
Процесс образования результата по шагам умножения множимого на каждый разряд множителя с последующим сложением показан ниже (в процессе умножения выполняем перевод шестнадцатеричных чисел в десятичные и обратно):
а) умножение множимого на разряд 1 множителя дает результат: 1С16 * В16 = 28 * 11 = 308 = 13416;
б) умножение множимого на разряд 2 множителя дает результат: 1С16 * 706 = 28 * 112 = 3136 = С4016. Здесь значение разряда 2 множителя сформировано по принципам формирования значения числа в позиционных системах счисления;
в) для получения окончательного результата складываем результаты предыдущих шагов: 13416 + С4016 = D7416.
Для проверки результата найдем полное значение сомножителей и произведения, воспользовавшись результатами примера 3.17 и правилами формирования полного значения числа:
1С16 = 28; 7В16 = 123;
D7416 = 13*162 + 7*161 + 4*160 = 3444.
Поскольку 28 * 123 = 3444, умножение выполнено верно: 1С16 * 7В16 = D7416.
Деление
Деление в любой позиционной системе счисления производится по тем же правилам, как и деление углом в десятичной системе. В двоичной системе деление выполняется особенно просто, ведь очередная цифра частного может быть только нулем или единицей.
Пример 2.15 Разделим число 30 на число 6.
| Десятичная:
3010: 610
| Двоичная:
111102: 1102
| Восьмеричная:
368: 68
|

| 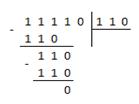
| 
|
Ответ: 30: 6 = 510 = 1012 = 58.
Пример 2.16 Разделим число 5865 на число 115.
| Десятичная:
586510: 11510
| Двоичная:
10110111010012: 11100112
| Восьмеричная:
1335188: 1638
|

| 
| 
|
Ответ: 5865: 115 = 5110 = 1100112 = 638.
Проверка. Преобразуем полученные частные к десятичному виду:
1100112 = 25 + 24 + 21 + 20 = 51;
638 = 6*81 + 3*80 = 51.
Пример 2.17 Разделим число 35 на число 14.
| Десятичная:
3510: 1410
| Двоичная:
1000112: 11102
| Восьмеричная:
438: 168
|

| 
| 
|
Ответ: 35: 14 = 2,510 = 10,12 = 2,48.
Проверка. Преобразуем полученные частные к десятичному виду:
10,12 = 21 + 2 -1 = 2,5;
2,48 = 2*80 + 4*8-1 = 2,5.
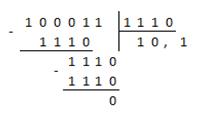
Пример 2.18 Разделить двоичное число 11112 на двоичное число 112.
 Решение задачи представим схемой:
Решение задачи представим схемой:
-11112 112

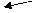
 112 1012
112 1012
 -0112
-0112
 112
112
02
Для проверки правильности результата воспользуемся данными из примера 3.20. Они показывают, что деление выполнено верно: 11112 / 112 = 1012.
Задания для самостоятельного выполнения
Выполните сложение:
| Двоичная система счисления
а)10011(2)+1011(2);
б) 110010,101(2)+1011010011,01(2);
в)1000001101(2)+1100101000(2);
г)1100111,00101(2)+101010110,011(2);
| Восьмеричная и шестнадцатеричная системы счисления
а) 764(8)+ 365(8);
б) 14(8)+ 8(8) + 4(8);
в) 38,D(16)+8C,B(16);
г)E(16)+6(16) + F(16).
|
Выполните вычитание:
| Двоичная система счисления
а) 1101000101(2)-111111000(2);
б)1011101011,001(2)-1011001000,01001(2);
в) 1010110010(2)-1000000000(2);
г) 1101001010,101(2)-1100111000,011(2).
| Восьмеричная и шестнадцатеричная системы счисления
а)2025,2(8) - 131,2((8);
б) 137(8)- 64(8);
в) 2D8,4(16)- А3,B(16);
г)416,3(16)- 255,3(16).
|
Выполните умножение:
| Двоичная система счисления
а)1100110(2)* 1011010(2);
б) 1101101,01(2)* 101010,001(2);
в) 10101,111(2)* 11010(2);
г) 11001,11110(2)* 1011100,1(2).
| Восьмеричная и шестнадцатеричная системы счисления
а)1723,2(8)*15,2 ((8);
б)2001,6 (8)*125,2 (8);
в) 54,3( (16)*9,6 (16);
г)2C,4 (16)*12,98 (16).
|
Выполните деление:
| Двоичная система счисления
а)1111(2): 101(2);
б) 1100,011(2): 10,01(2);
в) 1111(2): 100(2);
г) 1001011(2): 101(2).
| Восьмеричная и шестнадцатеричная системы счисления
а) 571(8): 8((8);
б) 174(8): 14((8);
в) 7467(16): 16(16);
г)В3(16): 16(16).
|
Примечание. Проверьте правильность вычислений переводом исходных данных и результатов в десятичную систему счисления.
Глава 3






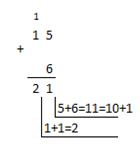


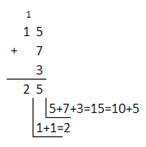





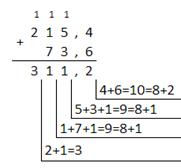

 1 1 0 1 12
1 1 0 1 12 7 В16
7 В16



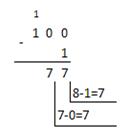
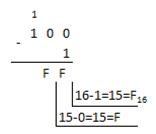
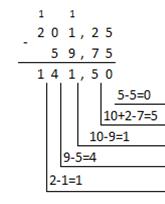



 1 12
1 12 7 В16
7 В16

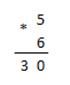
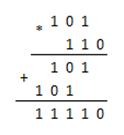
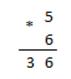
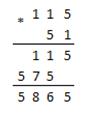

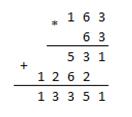

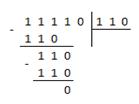







 Решение задачи представим схемой:
Решение задачи представим схемой:
 112 1012
112 1012 -0112
-0112


