Их числовые характеристики
Биномиальное распределение
СВ Х распределена по биномиальному закону, если она принимает значения 0, 1, 2, …, n, а соответствующие вероятности вычисляются по формуле Бернулли:
 , (5.1
, (5.1
где 0 < p < 1, q=1 - p, k=0, 1, 2, …, n.
Такая СВ выражает число появлений события А в п независимых испытаниях, проводимых в одинаковых условиях.
| Ряд распределения имеет вид:
|
| хi=k
|
|
| …
| i
|
| n
|
| P(X=k)
| 
| 
|
| 
|
| 
|
А числовые характеристики равны:
 D[X]=npq.
D[X]=npq.
Пример Три конкурирующие фирмы работают независимо друг от друга. Вероятность обанкротиться для каждой из них равна 0.1. Составить закон распределения СВ Х – числа обанкротившихся фирм. Найти математическое ожидание и дисперсию Х.
4Дискретная СВ X - число обанкротившихся фирм имеет следующие возможные значения: x 1=0 (ни одна фирма не обанкротилась), x 2=1 (обанкротилась одна фирма), x 3=2 (две обанкротились) и x 4=3(обанкротились все три). Банкротства фирм независимы друг от друга, поэтому применима формула Бернулли (n =3, k =0, 1, 2, 3; p =0,1, q =1 ‑ 0,1= 0,9), следовательно,
P(X= 0 ) = P 3 ( 0 ) = q 3=0,93=0,729; P(X =1 ) = P 3 ( 1 ) =  pq 2=3´0,1´0,9=0,243;
pq 2=3´0,1´0,9=0,243;
P(X= 2 )=P 3 ( 2 ) =  p2q=3´(0,1)2´(0,9)=0,027; P(X =3 ) = P 3 ( 3 )=p3= 0,13=0,001.
p2q=3´(0,1)2´(0,9)=0,027; P(X =3 ) = P 3 ( 3 )=p3= 0,13=0,001.
Контроль: 0,729+0,243+0,027+0,001=1.
` Закон распределения Х имеет вид:
| хi = k
|
|
|
|
|
| P(X = k)
| 0,729
| 0,243
| 0,027
| 0,001
|
M[X] =  ; D[X]=
; D[X]=  . 3
. 3
Геометрическое гипегеометрическое распределения.
Дискретная СВ Х подчинена геометрическому распределению, если ее возможные значения 0, 1, 2, …, k, …, асоответствующие вероятности можно вычислить по формулам:
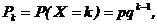
где 0 <p <1, q=1 - р.
| xi
|
|
|
| …
| k
| …
|
| pi
| p
| pq
| pq 2
| …
| pqk
| …
|
Ряд распределения Х имеет вид:
Математическое ожидание и дисперсия соответственно равны:
 D[X]
D[X] 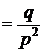 .
.
3. Гипергеометрическое распределения. СВ Хподчинена гипергеометрическому распределению с параметрами a, b, n, если ее возможные значения 0, 1, 2, …, k, …, а, а соответствующие вероятности вычисляются по формулам:
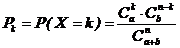 ,
, 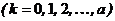 .
.
(Если в урне а белых и b черных шаров и из нее вынимают n шаров, то СВ Х ={число белых шаров среди вынутых} подчиняется гипер-геометрическому закону).
Примечание. В приведенной формуле полагают 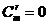 , если
, если 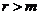 .
.
Математическое ожидание и дисперсия гипергеометричекого распределения: 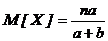 ,
,
D 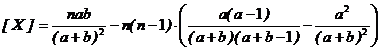 .
.
Распределение Пуассона
СВ Х распределена по закону Пуассона, если онапринимает целые неотрицательные значения: 0, 1, 2, …, k, …, вероятности которых можно вычислить по формулам:
 ,
,
где k – число появлений событияАв n независимыхиспытаниях ( ),
),  (
( )‑ параметр распределения, который равен среднему числу появления события А в n испытаниях. Если вероятность появления события А в каждом испытании одинакова и равна р, то
)‑ параметр распределения, который равен среднему числу появления события А в n испытаниях. Если вероятность появления события А в каждом испытании одинакова и равна р, то 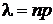 .
.
Распределение Пуассона является предельным для биномиального распределения, когда число испытаний n достаточно велико, а вероятность р появления события в каждом испытании мала (порядка 1/ n).
Ряд распределения СВ Х, распределенной по закону Пуассона, имеет вид:
Математическое ожидание и дисперсия соответственно равны:
 , D
, D  .
.
Пример. На телефонную станцию в течение часа поступают в среднем 30 вызовов. Найти вероятность того, что в течение минуты поступает не более двух вызовов.
4Математическое ожидание числа вызовов за минуту равно  . Вероятность того, что в течение данной минуты будет получено не более двух вызовов, равна сумме вероятностей того, что в течение данной минуты будет либо 0, либо 1, либо 2 вызова. Поэтому искомая вероятность:
. Вероятность того, что в течение данной минуты будет получено не более двух вызовов, равна сумме вероятностей того, что в течение данной минуты будет либо 0, либо 1, либо 2 вызова. Поэтому искомая вероятность:
P (k£2) = p(X=0)+P(X=1)+P(X=2)= =  +
+  +
+  =
=  (1+1/2+
(1+1/2+ 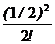 )»0,98. 3
)»0,98. 3
Равномерное распределение
СВ Х подчинена равномерному закону распределения, если ее плотность распределения вероятностей имеет вид:
 .
.
График плотности равномерного распределения f(x) изображен на рис.5.1.
Интегральная функция распределения F (x) равна:  ,
,
ее график изображен на рис. 5.2.
Математическое ожидание, дисперсия и среднее квадратичное отклонение соответственно равны:
 ; D
; D  ;
;  .
.
Вероятность попадания Х в заданный интервал значений  определяется:
определяется:  .
.
Показательное распределение
Непрерывная СВ Х распределена по показательному (экспоненциальному) закону, если ее плотность распределения вероятностей имеет вид:
 ,
,
где l - параметр распределения.
Кривая плотности распределения f (x)изображена на рис.5.3. Интегральная функция распределения равна
 ,
,
ее график показан на рис 5.4.
Математическое ожидание, дисперсия и среднее квадратичное соответственно равны:
M[X]=1/l; D[X]=1/l2; sх=1/l;
а вероятность попадания Х в заданный интервал значений  определяется следующим образом:
определяется следующим образом:  .
.
Пример. СВ Т —время безотказной работы телевизора - имеет показательное распределение. Определить вероятность того, что время безотказной работы телевизора будет не меньше 600 часов, если среднее время работы его 400 часов.
4 По условию задачи математическое ожидание СВ Т равно 400 часов. Искомая вероятность
P(T ³ 600 )= 1- P(T< 600 ) = 1- F (600)=1-(1- e- 600/400 )= e -1,5 » 0,2231. 3
Нормальное распределение
СВ Х подчинена нормальному закону распределения,если ее плотность распределения вероятностей имеет вид:
 ,
,
где a ‑ математическое ожидание,  ‑ среднее квадратичное отклонениеХ.
‑ среднее квадратичное отклонениеХ.
Интегральная функция нормального распределения имеет вид
 ;
;
где  - функция Лапласа, или интеграл вероятностей.
- функция Лапласа, или интеграл вероятностей.
Основные свойства функции Лапласа:
1) F( 0 ) = 0;
2)  (нечетная функция);
(нечетная функция);
3) F (¥)=0,5
Таблица значений функции F(х) для  приведена в приложении, поскольку она является нечетной, то для отрицательных значений х пользуются теми же таблицами, что и для положительных.
приведена в приложении, поскольку она является нечетной, то для отрицательных значений х пользуются теми же таблицами, что и для положительных.
Вероятность попадания Х в заданный интервал значений  :
:
 ,
,
Вероятность того, что абсолютная величина отклонения  нормальной СВ Х от ее математического ожидания меньше положительного числа d, определяется выражением:
нормальной СВ Х от ее математического ожидания меньше положительного числа d, определяется выражением:
 .
.
В частности, при а =0, P(êХ ê<d) =2F(d/s).
Если в равенстве 5.17. 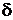 взять
взять  , получим так называемое «правило трёх сигм», которое является одним из необходимых условий того, что СВ имеет нормальный закон распределения. В самом деле,
, получим так называемое «правило трёх сигм», которое является одним из необходимых условий того, что СВ имеет нормальный закон распределения. В самом деле, 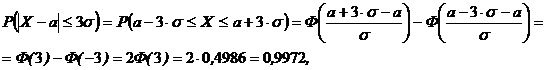
т.е. отклонение нормальной СВ от своего математического ожидания а на величину, равную  является событием практически достоверным.
является событием практически достоверным.
 Асимметрия, эксцесс, мода и медиана нормального распределения соответственно равны:
Асимметрия, эксцесс, мода и медиана нормального распределения соответственно равны:
аs=0, еk=0, Mo=a, Me=a, где a=M[X].
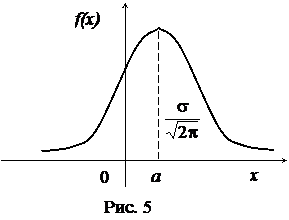
График плотности вероятности нормального распределения (рис.5) называют нормальной кривой (кривой Гаусса).



 , (5.1
, (5.1



 D[X]=npq.
D[X]=npq. pq 2=3´0,1´0,9=0,243;
pq 2=3´0,1´0,9=0,243; p2q=3´(0,1)2´(0,9)=0,027; P(X =3 ) = P 3 ( 3 )=p3= 0,13=0,001.
p2q=3´(0,1)2´(0,9)=0,027; P(X =3 ) = P 3 ( 3 )=p3= 0,13=0,001. ; D[X]=
; D[X]=  . 3
. 3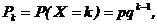
 D[X]
D[X] 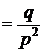 .
.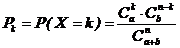 ,
, 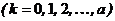 .
.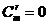 , если
, если 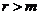 .
.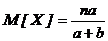 ,
,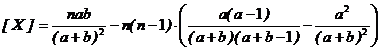 .
. ,
, ),
),  (
( )‑ параметр распределения, который равен среднему числу появления события А в n испытаниях. Если вероятность появления события А в каждом испытании одинакова и равна р, то
)‑ параметр распределения, который равен среднему числу появления события А в n испытаниях. Если вероятность появления события А в каждом испытании одинакова и равна р, то 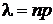 .
.
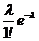


 , D
, D  .
. . Вероятность того, что в течение данной минуты будет получено не более двух вызовов, равна сумме вероятностей того, что в течение данной минуты будет либо 0, либо 1, либо 2 вызова. Поэтому искомая вероятность:
. Вероятность того, что в течение данной минуты будет получено не более двух вызовов, равна сумме вероятностей того, что в течение данной минуты будет либо 0, либо 1, либо 2 вызова. Поэтому искомая вероятность: +
+  +
+  (1+1/2+
(1+1/2+ 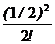 )»0,98. 3
)»0,98. 3 .
. ,
,
 ; D
; D  ;
;  .
. определяется:
определяется:  .
. ,
, ,
,
 .
. ,
, ‑ среднее квадратичное отклонениеХ.
‑ среднее квадратичное отклонениеХ. ;
; - функция Лапласа, или интеграл вероятностей.
- функция Лапласа, или интеграл вероятностей. (нечетная функция);
(нечетная функция); приведена в приложении, поскольку она является нечетной, то для отрицательных значений х пользуются теми же таблицами, что и для положительных.
приведена в приложении, поскольку она является нечетной, то для отрицательных значений х пользуются теми же таблицами, что и для положительных. :
: ,
, нормальной СВ Х от ее математического ожидания меньше положительного числа d, определяется выражением:
нормальной СВ Х от ее математического ожидания меньше положительного числа d, определяется выражением: .
.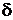 взять
взять  , получим так называемое «правило трёх сигм», которое является одним из необходимых условий того, что СВ имеет нормальный закон распределения. В самом деле,
, получим так называемое «правило трёх сигм», которое является одним из необходимых условий того, что СВ имеет нормальный закон распределения. В самом деле, 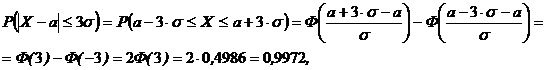
 является событием практически достоверным.
является событием практически достоверным. Асимметрия, эксцесс, мода и медиана нормального распределения соответственно равны:
Асимметрия, эксцесс, мода и медиана нормального распределения соответственно равны:


