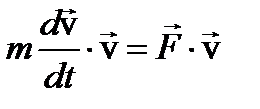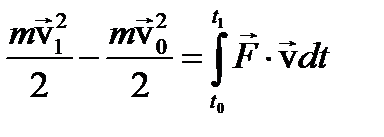Векторный способ
 Пусть точка М движется относительно системы отсчета Oxyz
Пусть точка М движется относительно системы отсчета Oxyz
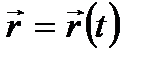 С течением времени положение точки М относительно данной системы отсчета меняется
С течением времени положение точки М относительно данной системы отсчета меняется
Координатный способ 
Камера Вильсона. Визуализация траекторий элементарных частиц

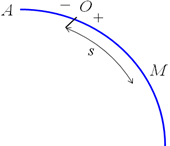 Пусть точка М движется вдоль траектории АВ. Выберем на этой траектории какую-нибудь точку О, которую примем за начало отсчета. Будем считать траекторию криволинейной координатной осью и установим на ней положительное и отрицательное направления. Введем криволинейную координату s, длину криволинейного отрезка ОМ, взятую с соответствующим знаком. Закон движения точки вдоль траектории s=s(t)
Пусть точка М движется вдоль траектории АВ. Выберем на этой траектории какую-нибудь точку О, которую примем за начало отсчета. Будем считать траекторию криволинейной координатной осью и установим на ней положительное и отрицательное направления. Введем криволинейную координату s, длину криволинейного отрезка ОМ, взятую с соответствующим знаком. Закон движения точки вдоль траектории s=s(t)
 Стоит заметить, что уравнение s = s (t) определяет положение точки на траектории, а не путь, пройденный ею. Пройденный путь равен
Стоит заметить, что уравнение s = s (t) определяет положение точки на траектории, а не путь, пройденный ею. Пройденный путь равен
Скорость

Рассмотрим движение точки М вдоль траектории. Пройденный путь равен D s ~ D r. Введем среднюю скорость 
Переходя здесь к пределу D t → 0, получим мгновенную скорость точки 
С корость материальной точки – это векторная кинематическая характеристика точки, определяющая быстроту изменения ее положения относительно данной системы координат и равная производной от радиус-вектора точки по времени. Вектор скорости точки направлен по касательной к траектории в сторону ее движения.
Ускорение


 Как определить быстроту изменения скорости точки? Пусть материальная точка М движется вдоль траектории. Определим приращение скорости за время D t. Определим среднее ускорение
Как определить быстроту изменения скорости точки? Пусть материальная точка М движется вдоль траектории. Определим приращение скорости за время D t. Определим среднее ускорение 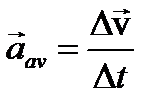 Переходя здесь к пределу D t → 0, получим мгновенное ускорение точки
Переходя здесь к пределу D t → 0, получим мгновенное ускорение точки
Таким образом, ускорение точки – это векторная кинематическая величина, характеризующая быстроту изменения ее скорости и равная первой производной от скорости или второй производной от радиус-вектора по времени

тангенциальное ускорение, характеризующее изменение скорости по величине
нормальное ускорение, характеризующее изменение скорости по направлению

Задание движения ТТ.
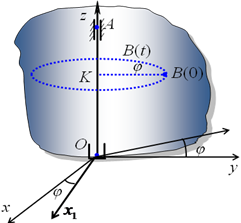
Пусть дано твердое тело (ТТ) По определению это совокупность материальных точек, расстояние между
которыми фиксированы и не меняются со временем
Закон движения скольки точек нужно задать, чтобы определить движение ТТ?
Пусть задан закон движения 
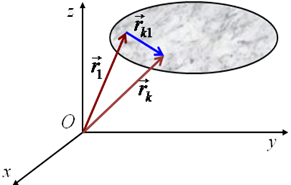
Радиус-вектор произвольной точки k твердого тела равен

Модуль вектора постоянен, но относительная скорость 
Таким образом, знание кинематических характеристик одной точки твердого тела не позволяет определить кинематические характеристики любой другой его точки
 Степени свободы
Степени свободы
Положение трех точек твердого тела в произвольный момент времени характеризуется девятью координатами

Поскольку, однако, в твердом теле расстояния между любыми двумя его точками постоянны, то эти координаты связаны тремя условиями

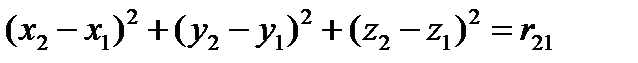

Число независимых параметров (или координат),
определяющих положение системы в пространстве,
называется числом степеней свободы
 Поступательным называется такое движение тела, при котором прямая, соединяющая две любые точки тела, остается в процессе движения параллельной самой себе. Очевидно, любое прямолинейное движение твердого тела является поступательным. Однако есть примеры поступательных движений, когда траектории отдельных его точек вовсе не являются прямыми линиями. Cпарник АВ при вращении кривошипов АС и BD также движется поступательно, он остается параллельным самому себе.
Поступательным называется такое движение тела, при котором прямая, соединяющая две любые точки тела, остается в процессе движения параллельной самой себе. Очевидно, любое прямолинейное движение твердого тела является поступательным. Однако есть примеры поступательных движений, когда траектории отдельных его точек вовсе не являются прямыми линиями. Cпарник АВ при вращении кривошипов АС и BD также движется поступательно, он остается параллельным самому себе.
 При поступательном движении твердого тела все его точки
При поступательном движении твердого тела все его точки
описывают конгруэнтные траектории и имеют в каждый
момент времени одинаковые скорости и ускорения
 Для любых двух точек А и В
Для любых двух точек А и В




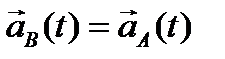
Таким образом, траектория точки В получается из траектории точки А простым сдвигом на постоянный вектор, это и означает, что траектории конгруэнтны (при наложении совпадают)
Угловая скорость

 За промежуток времени D t тело повернется на угол D φ
За промежуток времени D t тело повернется на угол D φ
Переходя к пределу, получим мгновенную
 угловую скорость
угловую скорость
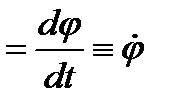
 Угловая скорость измеряется в радианах в секунду или числом оборотов в минуту
Угловая скорость измеряется в радианах в секунду или числом оборотов в минуту
Вектор угловой скорости ω направлен вдоль оси вращения в сторону, откуда это вращение видно происходящим против часовой стрелки 
 Угловое ускорение. Если за промежуток времени D t угловая скорость тела изменяется на D ω, то можно ввести среднее угловое ускорение тела за время D t
Угловое ускорение. Если за промежуток времени D t угловая скорость тела изменяется на D ω, то можно ввести среднее угловое ускорение тела за время D t

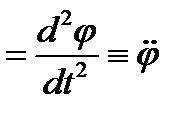 Переходя к пределу, получим мгновенное угловое ускорение
Переходя к пределу, получим мгновенное угловое ускорение



:
Передаточные механизмы

 Вал I вращается с угловой скоростью ω 1. Определить угловую скорость вращения вала II, если радиусы колес (шестерней) механизма равны r 1, r 2, r 3, r 4. Колесо 1 жестко скреплено с валом I, поэтому
Вал I вращается с угловой скоростью ω 1. Определить угловую скорость вращения вала II, если радиусы колес (шестерней) механизма равны r 1, r 2, r 3, r 4. Колесо 1 жестко скреплено с валом I, поэтому
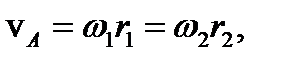
 w I = w 1 Аналогично w 4 = w II Приравнивая скорости в точках A и B контакта колес, получим
w I = w 1 Аналогично w 4 = w II Приравнивая скорости в точках A и B контакта колес, получим
Учитывая, что колеса 2 и 3 жестко скреплены, получаем


Движение твердого тела называется плоским (плоскопараллельным), если все точки тела движутся в плоскостях, параллельных некоторой неподвижной плоскости 
Иллюстрация работы кривошипно-шатунного механизма. Передача движения колесу
 Уравнение плоского движения
Уравнение плоского движения
Будем описывать движение сечения S
относительно неподвижной системы координат
Oxy, жестко связанной с плоскостью P
 Положение сечения относительно этой системы координат определяется положением какого- либо принадлежащего ему отрезка AB
Положение сечения относительно этой системы координат определяется положением какого- либо принадлежащего ему отрезка AB
Т.о., плоское движение ТТ слагается из поступательного
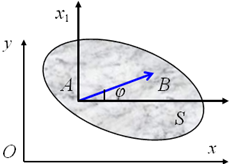 движения вместе с полюсом и вращения вокруг полюса
движения вместе с полюсом и вращения вокруг полюса
Этим степеням свободы соответствует движение вдоль осей Оу и Ох и вращение относительно
некоторой точки
Введем вспомогательную систему координат с
началом в точке А (полюсе) тела и осями параллельными соответствующим осям неподвижной системы координат
Теорема о МЦС
Мгновенным центром скоростей (МЦС) сечения тела (или плоской фигуры) называется точка, скорость которой в данный момент времени равна нулю
Теорема: Если угловая скорость рассматриваемого сечения S в данный момент времени отлична от нуля, то мгновенный центр скоростей существует и единственен
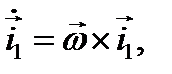

 Действительно, рассмотрим сечение S
Действительно, рассмотрим сечение S

 Пусть в некоторый момент времени t точки A и B
Пусть в некоторый момент времени t точки A и B
имеют скорости, не параллельные друг другу

 Это следует из теоремы о проекциях скоростей, так
Это следует из теоремы о проекциях скоростей, так
 как если бы скорость была отлична от нуля, то
как если бы скорость была отлична от нуля, то
она одновременно должна была бы быть перпендикулярна к АА’ и BB’. Последнее, однако,не возможно в силу непараллельности скоростей точек А и В
Теорема Кориолиса

Если точка покоится относительно подвижной системы отсчета, то ее движение совпадает с переносным движением, а абсолютное ускорение – с переносным ускорением
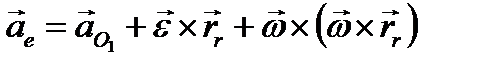
Теорема. Абсолютное ускорение точки равно сумме
относительного, переносного и кориолисова ускорений
Ускорение Кориолиса
Это ускорение обращается в нуль, если угловая скорость подвижной системы отсчета равна нулю ω= 0, т. е. переносное движение поступательное
угловая скорость вращения подвижной системы отсчета параллельна
относительной скорости ω относительная скорость точки равна нулю
 Модуль ускорения Кориолиса равен
Модуль ускорения Кориолиса равен
Задачи динамики
Механической системой называется совокупность взаимодействующих между собой материальных точек или тел.
Динамика изучает движение данных точек или тел, возникающее при их взаимодействии
Задачи динамики
Первая задача состоит в определении сил, действующих на механическую систему, по заданному закону ее движения
Во второй же заданы силы, действующие на механическую систему и необходимо найти закон ее движения
На практике часто приходится решать смешанную задачу, когда часть сил известна, а некоторые (реакции связей) необходимо найти наряду с законом движения
Закон инерции Галилея
 Свободная материальная точка покоится или равномерно и прямолинейно двигается
Свободная материальная точка покоится или равномерно и прямолинейно двигается
Сформулированная аксиома является выражением того экспериментального факта, что отличить состояние покоя от равномерного и прямолинейного движения нельзя
 Действительно, если относительно некоторой системы отсчета К точка покоится, то всегда можно построить такую систему К ’, относительно которой данная точка будет двигаться равномерно и прямолинейно
Действительно, если относительно некоторой системы отсчета К точка покоится, то всегда можно построить такую систему К ’, относительно которой данная точка будет двигаться равномерно и прямолинейно



 Т.о., точка М в движется относительно системы К’ прямолинейно со скоростью
Т.о., точка М в движется относительно системы К’ прямолинейно со скоростью
 Второй закон Ньютона
Второй закон Ньютона

 аксиома 2 Если в некоторой инерциальной системе отсчета на свободную материальную точку действует сила, то скорость изменения импульса (количества движения) материальной точки равна действующей на нее силе
аксиома 2 Если в некоторой инерциальной системе отсчета на свободную материальную точку действует сила, то скорость изменения импульса (количества движения) материальной точки равна действующей на нее силе
 Т.о., масса является мерой инерции тела. Инертность тела, т.е. его способность двигаться без изменения скорости тем больше, чем больше масса. По этой причине эту массу называют инертной
Т.о., масса является мерой инерции тела. Инертность тела, т.е. его способность двигаться без изменения скорости тем больше, чем больше масса. По этой причине эту массу называют инертной
 Масса величина аддитивная и скалярная
Масса величина аддитивная и скалярная
В классической механике предполагается, что масса тела во всех инерциальных системах отсчета одинакова и не меняется со временем


Третий закон Ньютона
Две материальные точки действуют друг на друга с
силами, равными по величине и направленными вдоль

 одной прямой в противоположные стороны
одной прямой в противоположные стороны



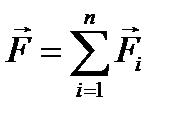
 Аксиома 4 Действие на материальную точку произвольной системы n сил эквивалентно действию одной силы, равной их сумме
Аксиома 4 Действие на материальную точку произвольной системы n сил эквивалентно действию одной силы, равной их сумме
Аксиома связей Всякое несвободное тело можно рассматривать как свободное, если отбросить связи и заменить их реакциями 
Закон инерции Галилея постулирует существование инерциальных систем отсчета, и тем самым указывает на рамки применимости второго закона Ньютона. Сформулированные аксиомы применимы лишь в инерциальных системах отсчета
Основная задача динамики
Решение второй задачи динамики сводится к решению системы трех дифференциальных уравнений второго порядка


Эти три уравнения эквивалентны системе шести дифференциальных уравнений первого порядка
 Общее решение этой системы уравнений зависит от шести произвольных постоянных и имеет вид
Общее решение этой системы уравнений зависит от шести произвольных постоянных и имеет вид
Изменяя в общем решении постоянные интегрирования, мы будем получать различные решения
Каждое из этих решений будет описывать некоторое движение материальной точки под действием одной и тоже силы
Начальные условия
Характер этих движений может быть разным и определяется начальными условиями, т.е. координатой и скоростью материальной точки в начальный момент времени t = 0


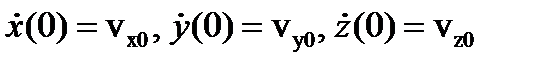 В результате каждая из постоянных Ci может быть вычислена, как функция начальных данных.
В результате каждая из постоянных Ci может быть вычислена, как функция начальных данных.

Подставляя эти постоянные в общее решение, получим искомое частное решение задачи, соответствующее конкретным начальным условиям

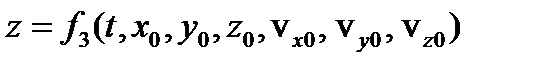
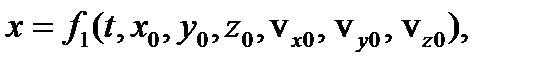


Сложность решения основной задачи динамики состоит в том, что сила в общем случае может зависеть не только от времени, но и от координат точки и ее скоростей
Поэтому в общем случае системы уравнений Ньютона – это системы нелинейных дифференциальных уравнений
 ДУ с разделяющимися переменными
ДУ с разделяющимися переменными
Обыкновенным ДУ с разделяющимися переменными называют уравнение вида

Общее решение такого уравнения имеет вид

 Чтобы решить задачу Коши, необходимо определить постоянную С по НУ
Чтобы решить задачу Коши, необходимо определить постоянную С по НУ

Решение задачи Коши
При прямолинейном движении точки ее скорость направлена вдоль линии действия силы

 ДУ прямолинейного движения точки имеет вид
ДУ прямолинейного движения точки имеет вид
Это уравнение эквивалентно системе двух ДУ первого порядка

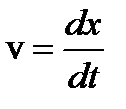
 Задача Коши решается последовательным их интегрированием
Задача Коши решается последовательным их интегрированием

где постоянные определяются из НУ:

Криволинейное движение



Сила сопротивления
 Выберем начало координат в положении статического равновесия пружины
Выберем начало координат в положении статического равновесия пружины
Второй закон Ньютона

 ДУ свободных затухающих колебаний
ДУ свободных затухающих колебаний

Характеристическое уравнение данного ДУ

В зависимости от соотношения b и ω возможны три различных случая движения точки с массой m
Апериодическое движение



Случай большого сопротивления, b > ω, оба решения
Уравнение движения

Это неоднородное уравнение и его решение имеет вид

 х 1 – общее решение однородного уравнения
х 1 – общее решение однородного уравнения
х 2 частное решение неоднородного уравнения ищем в виде
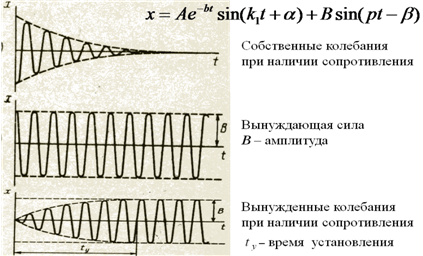

Коэффициент динамичности
Уравнения Ньютона в НСО

Невесомость
Условие невесомости

 Силы инерции равна
Силы инерции равна


 Пусть сила тяжести
Пусть сила тяжести
Классификация сил

Силовое поле действует на каждую материальную точку системы
Силы, которые действуют между точками механической системы, называются внутренними
Силы, с которыми на точки системы действуют окружающие ее тела или поля, называются внешними
Свойства внутренних сил
По третьему закону Ньютона силы, с которыми взаимодействуют две точки равны по величине и противоположно направлены


 Главный вектор всех внутренних сил равен нулю
Главный вектор всех внутренних сил равен нулю

Главный момент всех внутренних сил относительно произвольной
 точки равен нулю
точки равен нулю
Центр масс
 Важнейшей динамической характеристикой материальной точки, определяющей ее способность сохранять движение, является масса
Важнейшей динамической характеристикой материальной точки, определяющей ее способность сохранять движение, является масса
Так как механическая система состоит из N материальных
 точек с массой mi, то можно ввести массу всей системы, равную сумме масс ее точек
точек с массой mi, то можно ввести массу всей системы, равную сумме масс ее точек
Центром масс механической системы или центром инерции относительно некоторой декартовой системы координат называется точка с координатами

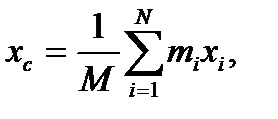

 Координаты ЦМ твердого тела
Координаты ЦМ твердого тела
 Если плотность распределения массы равна, то
Если плотность распределения массы равна, то


 Координаты центра масс равны
Координаты центра масс равны



Переходя к пределу, имеем


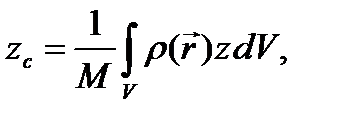

Радиус инерции
Если момент инерции системы относительно оси Ox равен Jx, а ее масса – М, то величина
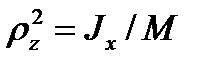
называется радиусом инерции системы относительно оси Oх Радиус инерции определяет расстояние от оси Oх до точки,
в которой нужно сосредоточить всю массу тела (системы),
чтобы момент инерции этой точки был равен моменту
 инерции всего тела (системы)
инерции всего тела (системы)
 Теорема Гюйгенса
Теорема Гюйгенса
Если ось Oz проходит через центр масс системы, то

Момент инерции системы относительно данной оси равен моменту инерции относительно оси, ей параллельной и проходящей через центр масс тела, плюс произведение его массы системы на квадрат расстояния между осями
Система уравнений движения

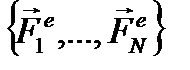 Пусть дана механическая система, состоящая из N взаимодействующих точек,на которую действуют внешние силы
Пусть дана механическая система, состоящая из N взаимодействующих точек,на которую действуют внешние силы
 Равнодействующую всех внутренних сил, действующих на k- ю точку со стороны других точек, обозначим так:
Равнодействующую всех внутренних сил, действующих на k- ю точку со стороны других точек, обозначим так:
 Тогда для каждой k- ойточки системы в инерциальной системе координат Oxyz уравнение движение имеет вид
Тогда для каждой k- ойточки системы в инерциальной системе координат Oxyz уравнение движение имеет вид


где - силы реакций связей, наложенных на k -ю точку
Число этих уравнений равно N, а общее решение зависит в общем случае от 6 N произвольных скалярных постоянных
Теорема о движении ЦМ

 Уравнения движения системы имеют вид
Уравнения движения системы имеют вид
 Чтобы найти закон движения ЦМ системы, просуммируем эти уравнения
Чтобы найти закон движения ЦМ системы, просуммируем эти уравнения

Теорема о движении ЦМ


 Центр масс системы движется как материальная точка, масса которой равна массе всей системы и к которой приложены все внешние силы, действующие на систему
Центр масс системы движется как материальная точка, масса которой равна массе всей системы и к которой приложены все внешние силы, действующие на систему
Теорема о движении ЦМС
Если сумма внешних сил действующих на систему равна нулю, то ее ЦМ движется равномерно и прямолинейно.
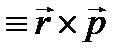
 Если в начальный момент времени ЦМ покоился, то он останется в покое и в дальнейшем. Если сумма проекций внешних сил на какую-нибудь ось (например ось x) равна нулю, то вдоль этой оси ЦМС движется равномерно и прямолинейно или покоится, если он покоился в начальный момент времени
Если в начальный момент времени ЦМ покоился, то он останется в покое и в дальнейшем. Если сумма проекций внешних сил на какую-нибудь ось (например ось x) равна нулю, то вдоль этой оси ЦМС движется равномерно и прямолинейно или покоится, если он покоился в начальный момент времени
Закон сохранения импульса
 Важнейшим следствие данной теоремы является закон сохранения импульса
Важнейшим следствие данной теоремы является закон сохранения импульса
 Если главный вектор внешних сил, действующих на систему, равен нулю, то ее импульс сохраняется
Если главный вектор внешних сил, действующих на систему, равен нулю, то ее импульс сохраняется
g LqyuuVRwOe+nKQjnkTU2lknBjRxsNw+jNWbaXvmd+pMvRYCwy1BB5X2bSemKigy6mW2Jg/dpO4M+ yK6UusNrgJtGxlG0kAZrDgsVtrSrqPg+/RgFi8PrV5q+RXOXT/qVj/NDge2HUuPH4eUZhKfB38P/ 7aNWkCxX8VMCf3/CF5CbXwAAAP//AwBQSwECLQAUAAYACAAAACEA2+H2y+4AAACFAQAAEwAAAAAA AAAAAAAAAAAAAAAAW0NvbnRlbnRfVHlwZXNdLnhtbFBLAQItABQABgAIAAAAIQBa9CxbvwAAABUB AAALAAAAAAAAAAAAAAAAAB8BAABfcmVscy8ucmVsc1BLAQItABQABgAIAAAAIQD8NVHeyAAAAN8A AAAPAAAAAAAAAAAAAAAAAAcCAABkcnMvZG93bnJldi54bWxQSwUGAAAAAAMAAwC3AAAA/AIAAAAA " fillcolor="blue"> 

 Если проекция главного вектора внешних сил, действующих на систему, на некоторую ось равна нулю, то проекция импульса системы на эту ось также сохраняется
Если проекция главного вектора внешних сил, действующих на систему, на некоторую ось равна нулю, то проекция импульса системы на эту ось также сохраняется

Импульс силы
Для характеристики действия, оказываемого на тело силой за некоторый промежуток времени, вводится понятие импульса силы
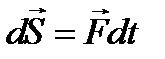 Элементарным импульсом силы называется вектор, равный произведению силы на элементарный промежуток времени
Элементарным импульсом силы называется вектор, равный произведению силы на элементарный промежуток времени
 Импульсом силы за конечный промежуток времени
Импульсом силы за конечный промежуток времени
называется вектор

Интегральная форма теоремы
Дифференциальная форма теоремы об изменении импульса
 с помощью понятия импульса силы может быть представлена в интегральном виде
с помощью понятия импульса силы может быть представлена в интегральном виде


 Изменение импульса механической системы за некоторый промежуток времени равно главному вектору импульсов всех внешних сил, действующих на систему в этот промежуток времени
Изменение импульса механической системы за некоторый промежуток времени равно главному вектору импульсов всех внешних сил, действующих на систему в этот промежуток времени
Особенно простой вид эта теорема имеет для точки
Внутренние силы непосредственно не могут влиять
на изменение импульса системы
Момент импульса
Моментом импульса (моментом количества движения) точки относительно некоторого центра О называется вектор, равный векторному произведению ее радиус-вектора относительно этой точки на ее импульс




Теорема II
Производная по времени от момента импульса материальной точки относительно осиравна моменту приложенной к точке силы относительно той же оси
 Теорема сохранения момента импульса точки
Теорема сохранения момента импульса точки
Пусть


Теорема III
 Если при движении точки момент действующей на нее
Если при движении точки момент действующей на нее
силы относительно центра О равен нулю, то ее момент
 импульса сохраняется
импульса сохраняется
Теорема I
Производная по времени от главного момента импульса системы относительно центра О равна главному моменту внешних сил, приложенных к этой системе, относительно
 того же центра
того же центра
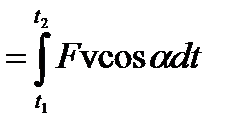




Д-во:
Для k-ой материальной точки
Просуммируем эти уравнения по всем точкам системы
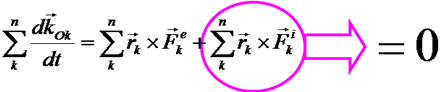
Теорема II
Производная по времени от проекции главного момента импульса системы относительно осиравна главному моменту внешних сил, приложенных к этой системе, относительно той же оси

Элементарная работа силы
Пусть точка под действием силы F движется вдоль траектории LL’
За время dt материальная точка под действием этой силы смещается на величину элементарного перемещения dr


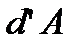
Элементарной работой силы на перемещении называется скалярное произведение

Потенциальные силы
Силовое поле называется потенциальным в том случае,
если существует скалярная функция U, зависящая только


 от координат материальной точки, такая, что
от координат материальной точки, такая, что
Функция U называется потенциалом или потенциальной
энергией
Из определения потенциальной энергии следует, что она
определена с точностью до некоторой постоянной С.
Потенциалы U и U+C дают одинаковую силу. Поэтому физический смысл имеет только разность потенциалов
 Вектор потенциальной силы определяется выражением
Вектор потенциальной силы определяется выражением
Кинетическая энергия
 Кинетическая энергия материальной точки i, равна половине произведения массы точки на квадрат ее скорости
Кинетическая энергия материальной точки i, равна половине произведения массы точки на квадрат ее скорости
 Кинетическая энергия аддитивна, поэтому кинетическая энергия системы n материальных точек определяется суммой
Кинетическая энергия аддитивна, поэтому кинетическая энергия системы n материальных точек определяется суммой

Теорема Кенига
 Кинетическая энергия материальной точки i, складывается из кинетической энергии ее центра масс, в котором сосредоточена вся масса системы, и кинетической энергии движения системы относительно центра масс
Кинетическая энергия материальной точки i, складывается из кинетической энергии ее центра масс, в котором сосредоточена вся масса системы, и кинетической энергии движения системы относительно центра масс
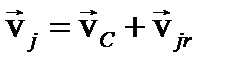 Д-во: Скорость любой точки i можно представить, как движение вместе c центром масс и относительно центра масс
Д-во: Скорость любой точки i можно представить, как движение вместе c центром масс и относительно центра масс


 Теорема об изменении кинетической энергии точки
Теорема об изменении кинетической энергии точки
Работа силы характеризует то, насколько эффективно точка перемещается под действием этой силы
 Остается, однако, не ясной связь между работой силы, приложенной к точке, и изменением ее скорости
Остается, однако, не ясной связь между работой силы, приложенной к точке, и изменением ее скорости
Установим эту связь
Умножим это уравнение скалярно на скорость точки
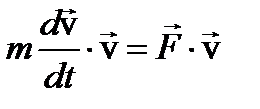


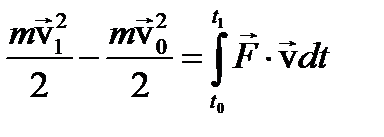
Проинтегрируем это уравнение
Теорема I
Изменение кинетической энергии движущейся материальной точки равно работе приложенной к ней силе на пройденном точкой пути
Векторный способ
 Пусть точка М движется относительно системы отсчета Oxyz
Пусть точка М движется относительно системы отсчета Oxyz
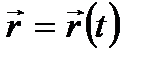 С течением времени положение точки М относительно данной системы отсчета меняется
С течением времени положение точки М относительно данной системы отсчета меняется
Координатный способ 
Камера Вильсона. Визуализация траекторий элементарных частиц

 Пусть точка М движется вдоль траектории АВ. Выберем на этой траектории какую-нибудь точку О, которую примем за начало отсчета. Будем считать траекторию криволинейной координатной осью и установим на ней положительное и отрицательное направления. Введем криволинейную координату s, длину криволинейного отрезка ОМ, взятую с соответствующим знаком. Закон движения точки вдоль траектории s=s(t)
Пусть точка М движется вдоль траектории АВ. Выберем на этой траектории какую-нибудь точку О, которую примем за начало отсчета. Будем считать траекторию криволинейной координатной осью и установим на ней положительное и отрицательное направления. Введем криволинейную координату s, длину криволинейного отрезка ОМ, взятую с соответствующим знаком. Закон движения точки вдоль траектории s=s(t)
 Стоит заметить, что уравнение s = s (t) определяет положение точки на траектории, а не путь, пройденный ею. Пройденный путь равен
Стоит заметить, что уравнение s = s (t) определяет положение точки на траектории, а не путь, пройденный ею. Пройденный путь равен
Скорость

Рассмотрим движение точки М вдоль траектории. Пройденный путь равен D s ~ D r. Введем среднюю скорость 
Переходя здесь к пределу D t → 0, получим мгновенную скорость точки 
С корость материальной точки – это векторная кинематическая характеристика точки, определяющая быстроту изменения ее положения относительно данной системы координат и равная производной от радиус-вектора точки по времени. Вектор скорости точки направлен по касательной к траектории в сторону ее движения.
Ускорение


 Как определить быстроту изменения скорости точки? Пусть материальная точка М движется вдоль траектории. Определим приращение скорости за время D t. Определим среднее ускорение
Как определить быстроту изменения скорости точки? Пусть материальная точка М движется вдоль траектории. Определим приращение скорости за время D t. Определим среднее ускорение 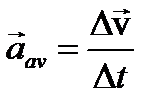 Переходя здесь к пределу D t → 0, получим мгновенное ускорение точки
Переходя здесь к пределу D t → 0, получим мгновенное ускорение точки
Таким образом, ускорение точки – это векторная кинематическая величина, характеризующая быстроту изменения ее скорости и равная первой производной от скорости или второй производной от радиус-вектора по времени

тангенциальное ускорение, характеризующее изменение скорости по величине
нормальное ускорение, характеризующее изменение скорости по направлению

Задание движения ТТ.


Пусть дано твердое тело (ТТ) По определению это совокупность материальных точек, расстояние между
которыми фиксированы и не меняются со временем
Закон движения скольки точек нужно задать, чтобы определить движение ТТ?
|
|
|



 Пусть точка М движется относительно системы отсчета Oxyz
Пусть точка М движется относительно системы отсчета Oxyz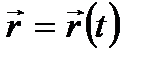 С течением времени положение точки М относительно данной системы отсчета меняется
С течением времени положение точки М относительно данной системы отсчета меняется

 Пусть точка М движется вдоль траектории АВ. Выберем на этой траектории какую-нибудь точку О, которую примем за начало отсчета. Будем считать траекторию криволинейной координатной осью и установим на ней положительное и отрицательное направления. Введем криволинейную координату s, длину криволинейного отрезка ОМ, взятую с соответствующим знаком. Закон движения точки вдоль траектории s=s(t)
Пусть точка М движется вдоль траектории АВ. Выберем на этой траектории какую-нибудь точку О, которую примем за начало отсчета. Будем считать траекторию криволинейной координатной осью и установим на ней положительное и отрицательное направления. Введем криволинейную координату s, длину криволинейного отрезка ОМ, взятую с соответствующим знаком. Закон движения точки вдоль траектории s=s(t) Стоит заметить, что уравнение s = s (t) определяет положение точки на траектории, а не путь, пройденный ею. Пройденный путь равен
Стоит заметить, что уравнение s = s (t) определяет положение точки на траектории, а не путь, пройденный ею. Пройденный путь равен




 Как определить быстроту изменения скорости точки? Пусть материальная точка М движется вдоль траектории. Определим приращение скорости за время D t. Определим среднее ускорение
Как определить быстроту изменения скорости точки? Пусть материальная точка М движется вдоль траектории. Определим приращение скорости за время D t. Определим среднее ускорение 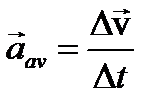 Переходя здесь к пределу D t → 0, получим мгновенное ускорение точки
Переходя здесь к пределу D t → 0, получим мгновенное ускорение точки






 Степени свободы
Степени свободы

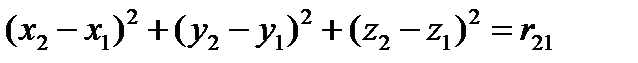

 Поступательным называется такое движение тела, при котором прямая, соединяющая две любые точки тела, остается в процессе движения параллельной самой себе. Очевидно, любое прямолинейное движение твердого тела является поступательным. Однако есть примеры поступательных движений, когда траектории отдельных его точек вовсе не являются прямыми линиями. Cпарник АВ при вращении кривошипов АС и BD также движется поступательно, он остается параллельным самому себе.
Поступательным называется такое движение тела, при котором прямая, соединяющая две любые точки тела, остается в процессе движения параллельной самой себе. Очевидно, любое прямолинейное движение твердого тела является поступательным. Однако есть примеры поступательных движений, когда траектории отдельных его точек вовсе не являются прямыми линиями. Cпарник АВ при вращении кривошипов АС и BD также движется поступательно, он остается параллельным самому себе. При поступательном движении твердого тела все его точки
При поступательном движении твердого тела все его точки Для любых двух точек А и В
Для любых двух точек А и В



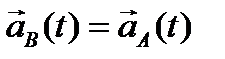

 За промежуток времени D t тело повернется на угол D φ
За промежуток времени D t тело повернется на угол D φ угловую скорость
угловую скорость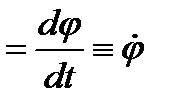
 Угловая скорость измеряется в радианах в секунду или числом оборотов в минуту
Угловая скорость измеряется в радианах в секунду или числом оборотов в минуту
 Угловое ускорение. Если за промежуток времени D t угловая скорость тела изменяется на D ω, то можно ввести среднее угловое ускорение тела за время D t
Угловое ускорение. Если за промежуток времени D t угловая скорость тела изменяется на D ω, то можно ввести среднее угловое ускорение тела за время D t
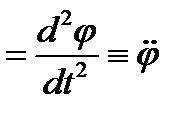 Переходя к пределу, получим мгновенное угловое ускорение
Переходя к пределу, получим мгновенное угловое ускорение



 Вал I вращается с угловой скоростью ω 1. Определить угловую скорость вращения вала II, если радиусы колес (шестерней) механизма равны r 1, r 2, r 3, r 4. Колесо 1 жестко скреплено с валом I, поэтому
Вал I вращается с угловой скоростью ω 1. Определить угловую скорость вращения вала II, если радиусы колес (шестерней) механизма равны r 1, r 2, r 3, r 4. Колесо 1 жестко скреплено с валом I, поэтому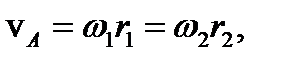
 w I = w 1 Аналогично w 4 = w II Приравнивая скорости в точках A и B контакта колес, получим
w I = w 1 Аналогично w 4 = w II Приравнивая скорости в точках A и B контакта колес, получим


 Уравнение плоского движения
Уравнение плоского движения Положение сечения относительно этой системы координат определяется положением какого- либо принадлежащего ему отрезка AB
Положение сечения относительно этой системы координат определяется положением какого- либо принадлежащего ему отрезка AB движения вместе с полюсом и вращения вокруг полюса
движения вместе с полюсом и вращения вокруг полюса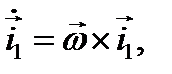

 Действительно, рассмотрим сечение S
Действительно, рассмотрим сечение S
 Пусть в некоторый момент времени t точки A и B
Пусть в некоторый момент времени t точки A и B
 Это следует из теоремы о проекциях скоростей, так
Это следует из теоремы о проекциях скоростей, так как если бы скорость была отлична от нуля, то
как если бы скорость была отлична от нуля, то
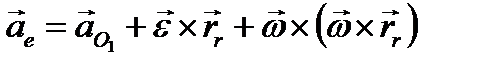
 Модуль ускорения Кориолиса равен
Модуль ускорения Кориолиса равен Свободная материальная точка покоится или равномерно и прямолинейно двигается
Свободная материальная точка покоится или равномерно и прямолинейно двигается Действительно, если относительно некоторой системы отсчета К точка покоится, то всегда можно построить такую систему К ’, относительно которой данная точка будет двигаться равномерно и прямолинейно
Действительно, если относительно некоторой системы отсчета К точка покоится, то всегда можно построить такую систему К ’, относительно которой данная точка будет двигаться равномерно и прямолинейно


 Т.о., точка М в движется относительно системы К’ прямолинейно со скоростью
Т.о., точка М в движется относительно системы К’ прямолинейно со скоростью Второй закон Ньютона
Второй закон Ньютона
 аксиома 2 Если в некоторой инерциальной системе отсчета на свободную материальную точку действует сила, то скорость изменения импульса (количества движения) материальной точки равна действующей на нее силе
аксиома 2 Если в некоторой инерциальной системе отсчета на свободную материальную точку действует сила, то скорость изменения импульса (количества движения) материальной точки равна действующей на нее силе Т.о., масса является мерой инерции тела. Инертность тела, т.е. его способность двигаться без изменения скорости тем больше, чем больше масса. По этой причине эту массу называют инертной
Т.о., масса является мерой инерции тела. Инертность тела, т.е. его способность двигаться без изменения скорости тем больше, чем больше масса. По этой причине эту массу называют инертной


 одной прямой в противоположные стороны
одной прямой в противоположные стороны


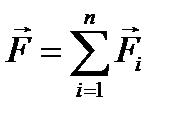
 Аксиома 4 Действие на материальную точку произвольной системы n сил эквивалентно действию одной силы, равной их сумме
Аксиома 4 Действие на материальную точку произвольной системы n сил эквивалентно действию одной силы, равной их сумме

 Общее решение этой системы уравнений зависит от шести произвольных постоянных и имеет вид
Общее решение этой системы уравнений зависит от шести произвольных постоянных и имеет вид

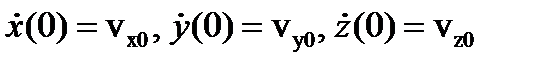 В результате каждая из постоянных Ci может быть вычислена, как функция начальных данных.
В результате каждая из постоянных Ci может быть вычислена, как функция начальных данных.

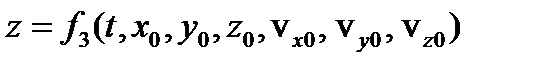
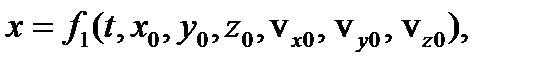


 ДУ с разделяющимися переменными
ДУ с разделяющимися переменными

 Чтобы решить задачу Коши, необходимо определить постоянную С по НУ
Чтобы решить задачу Коши, необходимо определить постоянную С по НУ

 ДУ прямолинейного движения точки имеет вид
ДУ прямолинейного движения точки имеет вид
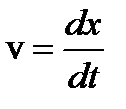
 Задача Коши решается последовательным их интегрированием
Задача Коши решается последовательным их интегрированием




 Выберем начало координат в положении статического равновесия пружины
Выберем начало координат в положении статического равновесия пружины
 ДУ свободных затухающих колебаний
ДУ свободных затухающих колебаний 






 х 1 – общее решение однородного уравнения
х 1 – общее решение однородного уравнения



 Силы инерции равна
Силы инерции равна

 Пусть сила тяжести
Пусть сила тяжести


 Главный вектор всех внутренних сил равен нулю
Главный вектор всех внутренних сил равен нулю
 точки равен нулю
точки равен нулю Важнейшей динамической характеристикой материальной точки, определяющей ее способность сохранять движение, является масса
Важнейшей динамической характеристикой материальной точки, определяющей ее способность сохранять движение, является масса точек с массой mi, то можно ввести массу всей системы, равную сумме масс ее точек
точек с массой mi, то можно ввести массу всей системы, равную сумме масс ее точек
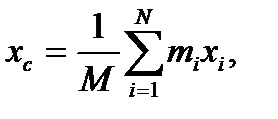

 Координаты ЦМ твердого тела
Координаты ЦМ твердого тела Если плотность распределения массы равна, то
Если плотность распределения массы равна, то

 Координаты центра масс равны
Координаты центра масс равны




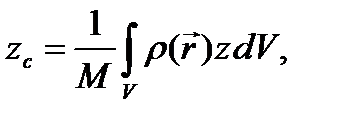

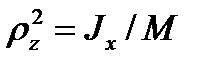
 инерции всего тела (системы)
инерции всего тела (системы) Теорема Гюйгенса
Теорема Гюйгенса
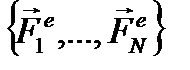 Пусть дана механическая система, состоящая из N взаимодействующих точек,на которую действуют внешние силы
Пусть дана механическая система, состоящая из N взаимодействующих точек,на которую действуют внешние силы Равнодействующую всех внутренних сил, действующих на k- ю точку со стороны других точек, обозначим так:
Равнодействующую всех внутренних сил, действующих на k- ю точку со стороны других точек, обозначим так: Тогда для каждой k- ойточки системы в инерциальной системе координат Oxyz уравнение движение имеет вид
Тогда для каждой k- ойточки системы в инерциальной системе координат Oxyz уравнение движение имеет вид


 Уравнения движения системы имеют вид
Уравнения движения системы имеют вид Чтобы найти закон движения ЦМ системы, просуммируем эти уравнения
Чтобы найти закон движения ЦМ системы, просуммируем эти уравнения


 Центр масс системы движется как материальная точка, масса которой равна массе всей системы и к которой приложены все внешние силы, действующие на систему
Центр масс системы движется как материальная точка, масса которой равна массе всей системы и к которой приложены все внешние силы, действующие на систему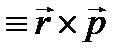
 Если в начальный момент времени ЦМ покоился, то он останется в покое и в дальнейшем. Если сумма проекций внешних сил на какую-нибудь ось (например ось x) равна нулю, то вдоль этой оси ЦМС движется равномерно и прямолинейно или покоится, если он покоился в начальный момент времени
Если в начальный момент времени ЦМ покоился, то он останется в покое и в дальнейшем. Если сумма проекций внешних сил на какую-нибудь ось (например ось x) равна нулю, то вдоль этой оси ЦМС движется равномерно и прямолинейно или покоится, если он покоился в начальный момент времени Важнейшим следствие данной теоремы является закон сохранения импульса
Важнейшим следствие данной теоремы является закон сохранения импульса Если главный вектор внешних сил, действующих на систему, равен нулю, то ее импульс сохраняется
Если главный вектор внешних сил, действующих на систему, равен нулю, то ее импульс сохраняется

 Если проекция главного вектора внешних сил, действующих на систему, на некоторую ось равна нулю, то проекция импульса системы на эту ось также сохраняется
Если проекция главного вектора внешних сил, действующих на систему, на некоторую ось равна нулю, то проекция импульса системы на эту ось также сохраняется
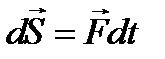 Элементарным импульсом силы называется вектор, равный произведению силы на элементарный промежуток времени
Элементарным импульсом силы называется вектор, равный произведению силы на элементарный промежуток времени Импульсом силы за конечный промежуток времени
Импульсом силы за конечный промежуток времени
 с помощью понятия импульса силы может быть представлена в интегральном виде
с помощью понятия импульса силы может быть представлена в интегральном виде

 Изменение импульса механической системы за некоторый промежуток времени равно главному вектору импульсов всех внешних сил, действующих на систему в этот промежуток времени
Изменение импульса механической системы за некоторый промежуток времени равно главному вектору импульсов всех внешних сил, действующих на систему в этот промежуток времени





 Если при движении точки момент действующей на нее
Если при движении точки момент действующей на нее импульса сохраняется
импульса сохраняется того же центра
того же центра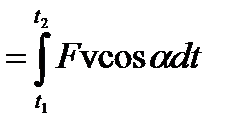




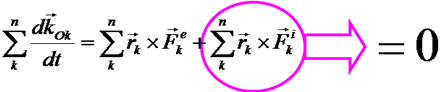



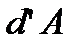



 от координат материальной точки, такая, что
от координат материальной точки, такая, что Вектор потенциальной силы определяется выражением
Вектор потенциальной силы определяется выражением Кинетическая энергия материальной точки i, равна половине произведения массы точки на квадрат ее скорости
Кинетическая энергия материальной точки i, равна половине произведения массы точки на квадрат ее скорости Кинетическая энергия аддитивна, поэтому кинетическая энергия системы n материальных точек определяется суммой
Кинетическая энергия аддитивна, поэтому кинетическая энергия системы n материальных точек определяется суммой
 Кинетическая энергия материальной точки i, складывается из кинетической энергии ее центра масс, в котором сосредоточена вся масса системы, и кинетической энергии движения системы относительно центра масс
Кинетическая энергия материальной точки i, складывается из кинетической энергии ее центра масс, в котором сосредоточена вся масса системы, и кинетической энергии движения системы относительно центра масс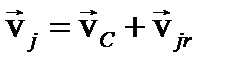 Д-во: Скорость любой точки i можно представить, как движение вместе c центром масс и относительно центра масс
Д-во: Скорость любой точки i можно представить, как движение вместе c центром масс и относительно центра масс
 Теорема об изменении кинетической энергии точки
Теорема об изменении кинетической энергии точки Остается, однако, не ясной связь между работой силы, приложенной к точке, и изменением ее скорости
Остается, однако, не ясной связь между работой силы, приложенной к точке, и изменением ее скорости