Обмен данными между MATLAB и Excel

Запустите Excel, проверьте, что проделаны все необходимые настройки так, как описано в предыдущем разделе (MATLAB должен быть закрыт). Введите в ячейки с A1 по C3 матрицу, для отделения десятичных знаков используйте точку в соответствии с требованиями Excel.

Рисунок 2 Пример ввода дробных чисел в Excel

Выделите на листе данные ячейки и нажмите кнопку putmatrix, появляется окно Excel с предупреждением о том, что MATLAB не запущен. Нажмите OK, дождитесь открытия MATLAB. Появляется диалоговое окно Excel со строкой ввода, предназначенной для определения имени переменной рабочей среды MATLAB, в которую следует экспортировать данные из выделенных ячеек Excel. Введите, к примеру, М и закройте окно при помощи кнопки OK. Перейдите к командному окну MATLAB и убедитесь, что в рабочей среде создалась переменная М, содержащая массив три на три:

Рисунок 3 Отображение массива М в командном окне.

Проделайте некоторые операции в MATLAB с матрицей М, например, обратите ее.

Вызов inv для обращения матрицы, как и любой другой команды MATLAB можно осуществить прямо из Excel. Нажатие на кнопку evalstring, расположенную на панели Excel Link, приводит к появлению диалогового окна, в строке ввода которого следует набрать команду MATLAB:

IM=inv(M)

Результат аналогичен полученному при выполнении команды в среде MATLAB.

Вернитесь в Excel, сделайте текущей ячейку A5 и нажмите кнопку getmatrix. Появляется диалоговое окно со строкой ввода, в которой требуется ввести имя переменной, импортируемой в Excel. В данном случае такой переменной является IM. Нажмите OK, в ячейки с A5 по A7 введены элементы обратной матрицы.

Итак, для экспорта матрицы в MATLAB следует выделить подходящие ячейки листа Excel, а для импорта достаточно указать одну ячейку, которая будет являться верхним левым элементом импортируемого массива. Остальные элементы запишутся в ячейки листа согласно размерам массива, переписывая содержащиеся в них данные, поэтому следует соблюдать осторожность при импорте массивов.

Вышеописанный подход является самым простым способом обмена информацией между приложениями — исходные данные содержатся в Excel, затем экспортируются в MATLAB, обрабатываются там некоторым образом и результат импортируется в Excel. Пользователь переносит данные при помощи кнопок панели инструментов Excel Link. Информация может быть представлена в виде матрицы, т.е. прямоугольной области рабочего листа. Ячейки, расположенные в строку или столбец, экспортируются, соответственно, в вектор-строки и вектор-столбцы MATLAB. Аналогично происходит и импорт вектор-строк и вектор-столбцов в Excel.

Программирование

 

М-файлы

Работа из командной строки MATLAB затрудняется, если требуется вводить много команд и часто их изменять. Ведение дневника при помощи команды diary и сохранение рабочей среды незначительно облегчают работу. Самым удобным способом выполнения групп команд MATLAB является использование М-файлов, в которых можно набирать команды, выполнять их все сразу или частями, сохранять в файле и использовать в дальнейшем. Для работы с М-файлами предназначен редактор М-файлов. С его помощью можно создавать собственные функции и вызывать их, в том числе и из командного окна.

Откройте меню File основного окна MATLAB и в пункте New выберите подпункт M-file. Новый файл открывается в окне редактора M-файлов, которое изображено на рисунке 4.

Рисунок 4. Окнo редактора M-файлов

М-файлы в MATLAB бывают двух типов: файл-программы (Script M-Files), содержащие последовательность команд, и файл-функции, (Function M-Files), в которых описываются функции, определяемые пользователем.

Файл-программа

Наберите в редакторе команды, приводящие к построению двух графиков на одном графическом окне

Рисунок 5 Команды файла в окне редактора.

Сохраните теперь файл с именем mydemo.m в подкаталоге work основного каталога MATLAB, выбрав пункт Save as меню File редактора. Для запуска на выполнение всех команд, содержащихся в файле, следует выбрать пункт Run в меню Debug. На экране появится графическое окно Figure 1, содержащее графики функций.

Команды файл-программы осуществляют вывод в командное окно. Для подавления вывода следует завершать команды точкой с запятой. Если при наборе сделана ошибка и MATLAB не может распознать команду, то происходит выполнение команд до неправильно введенной команды, после чего выводится сообщение об ошибке в командное окно.

Очень удобной возможностью, предоставляемой редактором М-файлов, является выполнение части команд. Закройте графическое окно Figure 1. Выделите при помощи мыши, удерживая левую кнопку, или клавишами со стрелками при нажатой клавише Shift, первые четыре команды и выполните их из пункта Text. Обратите внимание, что в графическое окно вывелся только один график, соответствующий выполненным: командам. Запомните, что для выполнения части команд их следует выделить и нажать клавишу F9.

Отдельные блоки М-файла можно снабжать комментариями, которые пропускаются при выполнении, но удобны при работе с М-файлом. Комментарии начинаются со знака процента и автоматически выделяются зеленым цветом, например:

Рисунок 6 Команды файла с комментариями.

Открытие существующего М-файла производится при помощи пункта Open меню File рабочей среды, либо редактора М-файлов.

Файл-функция

Рассмотренная выше файл-программа является только последовательностью команд MATLAB, она не имеет входных и выходных аргументов. Для использования численных методов и при программировании собственных приложений в MATLAB необходимо уметь составлять файл-функции, которые производят необходимые действия с входными аргументами и возвращают результат действия в выходных аргументах. Разберем несколько простых примеров, позволяющих понять работу с файл-функциями.

Для проведения предобработки данных многомерного анализа часто используют операцию центрирования. Имеет смысл один раз написать файл-функцию, а потом вызывать его всюду, где необходимо производить центрирование. Откройте в редакторе М-файлов новый файл и наберите

Рисунок 7 Пример файла – функции.

Слово function в первой строке определяет, что данный файл содержит файл-функцию. Первая строка является заголовком функции, в которой размещается имя функции и списка входных и выходных аргументов. В примере имя функции centering, один входной аргумент X и один выходной — Xc. После заголовка следуют комментарии, а затем — тело функции (оно в данном примере состоит из двух строк), где и вычисляется ее значение. Важно, что вычисленное значение записывается в Xc. Не забудьте поставить точку с запятой для предотвращения вывода лишней информации на экран. Теперь сохраните файл в рабочем каталоге. Обратите внимание, что выбор пункта Save или Save as меню File приводит к появлению диалогового окна сохранения файла, в поле File name которого уже содержится название centering. Не изменяйте его, сохраните файл функцию в файле с предложенным именем!

Теперь созданную функцию можно использовать так же, как и встроенные sin, cos и другие. Вызов собственных функций может осуществляться из файл-программы либо из другой файл-функции. Попробуйте сами написать файл-функцию, которая будет шкалировать матрицы, т.е. делить каждый столбец на величину среднеквадратичного отклонения по этому столбцу.

Можно написать файл-функции с несколькими входными аргументами, которые размещаются в списке через запятую. Можно также создавать и функции, возвращающие несколько значений. Для этого выходные аргументы добавляются через запятую в список выходных аргументов, а сам список заключается в квадратные скобки. Хорошим примером является функция, переводящая время, заданное в секундах, в часы, минуты и секунды.

Рисунок 8 Команды функции перевода времени.

При вызове файл-функций с несколькими выходными аргументами результат следует записывать в вектор соответствующей длины.

Создание графика

MATLAB имеет широкие возможности для графического изображения векторов и матриц, а также для создания комментариев и печати графиков. Приведем описание несколько важных графических функций.

Функция plot имеет различные формы, связанные с входными параметрами, например plot(y) создает кусочно-линейный график зависимости элементов y от их индексов. Если в качестве аргументов заданы два вектора, то plot(x,y) создаст график зависимости y от x.

Рисунок 9 Пример команд для построения графика функции sin в интервале от 0 до 2p

Программа построила график зависимости, который отображается в окне Figure 1

Рисунок 10 График функции sin в интервале от 0 до 2p

MATLAB автоматически присваивает каждому графику свой цвет (исключая случаи, когда это делает пользователь), что позволяет различать наборы данных.

Команда hold on позволяет добавлять кривые на существующий график. Функция subplot позволяет выводить множество графиков в одном окне

Рисунок 11. Пример использования функции subplot.

Рисунок 12. Результат использования функции subplot.

 

Печать графиков

Пункт Print в меню File и команда print печатают графику MATLAB. Меню Print вызывает диалоговое окно, которое позволяет выбирать общие стандартные варианты печати. Команда print обеспечивает большую гибкость при выводе выходных данных и позволяет контролировать печать из М-файлов. Результат может быть послан прямо на принтер, выбранный по умолчанию, или сохранен в заданном файле.

 

Лабораторная работа № 1

 

Цель работы: освоить операции матричного вычисления средствами универсальной системы MATLAB.

Порядок выполнения работы

Средствами универсальной системы MATLAB получить для исходной матрицы А размерности (3х4) следующие величины:

 

- транспонированную, псевдообратную, евклидову норму;

- собственные значения и собственные векторы;

- сингулярные числа, правые и левые сингулярные векторы.

Оформление отчета

Отчетом о лабораторной работе является файл с именем, совпадающим с фамилией студента с результатами работы в папке Мои документы/номер группы.

1.5.3. Контрольные вопросы

1. Что такое иммунокомпьютинг?

2. Перечислите основные вычислительные процедуры иммунокомпьютинга.

3. Свойства сингулярного разложения матриц.

4.

5.

6.

7.

8.

9.

10.

 

 

2. ВЫЧИСЛИТЕЛЬНАЯ ПРОЦЕДУРА СИНГУЛЯРНОГО РАЗЛОЖЕНИЯ МАТРИЦ

Математический аппарат

 

Как известно, для произвольной матрицы А размерности (m´ n) существует так называемое сингулярное разложение, т.е. представление матрицы в виде

A = USVT,

(1)

где U ‑ (m ´ m) и V – (n x n) – ортогональные квадратные матрицы, удовлетворяющие критерию ортогональности:

 

VV^T = V^TV = E_m´m, UU^T = U^T U = E_n´n,

где E ‑ единичные матрицы соответствующих размерностей.

Матрица S состоит из квадратного диагонального блока размерности r´r (r = min (m, n)) с неотрицательными элементами на главной диагонали и, если , из дополнительных нулевых строк или столбцов

 

S = [S^’;0], если m < n,

S = [S^’;0]^T, если m > n,

S = S^’, если m = n,

S^’= diag {s₁,s₂,…,s_r, s₁ s₂ … s_r}.

Числа s_i, i = 1, 2,….,r называются сингулярными числами матрицы A, которые определяются матрицей A однозначно.

Сингулярное разложение вещественной прямоугольной матрицы A в покомпонентной форме имеет следующеепредставление:

 

A= s₁U₁V₁^T + s₂U₂V₂^T + …. +s_rU_rV_r^T, (2)

 

где s_i –сингулярные числа матрицы A, U_i, V_i – соответственно, правые и левые сингулярные векторы, r –ранг матрицы. Эти сингулярные числа и сингулярные векторы удовлетворяют следующим соотношениям:

 

s₁ ³ s₂ ³…,s_r ³ 0, s_i = U_i^T AV_i, U_i^TU_i = 1, V_i^T V_i = 1,

i = 1,….,r. (3)

 

Известно, что процессы сингулярного разложения для любой вещественной матрицы А обладают весьма полезными свойствами для теории и приложений, а именно, каждая матрица над полем вещественных чисел имеет вещественные сингулярные числа и векторы. Кроме того, сингулярное разложение матриц устойчиво к малым возмущениям матриц, т.е. сингулярное разложение каждой матрицы является хорошо обусловленной процедурой.

Относительно практических аспектов, сингулярное разложение матрицы в общем случае может быть получено по достаточно простой и надежной схеме:

 

V^T_(k+1) = U^T_(k)A, V_(k+1) = V_(k+1)/ /V_(k+1)/

U_{(k+1) =} AV_(k+1), U_(k+1) = U_(k+1)/ /U_(k+1)/ (4)

s_k = U^T_kAV_k, /s_k+1 – s_k/ ≤ ε

 

где k=0,1,2,... – номер итерации, |U_(k+1)| - любая векторная норма, e - заданная точность вычисления. Можно показать, что для произвольных начальных векторов U₍₀₎, V₍₀₎ итерации по схеме (4) сходятся в общем случае к сингулярным векторам U, V, соответствующим максимальному сингулярному числу s_max= U^TAV.

Следуют отметить, что такие свойства не свойственны спектральному разложению, которое в действительности формирует основу для многомерного статистического анализа. В отличие от сингулярного разложения матриц, собственные числа и собственные векторы спектрального разложения являются вещественными только для вещественных симметрических матриц, в общем случае не симметрические вещественные матрицы обладают комплексным спектром и определить его не просто.

С использованием вышеприведенного итеративного алгоритма (4) сингулярное разложение матрицы А, представленное в форме (2,3) может быть получено с использованием метода исчерпывания.

Сущность этого метода заключается в следующем:

· максимальное сингулярное число и соответствующие ему правый и левый сингулярный векторы матрицы А вычисляются с помощью итеративного алгоритма (4). Формируется матричная компонента А₁ =s₁U₁V^T₁;

· формируется матрица невязки

 

А₂ = А ‑ А₁ = А ‑ s₁U₁V^T₁, (5)

для которой максимальное сингулярное число и соответствующие ему правый и левый сингулярный векторы матрицы А₂ вычисляются с помощью итеративного алгоритма (4) и т.д.

 

Лабораторная работа № 2

Цель работы: создание программного модуля для сингулярного разложения произвольной матрицы.

 

Порядок выполнения работы

 

1. Открыть универсальную систему MATLAB.

2. Задать исходную матрицу А размерности (4 х 3).

3. Используя команду для сингулярного разложения MATLAB, получить представление для матрицы А через сингулярные числа, правые и левые сингулярные векторы в покомпонентной (в виде 2, 3) и в векторно-матричной формах (в виде 1).

4. Проверить условия ортогональности для вышеперечисленных форм представления.

5. Реализовать итеративную процедуру (4) вычисления максимального сингулярного числа и соответствующих ему правого и левого сингулярных векторов при произвольно заданных начальных значениях левого сингулярного вектора U₀ и правого сингулярного вектора V₀. Вычислить матричную компоненту, соответствующую найденным максимальному сингулярному числу и соответствующим ему правому и левому сингулярным векторам.

6. Используя процедуру метода исчерпывания, получить матричную невязку вида (5), для которой выполнить все перечисленные операции пункта 4.

7. Сохранить все результаты выполнения работы в файле на диске.

Пример выполнения лабораторной работы №2

 

В соответствии с п.2 формируем произвольную матрицу А размерности (3×4)с помощью генератора случайных чисел: A=rand(3,4), проверяемусловия ортогональности: U*U^T, V*V^T:

Рисунок 13

 

Получаем представление в покомпонентной форме:

- для первого слагаемого в (2) формируем следующие компоненты сингулярного разложения: первый левый сингулярный вектор ‑ U1=U(:,1), первое сингулярное число ‑ S1=S(1,1), первый правый сингулярный вектор ‑ V1=V(:,1), с использованием полученных компонент формируем первое слагаемое в (2): S1*U1*V1T;

- аналогично формируем компоненты сингулярного разложения для второго слагаемого: U2=U(:,2), S2=S(2,2), V2=V(:,2). Вычисляем второе слагаемое S2*U2*V2T и т.д.

 

Рисунок 14

 

В соответствии с п.4 для реализации интеративной процедуры вычисления максимального сингулярного числа и соответствующих правого и левого сингулярных векторов задаем исходные данные: матрицу А размерности (3×4), произвольные: левый сингулярный вектор U0 размерности (3×1), правый сингулярный вектор V0 размерности (4×1), число, характеризующее точность вычисления epsilon = 0.01. По заданным исходным данным вычисляем значение сингулярного числа S0=U0^T*A*V0. Итеративный алгоритмвключает следующие шаги:

 

Шаг 1. V1^T=U0^T*A, V1/norm(V1) – вычисление правого сингулярного вектора и его нормировка;

U1=A*V1, U1=U1/norm(U1)‑ вычисление левого сингулярного вектора и его нормировка;

S1=U1^T*A*V1 – вычисление сингулярного числа;

/S1- S0/≤epsilon=0.01 – проверка точности определения сингулярного числа, если условие выполняется, то вычисленные компоненты запоминаются, как первые компоненты сингулярного разложения, в противном случае переходим к шагу 2.

 

Шаг 2. V2^T=U1^T*A, V2/norm(V2) – вычисление правого сингулярного вектора и его нормировка;

U2=A*V2, U2=U2/norm(U1)‑ вычисление левого сингулярного вектора и его нормировка;

S2=U2^T*A*V2 – вычисление сингулярного числа;

/S2- S1/≤epsilon=0.01 – проверка точности вычисления сингулярного числа и т.д.

 

Рисунок 15

После первой итерации модуль разности двух последующих сингулярных чисел не удовлетворяет заданной точности вычисления, поэтому необходимо следующие шаги до тех пор, пока неравенство не будет удовлетворено.

 

2.2.3. Порядок оформления отчета

Отчетом о лабораторной работе №2 является файл с именем, совпадающим с фамилией студента с результатами работы в папке Мои документы/номер группы.

2.2.4. Контрольные вопросы

1. Свойство сходимости вычислительной процедуры (4).

2. Преимущество сингулярного разложения матриц перед спектральным разложением матриц.

3. Условие останова итеративного алгоритма вычисления максимального сингулярного числа, правого и левого сингулярного вектора.

4. В чем заключается сущность метода исчерпывания?

5.

6.

7.

8.

9.

10.

3. ВЫЧИСЛИТЕЛЬНАЯ ПРОЦЕДУРА ОБУЧЕНИЯ С ЭКСПЕРТОМ

Математический аппарат

Пусть имеется сложная система (научная, техническая, экономическая и т.д.), которая может характеризоваться определенным набором признаков X_k, k = 1,2,3,…. Такой произвольный вектор значений признаков можно трактовать как образ, принадлежащий пространству признаков {X}.

Множество образов представляется в виде множества векторов, состоящего из k подмножеств или классов:

z₁={X}₁,..., z_k={X}_k.

Для процедуры обучения с экспертом исходной информацией служат векторы значений признаков ситуаций по каждому из рассматриваемых эталонных классов и сформированная на основе мнения эксперта обучающая выборка. Исследуя и анализируя указанным образом, ряд таких систем с привлечением эксперта-человека, можно на основании его знаний и личного опыта выстроить классификацию и оценить, к какому из классов принадлежит исследуемый объект. Набор признаков системы, перечисленный выше, эксперт может оценивать либо по 10-бальной системе, либо в пределах от 0 до 1, как в рассматриваемом ниже примере.

На основе полученной информации и с учетом мнения эксперта формируется обучающая выборка, которая представлена в таблице 1.

Таблица 1. Обучающая выборка

Номер объекта	Значения признаков	Классификация эксперта
z1	z 2	z3		zn
		0,3
	0,1	0,6
	0,2	0,8	0,9		0,7
	0,5		0,7		0,1
:
L			0,5		0,1

 

Задача обучения сводится к разбиению пространства признаков на классы (т.е. к проведению классификации), а задача распознавания сводится к определению класса z_j ={X}_j, j=1,...,k, с помощью векторной нормы:

 

z_k(X): min_k // X - {X}_k //.

 

В качестве векторной нормы могут быть использованы следующие известные нормы:

 

· евклидова норма // X_i – X_ki//_Е = (Σ_i(X_i – X_ki)²)^1/2;

· норма расстояния // X_i – X_ki//_М = (Σ_i/X_i – X_ki/);

· норма Чебышева // X_i – X_ki//_С = max_i/X_i – X_ki/.

В вычислительных процедурах иммунокомпьютинга в качестве аналога расстояния используется понятие энергии связи, основанное на сингулярном разложении матрицы. Энергия связи между объектами A и M представляется следующим образом:

 

ω_i = - U ^Т_i MV_i, U_i^TU_i = 1, V_i^T V_i = 1, i =1,,r,

 

где U_i, V_i – соответственно, правые и левые сингулярные векторы

матрицы А, r –ранг матрицы.

Алгоритм вычислительной процедуры обучения с экспертом состоит их следующих шагов:

Шаг 1. Сворачивание вектора в матрицу. Заданный вектор Х размерности (n x 1) сворачиваем в матрицу M размерности n_U x n_V = n.

Шаг 2. Формируем матрицы A₁, A₂,….,A_k дляэталонных классов с = 1,…,к и вычисляем их сингулярные векторы:

 

{U₁, V₁} – для A₁, {U₂, V₂} - для A₂, {U_к, V_к} - для A_k.

Шаг 3. Распознавание. Для каждого входного образа М вычисляем к значений энергии связи между каждой парой сингулярных векторов:

ω₁ = - U ^Т₁ MV₁, ….., ω_k = - U ^Т_к MV_к.

 

Шаг 4. Определяем класс, к которому принадлежит входной образ М. Минимальное значение энергии связи ω^* определяет этот класс,:

 

c = ω^* = min_c { ω_c }.

Лабораторная работа № 3

Цель работы: создание программного модуля для реализации вычислительной процедуры обучения с экспертом на основе инструментария универсальной системы MATLAB.

Порядок выполнения работы

1. Открыть универсальную систему MATLAB.

2. Задать обучающие матрицы А_i и матрицу М размерности (4 х 3).

3. Программно реализовать шаги 1-4 алгоритма вычислительной процедуры обучения с экспертом.

4. Сохранить все результаты выполнения работы в файле на диске.

3.2.2. Порядок оформления отчета

Отчетом о лабораторной работе № 3 является файл с именем, совпадающим с фамилией студента с результатами работы в папке Мои документы/номер группы.

 

Пример выполнения лабораторной работы №3

В соответствии с п. 2 формируем обучающие матрицы трех эталонных классов А_i,i=1,2,3 размерности (4 х 3)и анализируемую матрицу М размерности (4 х 3).

 

Рисунок 16 Обучающие матрицы трёх эталонных классов.

 

Для сформированных обучающих эталонных матриц А_i, i=1,2,3 вычисляем первые левые и правые сингулярные векторы U_i, V_i, i=1,2,3.

 

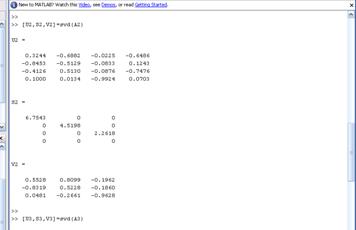
Рисунок 17

 

Используя эти компоненты, вычисляем значения энергии связи анализируемой матрицы М сэталонными обучающими матрицами А_i

 

Рисунок 18

 

Из вычисленных значений энергии связи формируем множество W=[W₁₁, W_21, W₃₁], минимальное значение которого определяет принадлежность анализируемого объекта к соответствующему классу.

Вывод: анализируемый объект относится к первому классу.

 

3.2.4. Контрольные вопросы

1. Что такое энергия связи?

2. Роль эксперта при реализации вычислительной процедуры обучения с экспертом.

3. Что является мерой близости выбранного образа М к конкретному классу?

4.

5.

6.

7.

8.

9.

10.

4. ВЫЧИСЛИТЕЛЬНАЯ ПРОЦЕДУРА ОБУЧЕНИЯ С ЭКСПЕРТОМ